 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
解が整数じゃなくても解けるよ
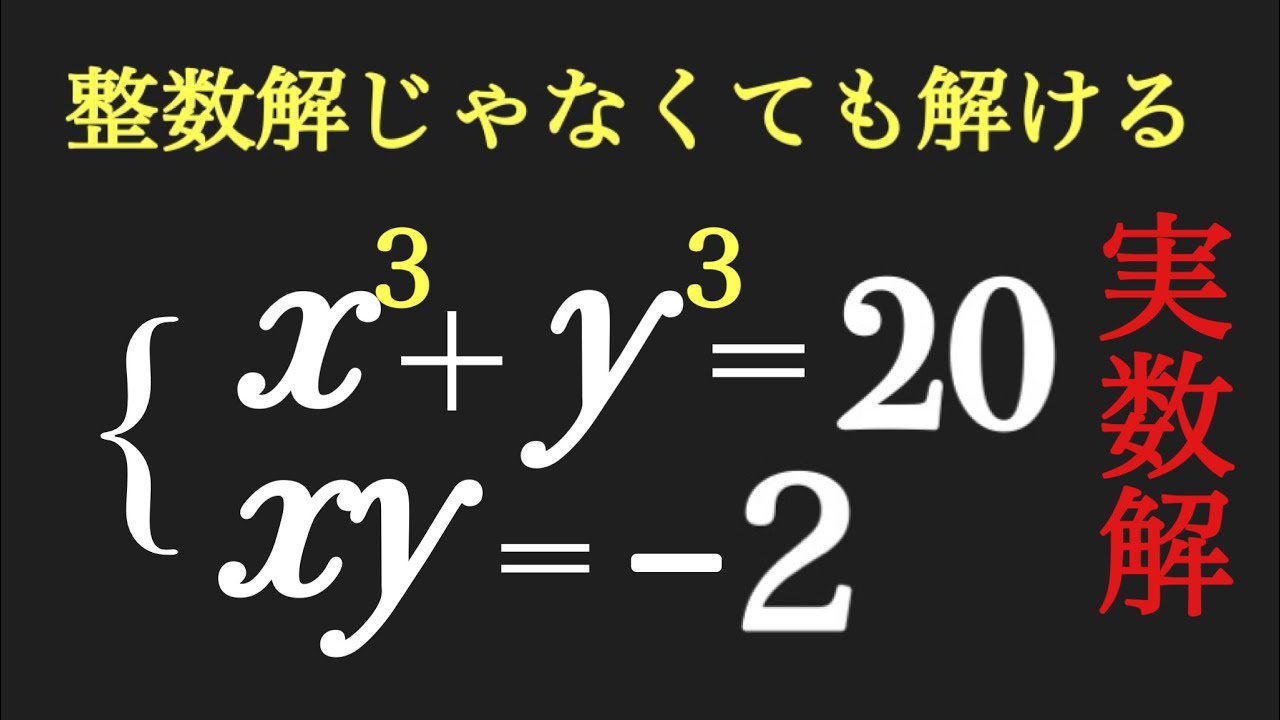
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3-91 \\
xy=12
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3=20 \\
xy=-2
\end{array}
\right.
\end{eqnarray}$
この動画を見る
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3-91 \\
xy=12
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3=20 \\
xy=-2
\end{array}
\right.
\end{eqnarray}$
お茶の水女子大 連立二元三次方程式
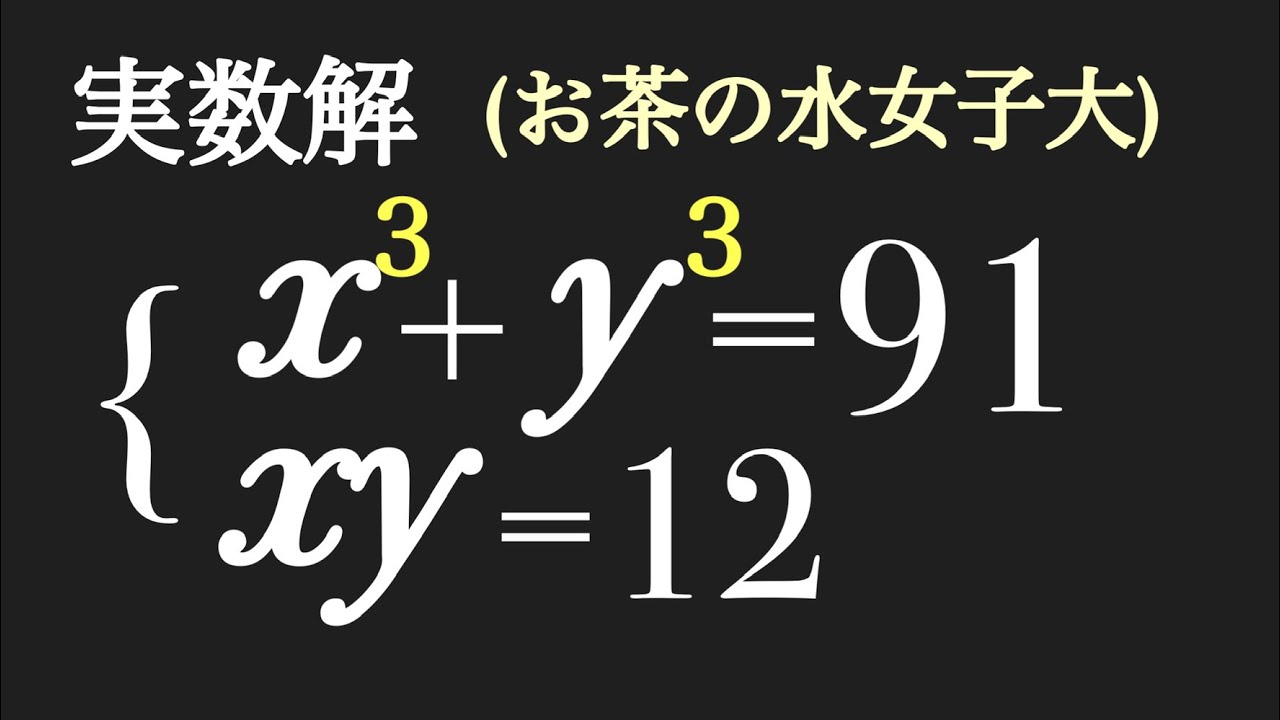
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3=91 \\
xy=12
\end{array}
\right.
\end{eqnarray}$
お茶の水女子大過去問
この動画を見る
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3=91 \\
xy=12
\end{array}
\right.
\end{eqnarray}$
お茶の水女子大過去問
ざ・因数分解

見掛け倒しの対数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\log_{\log_6(x-3)}81=4$
この動画を見る
これを解け.
$\log_{\log_6(x-3)}81=4$
息抜き問題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
これの和を求めよ.
$7+77+777+・・・・・・+\overbrace{77・・・・77}^{ n桁 }$
この動画を見る
これの和を求めよ.
$7+77+777+・・・・・・+\overbrace{77・・・・77}^{ n桁 }$
ガウス記号の入った二次方程式

何でもない不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$2^x+2^{\vert x\vert}\geqq 2\sqrt2$
この動画を見る
これを解け.
$2^x+2^{\vert x\vert}\geqq 2\sqrt2$
パスカルの三角形の証明・二項定理

あれを使うと超簡単!二項展開の応用 慶應・東大(1999,2015)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(a+b)^n$の係数がすべて奇数となる$n$がある.
(1)$n=1,3$
(2)$k$番目を$n$で表せ.
慶應・東大(1999,2015)過去問
この動画を見る
$(a+b)^n$の係数がすべて奇数となる$n$がある.
(1)$n=1,3$
(2)$k$番目を$n$で表せ.
慶應・東大(1999,2015)過去問
いい問題
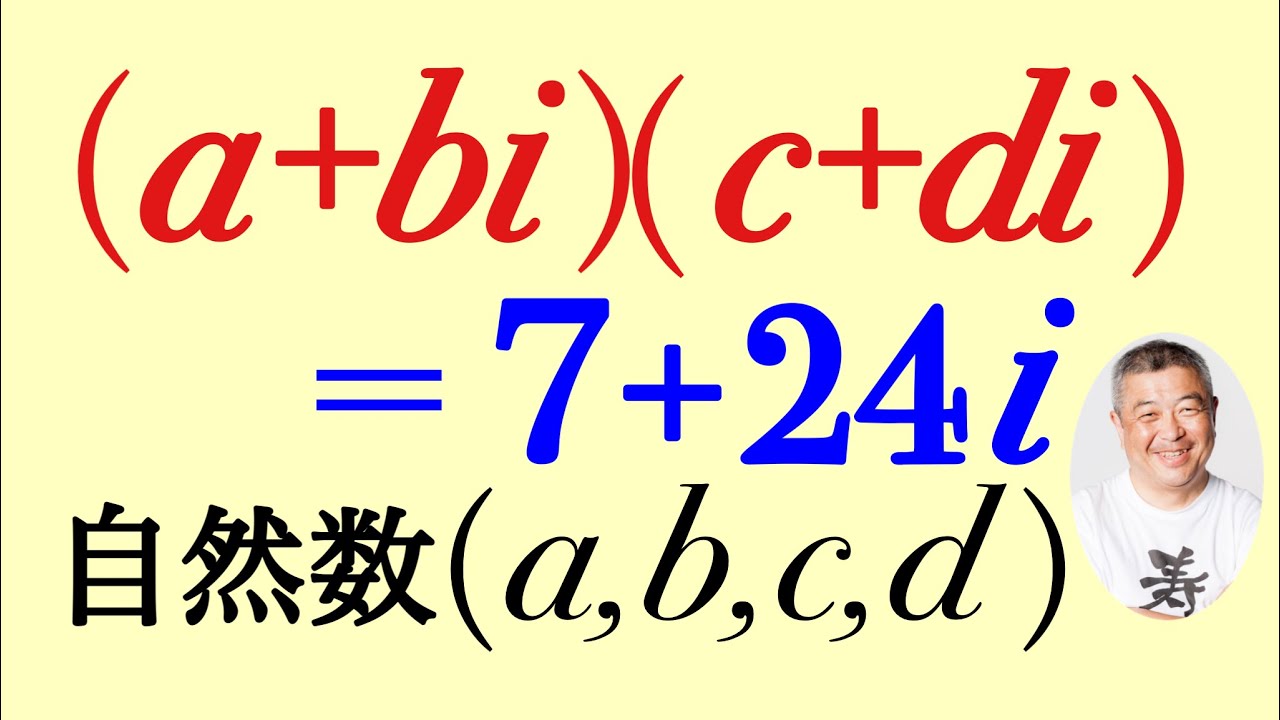
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$(a,b,c,d)$をすべて求めよ.
$(a+bi)(c+di)=7+24i$
この動画を見る
自然数$(a,b,c,d)$をすべて求めよ.
$(a+bi)(c+di)=7+24i$
無理数であることの証明

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x$が無理数なら$x^2,x^3$の少なくとも一方は無理数であることを示せ.
この動画を見る
$x$が無理数なら$x^2,x^3$の少なくとも一方は無理数であることを示せ.
不思議な方程式。優秀な視聴者様!疑問に答えて!
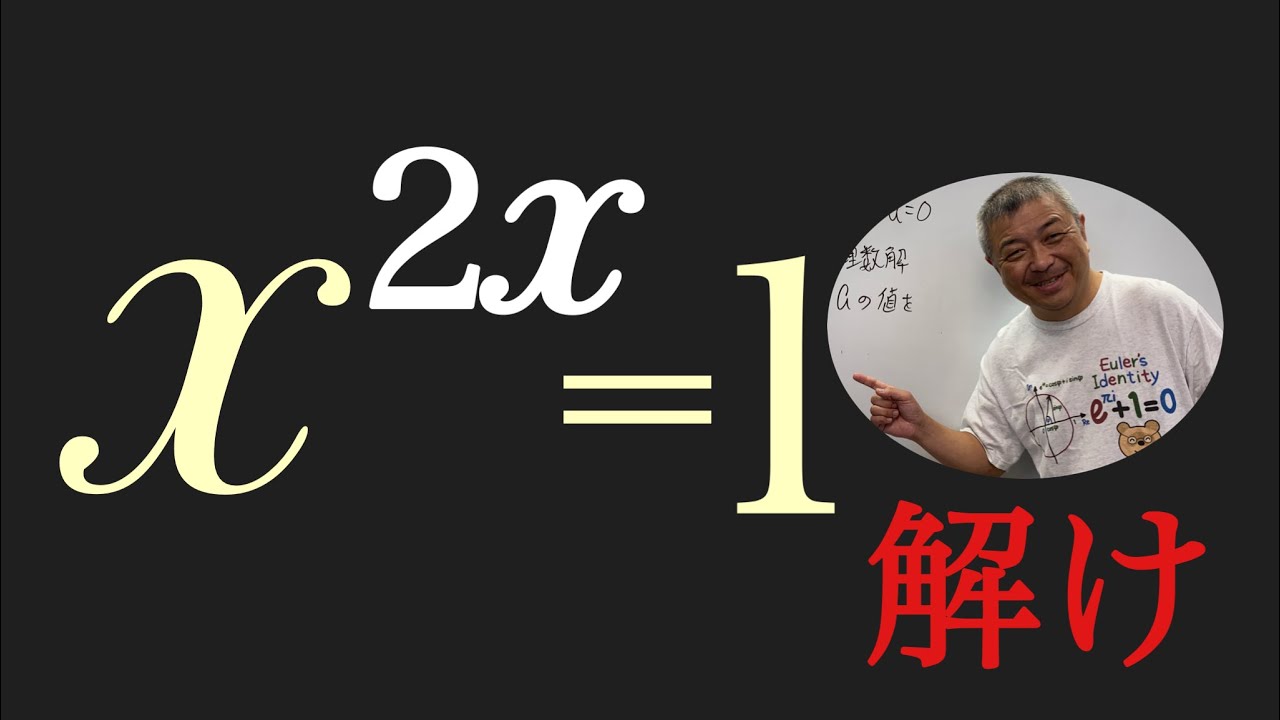
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x$は実数である.
$x^{2x}=1$
この動画を見る
これを解け.$x$は実数である.
$x^{2x}=1$
藤井聡太 三冠 竜王奪取の確率を計算する

連立方程式
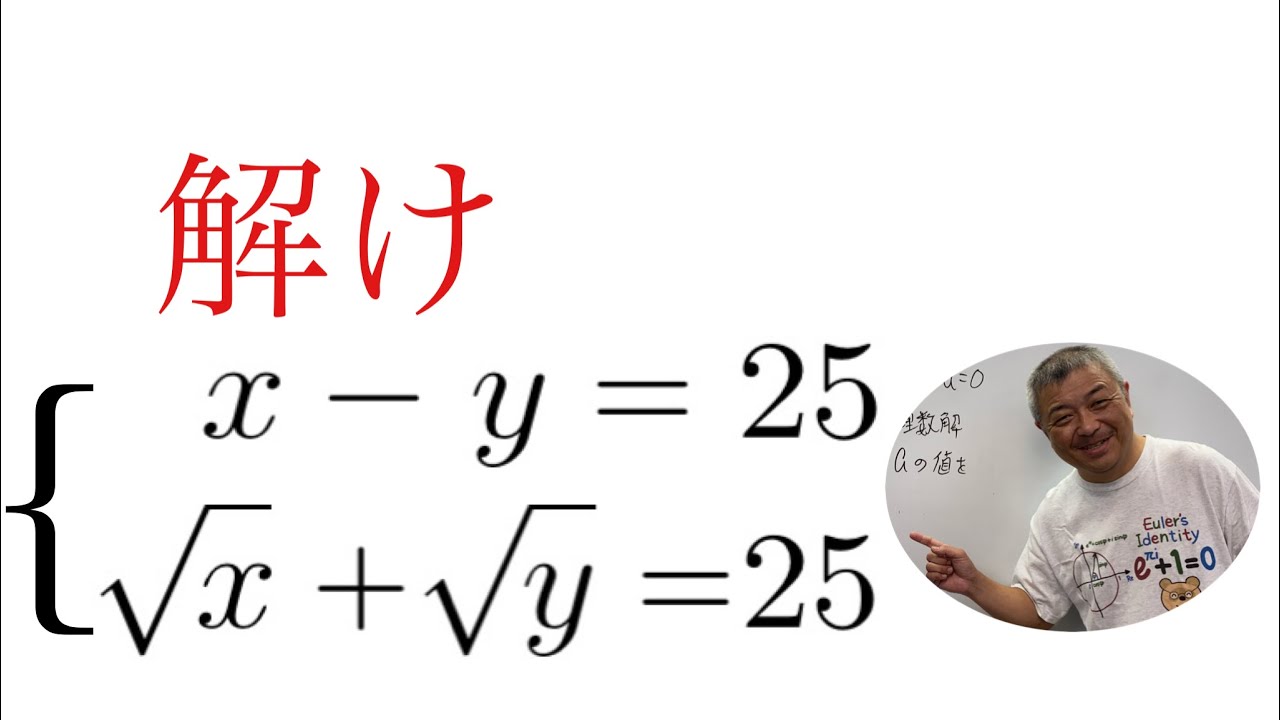
単元:
#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = 25 \\
\sqrt x + \sqrt y = 25
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = 25 \\
\sqrt x + \sqrt y = 25
\end{array}
\right.
\end{eqnarray}$
ウィルソンの定理

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$22!$を$23$で割った余りを求めよ.
$100!$を$101$で割った余りを求めよ.
この動画を見る
$22!$を$23$で割った余りを求めよ.
$100!$を$101$で割った余りを求めよ.
超簡単な方程式

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$ 0\leqq x\leqq 2\pi$
$25^{\cos x}-6・5^{\cos x-\frac{1}{2}}+1=0$
この動画を見る
これを解け.$ 0\leqq x\leqq 2\pi$
$25^{\cos x}-6・5^{\cos x-\frac{1}{2}}+1=0$
e^π>22 示せ
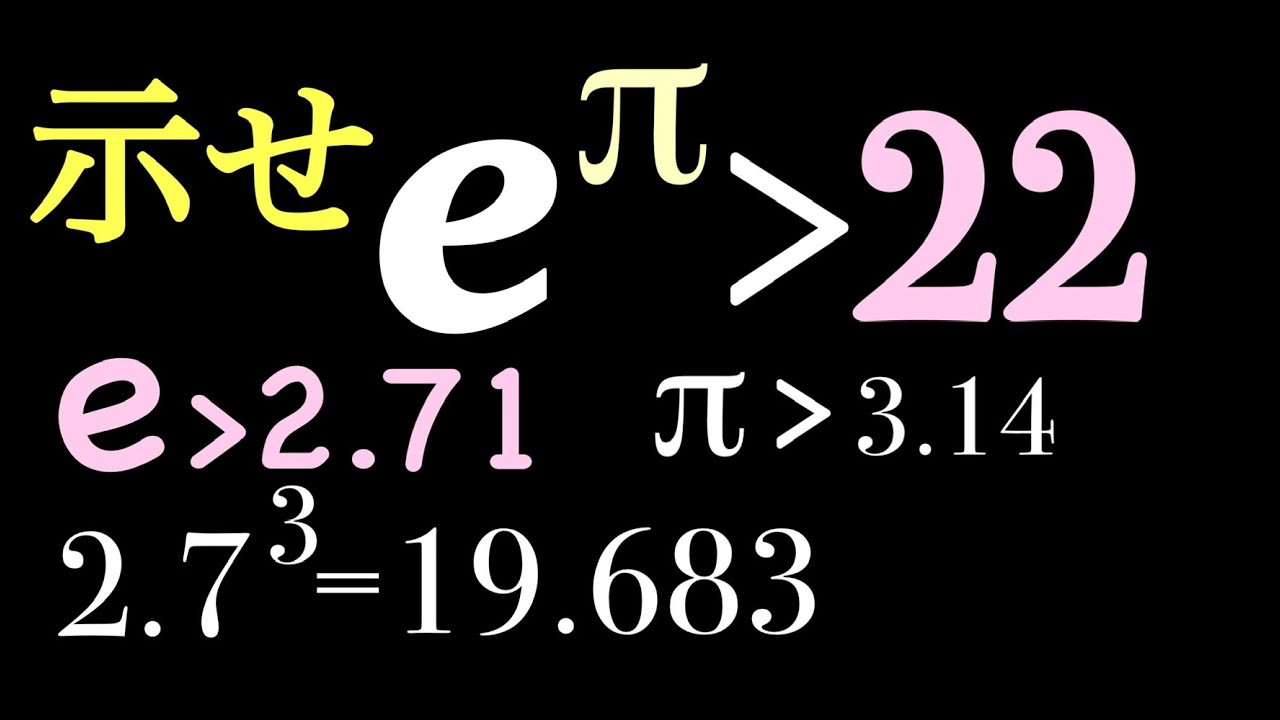
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$e^{\pi}\gt 22$を示せ.
$e \gt 2.71,\pi\gt 3.14$
この動画を見る
$e^{\pi}\gt 22$を示せ.
$e \gt 2.71,\pi\gt 3.14$
x^πを微分せよ

整数解をもつ2次方程式

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2+2(m+3)x-m-10=0$が整数解をもつような整数$m$を求めよ.
この動画を見る
$x^2+2(m+3)x-m-10=0$が整数解をもつような整数$m$を求めよ.
広島大2002漸化式 最大項を求める

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_{1}=-30$であり,$9a_{a+1}=a_n-\dfrac{4}{3^n}$である.
$a_n$が最大となる自然数$n$を求めよ.
広島大過去問
この動画を見る
$a_{1}=-30$であり,$9a_{a+1}=a_n-\dfrac{4}{3^n}$である.
$a_n$が最大となる自然数$n$を求めよ.
広島大過去問
整数問題
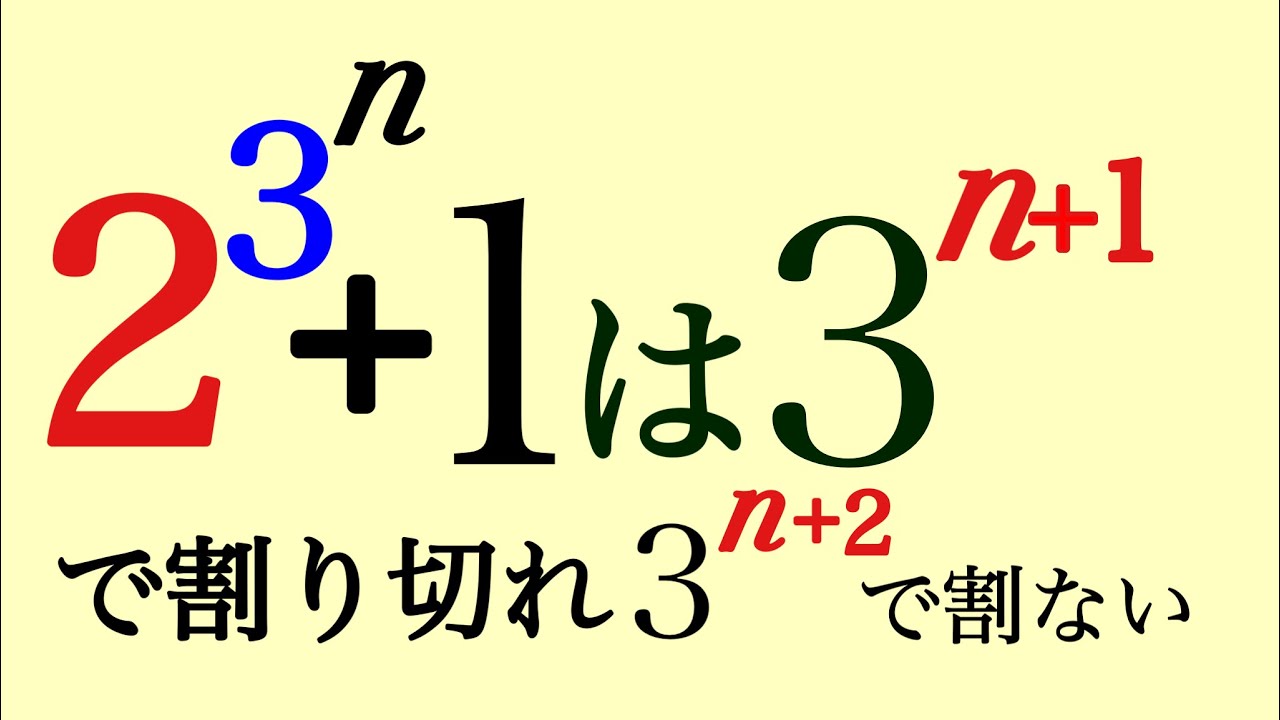
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数とする.
$2^{3^n}+1$は$3^{n+1}$で割り切れ,$3^{n+2}$では割り切れないことを示せ.
この動画を見る
$n$は自然数とする.
$2^{3^n}+1$は$3^{n+1}$で割り切れ,$3^{n+2}$では割り切れないことを示せ.
ちょっと複雑な漸化式

立教大 整式の剰余

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2002}$を$x^4-1$で割った余りを求めよ.
立教大過去問
この動画を見る
$x^{2002}$を$x^4-1$で割った余りを求めよ.
立教大過去問
3つの解法・漸化式
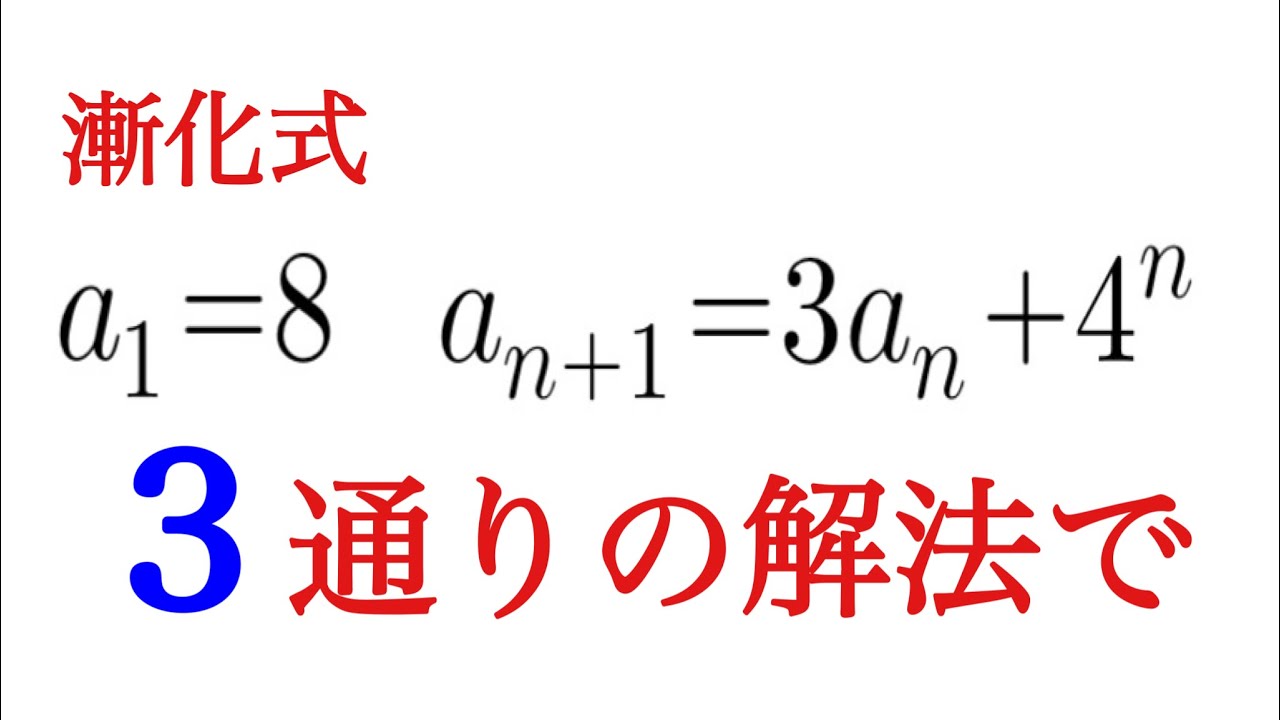
どっちがでかい?お願い⁉️気づいて

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$8^{3\sqrt9}$ vs $81$
この動画を見る
どちらが大きいか?
$8^{3\sqrt9}$ vs $81$
一発でできる!二重根号のはずし方

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
二重根号のはずし方に関して解説していきます.
この動画を見る
二重根号のはずし方に関して解説していきます.
頑張れば中学生にも解ける問題

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a=\sqrt{\dfrac{1!2!3!・・・・・・25!26!}{n}}$が自然数となる最小の自然数$n$である.
そのとき,$a$の末尾に$0$は何個並ぶか.
この動画を見る
$ a=\sqrt{\dfrac{1!2!3!・・・・・・25!26!}{n}}$が自然数となる最小の自然数$n$である.
そのとき,$a$の末尾に$0$は何個並ぶか.
もっちゃんと数学 フェルマーの小定理

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
フェルマーの定理に関して解説していきます.
この動画を見る
フェルマーの定理に関して解説していきます.
ガチャ問題 東大大島さんと数学

指数方程式だよ
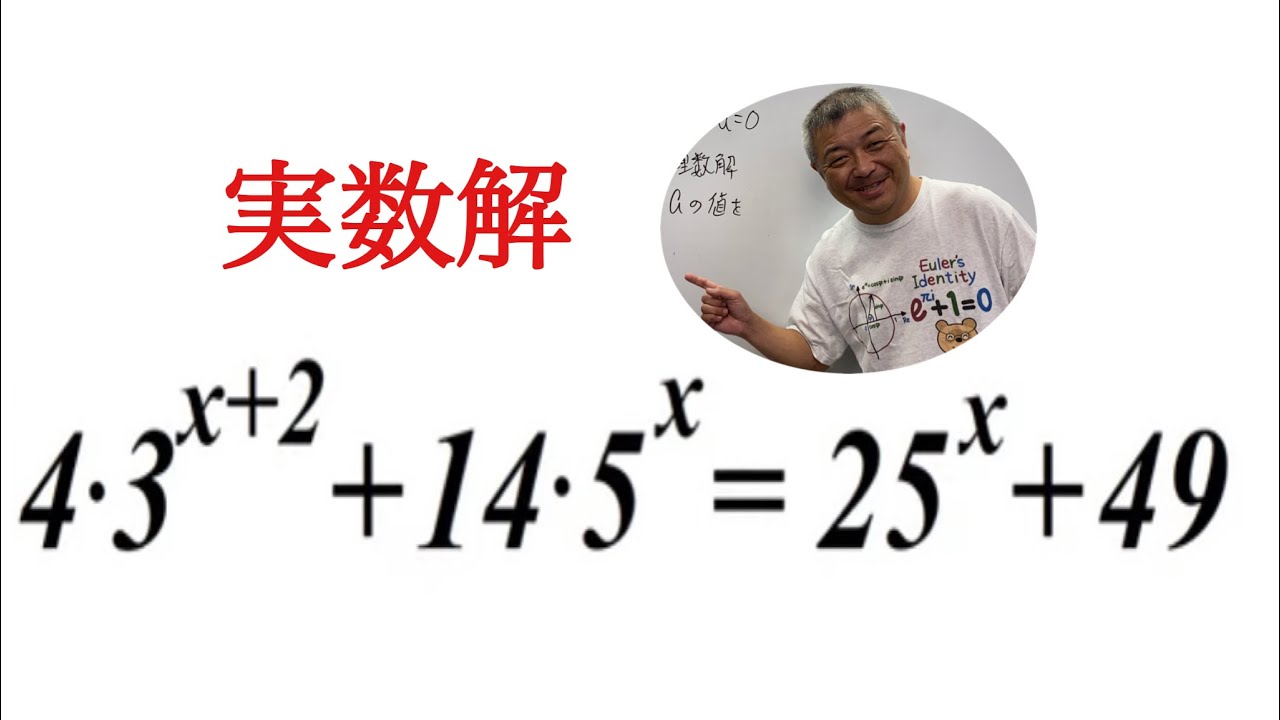
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$x$を求めよ.
$4・3^{x+2}+14・5^x~25^x+49$
この動画を見る
実数解$x$を求めよ.
$4・3^{x+2}+14・5^x~25^x+49$



