鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
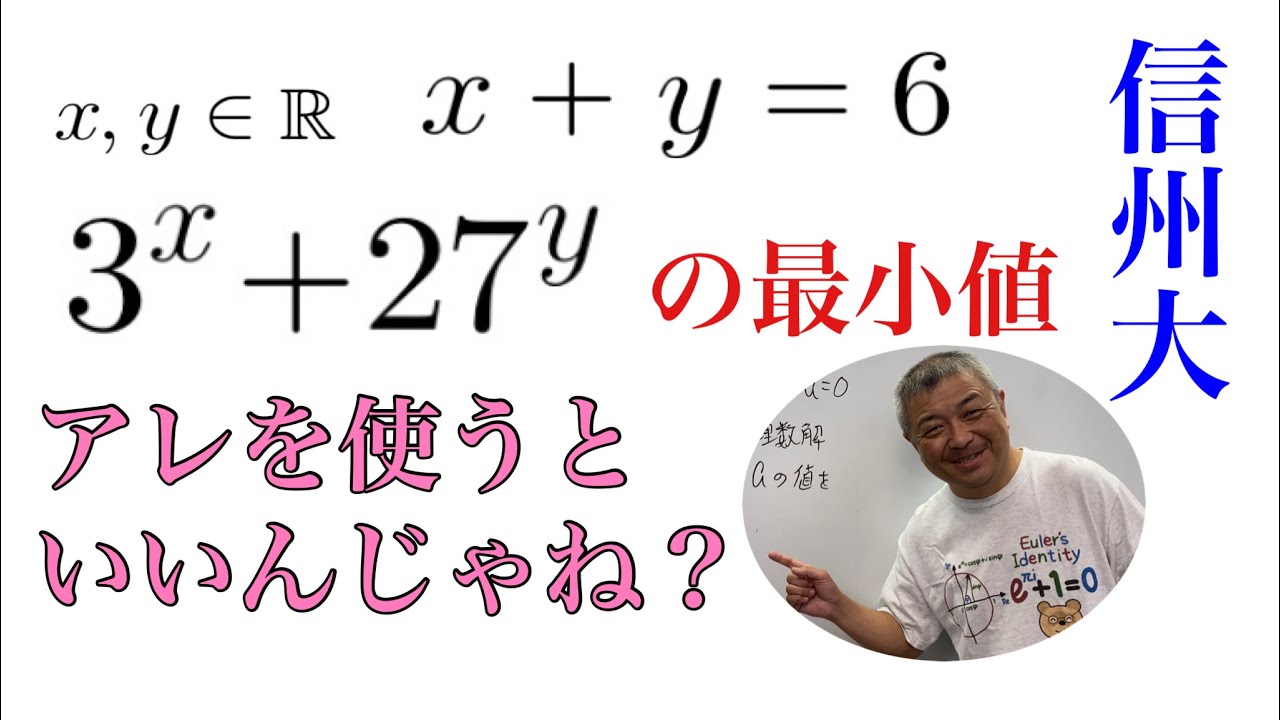
万能？倍数判定法！実用性は？
連立三元二次方程式 要ちょい工夫
単元：
#数と式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
解け
$
\begin{eqnarray}
\left\{
\begin{array}{l}
xy +x+ y = 49 \\
yz + y + z = 47\\
zx + z+x = 53
\end{array}
\right.
\end{eqnarray}
$
この動画を見る
解け
$
\begin{eqnarray}
\left\{
\begin{array}{l}
xy +x+ y = 49 \\
yz + y + z = 47\\
zx + z+x = 53
\end{array}
\right.
\end{eqnarray}
$
奈良女子大 基本定理の証明
単元：
#奈良女子大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022奈良女子大学過去問題
m,n整数
p,q,r実数(q$\neq$0)
$x^3+mx^2+nx+1=0$
はrとp+qiを解に持つ
(1)p-qiも解であることを示せ
(2)$r(p^2+q^2)=-1$を示せ
(3)|p+qi|= 1となる(m,n)をすべて求めよ
この動画を見る
2022奈良女子大学過去問題
m,n整数
p,q,r実数(q$\neq$0)
$x^3+mx^2+nx+1=0$
はrとp+qiを解に持つ
(1)p-qiも解であることを示せ
(2)$r(p^2+q^2)=-1$を示せ
(3)|p+qi|= 1となる(m,n)をすべて求めよ
超基本問題 対数方程式
ちょっと変わった漸化式 和歌山大
単元：
#数列#漸化式#和歌山大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022和歌山大学過去問題
$a_{1}=\frac{1}{2}$,$a_{n+1}=\frac{2}{1+a_{n}}$
$b_{1}=1$,$a_{n}b_{n+1}=b_{n}$
数列$b_{n}$の三項間漸化式をつくれ
$a_{n}$の一般項を求めよ
この動画を見る
2022和歌山大学過去問題
$a_{1}=\frac{1}{2}$,$a_{n+1}=\frac{2}{1+a_{n}}$
$b_{1}=1$,$a_{n}b_{n+1}=b_{n}$
数列$b_{n}$の三項間漸化式をつくれ
$a_{n}$の一般項を求めよ
高崎経済大 公式証明問題
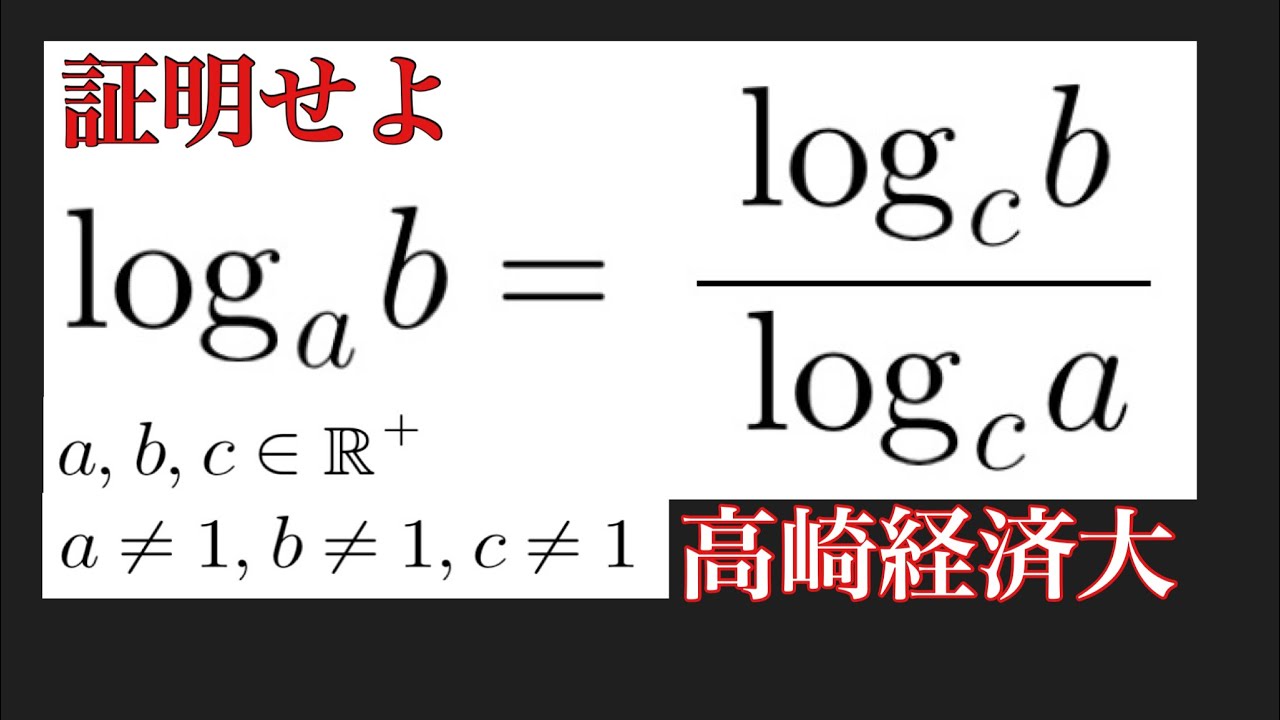
単元：
#学校別大学入試過去問解説(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023高崎経済大学過去問題
a,b,c正の実数
$a \neq1$,$b \neq 1$,$c \neq 1$
$\log_{a}b = \frac{\log_{c}b}{\log_{c}a}$
を証明せよ
この動画を見る
2023高崎経済大学過去問題
a,b,c正の実数
$a \neq1$,$b \neq 1$,$c \neq 1$
$\log_{a}b = \frac{\log_{c}b}{\log_{c}a}$
を証明せよ
愛媛大 解けないタイプの漸化式
単元：
#数列#愛媛大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023愛媛大学過去問題
$a_{1}=2$
$a_{n+1}=a_{n}^2+2(n=1,2,3,\cdots)$
mが自然数なら$a_{2m}$は6の倍数であることを示せ
この動画を見る
2023愛媛大学過去問題
$a_{1}=2$
$a_{n+1}=a_{n}^2+2(n=1,2,3,\cdots)$
mが自然数なら$a_{2m}$は6の倍数であることを示せ
順列 岡山県立大 続き
単元：
#大学入試過去問(数学)#場合の数と確率
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022岡山県立大学過去問題
●n個$(n \geqq 2)$と
○3個を1列に並べる
○●〇が現れる並べ方は何通りか
＊同じ色の玉は区別しない
この動画を見る
2022岡山県立大学過去問題
●n個$(n \geqq 2)$と
○3個を1列に並べる
○●〇が現れる並べ方は何通りか
＊同じ色の玉は区別しない
岡山県立大 順列
単元：
#場合の数と確率#学校別大学入試過去問解説(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022岡山県立大学過去問題
●n個$(n \geqq 2)$と
○3個を1列に並べる
○がとなり合う並べ方は何通りか
＊同じ色の玉は区別しない
この動画を見る
2022岡山県立大学過去問題
●n個$(n \geqq 2)$と
○3個を1列に並べる
○がとなり合う並べ方は何通りか
＊同じ色の玉は区別しない
複素数の基本問題 岡山県立大
単元：
#大学入試過去問(数学)#複素数と方程式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022岡山県立大学過去問題
$z=1+\sqrt{3}+(\sqrt{3}-1)i$
$z^{n}$が正の実数となる自然数nは100以下に何個あるか？
この動画を見る
2022岡山県立大学過去問題
$z=1+\sqrt{3}+(\sqrt{3}-1)i$
$z^{n}$が正の実数となる自然数nは100以下に何個あるか？
極限の基本問題 愛知県立大
単元：
#関数と極限#学校別大学入試過去問解説(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2019愛知県立大学過去問題
$e=\displaystyle \lim_{ h \to 0 } (1+h)^\frac{1}{h} $
aは正の実数
$e=\displaystyle \lim_{ x \to \infty } \frac{1}{x^{x}}(x-a)^{x}$
の値
この動画を見る
2019愛知県立大学過去問題
$e=\displaystyle \lim_{ h \to 0 } (1+h)^\frac{1}{h} $
aは正の実数
$e=\displaystyle \lim_{ x \to \infty } \frac{1}{x^{x}}(x-a)^{x}$
の値
虚数解を利用してcos144°を求める
単元：
#学校別大学入試過去問解説(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2020愛知県立大学過去問題
$x^5=1$
の虚数解を利用して$\cos144^\circ$の値を求めよ
この動画を見る
2020愛知県立大学過去問題
$x^5=1$
の虚数解を利用して$\cos144^\circ$の値を求めよ
どっちがでかい？(５^10+12^10)vs13^10
どっちがでかい？
４次方程式
単元：
#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
解け
$(6x-1)(3x-1)(2x-1)(x-1)+x^{2}-25 = 0$
この動画を見る
解け
$(6x-1)(3x-1)(2x-1)(x-1)+x^{2}-25 = 0$
兵庫県立大 不等式の証明
単元：
#兵庫県立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022兵庫県立大学過去問題
$a \geqq 0$,$b \geqq 0$,$c \geqq 0$のとき
$\frac{a+b+c}{3} \geqq \sqrt\frac{ab+bc+ca}{3}$
この動画を見る
2022兵庫県立大学過去問題
$a \geqq 0$,$b \geqq 0$,$c \geqq 0$のとき
$\frac{a+b+c}{3} \geqq \sqrt\frac{ab+bc+ca}{3}$
兵庫県立大 複素数の掛け算
単元：
#兵庫県立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022兵庫県立大学過去問題
a,b,c,dは整数
$a \geqq 0$,$a \geqq c$,$b \geqq d$
$(a+b\sqrt{5}i)(c+d\sqrt{5}i)=6$
①$(a^{2}+5b^{2})(c^{2}+5d^{2})=36$を示せ
②(a,b,c,d)の組をすべて求めよ
この動画を見る
2022兵庫県立大学過去問題
a,b,c,dは整数
$a \geqq 0$,$a \geqq c$,$b \geqq d$
$(a+b\sqrt{5}i)(c+d\sqrt{5}i)=6$
①$(a^{2}+5b^{2})(c^{2}+5d^{2})=36$を示せ
②(a,b,c,d)の組をすべて求めよ
ただの分数の和
単元：
#数列とその和（等差・等比・階差・Σ）
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\frac{1}{3}$+$\frac{1}{6}$+$\frac{1}{10}$+$\frac{1}{15}$+$\frac{1}{21}$+$\frac{1}{28}$+$\cdots$+$\frac{□}{□}$=?
＊分母の数は階差数列
この動画を見る
$\frac{1}{3}$+$\frac{1}{6}$+$\frac{1}{10}$+$\frac{1}{15}$+$\frac{1}{21}$+$\frac{1}{28}$+$\cdots$+$\frac{□}{□}$=?
＊分母の数は階差数列
Σ立法の和の公式を視覚的に
単元：
#数列とその和（等差・等比・階差・Σ）
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$1^3+2^3+\cdots+n^3=\{ \frac{n(n+1)}{2} \}^2$
$1^2+2^2+3^2+\cdots + n^2 = \frac{n(n+1)(2n+1)}{6}$
この動画を見る
$1^3+2^3+\cdots+n^3=\{ \frac{n(n+1)}{2} \}^2$
$1^2+2^2+3^2+\cdots + n^2 = \frac{n(n+1)(2n+1)}{6}$
日本獣医生命科学大 例のあれ
単元：
#数列
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022日本獣医生命科学大学過去問題
n自然数
$S_n = \frac{3}{a_1}+\frac{5}{a_2}+\frac{7}{a_3}+\cdots+\frac{2n+1}{a_n}$
$a_n = 1^2+2^2+3^2+\cdots+n^2$
$S_n$を求めよ
この動画を見る
2022日本獣医生命科学大学過去問題
n自然数
$S_n = \frac{3}{a_1}+\frac{5}{a_2}+\frac{7}{a_3}+\cdots+\frac{2n+1}{a_n}$
$a_n = 1^2+2^2+3^2+\cdots+n^2$
$S_n$を求めよ
東邦大（理）基本問題
単元：
#整数の性質
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023東邦大学過去問題
p,q整数
α+β =2P
αβ = 4q
$α^n+β^n$は$2^n$で割り切れることを示せ(n=1,2,3,$\cdots$)
この動画を見る
2023東邦大学過去問題
p,q整数
α+β =2P
αβ = 4q
$α^n+β^n$は$2^n$で割り切れることを示せ(n=1,2,3,$\cdots$)
東邦大 対数とΣの基本問題
単元：
#対数関数#数列
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023東邦大学過去問題
$\displaystyle\sum_{n=1}^{2023}\log_{10}\frac{5n+1}{5n-4}$の整数部分
この動画を見る
2023東邦大学過去問題
$\displaystyle\sum_{n=1}^{2023}\log_{10}\frac{5n+1}{5n-4}$の整数部分
虚数係数二次方程式
単元：
#複素数と方程式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$z^2+\frac{1+(2-\sqrt{3})i}{2}z+\frac{\sqrt{3}+i}{2}=0$を解け
＊この方程式の2解を解にもつ実数係数の4次方程式を作れ
この動画を見る
$z^2+\frac{1+(2-\sqrt{3})i}{2}z+\frac{\sqrt{3}+i}{2}=0$を解け
＊この方程式の2解を解にもつ実数係数の4次方程式を作れ
林俊介 語りかける東大数学
単元：
#対数関数#関数と極限
指導講師：
鈴木貫太郎
問題文全文(内容文)：
(1)$n\in Z+$
$g(x):=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x \vert \leq 1) \\
0 (\vert x \vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$f(x):$連続であり,$p,q \in R$
$\vert x\vert \leq \dfrac{1}{n}$でつねに$p\leq f(x)\leq q$
$p\leq n\dfrac{\displaystyle \int_{-1}^{1} g(nx) f(x) dx\leq q}{I}$を示せ.
(2)$ｈ(x)=:\begin{eqnarray}
\left\{
\begin{array}{l}
-\dfrac{\pi}{2}\sin(\pi x) (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
次の極限を求めよ.
$\displaystyle \lim_{n\to\infty} n^2\displaystyle \int_{-1}^{1} h(nx)\log(1+e^{x+1})dx $
(1)$g(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$p\leq n \displaystyle \int_{-1}^{1} g(nx) f(x)dx \leq q$
2015東大過去問
この動画を見る
(1)$n\in Z+$
$g(x):=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x \vert \leq 1) \\
0 (\vert x \vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$f(x):$連続であり,$p,q \in R$
$\vert x\vert \leq \dfrac{1}{n}$でつねに$p\leq f(x)\leq q$
$p\leq n\dfrac{\displaystyle \int_{-1}^{1} g(nx) f(x) dx\leq q}{I}$を示せ.
(2)$ｈ(x)=:\begin{eqnarray}
\left\{
\begin{array}{l}
-\dfrac{\pi}{2}\sin(\pi x) (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
次の極限を求めよ.
$\displaystyle \lim_{n\to\infty} n^2\displaystyle \int_{-1}^{1} h(nx)\log(1+e^{x+1})dx $
(1)$g(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$p\leq n \displaystyle \int_{-1}^{1} g(nx) f(x)dx \leq q$
2015東大過去問
旭川医科大2023確率問題
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
コインを繰り返し投げて同じ面が3回続けて出たら終了するとき、
n,(n+1),(n+2) 回目に表が出て終了する確率を$P_n$とおくとき、
$\displaystyle \sum_{n=1}^\infty P_n$
を求めよ
旭川医大過去問
この動画を見る
コインを繰り返し投げて同じ面が3回続けて出たら終了するとき、
n,(n+1),(n+2) 回目に表が出て終了する確率を$P_n$とおくとき、
$\displaystyle \sum_{n=1}^\infty P_n$
を求めよ
旭川医大過去問
東邦大（理）
単元：
#学校別大学入試過去問解説(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023東邦大学過去問題
θを求めよ
$9^{\sin^2θ}+9^{\cos^2θ}=6$
$0 \leqq θ \leqq \frac{\pi}{2}$
この動画を見る
2023東邦大学過去問題
θを求めよ
$9^{\sin^2θ}+9^{\cos^2θ}=6$
$0 \leqq θ \leqq \frac{\pi}{2}$
例のやつ
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
コインを繰り返し投げて同じ面が3回続けて出たら終了
$n,n+1,n+2$回目に表が出て終了する場合の数$A_n$
$A_n$を求めよ.
この動画を見る
コインを繰り返し投げて同じ面が3回続けて出たら終了
$n,n+1,n+2$回目に表が出て終了する場合の数$A_n$
$A_n$を求めよ.
整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
Pが7以上の素数なら
$P^4-1$は240
の倍数であること
を示せ
この動画を見る
Pが7以上の素数なら
$P^4-1$は240
の倍数であること
を示せ
東京海洋大 三次方程式
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#東京海洋大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3-12x^2+41x-m=0$
が3つの整数解をもつような
$m$をすべて求めよ。
東京海洋大過去問
この動画を見る
$x^3-12x^2+41x-m=0$
が3つの整数解をもつような
$m$をすべて求めよ。
東京海洋大過去問
東京海洋大 確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京海洋大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
8チームで下図のような トーナメント方式で大会 を行う。
※図は動画内参照
AvsBと他6vs他6はどちらも勝つ確率$\frac{1}{2}$。
Avs他6,Bvs他6はA,Bの勝つ確率$\frac{2}{3}$。
Aの優勝する確率は?
①Aをブロック1、Bをブロック2 に配置した場合
②8チームを無作為 に配置した場合
東京海洋大過去問
この動画を見る
8チームで下図のような トーナメント方式で大会 を行う。
※図は動画内参照
AvsBと他6vs他6はどちらも勝つ確率$\frac{1}{2}$。
Avs他6,Bvs他6はA,Bの勝つ確率$\frac{2}{3}$。
Aの優勝する確率は?
①Aをブロック1、Bをブロック2 に配置した場合
②8チームを無作為 に配置した場合
東京海洋大過去問