 九州大学
九州大学
 九州大学
九州大学
整数問題の難問!誘導ありでも難しいです【九州大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
自然数$m,n$が、$n^4=1+210m^2$ ・・・①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
この動画を見る
自然数$m,n$が、$n^4=1+210m^2$ ・・・①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
無限降下法って知ってる?整数問題の難問です【数学 入試問題】【九州大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを証明せよ。
九州大過去問
この動画を見る
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを証明せよ。
九州大過去問
九州大のナイスな問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\sqrt5-1+\sqrt{10+2\sqrt5}i$
$\beta=-\sqrt5-1+\sqrt{10-2\sqrt5}i$
(1)$\alpha$を解にもつ実数係数の2次方程式を1つ例示せよ.
(2)$\alpha,\beta$を解にもつ実数係数の4次方程式を1つ例示せよ.
(3)$\beta^5$の値を求めよ.
九州大(類)過去問
この動画を見る
$\alpha=\sqrt5-1+\sqrt{10+2\sqrt5}i$
$\beta=-\sqrt5-1+\sqrt{10-2\sqrt5}i$
(1)$\alpha$を解にもつ実数係数の2次方程式を1つ例示せよ.
(2)$\alpha,\beta$を解にもつ実数係数の4次方程式を1つ例示せよ.
(3)$\beta^5$の値を求めよ.
九州大(類)過去問
サイコロの確率の問題!注意点があります【数学 入試問題】【九州大学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
4個のサイコロを同時に投げるとき,出る目すべての積を$X$とする。
(1)$X$が25の倍数になる確率を求めよ。
(2)$X$が4の倍数になる確率を求めよ。
(3)$X$が100の倍数になる確率を求めよ。
九州大過去問
この動画を見る
4個のサイコロを同時に投げるとき,出る目すべての積を$X$とする。
(1)$X$が25の倍数になる確率を求めよ。
(2)$X$が4の倍数になる確率を求めよ。
(3)$X$が100の倍数になる確率を求めよ。
九州大過去問
あの公式が力を発揮する良問!微分・積分のよく出る問題です【数学 入試問題】【九州大学】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
この動画を見る
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
福田の数学〜九州大学2022年文系第4問〜定義に従って定積分の性質を証明する

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
定積分について述べた次の文章を読んで、後の問いに答えよ。
$f(x)$を整式とする。$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$#\int_a^bf(x)dx=F(b)-F(a)\ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、f(x),g(x),h(x)は整式、k,lは定数である。
以下、$f(x)$が区間$0 \leqq x \leqq 1$上で増加関数になる場合を考える。
$n$を自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、$n$を限りなく大きくすると$S_n$は$\int_0^1f(x)dx$に限りなく近づく。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことと定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と関数の増減と導関数の関係を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学文系過去問
この動画を見る
定積分について述べた次の文章を読んで、後の問いに答えよ。
$f(x)$を整式とする。$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$#\int_a^bf(x)dx=F(b)-F(a)\ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、f(x),g(x),h(x)は整式、k,lは定数である。
以下、$f(x)$が区間$0 \leqq x \leqq 1$上で増加関数になる場合を考える。
$n$を自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、$n$を限りなく大きくすると$S_n$は$\int_0^1f(x)dx$に限りなく近づく。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことと定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と関数の増減と導関数の関係を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学文系過去問
福田の数学〜九州大学2022年文系第3問〜高次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$k$を実数とし、整式f(x)を
$f(x)=x^4+6x^3-kx^2+2kx-64$
で定める。方程式$f(x)=0$が虚数解をもつとき、以下の問いに答えよ。
(1)f(x)は$x-2$で割り切れることを示せ。
(2)方程式$f(x)=0$は負の実数解をもつことを示せ。
(3)方程式$f(x)=0$の全ての実数解が整数であり、
すべての虚数解の実部と虚部が共に整数であるとする。
このような$k$を全て求めよ。
2022九州大学文系過去問
この動画を見る
$k$を実数とし、整式f(x)を
$f(x)=x^4+6x^3-kx^2+2kx-64$
で定める。方程式$f(x)=0$が虚数解をもつとき、以下の問いに答えよ。
(1)f(x)は$x-2$で割り切れることを示せ。
(2)方程式$f(x)=0$は負の実数解をもつことを示せ。
(3)方程式$f(x)=0$の全ての実数解が整数であり、
すべての虚数解の実部と虚部が共に整数であるとする。
このような$k$を全て求めよ。
2022九州大学文系過去問
福田の数学〜九州大学2022年文系第2問〜点と平面の距離と対称点

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
座標空間内の4点
$O(0,0,0),A(1,1,0),B(2,1,2),P(4,0,-1)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }$,
$\overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a },\ \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、大きさが1
のベクトル$\overrightarrow{ n }$を求めよ。
(2)点Pから平面$\alpha$に垂線を下ろし、その交点をQとおく。
線分PQの長さを求めよ。
(3)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
2022九州大学文系過去問
この動画を見る
座標空間内の4点
$O(0,0,0),A(1,1,0),B(2,1,2),P(4,0,-1)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }$,
$\overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a },\ \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、大きさが1
のベクトル$\overrightarrow{ n }$を求めよ。
(2)点Pから平面$\alpha$に垂線を下ろし、その交点をQとおく。
線分PQの長さを求めよ。
(3)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
2022九州大学文系過去問
福田の数学〜九州大学2022年理系第5問の背景を考える〜内サイクロイド曲線(ハイポサイクロイド、アステロイド)の媒介変数表示

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上の曲線#ベクトルと平面図形、ベクトル方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#九州大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
xy平面上の曲線Cを、媒介変数tを用いて次のように定める。
$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
この動画を見る
xy平面上の曲線Cを、媒介変数tを用いて次のように定める。
$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
福田の数学〜九州大学2022年文系第1問〜絶対値の付いた放物線と直線で囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#2次関数#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
この動画を見る
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
福田の数学〜九州大学2022年理系第5問〜媒介変数表示のグラフの対称性とグラフの追跡

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#九州大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$xy$平面上の曲線Cを、媒介変数tを用いて次のように定める。$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
この動画を見る
$xy$平面上の曲線Cを、媒介変数tを用いて次のように定める。$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第4問〜定積分の定義から性質を証明する

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
定積分について述べた次の文章を読んで、後の問いに答えよ。
区間$a \leqq x \leqq b$で連続な関数f(x)に対して$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$\int_a^bf(x)dx=F(b)-F(a) \ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$ a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、$f(x),g(x),h(x)$は区間$a \leqq x \leqq b$で連続な関数、$k,l$は定数である。
以下、$f(x)$を区間$0 \leqq x \leqq 1$で連続な増加関数とし、
nを自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、はさみうちの原理より$\lim_{n \to \infty}S_n=\int_0^1f(x)dx$が成り立つ。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことを、導関数の定義に従って示せ。
また、この等式と定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と平均値の定理を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学理系過去問
この動画を見る
定積分について述べた次の文章を読んで、後の問いに答えよ。
区間$a \leqq x \leqq b$で連続な関数f(x)に対して$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$\int_a^bf(x)dx=F(b)-F(a) \ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$ a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、$f(x),g(x),h(x)$は区間$a \leqq x \leqq b$で連続な関数、$k,l$は定数である。
以下、$f(x)$を区間$0 \leqq x \leqq 1$で連続な増加関数とし、
nを自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、はさみうちの原理より$\lim_{n \to \infty}S_n=\int_0^1f(x)dx$が成り立つ。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことを、導関数の定義に従って示せ。
また、この等式と定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と平均値の定理を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第3問〜約数と倍数と不定方程式の自然数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
自然数m,nが
$n^4=1+210m^2 \ldots①$
を満たすとき、以下の問いに答えよ。
(1)$\frac{n^2+1}{2},\ \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
(2)$n^2-1$は168の倍数であることを示せ。
(3)①を満たす自然数の組(m,n)を1つ求めよ。
2022九州大学理系過去問
この動画を見る
自然数m,nが
$n^4=1+210m^2 \ldots①$
を満たすとき、以下の問いに答えよ。
(1)$\frac{n^2+1}{2},\ \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
(2)$n^2-1$は168の倍数であることを示せ。
(3)①を満たす自然数の組(m,n)を1つ求めよ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第2問〜商と余りの関係と極限

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
この動画を見る
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第1問〜空間における折れ線の最小〜平面の方程式を勉強するよ!

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
座標空間内の5点
$O(0,0,0), A(1,1,0), B(2,1,2), P(4,0,-1), Q(4,0,5)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }, \overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a }, \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、
大きさが1のベクトル$\overrightarrow{ n }$を求めよ。
(2)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
(3)点Rが平面$\alpha$上を動くとき、$|\overrightarrow{ PR }|+|\overrightarrow{ RQ }|$が最小となるような
点Rの座標を求めよ。
2022九州大学理系過去問
この動画を見る
座標空間内の5点
$O(0,0,0), A(1,1,0), B(2,1,2), P(4,0,-1), Q(4,0,5)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }, \overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a }, \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、
大きさが1のベクトル$\overrightarrow{ n }$を求めよ。
(2)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
(3)点Rが平面$\alpha$上を動くとき、$|\overrightarrow{ PR }|+|\overrightarrow{ RQ }|$が最小となるような
点Rの座標を求めよ。
2022九州大学理系過去問
【誘導形式:概要欄】大学入試問題#181 九州大学改(1987) 定積分 ウォリス積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^8\sqrt{ 1-x^2 }\ dx$
出典:1987年九州大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^8\sqrt{ 1-x^2 }\ dx$
出典:1987年九州大学 入試問題
2022九州大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
kは実数であり,整式f(x)を$ f(x)=x^4+6x^3-kx^2+2kx-64 $で定める.
f(x)=0が虚数解をもつとき,
(1)f(x)はx-2で割り切れることを示せ.
(2)f(x)=0は負の実数解をもつことを示せ.
(3)f(x)=0のすべての実数解が整数で,すべての虚数解の実部と虚部が
ともに整数である.kの値を求めよ.
2022九州大過去問
この動画を見る
kは実数であり,整式f(x)を$ f(x)=x^4+6x^3-kx^2+2kx-64 $で定める.
f(x)=0が虚数解をもつとき,
(1)f(x)はx-2で割り切れることを示せ.
(2)f(x)=0は負の実数解をもつことを示せ.
(3)f(x)=0のすべての実数解が整数で,すべての虚数解の実部と虚部が
ともに整数である.kの値を求めよ.
2022九州大過去問
2022九州大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数m,nは$ n^4=1+210m^2 $を満たす.
(1)$\dfrac{n^2+1}{2},\dfrac{n^2-1}{2}$は互いに素な整数であることを示せ.
(2)$ n^2-1 $は168の倍数であることを示せ.
(3)(m,n)を1組求めよ.
2022九州大過去問
この動画を見る
自然数m,nは$ n^4=1+210m^2 $を満たす.
(1)$\dfrac{n^2+1}{2},\dfrac{n^2-1}{2}$は互いに素な整数であることを示せ.
(2)$ n^2-1 $は168の倍数であることを示せ.
(3)(m,n)を1組求めよ.
2022九州大過去問
数学「大学入試良問集」【16−6 複素数平面と軌跡・回転移動】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$0 \lt a \lt 1$である定数$a$に対し、複素数平面上で$z=t+ai(t$は実数全体を動く$)$が表す直線を$l$とする。
ただし、$i$は虚数単位である。
(1)
複素数$z$が$l$上を動くとき、$z^2$が表す点の軌跡を図示せよ。
(2)
直線$l$を、原点を中心に角$\theta$だけ回転移動した直線を$m$とする。
$m$と(1)で求めた軌跡との交点の個数を$\sin\theta$の値で場合分けして求めよ。
この動画を見る
$0 \lt a \lt 1$である定数$a$に対し、複素数平面上で$z=t+ai(t$は実数全体を動く$)$が表す直線を$l$とする。
ただし、$i$は虚数単位である。
(1)
複素数$z$が$l$上を動くとき、$z^2$が表す点の軌跡を図示せよ。
(2)
直線$l$を、原点を中心に角$\theta$だけ回転移動した直線を$m$とする。
$m$と(1)で求めた軌跡との交点の個数を$\sin\theta$の値で場合分けして求めよ。
数学「大学入試良問集」【17−6 直線上の点の極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$f(x)=-\displaystyle \frac{1}{2}x+3$とする。
$x_1=1$とおいて数列$x_n=f(x_{n-1})$ $n=2,3,・・・$をつくり、平面座標上に点$P_n(x_n,f(x_n))$をとる。
このとき、次の各問いに答えよ。
(1)
数列$\{x_n\}$の一般項$x_n$を求めよ。
(2)
動点$P$が点$P_1$を出発して、$P_2,P_3,・・・,P_n,・・・$と進むとき、動点$P$はどのような点に近づくか。
その座標を求めよ。
(3)
線分$P_nP_{n+1}$の長さを$l_n$ $n=1,2,3,・・・$とする。
$L=\displaystyle \sum_{n=1}^n l_n$を求めよ。
この動画を見る
$f(x)=-\displaystyle \frac{1}{2}x+3$とする。
$x_1=1$とおいて数列$x_n=f(x_{n-1})$ $n=2,3,・・・$をつくり、平面座標上に点$P_n(x_n,f(x_n))$をとる。
このとき、次の各問いに答えよ。
(1)
数列$\{x_n\}$の一般項$x_n$を求めよ。
(2)
動点$P$が点$P_1$を出発して、$P_2,P_3,・・・,P_n,・・・$と進むとき、動点$P$はどのような点に近づくか。
その座標を求めよ。
(3)
線分$P_nP_{n+1}$の長さを$l_n$ $n=1,2,3,・・・$とする。
$L=\displaystyle \sum_{n=1}^n l_n$を求めよ。
高専数学 微積I #218 曲線の長さの最小値 (九州大学類題)
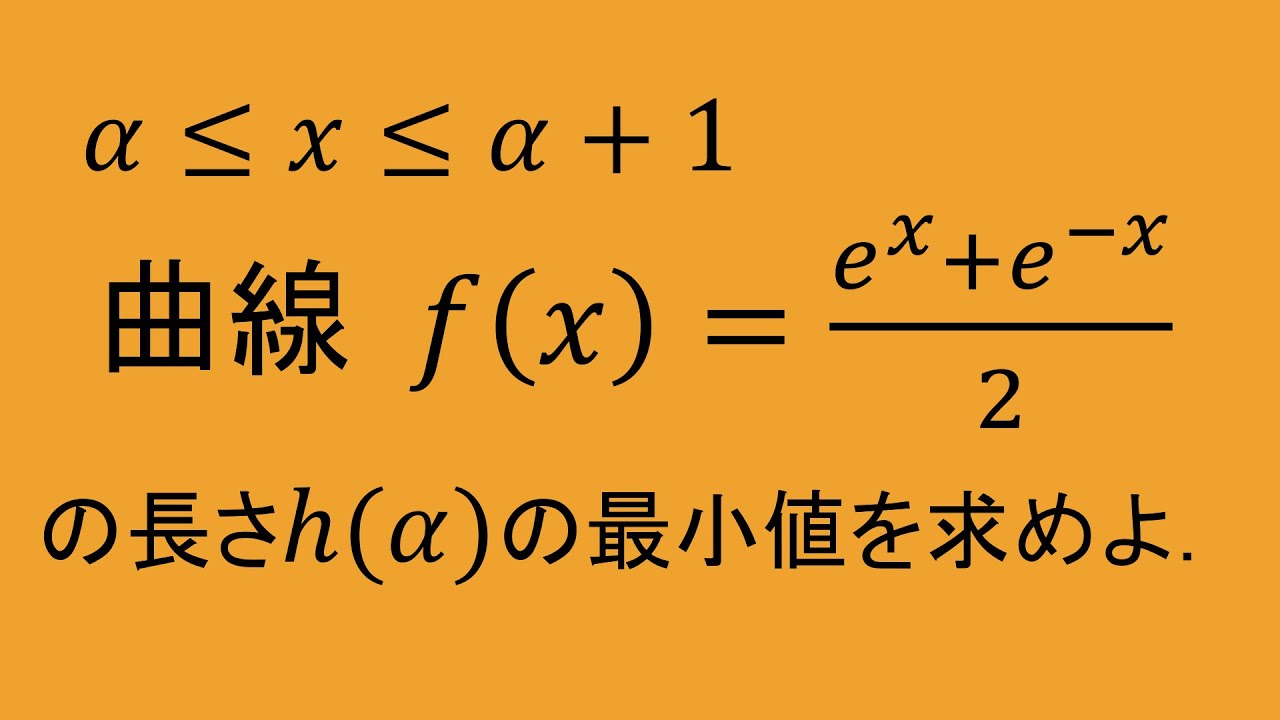
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\dfrac{e^x+e^{-x}}{2} \ (\alpha \leqq x \leqq \alpha+1)$
の曲線の長さ$k(\alpha)$の最小値を求めよ.
この動画を見る
$f(x)=\dfrac{e^x+e^{-x}}{2} \ (\alpha \leqq x \leqq \alpha+1)$
の曲線の長さ$k(\alpha)$の最小値を求めよ.
九州大 三次方程式と無理数

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\cos2 0^{ \circ }+i \sin20^{ \circ }$
$\alpha=z+\bar{ z }$
(1)
$\alpha$を解に持つ整数、係数の3次方程式を求めよ
(2)
(1)で求めた方程式は相異なる3つの実数解をもち、それらはすべて無理数となることを示せ
(3)
$\alpha$を解にもつ有理数係数の2次方程式はないことを示せ
出典:2000年九州大学 過去問
この動画を見る
$z=\cos2 0^{ \circ }+i \sin20^{ \circ }$
$\alpha=z+\bar{ z }$
(1)
$\alpha$を解に持つ整数、係数の3次方程式を求めよ
(2)
(1)で求めた方程式は相異なる3つの実数解をもち、それらはすべて無理数となることを示せ
(3)
$\alpha$を解にもつ有理数係数の2次方程式はないことを示せ
出典:2000年九州大学 過去問
九州大 COS7.5° 複素数
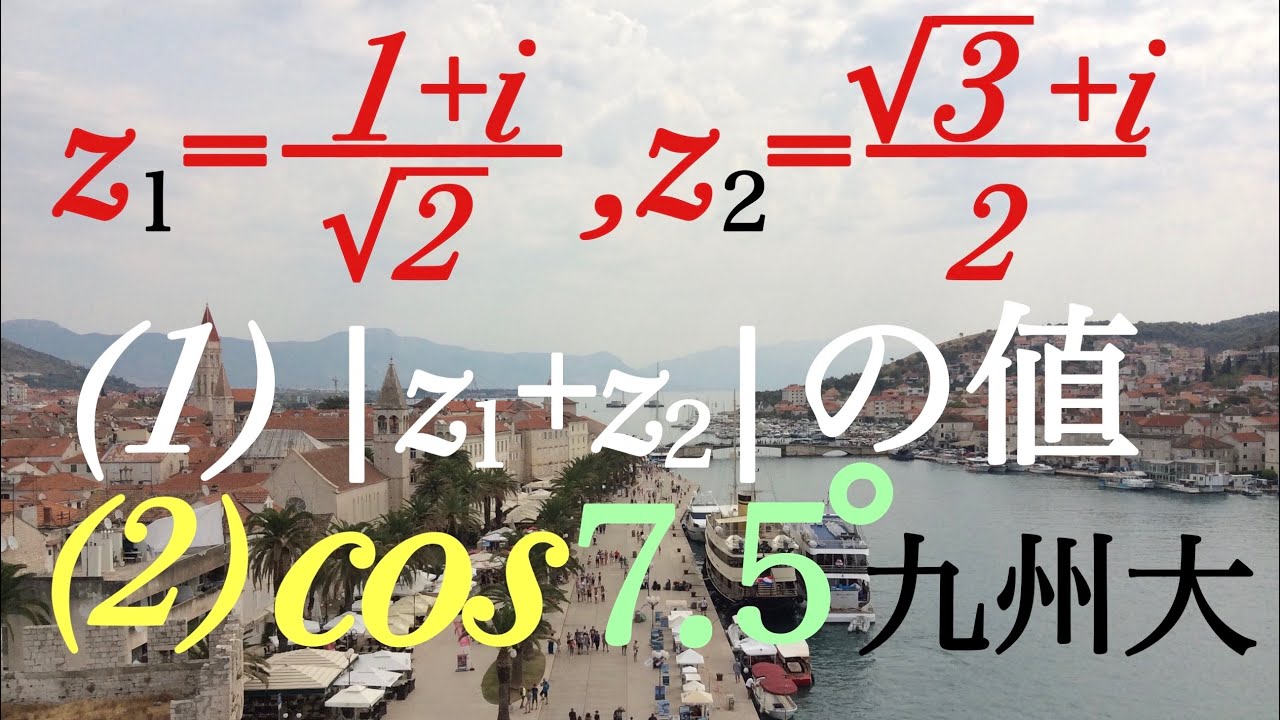
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z_1=\displaystyle \frac{1+i}{\sqrt{ 2 }},z_2=\displaystyle \frac{\sqrt{ 3 }+i}{2}$
(1)
$|z_1+z_2|$の値を求めよ
(2)
$\cos 7.5^{ \circ }$を求めよ
出典:1972年九州大学 過去問
この動画を見る
$z_1=\displaystyle \frac{1+i}{\sqrt{ 2 }},z_2=\displaystyle \frac{\sqrt{ 3 }+i}{2}$
(1)
$|z_1+z_2|$の値を求めよ
(2)
$\cos 7.5^{ \circ }$を求めよ
出典:1972年九州大学 過去問
九州大 虚数解を持つ4次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\sqrt{ 5 }-1+\sqrt{ 10+2\sqrt{ 5 } }i$
$\beta=-\sqrt{ 5 }-1+\sqrt{ 10-2\sqrt{ 5 } }i$
(1)
$\alpha,\beta$の両方を解にもつ実数係数の4次方程式を求めよ
(2)
$\beta^5$の値を求めよ
出典:1999年九州大学 過去問
この動画を見る
$\alpha=\sqrt{ 5 }-1+\sqrt{ 10+2\sqrt{ 5 } }i$
$\beta=-\sqrt{ 5 }-1+\sqrt{ 10-2\sqrt{ 5 } }i$
(1)
$\alpha,\beta$の両方を解にもつ実数係数の4次方程式を求めよ
(2)
$\beta^5$の値を求めよ
出典:1999年九州大学 過去問
九州大 三次関数 積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3+ax^2+bx+c(c \gt 0)$は$(c,0)$で$x$軸と接する。
$f(x)$と$x$軸とで囲まれる面積が最小となる$c$の値を求めよ
出典:2018年九州大学 過去問
この動画を見る
$f(x)=x^3+ax^2+bx+c(c \gt 0)$は$(c,0)$で$x$軸と接する。
$f(x)$と$x$軸とで囲まれる面積が最小となる$c$の値を求めよ
出典:2018年九州大学 過去問
九州大 三次関数 極値の差 ヨビノリ技

単元:
#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3-kx^2+kx+1$が極大値・極小値をもち、その差が$4|k|^3$
$k$の値を求めよ
出典:2019年九州大学 過去問
この動画を見る
$f(x)=x^3-kx^2+kx+1$が極大値・極小値をもち、その差が$4|k|^3$
$k$の値を求めよ
出典:2019年九州大学 過去問
九州大 整数問題 良問再投稿

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
文系
$2^{p-1}-1=p^k$
$p$素数、$k$非負整数
理系
$2^{p-1}-1=pq^2$
$p,q$素数
出典:2015年九州大学 過去問
この動画を見る
文系
$2^{p-1}-1=p^k$
$p$素数、$k$非負整数
理系
$2^{p-1}-1=pq^2$
$p,q$素数
出典:2015年九州大学 過去問
九州大 係数三乗根の三次方程式の解の個数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a \in \mathbb{R}(a$は実数$)$
$x^3-3\sqrt[ 3 ]{ 4-a^2 }x+2=0$
実数解の個数
出典:1964年九州大学 過去問
この動画を見る
$a \in \mathbb{R}(a$は実数$)$
$x^3-3\sqrt[ 3 ]{ 4-a^2 }x+2=0$
実数解の個数
出典:1964年九州大学 過去問
ヨビノリのマンデー積分をぶっ飛ばせ!刺客は本人

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$自然数、$x,y$実数
$\displaystyle \int_{0}^{ 1 } (\sin(2n\pi t)-xt-y)^2dt$の最小値を$I_n$とおく
$\displaystyle \lim_{ n \to \infty }I_n$を求めよ
出典:2019年九州大学 過去問
この動画を見る
$n$自然数、$x,y$実数
$\displaystyle \int_{0}^{ 1 } (\sin(2n\pi t)-xt-y)^2dt$の最小値を$I_n$とおく
$\displaystyle \lim_{ n \to \infty }I_n$を求めよ
出典:2019年九州大学 過去問
九州大 良問再投稿 合成公式

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sin 10^{ \circ }$は$8x^3-6x+1=0$の解であることを示し、他の2解も求めよ
出典:1975年九州大学 過去問
この動画を見る
$\sin 10^{ \circ }$は$8x^3-6x+1=0$の解であることを示し、他の2解も求めよ
出典:1975年九州大学 過去問
