学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜慶應義塾大学看護医療学部2025第2問(1)〜極形式とド・モアブルの定理
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
(1)$x^3-3x^2+6x-4=0$の解で
虚部が正であるものを$\omega$としたとき、
$\omega$の絶対値は$\vert \omega \vert=\boxed{キ}$であり、
偏角$\theta$は$\theta=\boxed{ク}$である。
ただし、$0\leqq \theta \lt 2\pi$とする。
また、$\omega^{10} =\boxed{ケ}+\boxed{コ}i$である。
ただし、$\boxed{ケ},\boxed{コ}$は実数とする。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{2}$
(1)$x^3-3x^2+6x-4=0$の解で
虚部が正であるものを$\omega$としたとき、
$\omega$の絶対値は$\vert \omega \vert=\boxed{キ}$であり、
偏角$\theta$は$\theta=\boxed{ク}$である。
ただし、$0\leqq \theta \lt 2\pi$とする。
また、$\omega^{10} =\boxed{ケ}+\boxed{コ}i$である。
ただし、$\boxed{ケ},\boxed{コ}$は実数とする。
$2025$年慶應義塾大学看護医療学部過去問題
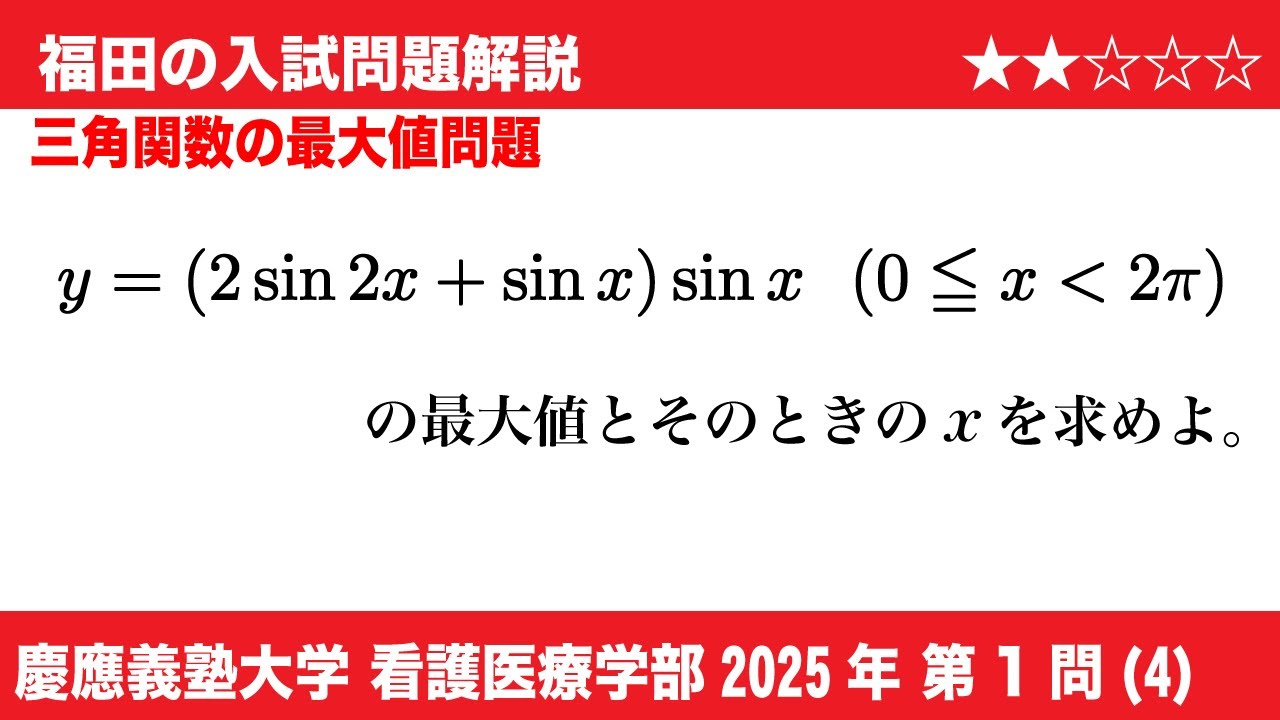
福田の数学〜慶應義塾大学看護医療学部2025第1問(4)〜三角関数の最大
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)関数$y=(2\sin 2x+\sin x)+\sin x (0\leqq x \lt 2\pi)$は、
$x=\boxed{オ}$のとき最大値$\boxed{カ}$をとる。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(4)関数$y=(2\sin 2x+\sin x)+\sin x (0\leqq x \lt 2\pi)$は、
$x=\boxed{オ}$のとき最大値$\boxed{カ}$をとる。
$2025$年慶應義塾大学看護医療学部過去問題
福田の数学〜慶應義塾大学看護医療学部2025第1問(3)〜反復試行の確率と条件付き確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)さいころを$6$回続けて投げる。
$3$の倍数の目が出る回数が$2$になる確率は
$\boxed{ウ}$である。
また、$3$の倍数の目が出た回数が$2$であったとき、
その$2$回が続けて起こる条件付き確率は$\boxed{エ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(3)さいころを$6$回続けて投げる。
$3$の倍数の目が出る回数が$2$になる確率は
$\boxed{ウ}$である。
また、$3$の倍数の目が出た回数が$2$であったとき、
その$2$回が続けて起こる条件付き確率は$\boxed{エ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
1都3県のFラン大学一覧 #shorts
単元：
#大学入試過去問(数学)#物理#化学#生物#学校別大学入試過去問解説(数学)#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#大学入試過去問(英語)#大学入試過去問(国語)#学校別大学入試過去問解説(英語)#大学入試過去問(生物)#数学(高校生)#理科(高校生)
指導講師：
Morite2 English Channel
問題文全文(内容文)：
速報！2025年最新版、1都3県のヤバすぎるFラン大学リストが公開され、受験界騒然！まさかのあの大学の名前が並んでいるぞ。
このリストには、人気クリエイターの藤川天が過去に**不合格になった大学**が続々登場している。具体的には、火越大学、神奈川歯科大学、そして埼玉工業大学が、藤川天が受験して落ちた場所として挙げられている。
リストには他にも、上野学園大学や東京女学館大学といった「もうなくなった」大学の名前も含まれている。また、東京音楽大学のような大学は、判定できない「別枠」としてリストに登場しているが、これには賛否の声もあるようだ。
特にネットで話題を呼んでいるのが、フェリス女学院大学のランクイン。慶応とインカレしているイメージがあるのに、こんなに下なの!?と驚きの声が上がっている。さらに、アニメや映画で架空の大学名として使われる「東都大学」が実在していたという衝撃の事実も判明したぞ。
この動画を見る
速報！2025年最新版、1都3県のヤバすぎるFラン大学リストが公開され、受験界騒然！まさかのあの大学の名前が並んでいるぞ。
このリストには、人気クリエイターの藤川天が過去に**不合格になった大学**が続々登場している。具体的には、火越大学、神奈川歯科大学、そして埼玉工業大学が、藤川天が受験して落ちた場所として挙げられている。
リストには他にも、上野学園大学や東京女学館大学といった「もうなくなった」大学の名前も含まれている。また、東京音楽大学のような大学は、判定できない「別枠」としてリストに登場しているが、これには賛否の声もあるようだ。
特にネットで話題を呼んでいるのが、フェリス女学院大学のランクイン。慶応とインカレしているイメージがあるのに、こんなに下なの!?と驚きの声が上がっている。さらに、アニメや映画で架空の大学名として使われる「東都大学」が実在していたという衝撃の事実も判明したぞ。
福田の数学〜慶應義塾大学看護医療学部2025第1問(2)〜対数不等式
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)不等式$2(\log_3 x)^2+2\log_9 x \gt 1$を解くと
$\boxed{イ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(2)不等式$2(\log_3 x)^2+2\log_9 x \gt 1$を解くと
$\boxed{イ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
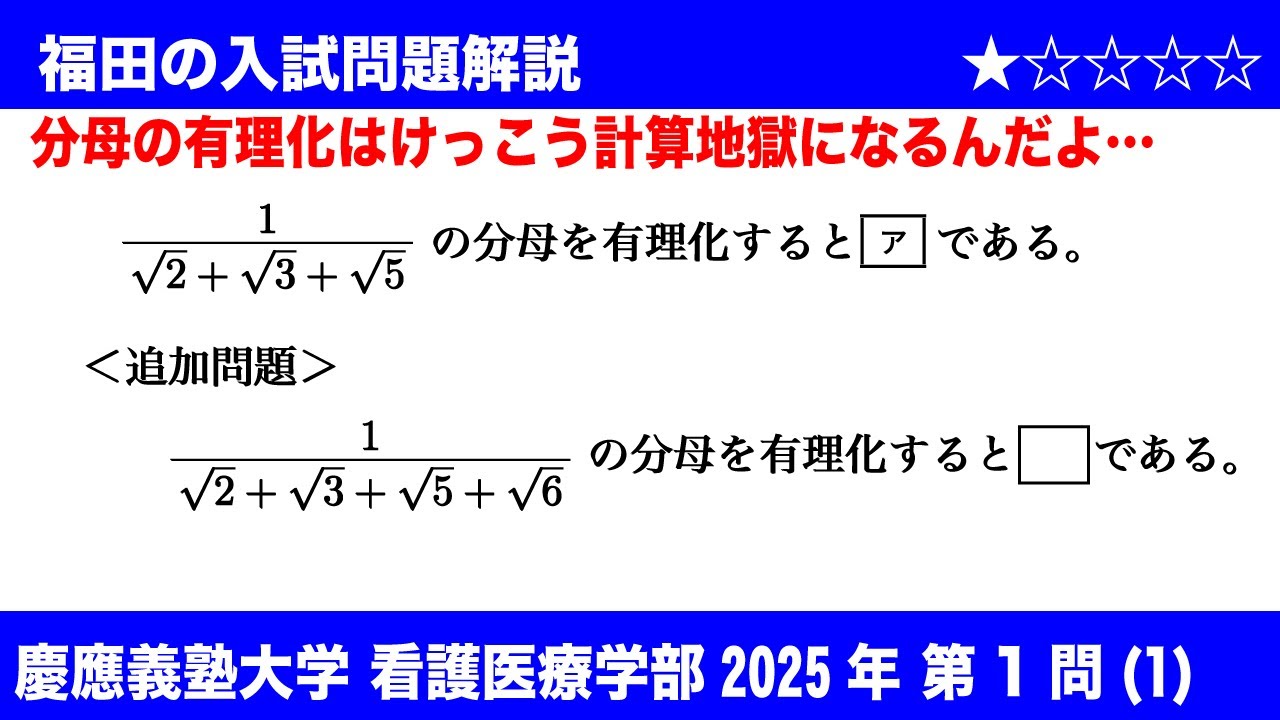
福田の数学〜慶應義塾大学看護医療学部2025第1問(1)〜分母の有理化
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5}$の分母を有理化すると
$\boxed{ア}$である。
〈追加問題〉
$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5+\sqrt6}$の分母を有理化すると
$\Box$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(1)$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5}$の分母を有理化すると
$\boxed{ア}$である。
〈追加問題〉
$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5+\sqrt6}$の分母を有理化すると
$\Box$である。
$2025$年慶應義塾大学看護医療学部過去問題
福田の数学〜早稲田大学理工学部2025第5問〜無理関数のグラフ上に無数の有理点が存在する証明
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$xy$平面上の曲線$C:y=\sqrt[3]{x^2+2}$と考え、
$C$上の$(0,\sqrt[3]{2})$以外の点$P(a,b)$における接線を
$\ell : y = kx +c$と表す。$C$と$\ell$の方程式から
$x$を消去して得られる$y$についての$3$次方程式
$f(y)=0$は$b$を重解としてもつので、もう$1$つの解を
$b'$とする。
ただし、$b'$が$3$重解のときは$b'=b$とみなす。
次の問いに答えよ。
(1)$2b+b'$を$k$のみの分数式で表せ。
(2)$b'$を$b$のみの分数式で表せ。
(3)$C$と$\ell$の共有点で、その$y$座標が$b'$であるものを
$P'(a',b')$とする。
$a$と$b$が有理数ならば、$a'$と$b'$も有理数であることを
示せ。
(4)$b$が奇数$p,q$と負でない整数$r$を用いて
$b=\dfrac{p}{2^r q}$で与えられるとする。
有理数$b'$を奇数$p',q'$と整数$s$を用いて$b'=\dfrac{p'}{2^s q'}$と
表すとき、$s$を$r$の式で表せ。
(5)$P(5,3)$が曲線$C$上の点であることを利用して、
$C$上に$x$座標と$y$座標がともに有理数であるような点が
無数に存在することを示せ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{5}$
$xy$平面上の曲線$C:y=\sqrt[3]{x^2+2}$と考え、
$C$上の$(0,\sqrt[3]{2})$以外の点$P(a,b)$における接線を
$\ell : y = kx +c$と表す。$C$と$\ell$の方程式から
$x$を消去して得られる$y$についての$3$次方程式
$f(y)=0$は$b$を重解としてもつので、もう$1$つの解を
$b'$とする。
ただし、$b'$が$3$重解のときは$b'=b$とみなす。
次の問いに答えよ。
(1)$2b+b'$を$k$のみの分数式で表せ。
(2)$b'$を$b$のみの分数式で表せ。
(3)$C$と$\ell$の共有点で、その$y$座標が$b'$であるものを
$P'(a',b')$とする。
$a$と$b$が有理数ならば、$a'$と$b'$も有理数であることを
示せ。
(4)$b$が奇数$p,q$と負でない整数$r$を用いて
$b=\dfrac{p}{2^r q}$で与えられるとする。
有理数$b'$を奇数$p',q'$と整数$s$を用いて$b'=\dfrac{p'}{2^s q'}$と
表すとき、$s$を$r$の式で表せ。
(5)$P(5,3)$が曲線$C$上の点であることを利用して、
$C$上に$x$座標と$y$座標がともに有理数であるような点が
無数に存在することを示せ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜早稲田大学理工学部2025第4問〜4つの互いに外接する球面の中心が作る四面体の体積
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#体積・表面積・回転体・水量・変化のグラフ#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
空間内に原点$O$を中心とする半径$r$の球面$S$がある。
さらに、半径が$1,2,3$の球面$S_1,S_2,S_3$があり、
これら$4$つの球面のうち
どの$2$つの球面も互いに外接している。
$S_1,S_2,S_3$中心を順に$P_1,P_2,P_3$とし、
$O,P_1,P_2,P_3$は同一平面上にないとする。
さらに、球面$S$が球面$S_1,S_2,S_3$と
接する$3$つの点と、
$\overrightarrow{OQ}=\dfrac{1}{4}(\overrightarrow{OP_1}+\overrightarrow{OP_2}+\overrightarrow{OP_3})$
により定まる点$Q$は、同一平面上にあるとする。
次の問いに答えよ。
(1)$r$の値を求めよ。
(2)四面体$OP_1P_2P_3$の体積を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{4}$
空間内に原点$O$を中心とする半径$r$の球面$S$がある。
さらに、半径が$1,2,3$の球面$S_1,S_2,S_3$があり、
これら$4$つの球面のうち
どの$2$つの球面も互いに外接している。
$S_1,S_2,S_3$中心を順に$P_1,P_2,P_3$とし、
$O,P_1,P_2,P_3$は同一平面上にないとする。
さらに、球面$S$が球面$S_1,S_2,S_3$と
接する$3$つの点と、
$\overrightarrow{OQ}=\dfrac{1}{4}(\overrightarrow{OP_1}+\overrightarrow{OP_2}+\overrightarrow{OP_3})$
により定まる点$Q$は、同一平面上にあるとする。
次の問いに答えよ。
(1)$r$の値を求めよ。
(2)四面体$OP_1P_2P_3$の体積を求めよ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜早稲田大学理工学部2025第3問〜完全順列と漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$1$から$n$までの異なる自然数が$1$つずつ書かれた
$n$枚のカードが一列に並んでいる。
このとき、
どのカードも現在とは異なる位置に移動するよう
並べ替えてできる順列の総数を$a_n$で表し、
並べ方の総数$n!$に閉める$a_n$の割合を$p_n$で表す。
例えば、$a_1=0,p_1=0,a_2=1,p_2=\dfrac{1}{2},$
$a_3=2,p_3=\dfrac{1}{3}$である。
(1)$a_4$の値を求めよ。
(2)$n\geqq 3$のとき、$a_n$を$a_{n-1}$と
$a_{n-2}$を用いて表せ。
(3)$n\geqq 2$のとき、$p_n-p_{n-1}$を
$n$を用いて表せ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{3}$
$1$から$n$までの異なる自然数が$1$つずつ書かれた
$n$枚のカードが一列に並んでいる。
このとき、
どのカードも現在とは異なる位置に移動するよう
並べ替えてできる順列の総数を$a_n$で表し、
並べ方の総数$n!$に閉める$a_n$の割合を$p_n$で表す。
例えば、$a_1=0,p_1=0,a_2=1,p_2=\dfrac{1}{2},$
$a_3=2,p_3=\dfrac{1}{3}$である。
(1)$a_4$の値を求めよ。
(2)$n\geqq 3$のとき、$a_n$を$a_{n-1}$と
$a_{n-2}$を用いて表せ。
(3)$n\geqq 2$のとき、$p_n-p_{n-1}$を
$n$を用いて表せ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜早稲田大学理工学部2025第2問〜領域に含まれる三角形の面積の最大値
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜早稲田大学理工学部2025第1問〜複素数平面上の点の軌跡と面積
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
複素数平面上で、複素数$z$が円$\vert z \vert=1$の上の点を動くとき、
$w=\left(\dfrac{1+\sqrt2}{2}\right)z+\left(\dfrac{1-\sqrt2}{2}\right)\dfrac{1}{z}$
を満たす点$w$の軌跡を$C$とする。
次の問いに答えよ。
(1)$C$はどのような図形か。複素数平面上に図示せよ。
(2)$C$と円$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert =\sqrt2$の共有点を求めよ。
(3)$C$で囲まれる領域と$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert \leqq \sqrt2$の
表す領域の共通部分の面積を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{1}$
複素数平面上で、複素数$z$が円$\vert z \vert=1$の上の点を動くとき、
$w=\left(\dfrac{1+\sqrt2}{2}\right)z+\left(\dfrac{1-\sqrt2}{2}\right)\dfrac{1}{z}$
を満たす点$w$の軌跡を$C$とする。
次の問いに答えよ。
(1)$C$はどのような図形か。複素数平面上に図示せよ。
(2)$C$と円$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert =\sqrt2$の共有点を求めよ。
(3)$C$で囲まれる領域と$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert \leqq \sqrt2$の
表す領域の共通部分の面積を求めよ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜慶應義塾大学理工学部2025第3問〜確率漸化式
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
点$P, Q$を数直線の原点におき、
$1$個のさいころを投げて
出た目に応じて$P, Q$を動かす。
偶数の目が出たときは$P$を正の向きに$1$だけ動かし、
$5$または$6$の目が出たときは
$Q$を正の向きに$1$だけ動かす。
たとえば、$6$の目が出たときは$P, Q$をともに
正の向きに$1$だけ動かす。
$P$と$Q$の距離が初めて$2$となるまで
さいころを投げ続けることとし、
$P$と$Q$の距離が$2$となったら、
それ以降はさいころを投げない。
$n$回さいころを投げて$P$と$Q$の距離が
$2$となる確率を$p_n$とする。
(1)$P_2 = \boxed{シ}$である。
(2)$n$回さいころを投げて、
$P$が$Q$よりも正の向きに
$1$だけ進んでいる確率を$x_n$、
$P$と$Q$が同じ位置にある確率を$y_n$、
$Q$が$P$よりも正の向きに$1$だけ進んでいる確率を
$z_n$とすると、
$y_{n+1}=\boxed{ス}x_n+\boxed{セ}y_n+\boxed{ソ}z_n$
という関係式が成立する。
また、$x_n=\boxed{タ}z_n$が成り立つ。
ただし、$\boxed{ス}$～$\boxed{タ}$には数を記入すること。
(3)関係式
$z_{n+1}+\alpha y_{n+1}=\beta(z_n+\alpha y_n)$
を満たす定数の組$(\alpha,\beta)$は$\boxed{チ}$と$\boxed{ツ}$の$2$組ある。
(4)$p_n$を$n$を用いて表すと$p_n=\boxed{テ}$となる。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{3}$
点$P, Q$を数直線の原点におき、
$1$個のさいころを投げて
出た目に応じて$P, Q$を動かす。
偶数の目が出たときは$P$を正の向きに$1$だけ動かし、
$5$または$6$の目が出たときは
$Q$を正の向きに$1$だけ動かす。
たとえば、$6$の目が出たときは$P, Q$をともに
正の向きに$1$だけ動かす。
$P$と$Q$の距離が初めて$2$となるまで
さいころを投げ続けることとし、
$P$と$Q$の距離が$2$となったら、
それ以降はさいころを投げない。
$n$回さいころを投げて$P$と$Q$の距離が
$2$となる確率を$p_n$とする。
(1)$P_2 = \boxed{シ}$である。
(2)$n$回さいころを投げて、
$P$が$Q$よりも正の向きに
$1$だけ進んでいる確率を$x_n$、
$P$と$Q$が同じ位置にある確率を$y_n$、
$Q$が$P$よりも正の向きに$1$だけ進んでいる確率を
$z_n$とすると、
$y_{n+1}=\boxed{ス}x_n+\boxed{セ}y_n+\boxed{ソ}z_n$
という関係式が成立する。
また、$x_n=\boxed{タ}z_n$が成り立つ。
ただし、$\boxed{ス}$～$\boxed{タ}$には数を記入すること。
(3)関係式
$z_{n+1}+\alpha y_{n+1}=\beta(z_n+\alpha y_n)$
を満たす定数の組$(\alpha,\beta)$は$\boxed{チ}$と$\boxed{ツ}$の$2$組ある。
(4)$p_n$を$n$を用いて表すと$p_n=\boxed{テ}$となる。
$2025$年慶應義塾大学理工学部過去問題
福田の数学〜慶應義塾大学理工学部2025第2問〜分数関数の接線とベクトル計算
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
座標平面上の点$P(1,1)$と点$Q(1,-1)$および
曲線$C:y=\dfrac{1}{x-4}(x\gt 4)$を考える。
(1)曲線$C$の接線で点$Q$を通るものは存在しないことを
証明しなさい。
(2)曲線$C$の接線で点$P$を通るものを$l$とし、
$C$と$l$の接点を$A$とする。
このとき、$l$の方程式は$y=\boxed{キ}$であり、
点$A$の座標は$\boxed{ク}$である。
また、曲線$C$上の点の点$B$が
$\overrightarrow{PB}･\overrightarrow{PA}+\overrightarrow{PA}･\overrightarrow{AQ}+\overrightarrow{AB}･\overrightarrow{AQ}=-\dfrac{2}{3}$
を満たすとき、点$B$の座標は$\boxed{ケ}$である。
(3)$A,B$を(2)で定めた点とする。
正の数$t$に対し、曲線$C$上の点$R\left(t+4,\dfrac{1}{t}\right)$は
点$A$と異なるものとする。
線分$AR$を$2:1$に内分する点を$S$とし、
線分$BS$を$3:2$に内分する点を$T(u,v)$とするとき、
$u$を$t$の式で表すと$u=\boxed{コ}$である。
また、$uv$の値は$t-\boxed{サ}$のとき最小となる。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{2}$
座標平面上の点$P(1,1)$と点$Q(1,-1)$および
曲線$C:y=\dfrac{1}{x-4}(x\gt 4)$を考える。
(1)曲線$C$の接線で点$Q$を通るものは存在しないことを
証明しなさい。
(2)曲線$C$の接線で点$P$を通るものを$l$とし、
$C$と$l$の接点を$A$とする。
このとき、$l$の方程式は$y=\boxed{キ}$であり、
点$A$の座標は$\boxed{ク}$である。
また、曲線$C$上の点の点$B$が
$\overrightarrow{PB}･\overrightarrow{PA}+\overrightarrow{PA}･\overrightarrow{AQ}+\overrightarrow{AB}･\overrightarrow{AQ}=-\dfrac{2}{3}$
を満たすとき、点$B$の座標は$\boxed{ケ}$である。
(3)$A,B$を(2)で定めた点とする。
正の数$t$に対し、曲線$C$上の点$R\left(t+4,\dfrac{1}{t}\right)$は
点$A$と異なるものとする。
線分$AR$を$2:1$に内分する点を$S$とし、
線分$BS$を$3:2$に内分する点を$T(u,v)$とするとき、
$u$を$t$の式で表すと$u=\boxed{コ}$である。
また、$uv$の値は$t-\boxed{サ}$のとき最小となる。
$2025$年慶應義塾大学理工学部過去問題
福田の数学〜慶應義塾大学理工学部2025第1問(3)〜逆関数の微分
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)$f(x)$を微分可能な関数とし、
$g(x)=x^3+x$とする。
関数$g(x)$は微分可能な逆関数$g^{-1}(x)$をもつ。
定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f'(t)$を$t$の多項式で表すと$f'(t)=\boxed{オ}$となる。
次に、任意の定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f(0)=-2$ならば$f(1)=\boxed{カ}$である。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{1}$
(3)$f(x)$を微分可能な関数とし、
$g(x)=x^3+x$とする。
関数$g(x)$は微分可能な逆関数$g^{-1}(x)$をもつ。
定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f'(t)$を$t$の多項式で表すと$f'(t)=\boxed{オ}$となる。
次に、任意の定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f(0)=-2$ならば$f(1)=\boxed{カ}$である。
$2025$年慶應義塾大学理工学部過去問題
福田の数学〜慶應義塾大学理工学部2025第1問(2)〜6または8または9で割り切れる数の個数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)$n$を自然数とする。
$1$から$n$までの自然数の中で$6$または$8$または
$9$で割り切れるものの個数を$a_n$で表す。
このとき、$a_{30}=\boxed{ウ}$となる。
また、$a_n=1000$を満たす最大の$n$は$\boxed{エ}$である。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{1}$
(2)$n$を自然数とする。
$1$から$n$までの自然数の中で$6$または$8$または
$9$で割り切れるものの個数を$a_n$で表す。
このとき、$a_{30}=\boxed{ウ}$となる。
また、$a_n=1000$を満たす最大の$n$は$\boxed{エ}$である。
$2025$年慶應義塾大学理工学部過去問題
福田の数学〜慶應義塾大学理工学部2025第1問(1)〜複素数平面上の点の軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)複素数平面上で、方程式
$\vert z+i \vert = 2 \vert z-\sqrt3 \vert$
を満たす点$z$全体が表す図形は、
中心が$\boxed{ア}$,半径が$\boxed{イ}$である。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{1}$
(1)複素数平面上で、方程式
$\vert z+i \vert = 2 \vert z-\sqrt3 \vert$
を満たす点$z$全体が表す図形は、
中心が$\boxed{ア}$,半径が$\boxed{イ}$である。
$2025$年慶應義塾大学理工学部過去問題
福田の数学〜慶應義塾大学薬学部2025第4問〜確率と期待値と無限級数
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
当たりくじが$3$本入っている$9$本のくじがある。
このくじを無作為に$1$本引き、
当たりくじかどうかを確認してから元に戻す試行を、
当たりくじが出るまで繰り返す。
当たりくじが出たときのみ得点を得ることができ、
$n$回目にの試行で当たりくじが出た場合、
得られる得点は$50n$点とする。
$n$回目に得られる得点の期待値を$E_n$とする。
ただし、$n$は自然数とする。
(1)$5$回目までに当たりくじが出る確率は$\boxed{ノ}$である。
(2)$\dfrac{E_n}{E_{n+1}}=\dfrac{10}{7}$であるとき、$n=\boxed{ハ}$である。
(3)$\displaystyle \lim_{n\to\infty}\dfrac{E_n}{E_{n+1}}$を求めると$\boxed{ヒ}$である。
(4)$\displaystyle \sum_{k=1}^{n}E_k$を$n$の式で表すと$\boxed{フ}$であり、
$\displaystyle \sum_{k=1}^{\infty}E_k$を求めると$\boxed{ヘ}$である。
ただし、$\vert r \vert \lt 1$を満たす実数$r$に対し、
$\displaystyle \lim_{n\to\infty}n \times r^n=0$が
成り立つこととする。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{4}$
当たりくじが$3$本入っている$9$本のくじがある。
このくじを無作為に$1$本引き、
当たりくじかどうかを確認してから元に戻す試行を、
当たりくじが出るまで繰り返す。
当たりくじが出たときのみ得点を得ることができ、
$n$回目にの試行で当たりくじが出た場合、
得られる得点は$50n$点とする。
$n$回目に得られる得点の期待値を$E_n$とする。
ただし、$n$は自然数とする。
(1)$5$回目までに当たりくじが出る確率は$\boxed{ノ}$である。
(2)$\dfrac{E_n}{E_{n+1}}=\dfrac{10}{7}$であるとき、$n=\boxed{ハ}$である。
(3)$\displaystyle \lim_{n\to\infty}\dfrac{E_n}{E_{n+1}}$を求めると$\boxed{ヒ}$である。
(4)$\displaystyle \sum_{k=1}^{n}E_k$を$n$の式で表すと$\boxed{フ}$であり、
$\displaystyle \sum_{k=1}^{\infty}E_k$を求めると$\boxed{ヘ}$である。
ただし、$\vert r \vert \lt 1$を満たす実数$r$に対し、
$\displaystyle \lim_{n\to\infty}n \times r^n=0$が
成り立つこととする。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜慶應義塾大学薬学部2025第3問〜逆関数と定積分
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜慶應義塾大学薬学部2025第2問〜薬の効果を検定する
単元：
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#学校別大学入試過去問解説(数学)#標本調査#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
薬を病気にかかっている患者に投与すると、
投与された患者のうちの$40$% に治療の効果が認められる。
この薬に対し、新しく開発した薬$\beta$の方が
治療の効果が認められる割合が高いかどうか、
有意水準$5$%で検定を行う。
病気$X$にかかっている患者から無作為に抽出した$1000$人に
薬を投与したとき、
$n$人以上に治療の効果が認められると、
薬$\alpha$よりも薬$\beta$の方が効果が認められる割合が高いと判断される。
ただし、薬の治療効果の標本比率を$R$、母比率を$p$とする。
(1) 帰無仮説$H_0$と対立仮説$H_1$に設定する式は
$H_0:\boxed{チ},H_1:\boxed{ツ}$である。
$H_0$が正しいと仮定するとき、
$R$は近似的に正規分布$N(\boxed{テ},\boxed{ト})$に従う。
(2) (1) をふまえ、
$n$のとりうる最小の値を求めなさい。
ただし、解答に
「標準正規分布」と「棄却域」という言葉を含めなさい。
なお、
$\sqrt{2}=1.4,\sqrt3=1.7,\sqrt5 = 2.2$として計算し、
必要に応じて正規分布表を用いなさい。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{2}$
薬を病気にかかっている患者に投与すると、
投与された患者のうちの$40$% に治療の効果が認められる。
この薬に対し、新しく開発した薬$\beta$の方が
治療の効果が認められる割合が高いかどうか、
有意水準$5$%で検定を行う。
病気$X$にかかっている患者から無作為に抽出した$1000$人に
薬を投与したとき、
$n$人以上に治療の効果が認められると、
薬$\alpha$よりも薬$\beta$の方が効果が認められる割合が高いと判断される。
ただし、薬の治療効果の標本比率を$R$、母比率を$p$とする。
(1) 帰無仮説$H_0$と対立仮説$H_1$に設定する式は
$H_0:\boxed{チ},H_1:\boxed{ツ}$である。
$H_0$が正しいと仮定するとき、
$R$は近似的に正規分布$N(\boxed{テ},\boxed{ト})$に従う。
(2) (1) をふまえ、
$n$のとりうる最小の値を求めなさい。
ただし、解答に
「標準正規分布」と「棄却域」という言葉を含めなさい。
なお、
$\sqrt{2}=1.4,\sqrt3=1.7,\sqrt5 = 2.2$として計算し、
必要に応じて正規分布表を用いなさい。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜慶應義塾大学薬学部2025第1問(5)〜複素数平面上の正n角形の頂点に関する性質
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(5)$n$は$n\geqq 3$を満たす自然数とする。
複素数$z$を$\cos\dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とおき、
複素数平面において$z^k (0\leqq k \leqq n-1)$が表す点を
$P_k$とする。
ただし、$k$は整数、$i$は虚数単位とする。
(i)$n$個の点$P_0,P_1,P_2,\cdots P_{n-1}$を
頂点とする正$n$角形の面積を$S_n$とする。
$S_n$を$n$の式で表すと$S_n=\boxed{シ}$であり、
$\displaystyle \lim_{n\to\infty}S_n$を求めると$\boxed{ス}$である。
(ii)$\displaystyle \sum_{k=1}^{n-1} z^k$を求めると$\boxed{ス}$である。
(iii)$n=7$とする。
三角形$P_1P_2P_4$の重心を$A(\alpha)$、
三角形$P_3P_5P_6$の重心を$B(\beta)$とおく。
複素数$\alpha,\beta$を求めると、
$\alpha=\boxed{ソ},\beta=\boxed{タ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(5)$n$は$n\geqq 3$を満たす自然数とする。
複素数$z$を$\cos\dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とおき、
複素数平面において$z^k (0\leqq k \leqq n-1)$が表す点を
$P_k$とする。
ただし、$k$は整数、$i$は虚数単位とする。
(i)$n$個の点$P_0,P_1,P_2,\cdots P_{n-1}$を
頂点とする正$n$角形の面積を$S_n$とする。
$S_n$を$n$の式で表すと$S_n=\boxed{シ}$であり、
$\displaystyle \lim_{n\to\infty}S_n$を求めると$\boxed{ス}$である。
(ii)$\displaystyle \sum_{k=1}^{n-1} z^k$を求めると$\boxed{ス}$である。
(iii)$n=7$とする。
三角形$P_1P_2P_4$の重心を$A(\alpha)$、
三角形$P_3P_5P_6$の重心を$B(\beta)$とおく。
複素数$\alpha,\beta$を求めると、
$\alpha=\boxed{ソ},\beta=\boxed{タ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜慶應義塾大学薬学部2025第1問(4)〜円柱を切ってできる立体の体積と側面積
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立体図形#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)$xyz$空間において、
$xy$平面上に$(0,0,0)$を中心とする半径$2$の円がある。
この円と、$(0,0,2\sqrt3)$を中心とする半径$2$の円を
底面とする円柱を、
原点を通り$xz$平面と$30$度の角をなす平面によって
切断し、$2$つの立体に分ける。
いま$2$つの立体のうち、
体積の小さい方の立体について考える。
その立体の体積を$V$、切り口の面積を$S_1$、
円柱の側面であった部分の面積を$S_2$とする。
(i)$V=\boxed{ケ}$
(ii)$S_1=\boxed{コ},S_2=\boxed{サ}$である。
この動画を見る
$\boxed{1}$
(4)$xyz$空間において、
$xy$平面上に$(0,0,0)$を中心とする半径$2$の円がある。
この円と、$(0,0,2\sqrt3)$を中心とする半径$2$の円を
底面とする円柱を、
原点を通り$xz$平面と$30$度の角をなす平面によって
切断し、$2$つの立体に分ける。
いま$2$つの立体のうち、
体積の小さい方の立体について考える。
その立体の体積を$V$、切り口の面積を$S_1$、
円柱の側面であった部分の面積を$S_2$とする。
(i)$V=\boxed{ケ}$
(ii)$S_1=\boxed{コ},S_2=\boxed{サ}$である。
福田の数学〜慶應義塾大学薬学部2025第1問(3)〜絶対値の付いた対数関数の最小
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)実数$x$に対して、関数
$f(x)=\left \vert \dfrac{1}{10^{-x}\log 10^{-x}}\right \vert$
は、$x=\boxed{キ}$のとき最小値$\boxed{ク}$をとる。
ただし、$x$は$x\gt 0$を満たし、対数は自然対数とする。
なお、$\log 2=0.69,\log 3=1.10,\log 5=1.61,$
自然対数の底$e$は$2.72$として計算し、
$\boxed{キ}$と$\boxed{ク}$は小数で答えなさい。
値が小数第$2$位までで割り切れない場合は、
小数第$3$位を四捨五入して小数第$2$位まで求めなさい。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(3)実数$x$に対して、関数
$f(x)=\left \vert \dfrac{1}{10^{-x}\log 10^{-x}}\right \vert$
は、$x=\boxed{キ}$のとき最小値$\boxed{ク}$をとる。
ただし、$x$は$x\gt 0$を満たし、対数は自然対数とする。
なお、$\log 2=0.69,\log 3=1.10,\log 5=1.61,$
自然対数の底$e$は$2.72$として計算し、
$\boxed{キ}$と$\boxed{ク}$は小数で答えなさい。
値が小数第$2$位までで割り切れない場合は、
小数第$3$位を四捨五入して小数第$2$位まで求めなさい。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜慶應義塾大学薬学部2025第1問(2)〜正八面体に内接する立方体の体積
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#立体図形#立体切断#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜慶應義塾大学薬学部2025第1問(1)〜絶対不等式と2次関数の最大最小
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$a$を実数とする。
$x$の$2$次関数$f(x)＝x^2-ax+a+2$は、
すべての実数$x$に対して$f(x)\geqq 0$を満たす。
(i)$a$の値の範囲は$\boxed{ア}$である。
(ii)$-2\leqq x\leqq 3$において、$f(x)$の最大値を$m$,
最大値を$M$とおく。
$m$が最大となるのは$a=\boxed{イ}$のときであり、
このとき$m=\boxed{ウ},M=\boxed{エ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(1)$a$を実数とする。
$x$の$2$次関数$f(x)＝x^2-ax+a+2$は、
すべての実数$x$に対して$f(x)\geqq 0$を満たす。
(i)$a$の値の範囲は$\boxed{ア}$である。
(ii)$-2\leqq x\leqq 3$において、$f(x)$の最大値を$m$,
最大値を$M$とおく。
$m$が最大となるのは$a=\boxed{イ}$のときであり、
このとき$m=\boxed{ウ},M=\boxed{エ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜東北大学2025文系第4問〜2曲線で囲まれた2つの図形の面積が等しくなる条件
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$k$を正の実数とする。
曲線$y=x(x-2)^2$と
放物線$y=kx^2$で囲まれた$2$つの
部分の面積が等しくなるような
$k$の値を求めよ。
$2025$年東北大学文系過去問題
この動画を見る
$\boxed{4}$
$k$を正の実数とする。
曲線$y=x(x-2)^2$と
放物線$y=kx^2$で囲まれた$2$つの
部分の面積が等しくなるような
$k$の値を求めよ。
$2025$年東北大学文系過去問題
藤川天が東大理三に受かった塾講師役【これが新バイトだったのか】
単元：
#大学入試過去問(数学)#物理#学校別大学入試過去問解説(数学)#大学入試過去問(物理)#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#東京大学#数学(高校生)#理科(高校生)#東京大学#東京大学
指導講師：
Morite2 English Channel
問題文全文(内容文)：
「東大理三の塾講師役」隠された真の目的が判明！
この動画を見る
「東大理三の塾講師役」隠された真の目的が判明！
福田の数学〜東北大学2025文系第3問〜四面体を拡張した四角錐の位置ベクトル
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
四面体$OABC$において、
$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$とする。
点$D$は
$\overrightarrow{AD}=3\overrightarrow{AB}+2\overrightarrow{AC}$を満たすとする。
このとき、以下の問いに答えよ。
(1)四面体$OABC$の体積を$V$とするとき、
四角錐$OABDC$の体積を$V$を用いて表せ。
(2)$\overrightarrow{OD}$を$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$で表せ。
(3)線分$AD$と線分$BC$の交点を$P$とするとき、
$\overrightarrow{OP}$を$\overrightarrow{b},\overrightarrow{c}$を用いて表せ。
(4)四面体$OABC$が$1$辺の長さ$1$の正四面体であるとき、
線分$OD$の長さを求めよ。
$2025$年東北大学文系過去問題
この動画を見る
$\boxed{3}$
四面体$OABC$において、
$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$とする。
点$D$は
$\overrightarrow{AD}=3\overrightarrow{AB}+2\overrightarrow{AC}$を満たすとする。
このとき、以下の問いに答えよ。
(1)四面体$OABC$の体積を$V$とするとき、
四角錐$OABDC$の体積を$V$を用いて表せ。
(2)$\overrightarrow{OD}$を$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$で表せ。
(3)線分$AD$と線分$BC$の交点を$P$とするとき、
$\overrightarrow{OP}$を$\overrightarrow{b},\overrightarrow{c}$を用いて表せ。
(4)四面体$OABC$が$1$辺の長さ$1$の正四面体であるとき、
線分$OD$の長さを求めよ。
$2025$年東北大学文系過去問題
福田の数学〜東北大学2025理系第6問〜2つの正五角形の重なった図形の周の長さの最小値
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{6}$
$1$辺の長さが$1$の正五角形を$K$とする。
このとき、以下の問いに答えよ。
(1)$K$の対角線の長さを求めよ。
(2)$K$の周で囲まれた図形を$P$とする。
また、$P$を$K$の外接円の中心の周りに
角$\theta$だけ回転して得られる図形を$P_{\theta}$とする。
$P$と$P_{\theta}$の共通部分の周の長さを
$\ell_{\theta}$とする。
$\theta$が$0°\lt 72°$の範囲を動くとき、
$\ell_{\theta}$の最小値が$2\sqrt5$であることを示せ。
$2025$年東北大学理系過去問題
この動画を見る
$\boxed{6}$
$1$辺の長さが$1$の正五角形を$K$とする。
このとき、以下の問いに答えよ。
(1)$K$の対角線の長さを求めよ。
(2)$K$の周で囲まれた図形を$P$とする。
また、$P$を$K$の外接円の中心の周りに
角$\theta$だけ回転して得られる図形を$P_{\theta}$とする。
$P$と$P_{\theta}$の共通部分の周の長さを
$\ell_{\theta}$とする。
$\theta$が$0°\lt 72°$の範囲を動くとき、
$\ell_{\theta}$の最小値が$2\sqrt5$であることを示せ。
$2025$年東北大学理系過去問題
【速報】東京大学が新学部を設立 #shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#東京大学#数学(高校生)#東京大学
指導講師：
Morite2 English Channel
問題文全文(内容文)：
【東大速報】70年ぶり！2027年秋に**新学部「College of Design」**を設立！全寮制・授業は全て英語・初の外国人学部長が誕生
この動画を見る
【東大速報】70年ぶり！2027年秋に**新学部「College of Design」**を設立！全寮制・授業は全て英語・初の外国人学部長が誕生
福田の数学〜東北大学2025理系第5問〜球面上の点と軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$S$を$xyz$空間内の原点$O(0,0,0)$を中心とする
半径$1$の球面とする。
また、点$P(a,b,c)$を
点$(0,0,1)$とは異なる球面$S$上の点とする。
点$P$と点$N$を通る直線$\ell$と$xy$平面との
交点を$Q$とおく。
このとき、以下の問いに答えよ。
(1)点$Q$の座標を$a,b,c$を用いて表せ。
(2)$xy$平面上の点$(p,q,0)$と点$N$を通る直線を
$m$とする。
直線$m$と球面$S$の交点のうち、
点$N$以外の交点の座標を$p,q$を用いて表せ。
(3)点$\left(0,0,\dfrac{1}{2}\right)$を通り、
ベクトル$(3,4,5)$に直交する
平面$\alpha$を考える。
点$P$が平面$\alpha$ト球面$S$との交わりを動くとき、
点$Q$は$xy$平面上の円周上を動くことを示せ。
$2025$年東北大学理系過去問題
この動画を見る
$\boxed{5}$
$S$を$xyz$空間内の原点$O(0,0,0)$を中心とする
半径$1$の球面とする。
また、点$P(a,b,c)$を
点$(0,0,1)$とは異なる球面$S$上の点とする。
点$P$と点$N$を通る直線$\ell$と$xy$平面との
交点を$Q$とおく。
このとき、以下の問いに答えよ。
(1)点$Q$の座標を$a,b,c$を用いて表せ。
(2)$xy$平面上の点$(p,q,0)$と点$N$を通る直線を
$m$とする。
直線$m$と球面$S$の交点のうち、
点$N$以外の交点の座標を$p,q$を用いて表せ。
(3)点$\left(0,0,\dfrac{1}{2}\right)$を通り、
ベクトル$(3,4,5)$に直交する
平面$\alpha$を考える。
点$P$が平面$\alpha$ト球面$S$との交わりを動くとき、
点$Q$は$xy$平面上の円周上を動くことを示せ。
$2025$年東北大学理系過去問題