 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜一橋大学2023年文系第4問〜群数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
大学入試問題#549「解き方は色々」 島根大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1}dx$
出典:2023年島根大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1}dx$
出典:2023年島根大学 入試問題
産業医科大 三角比の計算

単元:
#数Ⅰ#大学入試過去問(数学)#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#産業医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
この動画を見る
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
福田の数学〜一橋大学2023年文系第3問〜ベクトルと四面体の体積の最大

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
大学入試問題#548「結局は定石通り」 広島大学AO(2022) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
0 \lt a \lt b \lt c \\
\displaystyle \frac{1}{ab}+\displaystyle \frac{1}{bc}+\displaystyle \frac{1}{ca}=\displaystyle \frac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を満たす整数の組$(a,b,c)$をすべて求めよ。
出典:2022年広島大学AO入試
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
0 \lt a \lt b \lt c \\
\displaystyle \frac{1}{ab}+\displaystyle \frac{1}{bc}+\displaystyle \frac{1}{ca}=\displaystyle \frac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を満たす整数の組$(a,b,c)$をすべて求めよ。
出典:2022年広島大学AO入試
早稲田大 みんな大好きBBB

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
この動画を見る
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
福田の数学〜一橋大学2023年文系第2問〜共通接線が存在する条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$:y=$x^3$+2$ax^2$ および$C_2$:y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$:y=$x^3$+2$ax^2$ および$C_2$:y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
大学入試問題#547「基本問題」 愛媛大学(2023) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#愛媛大学#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$m^2-mn-2n^2=22$を満たす自然数の組$(m,n)$をすべて求めよ
出典:2023年愛媛大学
この動画を見る
$m^2-mn-2n^2=22$を満たす自然数の組$(m,n)$をすべて求めよ
出典:2023年愛媛大学
福田の数学〜一橋大学2023年文系第1問〜コンビネーションの等式を満たす自然数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+2}C_{k+1}$=2(${}_nC_{k-1}$+${}_nC_{k+1}$)
が成り立つような整数の組(n, k)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{1}$ nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+2}C_{k+1}$=2(${}_nC_{k-1}$+${}_nC_{k+1}$)
が成り立つような整数の組(n, k)を求めよ。
2023一橋大学文系過去問
誘導がなければ素晴らしい解法も出てくるんじゃね?

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
この動画を見る
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
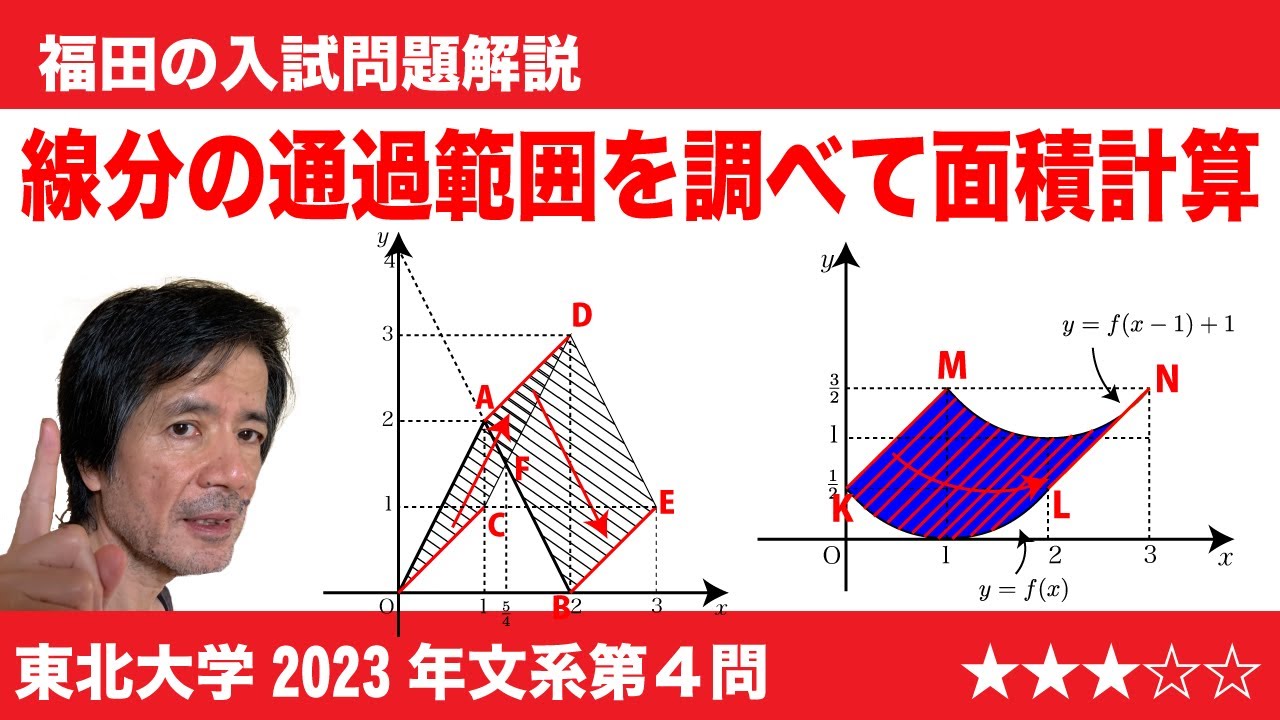
福田の数学〜東北大学2023年文系第4問〜線分の通過範囲の面積
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
大学入試問題#546「もう飽きてると思います」 愛知教育大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知教育大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2}{1+e^x} dx$
出典:2023年愛知教育大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2}{1+e^x} dx$
出典:2023年愛知教育大学 入試問題
7を書く回数?どのように考えますか?【早稲田大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
1から$10^{5}$=100000までのすべての整数を、順に十進法で書いたとすると、
数字を全部で何回書いたことになるか?答えよ.
早稲田大過去問
この動画を見る
1から$10^{5}$=100000までのすべての整数を、順に十進法で書いたとすると、
数字を全部で何回書いたことになるか?答えよ.
早稲田大過去問
大学入試だけど、中学生が解ける!?名城大

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学を数楽に
問題文全文(内容文):
$OA=OB=OC=1$
$AB=BC=CA=\sqrt 2$
四面体OABCの体積を求めよ
名城大学(改)
この動画を見る
$OA=OB=OC=1$
$AB=BC=CA=\sqrt 2$
四面体OABCの体積を求めよ
名城大学(改)
福田の数学〜東北大学2023年文系第3問〜軸の動く最大最小

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
大学入試問題#545「作成時間がありませんでした」 会津大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (2x+1)log(x+1)\ dx$
出典:2023年会津大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (2x+1)log(x+1)\ dx$
出典:2023年会津大学 入試問題
あれを使って解こう!大阪教育大

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
xを実数とする。
$x^8(y-x^2)\geqq 4$のとき、$x(x+y)\geqq 4$を示せ.
大阪教育大過去問
この動画を見る
xを実数とする。
$x^8(y-x^2)\geqq 4$のとき、$x(x+y)\geqq 4$を示せ.
大阪教育大過去問
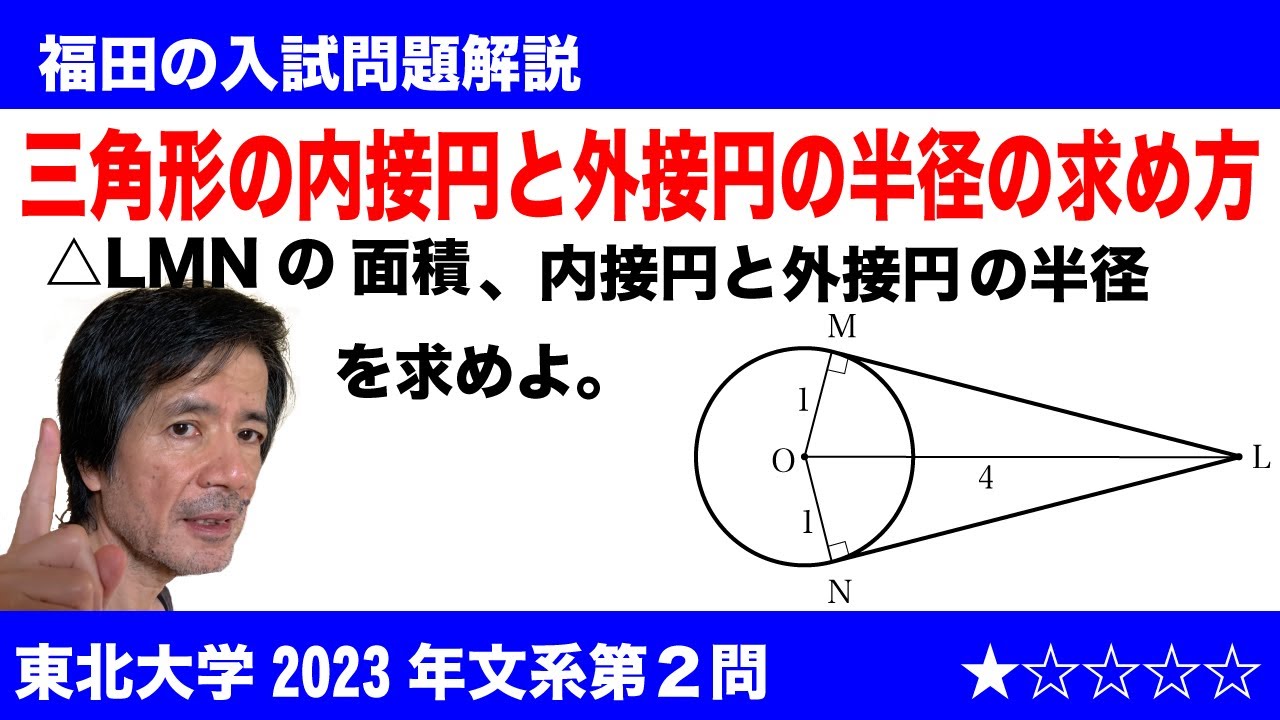
福田の数学〜東北大学2023年文系第1問〜三角形の面積と内接円と外接円の半径
単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#三角関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
大学入試問題#544「これはさすがに合同式か・・・・」 京都大学(2023) #整式

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^{2023}-1$を$x^4+x^3+x^2+x+1$で割ったときの余りを求めよ
出典:2023年京都大学 入試問題
この動画を見る
$x^{2023}-1$を$x^4+x^3+x^2+x+1$で割ったときの余りを求めよ
出典:2023年京都大学 入試問題
指数方程式の解の配置 弘前大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$4^x-2^{x+1}a+8a-15=0$の解が次の条件を満たす$a$の範囲を求めよ.
(1)ただ1つの実数解をもつとき
(2)相異なる2つの実数解がともに1以上のとき
弘前大過去問
この動画を見る
$4^x-2^{x+1}a+8a-15=0$の解が次の条件を満たす$a$の範囲を求めよ.
(1)ただ1つの実数解をもつとき
(2)相異なる2つの実数解がともに1以上のとき
弘前大過去問
福田の数学〜東北大学2023年理系第6問〜線分の通過範囲の面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#接線と法線・平均値の定理#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
大学入試問題#543「見た目は次数だけ」 前橋工科大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt[ 4 ]{ 3 }} (x^7-3x^3)e^{-\frac{x^4}{4}}\ dx$
出典:2023年前橋工科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt[ 4 ]{ 3 }} (x^7-3x^3)e^{-\frac{x^4}{4}}\ dx$
出典:2023年前橋工科大学 入試問題
二項定理 弘前大

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(1+x)^n$を展開したときの次数が奇数の項の係数の和を求めよ.
弘前大過去問
この動画を見る
$(1+x)^n$を展開したときの次数が奇数の項の係数の和を求めよ.
弘前大過去問
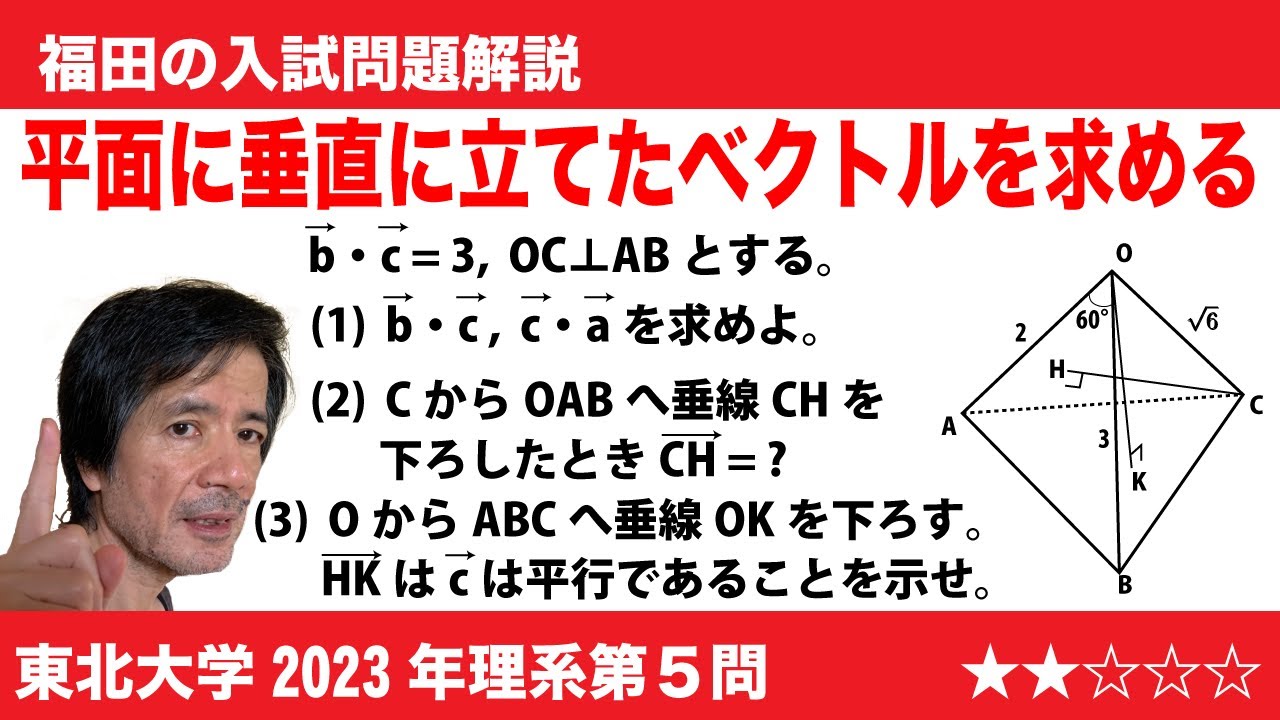
福田の数学〜東北大学2023年理系第5問〜空間ベクトルと内積
単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 四面体OABCにおいて、$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおき、次が成り立つとする。
$\angle$AOB=60°, |$\overrightarrow{a}$|=2, |$\overrightarrow{b}$|=3, |$\overrightarrow{c}$|=$\sqrt 6$, $\overrightarrow{b}$・$\overrightarrow{c}$=3
ただし、$\overrightarrow{b}$・$\overrightarrow{c}$は、2つのベクトル$\overrightarrow{b}$と$\overrightarrow{c}$の内積を表す。さらに、線分OCと線分ABは垂直であるとする。点Cから3点O, A, Bを含む平面に下ろした垂線をCHとし、点Oから3点A, B, Cを含む平面に下ろした垂線をOKとする。
(1)$\overrightarrow{a}$・$\overrightarrow{b}$と$\overrightarrow{c}$・$\overrightarrow{a}$を求めよ。
(2)ベクトル$\overrightarrow{OH}$を$\overrightarrow{a}$と$\overrightarrow{b}$を用いて表せ。
(3)ベクトル$\overrightarrow{c}$とベクトル$\overrightarrow{HK}$は平行であることを示せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{5}$ 四面体OABCにおいて、$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおき、次が成り立つとする。
$\angle$AOB=60°, |$\overrightarrow{a}$|=2, |$\overrightarrow{b}$|=3, |$\overrightarrow{c}$|=$\sqrt 6$, $\overrightarrow{b}$・$\overrightarrow{c}$=3
ただし、$\overrightarrow{b}$・$\overrightarrow{c}$は、2つのベクトル$\overrightarrow{b}$と$\overrightarrow{c}$の内積を表す。さらに、線分OCと線分ABは垂直であるとする。点Cから3点O, A, Bを含む平面に下ろした垂線をCHとし、点Oから3点A, B, Cを含む平面に下ろした垂線をOKとする。
(1)$\overrightarrow{a}$・$\overrightarrow{b}$と$\overrightarrow{c}$・$\overrightarrow{a}$を求めよ。
(2)ベクトル$\overrightarrow{OH}$を$\overrightarrow{a}$と$\overrightarrow{b}$を用いて表せ。
(3)ベクトル$\overrightarrow{c}$とベクトル$\overrightarrow{HK}$は平行であることを示せ。
2023東北大学理系過去問
大学入試問題#542「どこでも対称性が流行」 九州大学(2023) #高次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
ますただ
問題文全文(内容文):
$x^4-2x+3x^2-2x+1=0$を解け
出典:2023年九州大学 入試問題
この動画を見る
$x^4-2x+3x^2-2x+1=0$を解け
出典:2023年九州大学 入試問題
早稲田の恒等式!この形は〇〇したくなりますよね【早稲田大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
正の整数$m$,定数関数でない整式$P(x)$である.
$\displaystyle\int_{0}^{x} {P(t)}^m dt=P(x^3)-P(0)$
$P(x)$を求めよ.
早稲田大過去問
この動画を見る
正の整数$m$,定数関数でない整式$P(x)$である.
$\displaystyle\int_{0}^{x} {P(t)}^m dt=P(x^3)-P(0)$
$P(x)$を求めよ.
早稲田大過去問
福田の数学〜東北大学2023年理系第4問〜1の5乗根

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#複素数平面#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
大学入試問題#541「初手が大事」長崎大学(2023)定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{x^2}{x^2+(3-x)^2} dx$
出典:2023年長崎大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{x^2}{x^2+(3-x)^2} dx$
出典:2023年長崎大学 入試問題
ざ・漸化式 高知大

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(2n+2)a_n-na_{n+1}-3n-6=0$
(1)一般項$a_n$を求めよ.
(2)$\displaystyle \sum_{k=1}^n a_k$
高知大過去問
この動画を見る
$(2n+2)a_n-na_{n+1}-3n-6=0$
(1)一般項$a_n$を求めよ.
(2)$\displaystyle \sum_{k=1}^n a_k$
高知大過去問
福田の数学〜東北大学2023年理系第3問〜漸化式と数列の和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
