 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
三角関数の基礎問題です!2通りで解説【一橋大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形$ABC$において,$\angle A=60°$であるとする。
(1)$sinB+sinC$の取り得る値の範囲を求めよ。
(2)$sinBsinC$の取り得る値の範囲を求めよ。
一橋大過去問
この動画を見る
三角形$ABC$において,$\angle A=60°$であるとする。
(1)$sinB+sinC$の取り得る値の範囲を求めよ。
(2)$sinBsinC$の取り得る値の範囲を求めよ。
一橋大過去問
三角関数の基礎問題です!2通りで解説【一橋大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形ABCにおいて、$∠A=60°$のとき、
$\sin B+\sin C$と$\sin B \sin C$の取り得る値の範囲を求めよ.
一橋大過去問
この動画を見る
三角形ABCにおいて、$∠A=60°$のとき、
$\sin B+\sin C$と$\sin B \sin C$の取り得る値の範囲を求めよ.
一橋大過去問
福田の数学〜上智大学2022年理工学部第1問(3)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}\ (3)\int_0^{\frac{2}{3}\pi}x\sin2xdx=\frac{\pi}{\boxed{イ}}+$
$\frac{\boxed{ウ}}{\boxed{エ}}\sqrt{\boxed{オ}}$である。
2022上智大理工学部過去問
この動画を見る
${\large\boxed{1}}\ (3)\int_0^{\frac{2}{3}\pi}x\sin2xdx=\frac{\pi}{\boxed{イ}}+$
$\frac{\boxed{ウ}}{\boxed{エ}}\sqrt{\boxed{オ}}$である。
2022上智大理工学部過去問
大学入試問題#339「とりま部分積分じゃろ~~」 岡山県立大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{log(\cos\ x)}{\cos^2x} dx$
出典:2013年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{log(\cos\ x)}{\cos^2x} dx$
出典:2013年岡山県立大学 入試問題
福田の数学〜中央大学2022年理工学部第2問〜三角関数と2直線のなす角
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
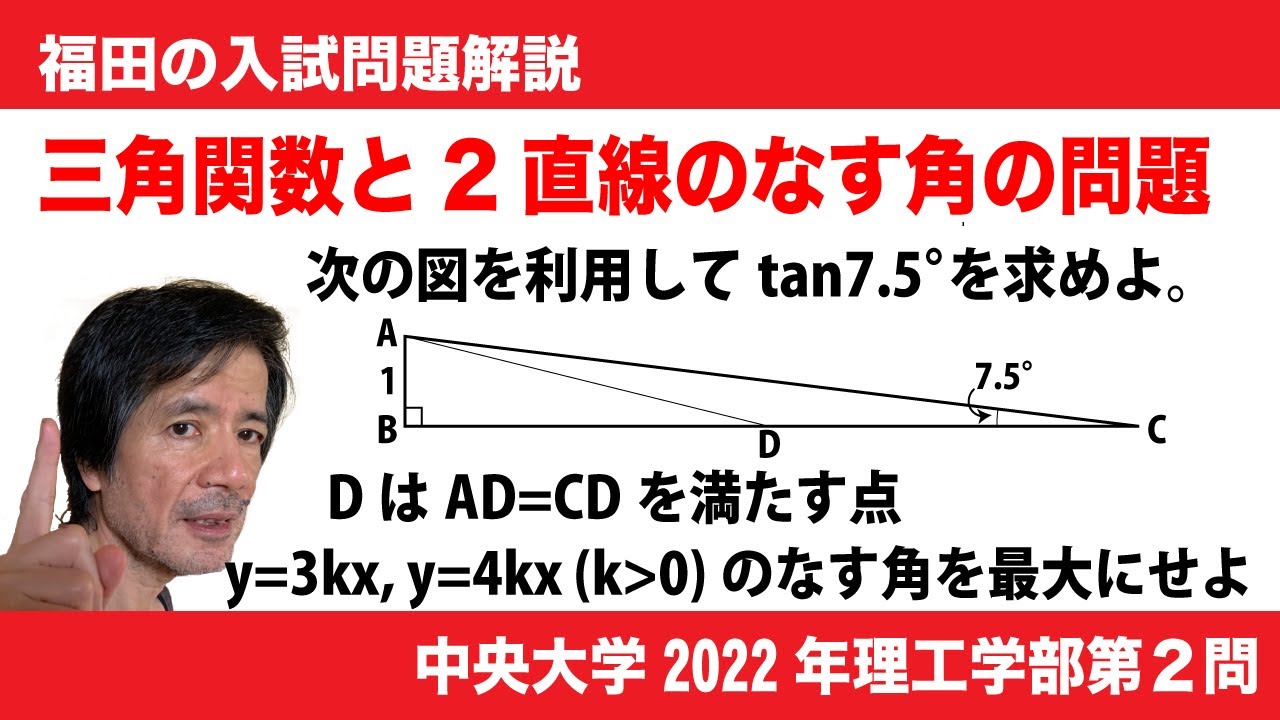
$AB = 1, \angle ABC = 90°,\angle BCA = 7.5°$である$△ABC$ の辺BC 上に $AD = CD$ と
なるように点Dをとる。このとき、$BD = \boxed{コ}, CD=\boxed{サ}$である。したがって、
$\tan 7.5° =\frac{1}{\boxed{コ}+\boxed{サ}}$
次に、正の実数kに対して、2直線$y=3kx, y = 4kx$のなす角度を$θ$とする。
だし、$0° \lt θ \lt 90°$である。このとき、$\tanθ = \boxed{シ}$である。したがって、$\tanθ$ は
$k =\frac{1}{\boxed{ス}}$ のとき最大値$\frac{1}{\boxed{セ}}$ をとる。また、$k=\frac{1}{\boxed{ス}}$ のとき$\boxed{ソ}$を満たす。
なお、必要ならば
$\sqrt2 = 1.4, \sqrt3=1.7..., \sqrt5=2.2, \sqrt6=2.4...$
を用いてよい。
$\boxed{コ},\boxed{サ}$の解答群
$ⓐ\sqrt2+\sqrt3\ \ \ ⓑ\sqrt2+\sqrt5\ \ \ ⓒ\sqrt2+\sqrt6\ \ \ ⓓ2+\sqrt3$
$ⓔ2+\sqrt5\ \ \ ⓕ2+\sqrt6\ \ \ ⓖ\sqrt3+\sqrt5\ \ \ ⓗ\sqrt5+\sqrt6$
$\boxed{シ}$の解答群
$ⓐ\frac{k}{1-12k^2}\ \ \ ⓑ\frac{k}{1+12k^2}\ \ \ ⓒ\frac{7k}{1-12k^2}\ \ \ ⓓ\frac{7k}{1+12k^2}$
$ⓔ\frac{12k^2}{1-12k^2}\ \ \ ⓕ\frac{12k^2}{1+12k^2}$
$ⓖ\frac{12k^2}{1-7k^2}\ \ \ ⓗ\frac{12k^2}{1+7k^2}$
$\boxed{ス},\boxed{セ}$の解答群
$ⓐ2\ \ \ ⓑ2\sqrt2\ \ \ ⓒ3\ \ \ ⓓ2\sqrt3\ \ \ ⓔ4\ \ \ ⓕ3\sqrt2$
$ⓖ3\sqrt3 \ \ \ ⓗ4\sqrt2 \ \ \ ⓘ6\ \ \ ⓙ4\sqrt3 \ \ \ ⓚ7\ \ \ ⓛ7\sqrt2$
$\boxed{ソ}$の解答群
$ⓐθ \gt 7.5°\ \ \ ⓑθ = 7.5°\ \ \ ⓒθ \lt 7.5°$
2022中央大学理工学部過去問
この動画を見る
$AB = 1, \angle ABC = 90°,\angle BCA = 7.5°$である$△ABC$ の辺BC 上に $AD = CD$ と
なるように点Dをとる。このとき、$BD = \boxed{コ}, CD=\boxed{サ}$である。したがって、
$\tan 7.5° =\frac{1}{\boxed{コ}+\boxed{サ}}$
次に、正の実数kに対して、2直線$y=3kx, y = 4kx$のなす角度を$θ$とする。
だし、$0° \lt θ \lt 90°$である。このとき、$\tanθ = \boxed{シ}$である。したがって、$\tanθ$ は
$k =\frac{1}{\boxed{ス}}$ のとき最大値$\frac{1}{\boxed{セ}}$ をとる。また、$k=\frac{1}{\boxed{ス}}$ のとき$\boxed{ソ}$を満たす。
なお、必要ならば
$\sqrt2 = 1.4, \sqrt3=1.7..., \sqrt5=2.2, \sqrt6=2.4...$
を用いてよい。
$\boxed{コ},\boxed{サ}$の解答群
$ⓐ\sqrt2+\sqrt3\ \ \ ⓑ\sqrt2+\sqrt5\ \ \ ⓒ\sqrt2+\sqrt6\ \ \ ⓓ2+\sqrt3$
$ⓔ2+\sqrt5\ \ \ ⓕ2+\sqrt6\ \ \ ⓖ\sqrt3+\sqrt5\ \ \ ⓗ\sqrt5+\sqrt6$
$\boxed{シ}$の解答群
$ⓐ\frac{k}{1-12k^2}\ \ \ ⓑ\frac{k}{1+12k^2}\ \ \ ⓒ\frac{7k}{1-12k^2}\ \ \ ⓓ\frac{7k}{1+12k^2}$
$ⓔ\frac{12k^2}{1-12k^2}\ \ \ ⓕ\frac{12k^2}{1+12k^2}$
$ⓖ\frac{12k^2}{1-7k^2}\ \ \ ⓗ\frac{12k^2}{1+7k^2}$
$\boxed{ス},\boxed{セ}$の解答群
$ⓐ2\ \ \ ⓑ2\sqrt2\ \ \ ⓒ3\ \ \ ⓓ2\sqrt3\ \ \ ⓔ4\ \ \ ⓕ3\sqrt2$
$ⓖ3\sqrt3 \ \ \ ⓗ4\sqrt2 \ \ \ ⓘ6\ \ \ ⓙ4\sqrt3 \ \ \ ⓚ7\ \ \ ⓛ7\sqrt2$
$\boxed{ソ}$の解答群
$ⓐθ \gt 7.5°\ \ \ ⓑθ = 7.5°\ \ \ ⓒθ \lt 7.5°$
2022中央大学理工学部過去問
福田の数学〜上智大学2022年理工学部第1問(2)〜多項定理

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)$(1+x+x^2)^{10}\ のx^{16}$の係数は$\boxed{ア}$である。
2022上智大学理工部過去問
この動画を見る
(2)$(1+x+x^2)^{10}\ のx^{16}$の係数は$\boxed{ア}$である。
2022上智大学理工部過去問
【超良問】大学入試問題#337 弘前大学(2010) #定積分 #ウォリス積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\{x(1-x)\}^{\frac{3}{2}}dx$
出典:2010年弘前大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\{x(1-x)\}^{\frac{3}{2}}dx$
出典:2010年弘前大学 入試問題
福田の数学〜上智大学2022年理工学部第1問(1)〜集合と論理

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)x,yを実数とする。次の条件を考える。
$p:xy$が無理数である.
$q:x,y$がともに無理数である.
$r:x,y$の少なくとも一方が無理数である.
$(\textrm{i})$以下から真の命題をすべて選べ。
$(\textrm{a})p \Rightarrow q\ \ \ (\textrm{b})p \Rightarrow r\ \ \ (\textrm{c})q \Rightarrow p\ \ \ (\textrm{d})q \Rightarrow r\ \ \ (\textrm{e})r \Rightarrow p\ \ \ (\textrm{f})r \Rightarrow q\ \ \ \\
(\textrm{ii})x,y$が命題「$p \Rightarrow q$」の判例であるための必要十分条件を、すべて選べ。
$(\textrm{a})$「$xy$が無理数」かつ「x,yが共に有理数」である。
$(\textrm{b})$「$xy$が有理数」かつ「x,yが共に有理数」である。
$(\textrm{c})$「$xy$が有理数」かつ「xが有理数、または、yが有理数」である。
$(\textrm{d})$「$xy$が無理数」かつ「xが有理数、または、yが有理数」である。
$(\textrm{e})$「$xy$が無理数、かつxが有理数」または「xyが無理数、かつ、yが有
理数」である。
$(\textrm{f})$「$xy$が無理数、かつxが有理数」または「xyが有理数、かつ、yが有
理数」である。
2022上智大学理工学部過去問
この動画を見る
(1)x,yを実数とする。次の条件を考える。
$p:xy$が無理数である.
$q:x,y$がともに無理数である.
$r:x,y$の少なくとも一方が無理数である.
$(\textrm{i})$以下から真の命題をすべて選べ。
$(\textrm{a})p \Rightarrow q\ \ \ (\textrm{b})p \Rightarrow r\ \ \ (\textrm{c})q \Rightarrow p\ \ \ (\textrm{d})q \Rightarrow r\ \ \ (\textrm{e})r \Rightarrow p\ \ \ (\textrm{f})r \Rightarrow q\ \ \ \\
(\textrm{ii})x,y$が命題「$p \Rightarrow q$」の判例であるための必要十分条件を、すべて選べ。
$(\textrm{a})$「$xy$が無理数」かつ「x,yが共に有理数」である。
$(\textrm{b})$「$xy$が有理数」かつ「x,yが共に有理数」である。
$(\textrm{c})$「$xy$が有理数」かつ「xが有理数、または、yが有理数」である。
$(\textrm{d})$「$xy$が無理数」かつ「xが有理数、または、yが有理数」である。
$(\textrm{e})$「$xy$が無理数、かつxが有理数」または「xyが無理数、かつ、yが有
理数」である。
$(\textrm{f})$「$xy$が無理数、かつxが有理数」または「xyが有理数、かつ、yが有
理数」である。
2022上智大学理工学部過去問
漸化式・対数の利用の融合問題 福井大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=1,a_{n+1}=\dfrac{a_n}{a_n+3},a_{11}$は小数点以下0でない数が初めて表れるのは小数第何位?
福井大過去問
この動画を見る
$ a_1=1,a_{n+1}=\dfrac{a_n}{a_n+3},a_{11}$は小数点以下0でない数が初めて表れるのは小数第何位?
福井大過去問
整数問題!これ2通りで解けますか?【札幌医科大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#札幌医科大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
自然数$n$に対して
$N=(n+2)^3-n(n+1)(n+2)$
が36の倍数になるような$n$をすべて求めよ。
札幌医科大過去問
この動画を見る
自然数$n$に対して
$N=(n+2)^3-n(n+1)(n+2)$
が36の倍数になるような$n$をすべて求めよ。
札幌医科大過去問
福田の数学〜上智大学2022年TEAP理系型第4問〜媒介変数で表された極方程式

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#上智大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、原点を極とし、x軸の正の部分を始線とする極座標を考え
る。平面上を運動する点Pの極座標$(r,\ θ)$が、時刻$t \geqq 0$の関数として、
$r=1+t,\ \ \ θ=\log(1+t)$
で与えられるとする。時刻$t=0$にPが出発してから初めてy軸上に到着するまで
にPが描く軌跡をCとする。
(1)$\ t \gt 0$において、Pが初めてy軸上に到着するときのtの値を求めよ。
(2)C上の点のx座標の最大値を求めよ。
(3)Cの長さを求めよ。
(4)Cを座標平面上に図示せよ。
(5)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2022上智大学理系過去問
この動画を見る
座標平面において、原点を極とし、x軸の正の部分を始線とする極座標を考え
る。平面上を運動する点Pの極座標$(r,\ θ)$が、時刻$t \geqq 0$の関数として、
$r=1+t,\ \ \ θ=\log(1+t)$
で与えられるとする。時刻$t=0$にPが出発してから初めてy軸上に到着するまで
にPが描く軌跡をCとする。
(1)$\ t \gt 0$において、Pが初めてy軸上に到着するときのtの値を求めよ。
(2)C上の点のx座標の最大値を求めよ。
(3)Cの長さを求めよ。
(4)Cを座標平面上に図示せよ。
(5)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2022上智大学理系過去問
大学入試問題#336 横浜国立大学2013 #定積分
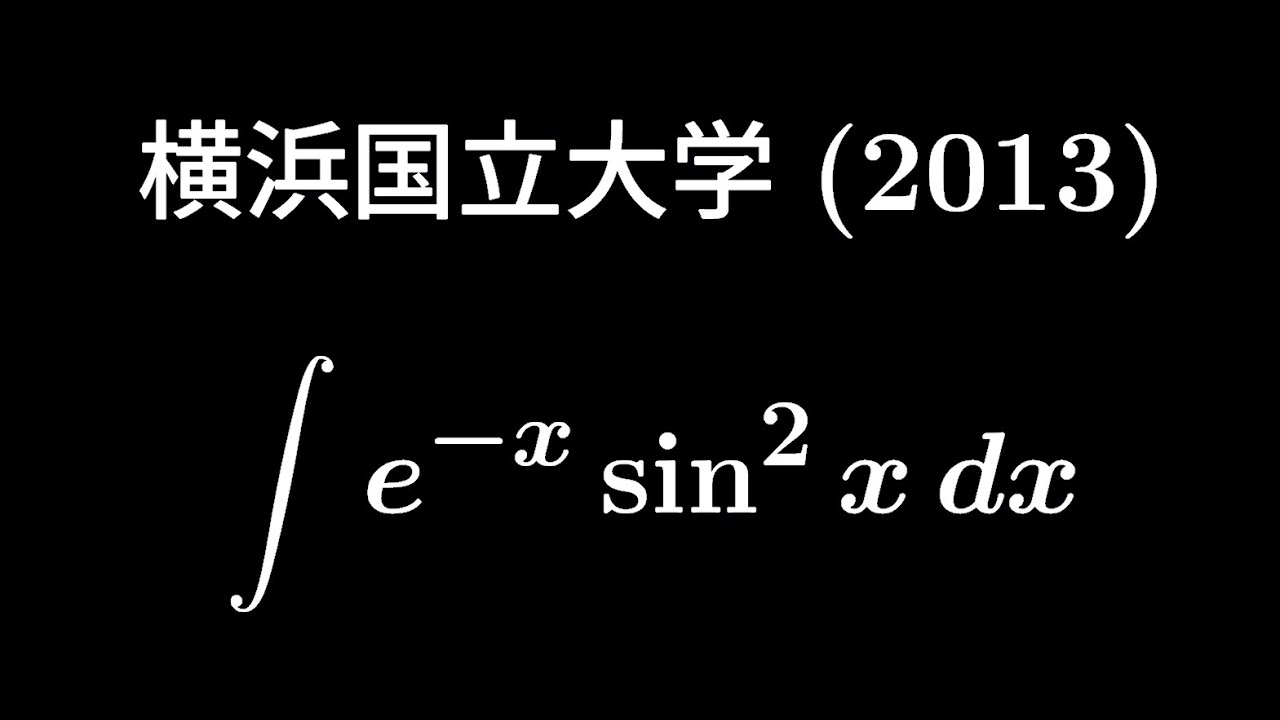
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int e^{-x}\sin^2x\ dx$
出典:2013年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int e^{-x}\sin^2x\ dx$
出典:2013年横浜国立大学 入試問題
富山大(医)整数問題基本

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$4^{3n-2}-1$を9で割ると3余ることを示せ.
(2)$n^3+3n^2+2n-3$は5の倍数でないことを示せ.
富山大(医)過去問
この動画を見る
(1)$4^{3n-2}-1$を9で割ると3余ることを示せ.
(2)$n^3+3n^2+2n-3$は5の倍数でないことを示せ.
富山大(医)過去問
福田の数学〜上智大学2022年TEAP理系型第3問〜最後の目が得点になる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#確率分布と統計的な推測#確率分布#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
各頂点に1から4までの数が1つずつ書いてあり、振るとそれらの1つが等し
い確率で得られる正四面体の形のさいころTがある。これを用いて、2人のプレイ
ヤA, B が以下のようなゲームをする。それぞれの枠内に記したルールに従い、各
プレイヤがTを1回以上振って、最後に出た数をそのプレイヤの得点とし、得点の
多い方を勝ちとする。ここで、同点のときには常にBの勝ちとする。また、振り直
すかどうかは、各プレイヤーとも自分が勝つ確率を最大にするように選択するとす
る。このとき、Aが勝つ確率pについて答えよ。ただし、以下のそれぞれの場合に
ついて、pは0以上の整数k, nを用いて$p =\frac{2k+1}{2^n}$と表せるので、このk, nを
答えよ。
(1)$A, B$がそれぞれ1回ずつTを振る
このときpを表すk, nは、$k=\boxed{ケ} ,\ n=\boxed{コ}$である。
(2)先にAが一回振る。次にBが2回まで振ってよい(Aの得点を知っている状
況で、1回振り直してよい)
このときpを表すk,nは、$k=\boxed{サ} ,\ n=\boxed{シ}$である。
(3)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが1回振る。
このときpを表すk,nは、$k=\boxed{ス} ,\ n=\boxed{セ }$である。
(4)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、1回
振り直してよい)
このときpを表すk,nは、$k=\boxed{ソ} ,\ n=\boxed{タ}$である。
(5)先にAが3回まで振ってよい(Bの得点がまだわからない状況で、2回まで振
り直してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、
1回振り直してよい)
このときpを表すk,nは、$k=\boxed{チ} ,\ n=\boxed{ツ}$である。
2022上智大学理系過去問
この動画を見る
各頂点に1から4までの数が1つずつ書いてあり、振るとそれらの1つが等し
い確率で得られる正四面体の形のさいころTがある。これを用いて、2人のプレイ
ヤA, B が以下のようなゲームをする。それぞれの枠内に記したルールに従い、各
プレイヤがTを1回以上振って、最後に出た数をそのプレイヤの得点とし、得点の
多い方を勝ちとする。ここで、同点のときには常にBの勝ちとする。また、振り直
すかどうかは、各プレイヤーとも自分が勝つ確率を最大にするように選択するとす
る。このとき、Aが勝つ確率pについて答えよ。ただし、以下のそれぞれの場合に
ついて、pは0以上の整数k, nを用いて$p =\frac{2k+1}{2^n}$と表せるので、このk, nを
答えよ。
(1)$A, B$がそれぞれ1回ずつTを振る
このときpを表すk, nは、$k=\boxed{ケ} ,\ n=\boxed{コ}$である。
(2)先にAが一回振る。次にBが2回まで振ってよい(Aの得点を知っている状
況で、1回振り直してよい)
このときpを表すk,nは、$k=\boxed{サ} ,\ n=\boxed{シ}$である。
(3)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが1回振る。
このときpを表すk,nは、$k=\boxed{ス} ,\ n=\boxed{セ }$である。
(4)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、1回
振り直してよい)
このときpを表すk,nは、$k=\boxed{ソ} ,\ n=\boxed{タ}$である。
(5)先にAが3回まで振ってよい(Bの得点がまだわからない状況で、2回まで振
り直してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、
1回振り直してよい)
このときpを表すk,nは、$k=\boxed{チ} ,\ n=\boxed{ツ}$である。
2022上智大学理系過去問
大学入試問題#335 防衛医科大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$0 \lt a \lt 1$
$\displaystyle \int_{a}^{1}x\sqrt{ 1-x }\ dx$
出典:2010年防衛医科大学 入試問題
この動画を見る
$0 \lt a \lt 1$
$\displaystyle \int_{a}^{1}x\sqrt{ 1-x }\ dx$
出典:2010年防衛医科大学 入試問題
n進法に苦手意識ある人必見!難しいことはありません【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を4以上の自然数とする。数2,12,1331がすべて$n$進法で表記されているとして,
$2^{12}=1331$
が成り立っている。このとき$n$はいくつか。十進法で答えよ。
京都大過去問
この動画を見る
$n$を4以上の自然数とする。数2,12,1331がすべて$n$進法で表記されているとして,
$2^{12}=1331$
が成り立っている。このとき$n$はいくつか。十進法で答えよ。
京都大過去問
福田の数学〜上智大学2022年TEAP理系型第2問〜空間ベクトルと軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
一辺の長さが1である立方体QACB-CFGEを考える。
$\overrightarrow{ OA } = \overrightarrow{ a },\ \overrightarrow{ OB } $
$= \overrightarrow{ b },\ \overrightarrow{ OC } = \overrightarrow{ c },$ とおき、実数s,tに対し
点P,Qを
$\overrightarrow{ OP } =(1-s)\overrightarrow{ a } +s\ \overrightarrow{ b }+$
$s\ \overrightarrow{ c },\ \ \overrightarrow{ OQ } =\overrightarrow{ a } +t\ \overrightarrow{ b }+(1-t)\ \overrightarrow{ c }$
を満たす点とする。
(1)点Pは直線$\boxed{あ}$上にあり、点Qは直線$\boxed{い}$上にある。
(2)直線$\boxed{あ}$と直線$\boxed{い}$とは$\boxed{う }$
$\boxed{う}$の選択肢
$(\textrm{a})$一致する $(\textrm{b})$平行である $(\textrm{c})$直交する $(\textrm{d})$交わるが直交しない。
$(\textrm{e})$ねじれの位置にあって垂直である $(\textrm{f})$ねじれの位置にあって垂直でない。
(3)線分PQの長さは、$s=\boxed{え},\ t=\boxed{お}$のとき最小値をとり、
このとき$PQ^2=\boxed{か}$である。
$\boxed{え}\ \boxed{お}\ \boxed{か}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{6}\ \ \ (\textrm{c})\frac{1}{4}\ \ \ (\textrm{d})\frac{1}{3}$
$(\textrm{e})\frac{1}{2}\ \ \ (\textrm{f})\frac{2}{3}\ \ \ (\textrm{g})\frac{3}{4}\ \ \ (\textrm{h})1$
$(\textrm{i})\frac{4}{3}\ \ \ (\textrm{j})\frac{3}{2}\ \ \ (\textrm{k})2\ \ \ (\textrm{l})3$
(4)$s,t$が$0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1$の範囲を動くとき、線分PQの中点Mの動く領域は
$\boxed{き}$であり、その面積は$\frac{\sqrt{\boxed{オ}}}{\boxed{カ}}$である。
$\boxed{き}$の選択肢
$(\textrm{a})$正三角形 $(\textrm{b})$直角二等辺三角形 $(\textrm{c})$直角二等辺三角形でない直角三角形
$(\textrm{d})$直角二等辺三角形でない直角三角形でもない三角形 $(\textrm{e})$正方形 $(\textrm{f})$正方形でない長方形
$(\textrm{g})$長方形でない平行四辺形 $(\textrm{h})$並行四辺形でない四角形$(\textrm{i})$五角形$(\textrm{i})$六角形
(5)$s,t$が$0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1$の範囲を動くとき、線分PQが通過する領域の体積は
$\frac{\boxed{キ}}{\boxed{ク}}$である。
2022上智大学理系過去問
この動画を見る
一辺の長さが1である立方体QACB-CFGEを考える。
$\overrightarrow{ OA } = \overrightarrow{ a },\ \overrightarrow{ OB } $
$= \overrightarrow{ b },\ \overrightarrow{ OC } = \overrightarrow{ c },$ とおき、実数s,tに対し
点P,Qを
$\overrightarrow{ OP } =(1-s)\overrightarrow{ a } +s\ \overrightarrow{ b }+$
$s\ \overrightarrow{ c },\ \ \overrightarrow{ OQ } =\overrightarrow{ a } +t\ \overrightarrow{ b }+(1-t)\ \overrightarrow{ c }$
を満たす点とする。
(1)点Pは直線$\boxed{あ}$上にあり、点Qは直線$\boxed{い}$上にある。
(2)直線$\boxed{あ}$と直線$\boxed{い}$とは$\boxed{う }$
$\boxed{う}$の選択肢
$(\textrm{a})$一致する $(\textrm{b})$平行である $(\textrm{c})$直交する $(\textrm{d})$交わるが直交しない。
$(\textrm{e})$ねじれの位置にあって垂直である $(\textrm{f})$ねじれの位置にあって垂直でない。
(3)線分PQの長さは、$s=\boxed{え},\ t=\boxed{お}$のとき最小値をとり、
このとき$PQ^2=\boxed{か}$である。
$\boxed{え}\ \boxed{お}\ \boxed{か}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{6}\ \ \ (\textrm{c})\frac{1}{4}\ \ \ (\textrm{d})\frac{1}{3}$
$(\textrm{e})\frac{1}{2}\ \ \ (\textrm{f})\frac{2}{3}\ \ \ (\textrm{g})\frac{3}{4}\ \ \ (\textrm{h})1$
$(\textrm{i})\frac{4}{3}\ \ \ (\textrm{j})\frac{3}{2}\ \ \ (\textrm{k})2\ \ \ (\textrm{l})3$
(4)$s,t$が$0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1$の範囲を動くとき、線分PQの中点Mの動く領域は
$\boxed{き}$であり、その面積は$\frac{\sqrt{\boxed{オ}}}{\boxed{カ}}$である。
$\boxed{き}$の選択肢
$(\textrm{a})$正三角形 $(\textrm{b})$直角二等辺三角形 $(\textrm{c})$直角二等辺三角形でない直角三角形
$(\textrm{d})$直角二等辺三角形でない直角三角形でもない三角形 $(\textrm{e})$正方形 $(\textrm{f})$正方形でない長方形
$(\textrm{g})$長方形でない平行四辺形 $(\textrm{h})$並行四辺形でない四角形$(\textrm{i})$五角形$(\textrm{i})$六角形
(5)$s,t$が$0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1$の範囲を動くとき、線分PQが通過する領域の体積は
$\frac{\boxed{キ}}{\boxed{ク}}$である。
2022上智大学理系過去問
【最後の足し算で計算ミスしてます。】大学入試問題#334 広島市立大学(2011) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2+1}{x+1}dx$
出典:2011年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2+1}{x+1}dx$
出典:2011年広島市立大学 入試問題
大学入試問題#333 青山学院大学(2013) #定積分 #極限

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{log\ a}\displaystyle \frac{e^x}{e^x+a}dx$
出典:2013年青山学院大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{log\ a}\displaystyle \frac{e^x}{e^x+a}dx$
出典:2013年青山学院大学 入試問題
福田の数学〜上智大学2022年TEAP理系型第1問(3)〜命題と必要十分な条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1
(3) aを正の実数とする。 実数からなる集合X, Yを次で定める。
$X={x|0 < x < a}, Y={y|3 < y < 5}$
次のそれぞれの命題が成り立つための必要十分条件を、選択肢から1つずつ選べ。
(i) すべてのx∈Xとすべてのy∈Yに対してx<yとなる
(ii) 「すべてのx∈Xに対してx<y」となるy∈Yが存在する
(iii) すべてのx∈Xに対して「x<yとなるy∈Yが存在する」
2022上智大学理系過去問
この動画を見る
1
(3) aを正の実数とする。 実数からなる集合X, Yを次で定める。
$X={x|0 < x < a}, Y={y|3 < y < 5}$
次のそれぞれの命題が成り立つための必要十分条件を、選択肢から1つずつ選べ。
(i) すべてのx∈Xとすべてのy∈Yに対してx<yとなる
(ii) 「すべてのx∈Xに対してx<y」となるy∈Yが存在する
(iii) すべてのx∈Xに対して「x<yとなるy∈Yが存在する」
2022上智大学理系過去問
福田の数学〜上智大学2022年TEAP理系型第1問(2)〜平均と分散の計算

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1(2)あるクラスの生徒は12人で、A,B,Cの3つのグループに分かれている。
Aグループは3人、Bグループは4人、Cグループは5人の生徒からなる。
このクラスでテストを行った。各人の点数は0以上10以下の整数である。
(i) A グループの生徒3人の点数の分散は6であり、そのうち2人の点数はそれぞれ2と5である。
このとき、 残りの1人の点数は[イ]である。
(ii)さらに、Bグループの生徒4人の点数の平均値は2であり、分散は3である。
Cグループの生徒5人の点数の平均値は5であり、分散は6である。
このとき、クラスの生徒12人の点数の平均値は[ウ]であり、分散は[エ]である。
2022上智大学理系過去問
この動画を見る
1(2)あるクラスの生徒は12人で、A,B,Cの3つのグループに分かれている。
Aグループは3人、Bグループは4人、Cグループは5人の生徒からなる。
このクラスでテストを行った。各人の点数は0以上10以下の整数である。
(i) A グループの生徒3人の点数の分散は6であり、そのうち2人の点数はそれぞれ2と5である。
このとき、 残りの1人の点数は[イ]である。
(ii)さらに、Bグループの生徒4人の点数の平均値は2であり、分散は3である。
Cグループの生徒5人の点数の平均値は5であり、分散は6である。
このとき、クラスの生徒12人の点数の平均値は[ウ]であり、分散は[エ]である。
2022上智大学理系過去問
整数問題の難問!誘導ありでも難しいです【九州大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
自然数$m,n$が、$n^4=1+210m^2$ ・・・①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
この動画を見る
自然数$m,n$が、$n^4=1+210m^2$ ・・・①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
福田の数学〜上智大学2022年TEAP理系型第1問(1)〜1次の近似式

単元:
#大学入試過去問(数学)#微分とその応用#学校別大学入試過去問解説(数学)#速度と近似式#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
1 (1) $\cos 61°$の近似値を求めたい。$y=\cos x$ の1次の近似式を用いて計算し、
小数第3位を四捨五入すると $\cos 61° ≒ 0. [ア] $を得る。
ただし、$\pi= 3.14 √3=1.73 $として用いてよい。
2022上智大学理系過去問
この動画を見る
1 (1) $\cos 61°$の近似値を求めたい。$y=\cos x$ の1次の近似式を用いて計算し、
小数第3位を四捨五入すると $\cos 61° ≒ 0. [ア] $を得る。
ただし、$\pi= 3.14 √3=1.73 $として用いてよい。
2022上智大学理系過去問
福岡教育大 複素平面の基本

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ z=a+bi(a \gt 0,b \gt 0)z^2+\dfrac{1}{z^2}=1$を満たす.
(1)zを極形式で表せ$(0 \lt \theta \lt 2\pi)$
(2)$z^{100}+\dfrac{1}{z^{100}}$の値を求めよ.
(3)$z,z^2,z^{100}+\dfrac{1}{z^{100}}$の三点でできる三角形の面積を求めよ.
福岡教育大過去問
この動画を見る
$ z=a+bi(a \gt 0,b \gt 0)z^2+\dfrac{1}{z^2}=1$を満たす.
(1)zを極形式で表せ$(0 \lt \theta \lt 2\pi)$
(2)$z^{100}+\dfrac{1}{z^{100}}$の値を求めよ.
(3)$z,z^2,z^{100}+\dfrac{1}{z^{100}}$の三点でできる三角形の面積を求めよ.
福岡教育大過去問
福田の数学〜上智大学2022年TEAP文系型第4問(3)〜指数不等式と領域における最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#軌跡と領域#指数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(3)正の数の組$(x,\ y)$が
$\begin{array}{1}
x \geqq 1\\
y \geqq 1\\
x^5y^4 \geqq 100\\
x^2y^9 \geqq 100\\
\end{array}$
を満たすとき$z=xy$は$(x,\ y)=(a,\ b)$で最小値をとる。ここで、
$\log_{10}a=\frac{\boxed{ヤ}}{\boxed{ユ}},\ \log_{10}b=\frac{\boxed{ヨ}}{\boxed{ワ}}$
である。
2022上智大学文系過去問
この動画を見る
(3)正の数の組$(x,\ y)$が
$\begin{array}{1}
x \geqq 1\\
y \geqq 1\\
x^5y^4 \geqq 100\\
x^2y^9 \geqq 100\\
\end{array}$
を満たすとき$z=xy$は$(x,\ y)=(a,\ b)$で最小値をとる。ここで、
$\log_{10}a=\frac{\boxed{ヤ}}{\boxed{ユ}},\ \log_{10}b=\frac{\boxed{ヨ}}{\boxed{ワ}}$
である。
2022上智大学文系過去問
大学入試問題#330 横浜国立大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\sqrt{ 1+2\sqrt{ x } }\ dx$
出典:2013年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\sqrt{ 1+2\sqrt{ x } }\ dx$
出典:2013年横浜国立大学 入試問題
宮城教育大・多項式の剰余

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P(x),Q(x)$はxの実数係数多項式である.
$P(x),Q(x)$が$x^2+1$で割り切れるなら$P(x),Q(x)$の少なくとも一方は$x^2+1$で割り切れることを証明せよ.
(1)$P(i)=0$ならば$P(x)$は$x^2+1$で割り切れることを示せ.
宮城教育大過去問
この動画を見る
$P(x),Q(x)$はxの実数係数多項式である.
$P(x),Q(x)$が$x^2+1$で割り切れるなら$P(x),Q(x)$の少なくとも一方は$x^2+1$で割り切れることを証明せよ.
(1)$P(i)=0$ならば$P(x)$は$x^2+1$で割り切れることを示せ.
宮城教育大過去問
福田の数学〜上智大学2022年TEAP文系型第4問(2)〜円が直線から切り取る線分の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)$t \gt 0$とし、xy平面上の直線
$l:y=-x+t$
と領域
$B:x^2+(y-2)^2 \leqq \frac{1}{4}t^2$
を考える。Bとlが2点以上で交わるとき、交わりとして得られる線分の長さは
$t=\boxed{ム}$のときに最大値$\boxed{メ}\sqrt{\boxed{モ}}$をとる。
2022上智大学文系過去問
この動画を見る
(2)$t \gt 0$とし、xy平面上の直線
$l:y=-x+t$
と領域
$B:x^2+(y-2)^2 \leqq \frac{1}{4}t^2$
を考える。Bとlが2点以上で交わるとき、交わりとして得られる線分の長さは
$t=\boxed{ム}$のときに最大値$\boxed{メ}\sqrt{\boxed{モ}}$をとる。
2022上智大学文系過去問
大学入試問題#329 熊本大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\displaystyle \frac{\theta}{2}}{1+\sin\displaystyle \frac{\theta}{2}}d\theta$
出典:2013年熊本大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\displaystyle \frac{\theta}{2}}{1+\sin\displaystyle \frac{\theta}{2}}d\theta$
出典:2013年熊本大学 入試問題
福田の数学〜上智大学2022年TEAP文系型第4問(1)〜必要十分条件と条件の否定

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)実数の数列${a_n}$に関する以下の条件 $(P)$ を考える。
$(P) 「n\geqq N$ならば $a_n \leqq 4$」が成り立つ自然数Nが存在する
$(\textrm{i})$ 以下の選択肢から、(P) であるための必要十分条件をすべて選べ。
$(\textrm{ii})$ 以下の選択肢から、(P) であるための必要条件ではあるが十分条件ではないもの
をすべて選べ。
$(\textrm{iii})$ 以下の選択肢から、(P) の否定であるものをすべて選べ。
選択肢$(\textrm{a})$「$n\gt N$ ならば$a_n \leqq 4$」が成り立つ自然数Nが存在する
$(\textrm{b})$ 「$n \lt N$ ならば$an \leqq 4$」 が成り立つ自然数Nが存在する
$(\textrm{c})$ 「$n\geqq N$ならば$a_n\gt 4$」 が成り立つ自然数Nが存在する
$(\textrm{d}) a_n \gt 4$ を満たす自然数n が無限個存在する
$(\textrm{e}) a_n \leqq 4$ を満たす自然数nが無限個存在する
$(\textrm{f}) a_n \gt 4$ を満たす自然数nは存在しても有限個である
$(\textrm{g}) a_n \leqq 4$ を満たす自然数nは存在しても有限個である
2022上智大学文系過去問
この動画を見る
(1)実数の数列${a_n}$に関する以下の条件 $(P)$ を考える。
$(P) 「n\geqq N$ならば $a_n \leqq 4$」が成り立つ自然数Nが存在する
$(\textrm{i})$ 以下の選択肢から、(P) であるための必要十分条件をすべて選べ。
$(\textrm{ii})$ 以下の選択肢から、(P) であるための必要条件ではあるが十分条件ではないもの
をすべて選べ。
$(\textrm{iii})$ 以下の選択肢から、(P) の否定であるものをすべて選べ。
選択肢$(\textrm{a})$「$n\gt N$ ならば$a_n \leqq 4$」が成り立つ自然数Nが存在する
$(\textrm{b})$ 「$n \lt N$ ならば$an \leqq 4$」 が成り立つ自然数Nが存在する
$(\textrm{c})$ 「$n\geqq N$ならば$a_n\gt 4$」 が成り立つ自然数Nが存在する
$(\textrm{d}) a_n \gt 4$ を満たす自然数n が無限個存在する
$(\textrm{e}) a_n \leqq 4$ を満たす自然数nが無限個存在する
$(\textrm{f}) a_n \gt 4$ を満たす自然数nは存在しても有限個である
$(\textrm{g}) a_n \leqq 4$ を満たす自然数nは存在しても有限個である
2022上智大学文系過去問
