 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜慶應義塾大学2022年総合政策学部第5問〜等脚台形の外接円の中心の位置ベクトル

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}$いま、ADを下底、BCを上底とする台形ABCDにおいて、$\angle BAD=\angle CDA=60°,$
$|\overrightarrow{ AB }|=2,|\overrightarrow{ BC }|=1$となっている。
(1)$|\overrightarrow{ BD }|=\sqrt{\boxed{\ \ アイ\ \ }}$であり、台形ABCDの外接円の半径は$\frac{\sqrt{\boxed{\ \ ウエ\ \ }}}{\boxed{\ \ オカ\ \ }}$である。
(2)外接円の中心をOとするとき、内積$\overrightarrow{ AB }・\overrightarrow{ AO }=\boxed{\ \ キク\ \ },\overrightarrow{ AD }・\overrightarrow{ AO }=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(3)$\overrightarrow{ AO }=\frac{\boxed{\ \ スセ\ \ }}{\boxed{\ \ ソタ\ \ }}\ \overrightarrow{ AB }+\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \overrightarrow{ AD }$である。
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{5}}$いま、ADを下底、BCを上底とする台形ABCDにおいて、$\angle BAD=\angle CDA=60°,$
$|\overrightarrow{ AB }|=2,|\overrightarrow{ BC }|=1$となっている。
(1)$|\overrightarrow{ BD }|=\sqrt{\boxed{\ \ アイ\ \ }}$であり、台形ABCDの外接円の半径は$\frac{\sqrt{\boxed{\ \ ウエ\ \ }}}{\boxed{\ \ オカ\ \ }}$である。
(2)外接円の中心をOとするとき、内積$\overrightarrow{ AB }・\overrightarrow{ AO }=\boxed{\ \ キク\ \ },\overrightarrow{ AD }・\overrightarrow{ AO }=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(3)$\overrightarrow{ AO }=\frac{\boxed{\ \ スセ\ \ }}{\boxed{\ \ ソタ\ \ }}\ \overrightarrow{ AB }+\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \overrightarrow{ AD }$である。
2022慶應義塾大学総合政策学部過去問
大学入試問題#247 明治大学(2014) #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ h \to 0 }\displaystyle \frac{log(1+5h+6h^2)}{h}$を求めよ。
出典:2014年明治大学 入試問題
この動画を見る
$\displaystyle \lim_{ h \to 0 }\displaystyle \frac{log(1+5h+6h^2)}{h}$を求めよ。
出典:2014年明治大学 入試問題
式の値 虚数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
3次方程式$x^3+1 = 0$の虚数解の1つをαとするとき
$α^{300} + α^{200} + α^{100} + \frac {1}{α^{100}} + \frac {1}{α^{200}} +\frac {1}{α^{300}} = ?$
甲南大学
この動画を見る
3次方程式$x^3+1 = 0$の虚数解の1つをαとするとき
$α^{300} + α^{200} + α^{100} + \frac {1}{α^{100}} + \frac {1}{α^{200}} +\frac {1}{α^{300}} = ?$
甲南大学
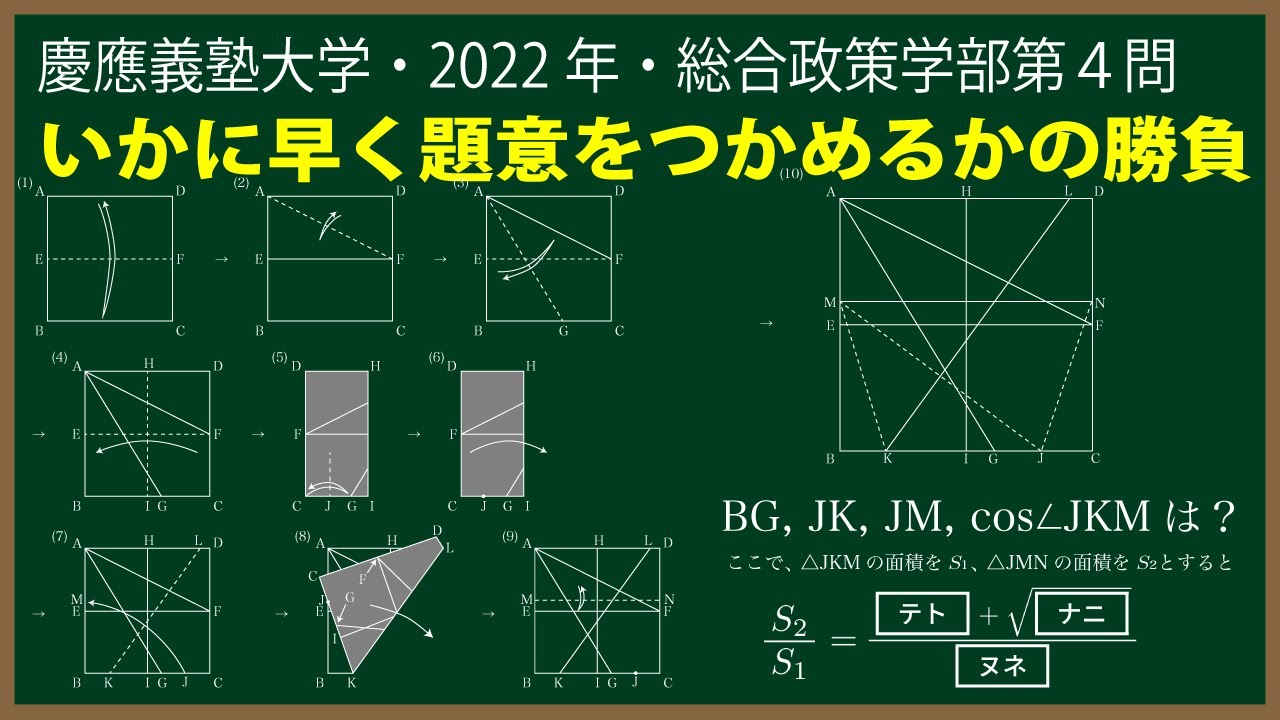
福田の数学〜慶應義塾大学2022年総合政策学部第4問〜折り紙を折ってできる線分、角、面積を求める
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$一辺の長さが2の正方形の折り紙 ABCD を次の手順にしたがって折る。
(1) A と B、DとCを合わせて ADがBCに重なるように谷折りし、折り目をつけて
開く。AB および DC 上にあるこの谷折り線の端点をそれぞれEおよびFとする。
(2 ) AF が谷折り線になるよう に谷折りし、折り目をつけて開く。
(3) A を谷折り線の端点の1つとして、AB がAF 上に重なるように谷折りし、折り
目をつけて開く。BC上にあるこの谷折り線のもう1つの端点をGとする。
(4) D と A、CとBを合わせてDCがABに重なるように谷折りして、折り目をつけ
る。AD およびBC 上にあるこの谷折り線の端点をそれぞれHおよびIとする。
(5) C と B がいずれもGと重なるように2枚重ねて谷折りし、CIおよびBI 上に折り
目をつけて開く。この折り目の点をそれぞれ」およびKとする (A, E, B, K は
それぞれ D, F, C, J と重なっているため図中には表示していない)
(6) HI を谷折り線とする谷折りを開く (A, E, B, KはそれぞれD, F, C, J と重なって
いるため図中には表示していない)
(7) K を谷折り線の端点の1つとして、JがAB上に重なるように谷折りし、折り目
をつける。AD上にあるこの谷折り線のもう1つの端点をしとし、AB上にある
Jが重なる点をMとする。
(8)KLを谷折り戦とする谷折りを開く(MはJと重なっているため表示していない)
(9)Mを谷折り線の端点の1つとして、AとDがそれぞれBEとCF上にくるように
谷折りし、折り目をつけて開く。DC上にあるこの谷折り線のもう1つ端点を
Nとする。
(10)折るのをやめる。
このとき、
$BG=\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }},JK=\boxed{\ \ オカ\ \ }+\sqrt{\boxed{\ \ キク\ \ }},JM=\boxed{\ \ ケコ\ \ },$
$\cos\angle JKM=\frac{\boxed{\ \ サシ\ \ }+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }}$
ここで、$\triangle JKM$の面積を$S_1,\triangle JMN$の面積を$S_2$とすると
$\frac{S_2}{S_1}=\frac{\boxed{\ \ テト\ \ }+\sqrt{\boxed{\ \ ナニ\ \ }}}{\boxed{\ \ ヌネ\ \ }}$
となる。
※(1)~(10)の画像は動画参照
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{4}}$一辺の長さが2の正方形の折り紙 ABCD を次の手順にしたがって折る。
(1) A と B、DとCを合わせて ADがBCに重なるように谷折りし、折り目をつけて
開く。AB および DC 上にあるこの谷折り線の端点をそれぞれEおよびFとする。
(2 ) AF が谷折り線になるよう に谷折りし、折り目をつけて開く。
(3) A を谷折り線の端点の1つとして、AB がAF 上に重なるように谷折りし、折り
目をつけて開く。BC上にあるこの谷折り線のもう1つの端点をGとする。
(4) D と A、CとBを合わせてDCがABに重なるように谷折りして、折り目をつけ
る。AD およびBC 上にあるこの谷折り線の端点をそれぞれHおよびIとする。
(5) C と B がいずれもGと重なるように2枚重ねて谷折りし、CIおよびBI 上に折り
目をつけて開く。この折り目の点をそれぞれ」およびKとする (A, E, B, K は
それぞれ D, F, C, J と重なっているため図中には表示していない)
(6) HI を谷折り線とする谷折りを開く (A, E, B, KはそれぞれD, F, C, J と重なって
いるため図中には表示していない)
(7) K を谷折り線の端点の1つとして、JがAB上に重なるように谷折りし、折り目
をつける。AD上にあるこの谷折り線のもう1つの端点をしとし、AB上にある
Jが重なる点をMとする。
(8)KLを谷折り戦とする谷折りを開く(MはJと重なっているため表示していない)
(9)Mを谷折り線の端点の1つとして、AとDがそれぞれBEとCF上にくるように
谷折りし、折り目をつけて開く。DC上にあるこの谷折り線のもう1つ端点を
Nとする。
(10)折るのをやめる。
このとき、
$BG=\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }},JK=\boxed{\ \ オカ\ \ }+\sqrt{\boxed{\ \ キク\ \ }},JM=\boxed{\ \ ケコ\ \ },$
$\cos\angle JKM=\frac{\boxed{\ \ サシ\ \ }+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }}$
ここで、$\triangle JKM$の面積を$S_1,\triangle JMN$の面積を$S_2$とすると
$\frac{S_2}{S_1}=\frac{\boxed{\ \ テト\ \ }+\sqrt{\boxed{\ \ ナニ\ \ }}}{\boxed{\ \ ヌネ\ \ }}$
となる。
※(1)~(10)の画像は動画参照
2022慶應義塾大学総合政策学部過去問
大学入試問題#246 津田塾大学(2014) #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#津田塾大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x(e^{3x}-1)}{1-\cos\ x}$を求めよ。
出典:2014年津田塾大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x(e^{3x}-1)}{1-\cos\ x}$を求めよ。
出典:2014年津田塾大学 入試問題
福田の数学〜慶應義塾大学2022年総合政策学部第3問〜定積分で表された関数の最小値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}$実数$k \gt 0$ に対して、関数$A(k)=\int_0^2|x^2-kx|dx$とすると
$A(k)=
\left\{\begin{array}{1}
\frac{\boxed{\ \ アイ\ \ }\ k^3+\ \boxed{\ \ ウエ\ \ }\ k^2+\ \boxed{\ \ オカ\ \ }\ k+\ \boxed{\ \ キク\ \ }}{\boxed{\ \ ケコ\ \ }}
(0 \lt k \lt \boxed{\ \ サシ\ \ })
\frac{\boxed{\ \ スセ\ \ }\ k+\ \boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}(\boxed{\ \ サシ\ \ } \leqq k)
\end{array}
\right.$
となる。この関数A(k)が最小となるのは$k=\sqrt{\boxed{\ \ テト\ \ }}$のときで、そのときの
A(k)の値は$\frac{\boxed{\ \ ナニ\ \ }+\boxed{\ \ ヌネ\ \ }\sqrt{\boxed{\ \ ノハ\ \ }}}{\boxed{\ \ ヒフ\ \ }}$
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{3}}$実数$k \gt 0$ に対して、関数$A(k)=\int_0^2|x^2-kx|dx$とすると
$A(k)=
\left\{\begin{array}{1}
\frac{\boxed{\ \ アイ\ \ }\ k^3+\ \boxed{\ \ ウエ\ \ }\ k^2+\ \boxed{\ \ オカ\ \ }\ k+\ \boxed{\ \ キク\ \ }}{\boxed{\ \ ケコ\ \ }}
(0 \lt k \lt \boxed{\ \ サシ\ \ })
\frac{\boxed{\ \ スセ\ \ }\ k+\ \boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}(\boxed{\ \ サシ\ \ } \leqq k)
\end{array}
\right.$
となる。この関数A(k)が最小となるのは$k=\sqrt{\boxed{\ \ テト\ \ }}$のときで、そのときの
A(k)の値は$\frac{\boxed{\ \ ナニ\ \ }+\boxed{\ \ ヌネ\ \ }\sqrt{\boxed{\ \ ノハ\ \ }}}{\boxed{\ \ ヒフ\ \ }}$
2022慶應義塾大学総合政策学部過去問
大学入試問題#245 津田塾大学2014 #三角関数 基本的な問題ですが、数IIの範囲で解ける良問だと思いました。

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#津田塾大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq 2\pi$
$\sin^3\theta+\cos^3\theta$の最大値、最小値を求めよ。
出典:2014年津田塾大学 入試問題
この動画を見る
$0 \leqq \theta \leqq 2\pi$
$\sin^3\theta+\cos^3\theta$の最大値、最小値を求めよ。
出典:2014年津田塾大学 入試問題
大学入試だけど、中学生も解ける!!(東京理科大)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
ある2桁の正の整数mを2乗すると下2桁が36になるとき、
m=?
東京理科大学
この動画を見る
ある2桁の正の整数mを2乗すると下2桁が36になるとき、
m=?
東京理科大学
福田の数学〜慶應義塾大学2022年総合政策学部第2問〜デコボコ数を数える

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$10進法で表したときm桁$(m \gt 0)$である正の整数nの第i桁目$(1 \leqq i \leqq m)$を
$m_i$としたとき、$i\neq j$のとき$n_i\neq n_j$であり、かつ、次の$(\textrm{a})$または$(\textrm{b})$のいずれか
が成り立つとき、nを10進法m桁のデコボコ数と呼ぶことにする。
$(\textrm{a})1 \leqq i \lt m$であるiに対して、
iが奇数の時$n_i \lt n_{i+1}$となり、
iが偶数の時$n_i \gt n_{i+1}$となる。
$(\textrm{b})1 \leqq i \lt m$であるiに対して、$i$が奇数の時$n_i \gt n_{i+1}$となり、
$i$が偶数の時$n_i \lt n_{i+1}$となる。
例えば、361は$(\textrm{a})$を満たす10進法3桁のデコボコ数であり、$52409$は$(\textrm{b})$を
満たす10進法5桁のデコボコ数である。なお、4191は$(\textrm{a})$を満たすが「$i\neq j$のとき
$n_i\neq n_j$である」条件を満たさないため、10進法4桁のデコボコ数ではない。
(1)nが10進法2桁の数$(10 \leqq n \leqq 99)$の場合、
$n_1\neq n_2$であれば$(\textrm{a})$または$(\textrm{b})$を
満たすため、10進法2桁のデコボコ数は$\boxed{\ \ アイ\ \ }$個ある。
(2)nが10進法3桁の数$(100 \leqq n \leqq 999)$の場合、$(\textrm{a})$を満たすデコボコ数は
$\boxed{\ \ ウエオ\ \ }$個、$(\textrm{b})$を満たすデコボコ数は$\boxed{\ \ カキク\ \ }$個あるため、
10進法3桁のデコボコ数は合計$\boxed{\ \ ケコサ\ \ }$個ある。
(3)nが10進法4桁の数$(1000 \leqq n \leqq 9999)$の場合、$(\textrm{a})$を満たすデコボコ数は
$\boxed{\ \ シスセソ\ \ }$個、$(\textrm{b})$を満たすデコボコ数は$\boxed{\ \ タチツテ\ \ }$個あるため、
10進法4桁のデコボコ数は合計$\boxed{\ \ トナニヌ\ \ }$個ある。また10進法4桁のデコボコ数
の中で最も大きなものは$\boxed{\ \ ネノハヒ\ \ }$、最も小さなものは$\boxed{\ \ フヘホマ\ \ }$である。
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{2}}$10進法で表したときm桁$(m \gt 0)$である正の整数nの第i桁目$(1 \leqq i \leqq m)$を
$m_i$としたとき、$i\neq j$のとき$n_i\neq n_j$であり、かつ、次の$(\textrm{a})$または$(\textrm{b})$のいずれか
が成り立つとき、nを10進法m桁のデコボコ数と呼ぶことにする。
$(\textrm{a})1 \leqq i \lt m$であるiに対して、
iが奇数の時$n_i \lt n_{i+1}$となり、
iが偶数の時$n_i \gt n_{i+1}$となる。
$(\textrm{b})1 \leqq i \lt m$であるiに対して、$i$が奇数の時$n_i \gt n_{i+1}$となり、
$i$が偶数の時$n_i \lt n_{i+1}$となる。
例えば、361は$(\textrm{a})$を満たす10進法3桁のデコボコ数であり、$52409$は$(\textrm{b})$を
満たす10進法5桁のデコボコ数である。なお、4191は$(\textrm{a})$を満たすが「$i\neq j$のとき
$n_i\neq n_j$である」条件を満たさないため、10進法4桁のデコボコ数ではない。
(1)nが10進法2桁の数$(10 \leqq n \leqq 99)$の場合、
$n_1\neq n_2$であれば$(\textrm{a})$または$(\textrm{b})$を
満たすため、10進法2桁のデコボコ数は$\boxed{\ \ アイ\ \ }$個ある。
(2)nが10進法3桁の数$(100 \leqq n \leqq 999)$の場合、$(\textrm{a})$を満たすデコボコ数は
$\boxed{\ \ ウエオ\ \ }$個、$(\textrm{b})$を満たすデコボコ数は$\boxed{\ \ カキク\ \ }$個あるため、
10進法3桁のデコボコ数は合計$\boxed{\ \ ケコサ\ \ }$個ある。
(3)nが10進法4桁の数$(1000 \leqq n \leqq 9999)$の場合、$(\textrm{a})$を満たすデコボコ数は
$\boxed{\ \ シスセソ\ \ }$個、$(\textrm{b})$を満たすデコボコ数は$\boxed{\ \ タチツテ\ \ }$個あるため、
10進法4桁のデコボコ数は合計$\boxed{\ \ トナニヌ\ \ }$個ある。また10進法4桁のデコボコ数
の中で最も大きなものは$\boxed{\ \ ネノハヒ\ \ }$、最も小さなものは$\boxed{\ \ フヘホマ\ \ }$である。
2022慶應義塾大学総合政策学部過去問
大学入試問題#244 南山大学(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師:
ますただ
問題文全文(内容文):
$a$:正の定数
$\displaystyle \int_{-a}^{a}\displaystyle \frac{|x|e^x}{(1+e^x)^2}dx$を計算せよ
出典:2014年南山大学 入試問題
この動画を見る
$a$:正の定数
$\displaystyle \int_{-a}^{a}\displaystyle \frac{|x|e^x}{(1+e^x)^2}dx$を計算せよ
出典:2014年南山大学 入試問題
サイコロの確率の問題!注意点があります【数学 入試問題】【九州大学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
4個のサイコロを同時に投げるとき,出る目すべての積を$X$とする。
(1)$X$が25の倍数になる確率を求めよ。
(2)$X$が4の倍数になる確率を求めよ。
(3)$X$が100の倍数になる確率を求めよ。
九州大過去問
この動画を見る
4個のサイコロを同時に投げるとき,出る目すべての積を$X$とする。
(1)$X$が25の倍数になる確率を求めよ。
(2)$X$が4の倍数になる確率を求めよ。
(3)$X$が100の倍数になる確率を求めよ。
九州大過去問
福田の数学〜慶應義塾大学2022年総合政策学部第1問〜ガウス記号を含む数列の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$実数xに対して、x以下の最大の整数を$[x]$と表すことにする。
いま、数列$\left\{a_n\right\}$を
$a_n=[\sqrt{2n}+\frac{1}{2}]$
と定義すると
$a_1=\boxed{\ \ ア\ \ },\ \ \ \ a_2=\boxed{\ \ イ\ \ },\ \ \ \ a_3=\boxed{\ \ ウ\ \ },\ \ \ \ a_4=\boxed{\ \ エ\ \ },\ \ \ \ a_5=\boxed{\ \ オ\ \ },a_6=\boxed{\ \ カ\ \ },$
となる。このとき、$a_n=10$となるのは、$\boxed{\ \ キク\ \ } \leqq n \leqq \boxed{\ \ ケコ\ \ }$の場合に限られる。
また、$\sum_{n=1}^{\boxed{\ \ ケコ\ \ }}a_n=\boxed{\ \ サシスセ\ \ }$である。
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\Large\boxed{1}}$実数xに対して、x以下の最大の整数を$[x]$と表すことにする。
いま、数列$\left\{a_n\right\}$を
$a_n=[\sqrt{2n}+\frac{1}{2}]$
と定義すると
$a_1=\boxed{\ \ ア\ \ },\ \ \ \ a_2=\boxed{\ \ イ\ \ },\ \ \ \ a_3=\boxed{\ \ ウ\ \ },\ \ \ \ a_4=\boxed{\ \ エ\ \ },\ \ \ \ a_5=\boxed{\ \ オ\ \ },a_6=\boxed{\ \ カ\ \ },$
となる。このとき、$a_n=10$となるのは、$\boxed{\ \ キク\ \ } \leqq n \leqq \boxed{\ \ ケコ\ \ }$の場合に限られる。
また、$\sum_{n=1}^{\boxed{\ \ ケコ\ \ }}a_n=\boxed{\ \ サシスセ\ \ }$である。
2022慶應義塾大学総合政策学部過去問
大学入試問題#243 慶應義塾大学(2014) #3次方程式の性質

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$k$:実数
$x^3-kx+1=0$は実数の重解とそれと異なる実数解をもつ
このとき$k$の値を求めよ。
出典:2014年慶應義塾大学 入試問題
この動画を見る
$k$:実数
$x^3-kx+1=0$は実数の重解とそれと異なる実数解をもつ
このとき$k$の値を求めよ。
出典:2014年慶應義塾大学 入試問題
早稲田(商)合同式の基本

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数a,b,c,dは次の条件(i),(ii),(iii)を満たしている.
(i)$3 \leqq a \lt b \lt c \lt d$
(ii)$a-b,b-c$は3の倍数,
(iii)$c^a-b^d$は3の倍数でない$a+b+c+d$の最小値
この動画を見る
整数a,b,c,dは次の条件(i),(ii),(iii)を満たしている.
(i)$3 \leqq a \lt b \lt c \lt d$
(ii)$a-b,b-c$は3の倍数,
(iii)$c^a-b^d$は3の倍数でない$a+b+c+d$の最小値
福田の数学〜慶應義塾大学2022年商学部第4問〜条件付き確率と常用対数の計算

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$ある金属1グラムの価格は正の実数値をとり、ある日の価格は前日に比べ、
確率$\frac{1}{2}$で1.08倍になり(上昇)、確率\frac{1}{2}で0.96倍になる(下落)。この金属の
今日(0日目とする)の価格をAとして、以下の問いに答えなさい。ただし、
必要ならば、$\log_{10}2=0.3010,\ \log_{10}3=0.4771$を用いなさい。
(1)10日目の価格がAよりも高くなるのは、$\boxed{\ \ ア\ \ }$日以上で価格が上昇したとき
である。また、そのような確率は$\frac{\boxed{\ \ イウ\ \ }}{\boxed{\ \ エオ\ \ }}$である。
(2)5日目の価格がAよりも低かった時、10日目の価格がAよりも高い確率
は$\frac{\boxed{\ \ カキ\ \ }}{\boxed{\ \ クケ\ \ }}$である。
(3)10日目の価格がAよりも高かった時、1日目と2日目のうち少なくとも
1回は価格が下落していた確率は$\frac{\boxed{\ \ コサシ\ \ }}{\boxed{\ \ スセソ\ \ }}$である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{4}}$ある金属1グラムの価格は正の実数値をとり、ある日の価格は前日に比べ、
確率$\frac{1}{2}$で1.08倍になり(上昇)、確率\frac{1}{2}で0.96倍になる(下落)。この金属の
今日(0日目とする)の価格をAとして、以下の問いに答えなさい。ただし、
必要ならば、$\log_{10}2=0.3010,\ \log_{10}3=0.4771$を用いなさい。
(1)10日目の価格がAよりも高くなるのは、$\boxed{\ \ ア\ \ }$日以上で価格が上昇したとき
である。また、そのような確率は$\frac{\boxed{\ \ イウ\ \ }}{\boxed{\ \ エオ\ \ }}$である。
(2)5日目の価格がAよりも低かった時、10日目の価格がAよりも高い確率
は$\frac{\boxed{\ \ カキ\ \ }}{\boxed{\ \ クケ\ \ }}$である。
(3)10日目の価格がAよりも高かった時、1日目と2日目のうち少なくとも
1回は価格が下落していた確率は$\frac{\boxed{\ \ コサシ\ \ }}{\boxed{\ \ スセソ\ \ }}$である。
2022慶應義塾大学商学部過去問
大学入試問題#242 神戸大学(2015) 改 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ \sin\ x}{\cos^2x}$dxを計算せよ。
出典:2015年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ \sin\ x}{\cos^2x}$dxを計算せよ。
出典:2015年神戸大学 入試問題
あの公式が力を発揮する良問!微分・積分のよく出る問題です【数学 入試問題】【九州大学】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
この動画を見る
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
式の値 立教大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a-b+c = 1$ , $a^2+b^2+c^2 = 29$のとき
$ac - ab -bc$の値を求めよ
立教大学
この動画を見る
$a-b+c = 1$ , $a^2+b^2+c^2 = 29$のとき
$ac - ab -bc$の値を求めよ
立教大学
福田の数学〜慶應義塾大学2022年商学部第3問〜絶対値の付いた2次関数のグラフと直線の共有点と面積

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$mを実数とし、関数$y=|x^2-5x+4|$のグラフをC、直線$y=mx$を$l$とする。
(1)グラフCと直線lの共有点の個数は
$\boxed{\ \ アイ\ \ } \lt m \lt \boxed{\ \ ウ\ \ }$のとき0個
$m=\boxed{\ \ エオ\ \ }$のとき1個
$m \lt \boxed{\ \ カキ\ \ },\ m=\boxed{\ \ ク\ \ }$,または$m \gt \boxed{\ \ ケ\ \ }$のとき2個
$m=\boxed{\ \ コ\ \ }$のとき3個
$\boxed{\ \ サ\ \ } \lt m \lt \boxed{\ \ シ\ \ }$のとき4個
以下、グラフCと直線lの共有点の個数が3個の場合を考え、
グラフCと直線lの共有点を、x座標が小さい順にP,Q,Rとする。
(2)3点P,Q,Rのx座標は、順に$\boxed{\ \ ス\ \ }-\sqrt{\boxed{\ \ セ\ \ }},\ \boxed{\ \ ソ\ \ },\ \boxed{\ \ タ\ \ }+\sqrt{\boxed{\ \ チ\ \ }}$である。
(3)グラフCと線分QRで囲まれた部分の面積は$\frac{-\ \boxed{\ \ ツ\ \ }+\boxed{\ \ テト\ \ }\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }}$である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{3}}$mを実数とし、関数$y=|x^2-5x+4|$のグラフをC、直線$y=mx$を$l$とする。
(1)グラフCと直線lの共有点の個数は
$\boxed{\ \ アイ\ \ } \lt m \lt \boxed{\ \ ウ\ \ }$のとき0個
$m=\boxed{\ \ エオ\ \ }$のとき1個
$m \lt \boxed{\ \ カキ\ \ },\ m=\boxed{\ \ ク\ \ }$,または$m \gt \boxed{\ \ ケ\ \ }$のとき2個
$m=\boxed{\ \ コ\ \ }$のとき3個
$\boxed{\ \ サ\ \ } \lt m \lt \boxed{\ \ シ\ \ }$のとき4個
以下、グラフCと直線lの共有点の個数が3個の場合を考え、
グラフCと直線lの共有点を、x座標が小さい順にP,Q,Rとする。
(2)3点P,Q,Rのx座標は、順に$\boxed{\ \ ス\ \ }-\sqrt{\boxed{\ \ セ\ \ }},\ \boxed{\ \ ソ\ \ },\ \boxed{\ \ タ\ \ }+\sqrt{\boxed{\ \ チ\ \ }}$である。
(3)グラフCと線分QRで囲まれた部分の面積は$\frac{-\ \boxed{\ \ ツ\ \ }+\boxed{\ \ テト\ \ }\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }}$である。
2022慶應義塾大学商学部過去問
大学入試問題#241 早稲田大学(2014) #指数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
関数$f(x)=(27^x+\displaystyle \frac{1}{27^x})-5(9^x+\displaystyle \frac{1}{9^x})$
$-5(3^x+\displaystyle \frac{1}{3^x})+1$の最小値と、そのときの$x$の値を求めよ。
出典:2014年早稲田大学 入試問題
この動画を見る
関数$f(x)=(27^x+\displaystyle \frac{1}{27^x})-5(9^x+\displaystyle \frac{1}{9^x})$
$-5(3^x+\displaystyle \frac{1}{3^x})+1$の最小値と、そのときの$x$の値を求めよ。
出典:2014年早稲田大学 入試問題
1の三乗根 ω

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1の3乗根のうち虚数であるものの1つをωとすると
$ω^4+ω^3 + 3ω^2 + 2ω +1 =?$
名城大学
この動画を見る
1の3乗根のうち虚数であるものの1つをωとすると
$ω^4+ω^3 + 3ω^2 + 2ω +1 =?$
名城大学
福田の数学〜慶應義塾大学2022年商学部第2問〜空間ベクトルと平面の方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$点Oを原点とするxyz座標空間に、2点A(2,3,1),\ B(-2,1,3)をとる。
また、x座標が正の点Cを、$\overrightarrow{ OC }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$に垂直で、
$|\overrightarrow{ OC }|=8\sqrt3$となるように定める。
(1)$\triangle OAB$の面積は$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$である。
(2)点Cの座標は$(\boxed{\ \ ウ\ \ },\ \boxed{\ \ エオ\ \ },\ \boxed{\ \ カ\ \ })$である。
(3)四面体OABCの体積は$\boxed{\ \ キク\ \ }$である。
(4)平面ABCの方程式は$\ x+\boxed{\ \ ケ\ \ }\ y+\boxed{\ \ コ\ \ }\ z-\ \boxed{\ \ サシ\ \ }=0$である。
(5)原点Oから平面ABCに垂線OHを下ろしたとき、点Hの座標は
$(\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セソ\ \ }},\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }},\frac{\boxed{\ \ ツテ\ \ }}{\boxed{\ \ トナ\ \ }})$
である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{2}}$点Oを原点とするxyz座標空間に、2点A(2,3,1),\ B(-2,1,3)をとる。
また、x座標が正の点Cを、$\overrightarrow{ OC }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$に垂直で、
$|\overrightarrow{ OC }|=8\sqrt3$となるように定める。
(1)$\triangle OAB$の面積は$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$である。
(2)点Cの座標は$(\boxed{\ \ ウ\ \ },\ \boxed{\ \ エオ\ \ },\ \boxed{\ \ カ\ \ })$である。
(3)四面体OABCの体積は$\boxed{\ \ キク\ \ }$である。
(4)平面ABCの方程式は$\ x+\boxed{\ \ ケ\ \ }\ y+\boxed{\ \ コ\ \ }\ z-\ \boxed{\ \ サシ\ \ }=0$である。
(5)原点Oから平面ABCに垂線OHを下ろしたとき、点Hの座標は
$(\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セソ\ \ }},\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }},\frac{\boxed{\ \ ツテ\ \ }}{\boxed{\ \ トナ\ \ }})$
である。
2022慶應義塾大学商学部過去問
大学入試問題#240 防衛医科大学(2020) #曲線の長さ

単元:
#大学入試過去問(数学)#微分とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq t \leqq \pi$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\ t-\cos\ 3t \\
y=3\sin\ t-\sin\ 3t
\end{array}
\right.
\end{eqnarray}$
で表される曲線の長さを求めよ。
出典:2020年防衛医科大学 入試問題
この動画を見る
$0 \leqq t \leqq \pi$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\ t-\cos\ 3t \\
y=3\sin\ t-\sin\ 3t
\end{array}
\right.
\end{eqnarray}$
で表される曲線の長さを求めよ。
出典:2020年防衛医科大学 入試問題
近畿大(理工)整式の剰余

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^{10}-x+1$を$(x-1)^3$で割った余りを求めよ.
近畿大(理工)過去問
この動画を見る
$ x^{10}-x+1$を$(x-1)^3$で割った余りを求めよ.
近畿大(理工)過去問
いつも質問されるので。。。分数式の計算 駒沢大学 数II

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x^2+8x+7}{x^2 -7x+10} \div \frac{x^2-2x-3}{x^2 -5x+6}$
駒澤大学
この動画を見る
$\frac{x^2+8x+7}{x^2 -7x+10} \div \frac{x^2-2x-3}{x^2 -5x+6}$
駒澤大学
福田の数学〜慶應義塾大学2022年商学部第1問(3)〜放物線の法線

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)放物線上の点Pにおける法線とは、点Pを通り点Pにおける接線に
垂直な直線である。放物線$C_1:y=x^2$上の点$P(a,a^2)$(ただし、$a\neq 0$とする)
における法線の方程式は$y=\boxed{\ \ ア\ \ }$である。
また、実数$p,q$に対し、放物線$C_2:y=-(x-p)^2+q$上のある点における
法線が、放物線$C_1$上の点(1,1)における法線と一致するとき、pとqについて
$q=\boxed{\ \ イ\ \ }$という関係式が成り立つ。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(3)放物線上の点Pにおける法線とは、点Pを通り点Pにおける接線に
垂直な直線である。放物線$C_1:y=x^2$上の点$P(a,a^2)$(ただし、$a\neq 0$とする)
における法線の方程式は$y=\boxed{\ \ ア\ \ }$である。
また、実数$p,q$に対し、放物線$C_2:y=-(x-p)^2+q$上のある点における
法線が、放物線$C_1$上の点(1,1)における法線と一致するとき、pとqについて
$q=\boxed{\ \ イ\ \ }$という関係式が成り立つ。
2022慶應義塾大学商学部過去問
大学入試問題#239 弘前大学(2012) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3}(x-\displaystyle \frac{1}{x})(log\ x)^2dx$を計算せよ。
出典:2012年
この動画を見る
$\displaystyle \int_{1}^{3}(x-\displaystyle \frac{1}{x})(log\ x)^2dx$を計算せよ。
出典:2012年
福田の数学〜慶應義塾大学2022年商学部第1問(2)〜三角不等式の一般解

単元:
#大学入試過去問(数学)#三角関数#三角関数とグラフ#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)xを変数とする2次方程式$x^2+(2\sqrt2\cos\theta)x+\sqrt2\sin\theta=0$が
異なる2つの実数解をもつような実数$\theta$の範囲は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(2)xを変数とする2次方程式$x^2+(2\sqrt2\cos\theta)x+\sqrt2\sin\theta=0$が
異なる2つの実数解をもつような実数$\theta$の範囲は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学商学部過去問
福田の数学〜慶應義塾大学2022年商学部第1問(1)〜倍数の個数を数える

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数
は$\boxed{\ \ アイウ\ \ }$個あり、2,3,5の少なくとも1つで割り切れ、
かつ6で割り切れない数は$\boxed{\ \ エオカ\ \ }$個ある。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数
は$\boxed{\ \ アイウ\ \ }$個あり、2,3,5の少なくとも1つで割り切れ、
かつ6で割り切れない数は$\boxed{\ \ エオカ\ \ }$個ある。
2022慶應義塾大学商学部過去問
大学入試問題#237 岡山県立大学(2020) #数学的帰納法

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$(1+2+3+・・・+n)^2=1^3+2^3+3^3+・・・+n^3$が成り立つことを示せ。
$n$:自然数
2020年岡山県立大学 入試問題
この動画を見る
$(1+2+3+・・・+n)^2=1^3+2^3+3^3+・・・+n^3$が成り立つことを示せ。
$n$:自然数
2020年岡山県立大学 入試問題
