学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜北里大学2024医学部第1問(1)〜三角関数の最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
2つの実数x,yは$x^2+y^2 \leqq 4,x \geqq 0 $を満たすとする。このとき、$3x+4y-3$の最小値は$\boxed{ ア }$、最大値は$\boxed{ イ }$である。また、$3x^2+4xy-3y^2$の最大値は$\boxed{ ウ }$である。
この動画を見る
2つの実数x,yは$x^2+y^2 \leqq 4,x \geqq 0 $を満たすとする。このとき、$3x+4y-3$の最小値は$\boxed{ ア }$、最大値は$\boxed{ イ }$である。また、$3x^2+4xy-3y^2$の最大値は$\boxed{ ウ }$である。
福田の数学〜早稲田大学2024社会科学部第3問〜集合と数列
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
この動画を見る
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
福田の数学〜早稲田大学2024商学部第3問〜空間の中の2つの三角形の面積の和の最小値
単元：
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
3 座標空間において、4点をA(0, 0, 2), B(-1, 0, 4), C(1, 1, 0), D(0, 0, 1) とする。次の問いに答えよ。
(1) Pを直線AB上の点とするとき、三角形PCDの面積の最小値を求めよ。
(2) Q,Rを直線 CD上のとし、QR = √3とする。三角形QABの面積と三角形 RAB の面積の和の最小値を求めよ。
この動画を見る
3 座標空間において、4点をA(0, 0, 2), B(-1, 0, 4), C(1, 1, 0), D(0, 0, 1) とする。次の問いに答えよ。
(1) Pを直線AB上の点とするとき、三角形PCDの面積の最小値を求めよ。
(2) Q,Rを直線 CD上のとし、QR = √3とする。三角形QABの面積と三角形 RAB の面積の和の最小値を求めよ。
#電気通信大学2024#極限_72
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{n}{n^2+3k^2}$を解け.
電気通信大学過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{n}{n^2+3k^2}$を解け.
電気通信大学過去問題
福田の数学〜早稲田大学2024商学部第2問〜正24角形の頂点を結んでできる四角形の面積と確率
単元：
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#三角関数#加法定理とその応用#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面において、単位円上の24個の点を${\textrm P}_n(\cos\dfrac{n}{12}\pi,\sin\dfrac{n}{12}\pi)~(n=1,2,3,\cdots,24)$とする。1から24までの番号を付けた24枚のカードから4枚取り出す。取り出したカードの番号を$a,b,c,d$とするとき、点${\textrm P}_a,{\textrm P}_b,{\textrm P}_c,{\textrm P}_d$を頂点とする四角形を$R$とする。四角形$R$の面積の取りうる値を大きい順に$S_1,S_2,S_3$とする。
(1)$S_2$を求めよ。
(2)四角形$R$の面積が$S_3$になる確率を求めよ。
この動画を見る
座標平面において、単位円上の24個の点を${\textrm P}_n(\cos\dfrac{n}{12}\pi,\sin\dfrac{n}{12}\pi)~(n=1,2,3,\cdots,24)$とする。1から24までの番号を付けた24枚のカードから4枚取り出す。取り出したカードの番号を$a,b,c,d$とするとき、点${\textrm P}_a,{\textrm P}_b,{\textrm P}_c,{\textrm P}_d$を頂点とする四角形を$R$とする。四角形$R$の面積の取りうる値を大きい順に$S_1,S_2,S_3$とする。
(1)$S_2$を求めよ。
(2)四角形$R$の面積が$S_3$になる確率を求めよ。
東京大学の整数問題！5つの文字を求める！？どう解く？
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算（整式・展開・因数分解）#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
この動画を見る
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
福田の数学〜早稲田大学2024商学部第1問(4)〜放物線と2本の接線で囲まれた図形の面積
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面において、放物線$y=x^2$を$C$とする。点$P(s,t)$から放物線$C$に異なる2本の接線が引け、その接点をそれぞれ$A,B$とする。線分$PA,PB$と放物線$C$で囲まれた図形の面積が$\displaystyle\frac{144}{125}$であるとき$s,t$の満たす方程式は？
この動画を見る
座標平面において、放物線$y=x^2$を$C$とする。点$P(s,t)$から放物線$C$に異なる2本の接線が引け、その接点をそれぞれ$A,B$とする。線分$PA,PB$と放物線$C$で囲まれた図形の面積が$\displaystyle\frac{144}{125}$であるとき$s,t$の満たす方程式は？
福田の数学〜早稲田大学2024商学部第1問(3)〜漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$C$を$1$でない正の実数とする。正の実数の数列$\{a_n\}$が次の条件を満たしている。
$a_1=C,$${a_n}^{n+1}{a_{n+1}}^n=C^{-(2n+1)}$
このとき、一般項$a_n$を$C$を用いて表せ。
この動画を見る
$C$を$1$でない正の実数とする。正の実数の数列$\{a_n\}$が次の条件を満たしている。
$a_1=C,$${a_n}^{n+1}{a_{n+1}}^n=C^{-(2n+1)}$
このとき、一般項$a_n$を$C$を用いて表せ。
各大学で頻出の典型的な問題！基本的でありながらどの大学でも出題されます【大阪大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
aを実数とする。曲線y=e^x上の各点における法線のうちで、点p(a,3)を通るものの個数をn(a)とする。n(a)を求めよ。
この動画を見る
aを実数とする。曲線y=e^x上の各点における法線のうちで、点p(a,3)を通るものの個数をn(a)とする。n(a)を求めよ。
福田の数学〜早稲田大学2024商学部第1問(2)〜不等式で決定される自然数の列
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$n$を$2$以上の整数とし、$a_1,a_2,a_3,・・・,a_n$を正の整数とする。
$a_1=1,{a_{i+3}}^3\lt 27{a_i}^4(i=1,2,3,・・・,n-1)$
$\displaystyle \sum_{i=1}^{n-1}\frac{a_i}{a_{i+1}}=\frac{a_1}{a_{2}}+\frac{a_2}{a_{3}}+\frac{a_3}{a_{4}}+・・・+\frac{a_{n-1}}{a_{n}}\lt 1$
であるとき、$a_n$のとりうる値の最大値は？
この動画を見る
$n$を$2$以上の整数とし、$a_1,a_2,a_3,・・・,a_n$を正の整数とする。
$a_1=1,{a_{i+3}}^3\lt 27{a_i}^4(i=1,2,3,・・・,n-1)$
$\displaystyle \sum_{i=1}^{n-1}\frac{a_i}{a_{i+1}}=\frac{a_1}{a_{2}}+\frac{a_2}{a_{3}}+\frac{a_3}{a_{4}}+・・・+\frac{a_{n-1}}{a_{n}}\lt 1$
であるとき、$a_n$のとりうる値の最大値は？
福田の数学〜早稲田大学2024教育学部第3問〜法線上の点の座標と最小値
単元：
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
放物線 $C : y = x ^ 2$ 上に点$P(t, t²)$をとる。$C$の点$P$における法線上に点$Q$を、$PQ=1$ であり、点$Q$の$y$座標が点$P$の$y$座標よりも大きくなるようにとる。 点$Q$の$x$座標を$f(t)$ とおく。次の問いに答えよ。
(1) $f(t)$ を求めよ。
(2) $t$が$0\leqq t$の範囲を動くときの$f(t)$の最小値を求めよ。
この動画を見る
放物線 $C : y = x ^ 2$ 上に点$P(t, t²)$をとる。$C$の点$P$における法線上に点$Q$を、$PQ=1$ であり、点$Q$の$y$座標が点$P$の$y$座標よりも大きくなるようにとる。 点$Q$の$x$座標を$f(t)$ とおく。次の問いに答えよ。
(1) $f(t)$ を求めよ。
(2) $t$が$0\leqq t$の範囲を動くときの$f(t)$の最小値を求めよ。
福田の数学〜早稲田大学2024教育学部第2問〜複素数の集合に関する論証
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$3$つの複素数 $z_1, z_2, z_3$に関する条件$P$を次のように定める。
P: 「$z_1, z_2, z_3$はどれも0ではなく、互いに異なり、かつ$ \{{z_1}^n | n は整数\} = \{{z_2}^n | nは整数\} = \{{z_3}^n |n は整数\}$
である。」
次の問いに答えよ。
(1) $3$つの複素数 $z_1,z_2,z_3$が条件$P$を満たしているとする。このとき$ |z_1| = 1$ であることを示せ。また集合$ \{{z_1}^n | n は整数\}$の要素の個数は有限であることを示せ。
(2) 条件$P$を満たす3つの複素数 $z_1,z_2,z_3$のうち、集合$ \{{z_1}^n | n は整数\}$の要素の個数が最小となるものを考える。このとき集合$ \{{z_1}^n | n は整数\}$を求めよ。
この動画を見る
$3$つの複素数 $z_1, z_2, z_3$に関する条件$P$を次のように定める。
P: 「$z_1, z_2, z_3$はどれも0ではなく、互いに異なり、かつ$ \{{z_1}^n | n は整数\} = \{{z_2}^n | nは整数\} = \{{z_3}^n |n は整数\}$
である。」
次の問いに答えよ。
(1) $3$つの複素数 $z_1,z_2,z_3$が条件$P$を満たしているとする。このとき$ |z_1| = 1$ であることを示せ。また集合$ \{{z_1}^n | n は整数\}$の要素の個数は有限であることを示せ。
(2) 条件$P$を満たす3つの複素数 $z_1,z_2,z_3$のうち、集合$ \{{z_1}^n | n は整数\}$の要素の個数が最小となるものを考える。このとき集合$ \{{z_1}^n | n は整数\}$を求めよ。
福田の数学〜早稲田大学2024教育学部第1問(1)〜2進法による循環小数の表記
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\frac{4}{9}$を2進法の循環小数で表せ。
この動画を見る
$\frac{4}{9}$を2進法の循環小数で表せ。
意外と差がつく！互いに素の証明！できるようになっておきたい【一橋大学】【数学 入試問題】
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
nは正の整数とする。n^2と2n+1は互いに素であることを示せ。
この動画を見る
nは正の整数とする。n^2と2n+1は互いに素であることを示せ。
この式はあれしかない！！どう解く？
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
この動画を見る
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
福田の数学〜慶應義塾大学2024環境情報学部第5問〜リーグ戦の確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(1) 6つの大学による野球の総当たり戦を考える。総当たり戦では、どの2つの大学も1試合ずつ対戦し、試合ごとに引き分けなしで勝敗が決定する。いま、 各大学の実力は拮抗していて、勝敗の確率は$\frac{1}{2}$ずつとする。 このとき、全勝する大学が存在する確率は$\frac{\fbox{アイ}}{\fbox{ウエ}}$ 、全勝する大学と全敗する大学が両方存在する確率は$\frac{\fbox{オカキ}}{\fbox{クケコ}}$ 、どの大学も1試合は勝って1試合は負ける確率は$\frac{\fbox{サシス}}{\fbox{セソタ}}$である。
(2) 4つの大学による野球の総当たり戦を考える。総当たり戦では、どの2つの大学も1試合ずつ対戦し、試合ごとに引き分けなしで勝敗が決定する。いま、4つの大学のうちK大学の実力が他の3つの大学よりもまさっていて、K大学が他の大学に勝つ確率は$\frac{3}{4}$負ける確率は$\frac{1}{4}$とする。一方で、K大学以外の3つの大学の2 実力は拮抗していて、これらの大学同士の勝敗の確率は$\frac{1}{2}$ずつとする。このとき、全勝する大学が存在する確率はする確率は、$\frac{\fbox{チツ}}{\fbox{テト}}$、全勝する大学と全敗する大学が両方存在する確率は$\frac{\fbox{ナニ}}{\fbox{ヌネ}}$、どの大学も1試合は勝って1試合は負ける確率は$\frac{\fbox{ノハ}}{\fbox{ヒフ}}$である。
この動画を見る
(1) 6つの大学による野球の総当たり戦を考える。総当たり戦では、どの2つの大学も1試合ずつ対戦し、試合ごとに引き分けなしで勝敗が決定する。いま、 各大学の実力は拮抗していて、勝敗の確率は$\frac{1}{2}$ずつとする。 このとき、全勝する大学が存在する確率は$\frac{\fbox{アイ}}{\fbox{ウエ}}$ 、全勝する大学と全敗する大学が両方存在する確率は$\frac{\fbox{オカキ}}{\fbox{クケコ}}$ 、どの大学も1試合は勝って1試合は負ける確率は$\frac{\fbox{サシス}}{\fbox{セソタ}}$である。
(2) 4つの大学による野球の総当たり戦を考える。総当たり戦では、どの2つの大学も1試合ずつ対戦し、試合ごとに引き分けなしで勝敗が決定する。いま、4つの大学のうちK大学の実力が他の3つの大学よりもまさっていて、K大学が他の大学に勝つ確率は$\frac{3}{4}$負ける確率は$\frac{1}{4}$とする。一方で、K大学以外の3つの大学の2 実力は拮抗していて、これらの大学同士の勝敗の確率は$\frac{1}{2}$ずつとする。このとき、全勝する大学が存在する確率はする確率は、$\frac{\fbox{チツ}}{\fbox{テト}}$、全勝する大学と全敗する大学が両方存在する確率は$\frac{\fbox{ナニ}}{\fbox{ヌネ}}$、どの大学も1試合は勝って1試合は負ける確率は$\frac{\fbox{ノハ}}{\fbox{ヒフ}}$である。
【高校数学】京大の整数問題！どう解く？
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
pを3以上の素数とする。４個の整数a,b,c,dが次の３条件
a+b+c+d=0
ad-bc-+p=0
a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
この動画を見る
pを3以上の素数とする。４個の整数a,b,c,dが次の３条件
a+b+c+d=0
ad-bc-+p=0
a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
#関西大学2024 #方程式_70
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
この動画を見る
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
福田の数学〜慶應義塾大学2024環境情報学部第4問〜球の一部の体積と距離の最大
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
（１）$xyz$空間において、不等式 $x^2+y^2+z^2\leqq |x|$ が定める立体の体積は$\frac{\fbox{アイ}}{\fbox{ウエ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\fbox{オカ}$である。
（２）$xyz$空間において、不等式 $x^2+y^2+z^2\leqq|x|+|y|$ が定める立体の体積は$\frac{\fbox{キク}}{\fbox{ケコ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\sqrt{\fbox{サシ}}$ である。
（３）$xyz$ 空間において、不等式 $x^2+y^2+z^2\leqq$$ |x| + |y| + |z| - \frac{1}{4}$ が定める立体の体積は$(\fbox{スセ}$$+\frac{\fbox{ソタ}}{\fbox{チツ}}\sqrt{\fbox{テト}})\pi$ である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は $\frac{\fbox{ナニ}}{\fbox{ヌネ}}\sqrt{\fbox{ノハ}}$ $+\frac{\fbox{ヒフ}}{\fbox{ヘホ}}\sqrt{\fbox{マミ}}$ である。（ただし、$\fbox{ノハ} \le \fbox{マミ}$ とする。）
この動画を見る
（１）$xyz$空間において、不等式 $x^2+y^2+z^2\leqq |x|$ が定める立体の体積は$\frac{\fbox{アイ}}{\fbox{ウエ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\fbox{オカ}$である。
（２）$xyz$空間において、不等式 $x^2+y^2+z^2\leqq|x|+|y|$ が定める立体の体積は$\frac{\fbox{キク}}{\fbox{ケコ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\sqrt{\fbox{サシ}}$ である。
（３）$xyz$ 空間において、不等式 $x^2+y^2+z^2\leqq$$ |x| + |y| + |z| - \frac{1}{4}$ が定める立体の体積は$(\fbox{スセ}$$+\frac{\fbox{ソタ}}{\fbox{チツ}}\sqrt{\fbox{テト}})\pi$ である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は $\frac{\fbox{ナニ}}{\fbox{ヌネ}}\sqrt{\fbox{ノハ}}$ $+\frac{\fbox{ヒフ}}{\fbox{ヘホ}}\sqrt{\fbox{マミ}}$ である。（ただし、$\fbox{ノハ} \le \fbox{マミ}$ とする。）
福田の数学〜慶應義塾大学2024環境情報学部第3問〜空間ベクトルと四面体の体積
単元：
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
四面体 $\mathrm{ABCD}$ において、$|\overrightarrow{\mathrm{AB}}| = 3,$ $|\overrightarrow{\mathrm{AC}}|$ $=|\overrightarrow{\mathrm{AD}}|$$= |\overrightarrow{\mathrm{BC}}|$$=|\overrightarrow{\mathrm{BD}}|=4,$$|\overrightarrow{\mathrm{CD}}|=5$であるとき $\overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}}$ $=\frac{\fbox{アイ}}{\fbox{ウエ}},$ $\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{AD}}$ $=\frac{\fbox{オカ}}{\fbox{キク}},$ $\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{BD}}$$=\frac{\fbox{ケコ}}{\fbox{サシ}}$
ここで、頂点 $\mathrm{D}$ から $\triangle \mathrm{ABC}$ に下した垂線の足を $\mathrm{H}$ とすると、$\overrightarrow{\mathrm{AH}}$ は $\overrightarrow{\mathrm{AB}}$ と $\overrightarrow{\mathrm{AC}}$ を用いて
$\overrightarrow{\mathrm{AH}}$ $=\frac{\fbox{スセ}}{\fbox{ソタ}} \overrightarrow{\mathrm{AB}}$ $+ \frac{\fbox{チツ}}{\fbox{テト}}\overrightarrow{\mathrm{AC}}$ とあらわすことができる。
垂線 $\mathrm{DH}$ の長さは $\frac{\fbox{ナニ}}{\fbox{ヌネ}}\sqrt{\fbox{ノハ}}$ であるから、四面体 $\mathrm{ABCD}$ の体積は $\frac{\fbox{ヒフ}}{\fbox{ヘホ}}\sqrt{\fbox{マミ}}$ である。
この動画を見る
四面体 $\mathrm{ABCD}$ において、$|\overrightarrow{\mathrm{AB}}| = 3,$ $|\overrightarrow{\mathrm{AC}}|$ $=|\overrightarrow{\mathrm{AD}}|$$= |\overrightarrow{\mathrm{BC}}|$$=|\overrightarrow{\mathrm{BD}}|=4,$$|\overrightarrow{\mathrm{CD}}|=5$であるとき $\overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}}$ $=\frac{\fbox{アイ}}{\fbox{ウエ}},$ $\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{AD}}$ $=\frac{\fbox{オカ}}{\fbox{キク}},$ $\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{BD}}$$=\frac{\fbox{ケコ}}{\fbox{サシ}}$
ここで、頂点 $\mathrm{D}$ から $\triangle \mathrm{ABC}$ に下した垂線の足を $\mathrm{H}$ とすると、$\overrightarrow{\mathrm{AH}}$ は $\overrightarrow{\mathrm{AB}}$ と $\overrightarrow{\mathrm{AC}}$ を用いて
$\overrightarrow{\mathrm{AH}}$ $=\frac{\fbox{スセ}}{\fbox{ソタ}} \overrightarrow{\mathrm{AB}}$ $+ \frac{\fbox{チツ}}{\fbox{テト}}\overrightarrow{\mathrm{AC}}$ とあらわすことができる。
垂線 $\mathrm{DH}$ の長さは $\frac{\fbox{ナニ}}{\fbox{ヌネ}}\sqrt{\fbox{ノハ}}$ であるから、四面体 $\mathrm{ABCD}$ の体積は $\frac{\fbox{ヒフ}}{\fbox{ヘホ}}\sqrt{\fbox{マミ}}$ である。
#関西学院大学2011#方程式_69
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$(x+1)(x-2)(x+3)(x-4)=-24$を解け.
2011関西学院大学過去問題
この動画を見る
$(x+1)(x-2)(x+3)(x-4)=-24$を解け.
2011関西学院大学過去問題
福田の数学〜慶應義塾大学2024環境情報学部第2問〜2べき乗表現の個数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$b_k$を正の整数、$b_{k-1},\cdots,b_1,b_0$を負でない整数とする($k$は負でない整数であり、$k=0$のときは正の整数$b_0$のみを考える)。正の整数$n$に対して、$b_k,b_{k-1},\cdots,b_1,b_0$が$\ \ \ \ $
$\displaystyle 2^kb_k+2^{k-1}b_{k-1}+\cdots+2^2b_2+2b_1+b_0=\sum_{i=0}^k2^ib_i=n\ \\ $を満たすとき、$\langle b_k,b_{k-1},\cdots,b_1,b_0 \rangle$を$n$の2べき乗表現と呼ぶことにする。これは2進法による数の表現と似ているが、2進法の場合とは異なり、$b_i\ (i=0,1,\cdots,k)$は2以上の値も取りうる。そのため$n\geqq 2$において、$n$の2べき乗表現は1通りではない。$\\$
(1)$\ n=3$の2べき乗表現は$\langle 3 \rangle$と$\langle ア, イ\rangle$の2通りである。$\\ $(2)$\ \langle 3,2,1 \rangle$は$n=(ウエ)$の2べき乗表現である。$\\ $(3) $\ m$を正の整数とするとき、1から$m$までの整数を順に並べた$\langle 1,2,\cdots ,m \rangle$は$\ \ 2^{(m+オカ)}+(キク)m+(ケコ)\ $の2べき乗表現である。$\\ $ (4)$\ n$の2べき乗表現の個数を$a_n$とすると、$\ a_4=(サシ),\ a_5=(スセ),\ a_6=(ソタ),\cdots ,a_{10}=(チツ),\cdots , a_{20}=(テト)$である。
この動画を見る
$b_k$を正の整数、$b_{k-1},\cdots,b_1,b_0$を負でない整数とする($k$は負でない整数であり、$k=0$のときは正の整数$b_0$のみを考える)。正の整数$n$に対して、$b_k,b_{k-1},\cdots,b_1,b_0$が$\ \ \ \ $
$\displaystyle 2^kb_k+2^{k-1}b_{k-1}+\cdots+2^2b_2+2b_1+b_0=\sum_{i=0}^k2^ib_i=n\ \\ $を満たすとき、$\langle b_k,b_{k-1},\cdots,b_1,b_0 \rangle$を$n$の2べき乗表現と呼ぶことにする。これは2進法による数の表現と似ているが、2進法の場合とは異なり、$b_i\ (i=0,1,\cdots,k)$は2以上の値も取りうる。そのため$n\geqq 2$において、$n$の2べき乗表現は1通りではない。$\\$
(1)$\ n=3$の2べき乗表現は$\langle 3 \rangle$と$\langle ア, イ\rangle$の2通りである。$\\ $(2)$\ \langle 3,2,1 \rangle$は$n=(ウエ)$の2べき乗表現である。$\\ $(3) $\ m$を正の整数とするとき、1から$m$までの整数を順に並べた$\langle 1,2,\cdots ,m \rangle$は$\ \ 2^{(m+オカ)}+(キク)m+(ケコ)\ $の2べき乗表現である。$\\ $ (4)$\ n$の2べき乗表現の個数を$a_n$とすると、$\ a_4=(サシ),\ a_5=(スセ),\ a_6=(ソタ),\cdots ,a_{10}=(チツ),\cdots , a_{20}=(テト)$である。
差がつく！素数を扱う整数問題！【京都大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
pを３以上の素数とする。４個の整数a,b,c,dが次の３条件
a+b+c+d=0,ad-bc+p=0,a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
この動画を見る
pを３以上の素数とする。４個の整数a,b,c,dが次の３条件
a+b+c+d=0,ad-bc+p=0,a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
福田の数学〜慶應義塾大学2024環境情報学部第1問(2)〜対数不等式
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
\begin{eqnarray}
実数x, y, zが \\
\left\{
\begin{array}{1}
x > 1, \ y > 1 , \ z > 1\\
log_{x}y + log_{y}x + log_{y}z \leqq 6\\
4xz + 3x - 7y - 5z = -5
\end{array}
\right.
\\を満たしているとき \
x = \frac{\fbox{アイ}}{\fbox{ウエ}}, \
y = \frac{\fbox{オカ}}{\fbox{キク}}, \
z = \frac{\fbox{ケコ}}{\fbox{サシ}},
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
実数x, y, zが \\
\left\{
\begin{array}{1}
x > 1, \ y > 1 , \ z > 1\\
log_{x}y + log_{y}x + log_{y}z \leqq 6\\
4xz + 3x - 7y - 5z = -5
\end{array}
\right.
\\を満たしているとき \
x = \frac{\fbox{アイ}}{\fbox{ウエ}}, \
y = \frac{\fbox{オカ}}{\fbox{キク}}, \
z = \frac{\fbox{ケコ}}{\fbox{サシ}},
\end{eqnarray}
$
#関西学院大学2006#不定積分_68
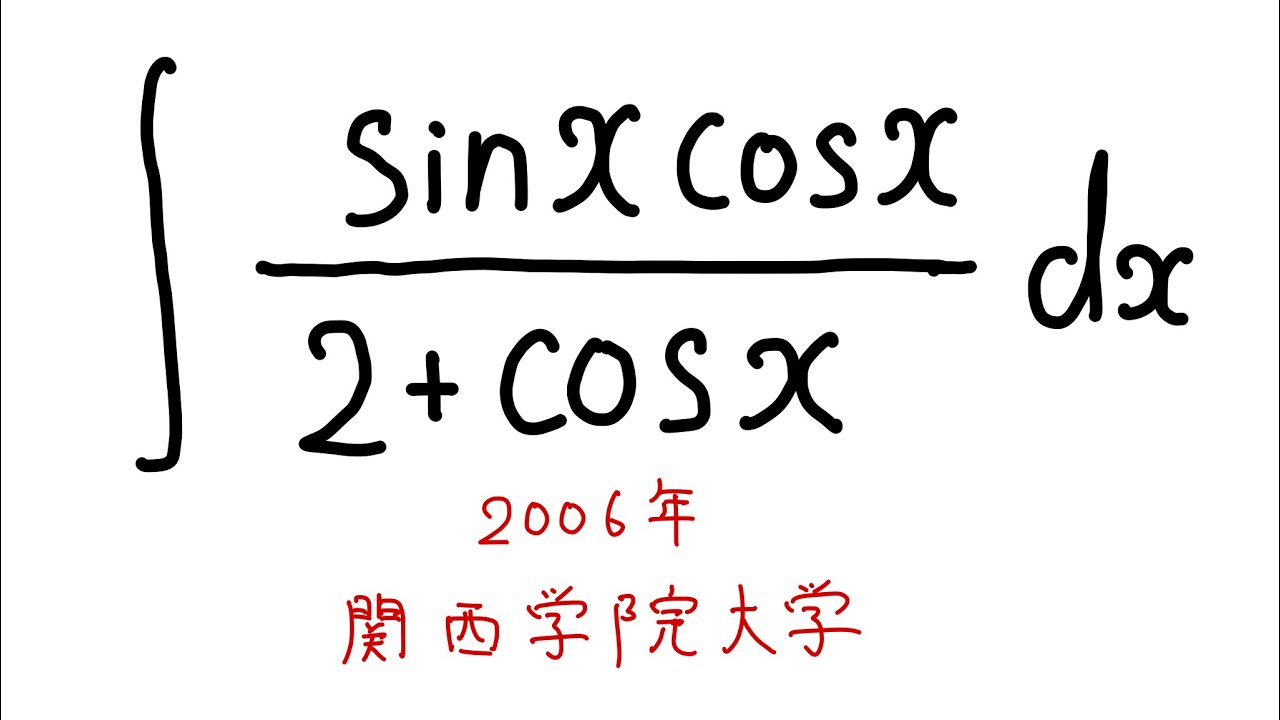
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \dfrac{\sin x \cos x}{2+\cos \ x} dx$を解け.
2006関西学院大学過去問
この動画を見る
$\displaystyle \int \dfrac{\sin x \cos x}{2+\cos \ x} dx$を解け.
2006関西学院大学過去問
福田の数学〜慶應義塾大学2024環境情報学部第1問(1)〜相加平均と相乗平均の関係
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x,y$ を正の実数とするとき、$\displaystyle 27x + \frac{3x}{y} + \frac{2y}{x}$ は $\displaystyle x=\frac{\fbox{アイ}}{\fbox{ウエ}},$ $\displaystyle y= \frac{\fbox{オカ}}{\fbox{キク}}$ において最小値 $\fbox{ケコ}$ をとる。
この動画を見る
$x,y$ を正の実数とするとき、$\displaystyle 27x + \frac{3x}{y} + \frac{2y}{x}$ は $\displaystyle x=\frac{\fbox{アイ}}{\fbox{ウエ}},$ $\displaystyle y= \frac{\fbox{オカ}}{\fbox{キク}}$ において最小値 $\fbox{ケコ}$ をとる。
#関西学院大学2019#不定積分_67
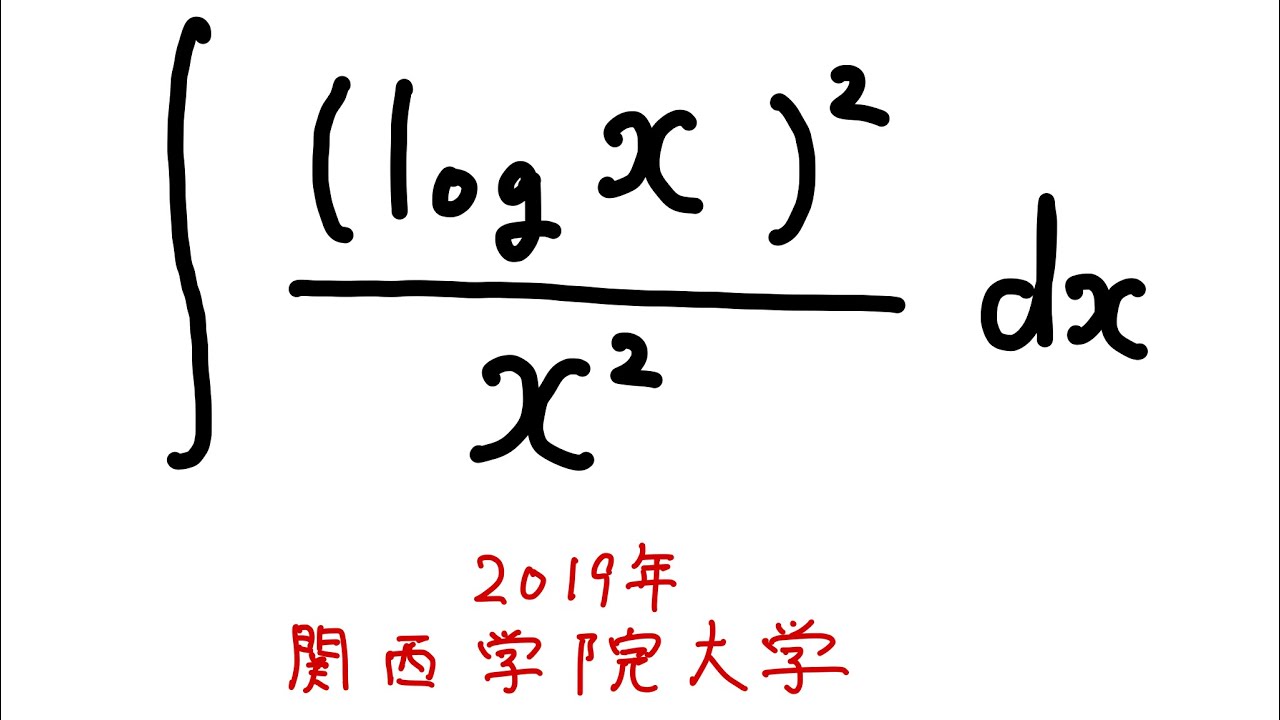
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \dfrac{(\log x)^2}{x^2} dx$を解け.
2019関西学院大学過去問
この動画を見る
$\displaystyle \int \dfrac{(\log x)^2}{x^2} dx$を解け.
2019関西学院大学過去問
#関西学院大学2006#不定積分_66
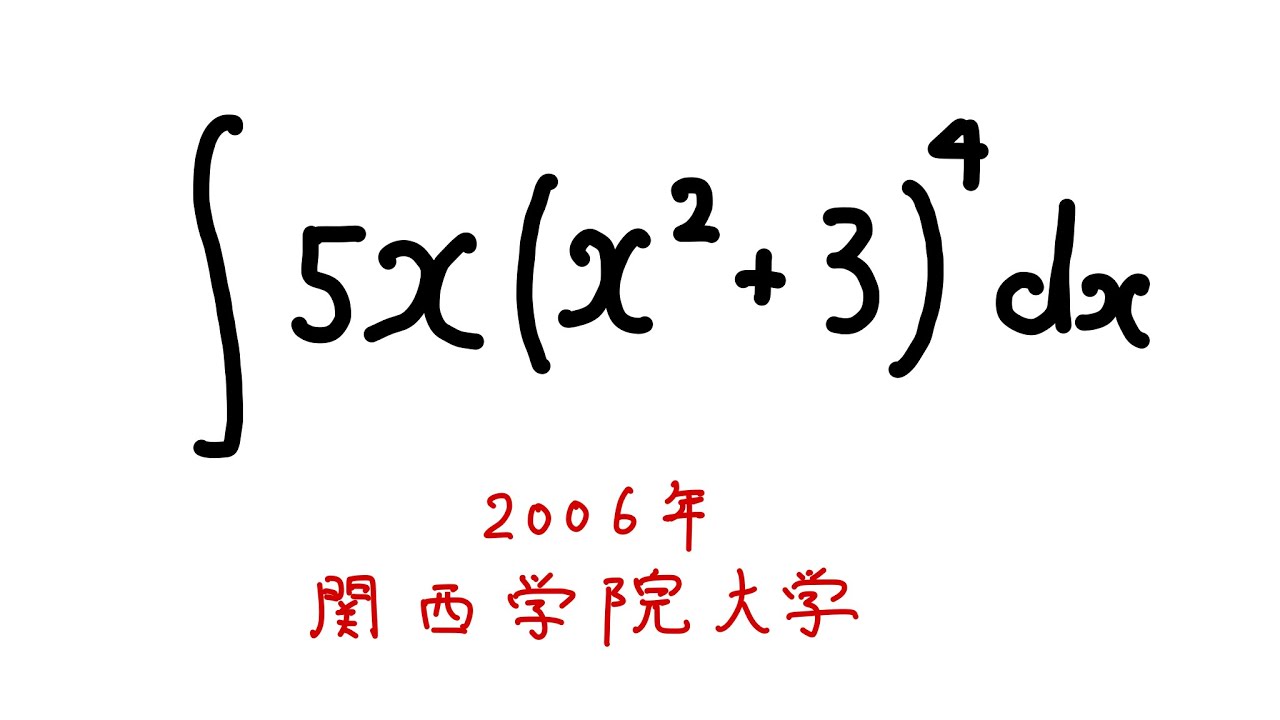
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$ \int 5x(x^2+3)^4 \ dx$を解け.
2006関西学院大学過去問
この動画を見る
$ \int 5x(x^2+3)^4 \ dx$を解け.
2006関西学院大学過去問
福田の数学〜慶應義塾大学2024総合政策学部第4問〜中がくり抜かれた球の体積
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$点Oを中心とする半径$2$の球から点を中心とする半径$r(0 \lt r\lt 2)$の球をくり抜いてできた立体$V$がある。いま、点Oからおろした垂線の長さが$x(0 \lt x\lt 2)$である平面$P$で立体$V$を切り、2つの立体に分ける。2つの立体のうち、体積の小さい方を$V_{ 1 }$、大きい方を$V_{2}$とする。
(1)平面$P$による立体$V$の切り口の面積が$π(2-r)^2$であるとき、$x=\sqrt{ \boxed{ アイ }r^2+\boxed{ ウエ } }$である。
(2)$(0 \lt x\lt r)$のとき、$V_{1}$の体積は$(r^2+\boxed{ オカ})πx+\frac{\boxed{キク}}{\boxed{ケコ}}πr^3+\frac{\boxed{サシ}}{\boxed{スセ}}π$であり、$r \leqq x\lt2$のとき、$V_{1}$の体積は$\frac{\boxed{ソタ}}{\boxed{チツ}}πr^3+\boxed{テト}πx+\frac{\boxed{ナニ}}{\boxed{ヌネ}}π$である。
(3)$x=r$において、$V_{1}$の体積と$V_{2}$の体積の比が$1:3$になるとき、$r=\boxed{ノハ}+\sqrt{\boxed{ヒフ}}$である。また、$x=\frac{2}{3}r$において$V_{1}$の体積と$V_{2}$の体積の比が$1:3$になるとき、$r=\boxed{ヘホ}+\sqrt{\boxed{マミ}}$である。
この動画を見る
$\boxed{4}$点Oを中心とする半径$2$の球から点を中心とする半径$r(0 \lt r\lt 2)$の球をくり抜いてできた立体$V$がある。いま、点Oからおろした垂線の長さが$x(0 \lt x\lt 2)$である平面$P$で立体$V$を切り、2つの立体に分ける。2つの立体のうち、体積の小さい方を$V_{ 1 }$、大きい方を$V_{2}$とする。
(1)平面$P$による立体$V$の切り口の面積が$π(2-r)^2$であるとき、$x=\sqrt{ \boxed{ アイ }r^2+\boxed{ ウエ } }$である。
(2)$(0 \lt x\lt r)$のとき、$V_{1}$の体積は$(r^2+\boxed{ オカ})πx+\frac{\boxed{キク}}{\boxed{ケコ}}πr^3+\frac{\boxed{サシ}}{\boxed{スセ}}π$であり、$r \leqq x\lt2$のとき、$V_{1}$の体積は$\frac{\boxed{ソタ}}{\boxed{チツ}}πr^3+\boxed{テト}πx+\frac{\boxed{ナニ}}{\boxed{ヌネ}}π$である。
(3)$x=r$において、$V_{1}$の体積と$V_{2}$の体積の比が$1:3$になるとき、$r=\boxed{ノハ}+\sqrt{\boxed{ヒフ}}$である。また、$x=\frac{2}{3}r$において$V_{1}$の体積と$V_{2}$の体積の比が$1:3$になるとき、$r=\boxed{ヘホ}+\sqrt{\boxed{マミ}}$である。
#慶應義塾大学2024#対数_65#Shorts
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$ x\gt 1,y \gt 1,z \gt 1$
$\log_x y +\log_y x+\log_y z+4\log_z y \leqq 6$
$4xz+3x-7y-5z=-5$
を満たす$x,y,z$の値を求めよ.
2024慶應義塾大学環境情報学部過去問題
この動画を見る
$ x\gt 1,y \gt 1,z \gt 1$
$\log_x y +\log_y x+\log_y z+4\log_z y \leqq 6$
$4xz+3x-7y-5z=-5$
を満たす$x,y,z$の値を求めよ.
2024慶應義塾大学環境情報学部過去問題