 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
大学入試問題#160 名古屋市立大学(2020) 三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq \pi$
$\cos4\theta=\cos2\theta$をみたす$\theta$をすべて求めよ。
出典:2020年名古屋市立大学 入試問題
この動画を見る
$0 \leqq \theta \leqq \pi$
$\cos4\theta=\cos2\theta$をみたす$\theta$をすべて求めよ。
出典:2020年名古屋市立大学 入試問題
福田の数学〜東京工業大学2022年理系第5問〜定積分と不等式と区分求積

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aは$0 \lt a \leqq \frac{\pi}{4}$を満たす実数とし、
$f(x)=\frac{4}{3}\sin(\frac{\pi}{4}+ax)\cos(\frac{\pi}{4}-ax)$
とする。このとき、次の問いに答えよ。
(1)次の等式(*)を満たすaがただ1つ存在することを示せ。
(*) $\int_0^1f(x)dx=1$
(2)$0 \leqq b \lt c \leqq 1$を満たす実数b,cについて、不等式
$f(b)(c-b) \leqq \int_b^cf(x)dx \leqq f(c)(c-b)$
が成り立つことを示せ。
(3)次の試行を考える。\\
[試行]n個の数$1,2,\ldots\ldots,n$を出目とする、あるルーレットをk回まわす。
この試行において、各$i=1,2,\ldots\ldots,n$についてiが出た回数を$S_{n,k,i}$とし、
(**)$\lim_{k \to \infty}\frac{S_{n,k,i}}{k}=\int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx$
が成り立つとする。このとき、(1)の等式(*)が成り立つことを示せ。
(4)(3)の[試行]において出た数の平均値を$A_{n,k}$とし、$A_n=\lim_{k \to \infty}A_{n,k}$とする。
(**)が成り立つとき、極限$\lim_{n \to \infty}\frac{A_n}{n}$をaを用いて表せ。
2022東京工業大学理系過去問
この動画を見る
aは$0 \lt a \leqq \frac{\pi}{4}$を満たす実数とし、
$f(x)=\frac{4}{3}\sin(\frac{\pi}{4}+ax)\cos(\frac{\pi}{4}-ax)$
とする。このとき、次の問いに答えよ。
(1)次の等式(*)を満たすaがただ1つ存在することを示せ。
(*) $\int_0^1f(x)dx=1$
(2)$0 \leqq b \lt c \leqq 1$を満たす実数b,cについて、不等式
$f(b)(c-b) \leqq \int_b^cf(x)dx \leqq f(c)(c-b)$
が成り立つことを示せ。
(3)次の試行を考える。\\
[試行]n個の数$1,2,\ldots\ldots,n$を出目とする、あるルーレットをk回まわす。
この試行において、各$i=1,2,\ldots\ldots,n$についてiが出た回数を$S_{n,k,i}$とし、
(**)$\lim_{k \to \infty}\frac{S_{n,k,i}}{k}=\int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx$
が成り立つとする。このとき、(1)の等式(*)が成り立つことを示せ。
(4)(3)の[試行]において出た数の平均値を$A_{n,k}$とし、$A_n=\lim_{k \to \infty}A_{n,k}$とする。
(**)が成り立つとき、極限$\lim_{n \to \infty}\frac{A_n}{n}$をaを用いて表せ。
2022東京工業大学理系過去問
大学入試問題#159 横浜国立大学 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{4}\displaystyle \frac{dx}{\sqrt{ 3-\sqrt{ x } }}$を計算せよ
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{4}\displaystyle \frac{dx}{\sqrt{ 3-\sqrt{ x } }}$を計算せよ
出典:横浜国立大学 入試問題
福田の入試問題解説〜北海道大学2022年文系第4問〜復元抽出と非復元抽出の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
箱の中に1文字ずつ書かれたカードが10枚ある。そのうち5枚にはA、
3枚にはB、2枚にはCと書かれている。箱から1枚ずつ、3回カードを
取り出す試行を考える。
(1)カードを取り出すごとに箱に戻す場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(2)取り出したカードを箱に戻さない場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(3)取り出したカードを箱に戻さない場合、2回目に取り出したカードの文字が
Cであるとき、1回目と3回目に取り出したカードの文字が一致する
条件つき確率を求めよ。
2022北海道大学文系過去問
この動画を見る
箱の中に1文字ずつ書かれたカードが10枚ある。そのうち5枚にはA、
3枚にはB、2枚にはCと書かれている。箱から1枚ずつ、3回カードを
取り出す試行を考える。
(1)カードを取り出すごとに箱に戻す場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(2)取り出したカードを箱に戻さない場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(3)取り出したカードを箱に戻さない場合、2回目に取り出したカードの文字が
Cであるとき、1回目と3回目に取り出したカードの文字が一致する
条件つき確率を求めよ。
2022北海道大学文系過去問
福田の数学〜東京工業大学2022年理系第4問〜複素数平面上の点の軌跡と線分の通過範囲

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
aを正の実数とする。複素数$z$が$|z-1|=a$かつ$z\neq \frac{1}{2}$を満たしながら
動くとき、複素数平面上の点$w=\frac{z-3}{1-2z}$が描く図形をKとする。
このとき、次の問いに答えよ。
(1)Kが円となるためのaの条件を求めよ。また、そのとき
Kの中心が表す複素数とKの半径を、それぞれaを用いて表せ。
(2)aが(1)の条件を満たしながら動くとき、虚軸に平行で円Kの直径となる
線分が通過する領域を複素数平面上に図示せよ。
2022東京工業大学理系過去問
この動画を見る
aを正の実数とする。複素数$z$が$|z-1|=a$かつ$z\neq \frac{1}{2}$を満たしながら
動くとき、複素数平面上の点$w=\frac{z-3}{1-2z}$が描く図形をKとする。
このとき、次の問いに答えよ。
(1)Kが円となるためのaの条件を求めよ。また、そのとき
Kの中心が表す複素数とKの半径を、それぞれaを用いて表せ。
(2)aが(1)の条件を満たしながら動くとき、虚軸に平行で円Kの直径となる
線分が通過する領域を複素数平面上に図示せよ。
2022東京工業大学理系過去問
大学入試問題#158 名古屋市立大学(2020) 2項展開の応用

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
ますただ
問題文全文(内容文):
$(x+2y)^2(x+2y+3z)^4$を展開した時
$x^4y^2,x^3y^2z$の係数をそれぞれ求めよ。
出典:2020年名古屋市立大学 入試問題
この動画を見る
$(x+2y)^2(x+2y+3z)^4$を展開した時
$x^4y^2,x^3y^2z$の係数をそれぞれ求めよ。
出典:2020年名古屋市立大学 入試問題
福田の入試問題解説〜北海道大学2022年文系第3問〜直角三角形と内接円

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
この動画を見る
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
大学入試問題#157 旭川医科大学(2014) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}log(1+x^2)dx$を求めよ。
出典:2014年旭川医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}log(1+x^2)dx$を求めよ。
出典:2014年旭川医科大学 入試問題
福田の数学〜東京工業大学2022年理系第3問〜直角三角形の頂点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\alphaは0 \lt \alpha \lt \frac{\pi}{2}$を満たす実数とする。
$\angle A=\alpha$および$\angle P=\frac{\pi}{2}$を満たす直角三角形APB
が、次の2つの条件$(\textrm{a}),(\textrm{b})$を満たしながら、時刻t=0から時刻$t=\frac{\pi}{2}$まで
xy平面上を動くとする。
$(\textrm{a})$時刻tでの点A,Bの座標は、それぞれ$A(\sin t,0),B(0, \cos t)$である。
$(\textrm{b})$点Pは第一象限内にある。
このとき、次の問いに答えよ。
(1)点Pはある直線上を動くことを示し、その直線の方程式を$\alpha$を用いて表せ。
(2)時刻$t=0$から時刻$t=\frac{\pi}{2}$までの間に点Pが動く道のりを$\alpha$を用いて表せ。
(3)xy平面内において、連立不等式
$x^2-x+y^2 \lt 0, x^2+y^2-y \lt 0$
により定まる領域をDとする。このとき、点Pは領域Dには入らないことを示せ。
2022東京工業大学理系過去問
この動画を見る
$\alphaは0 \lt \alpha \lt \frac{\pi}{2}$を満たす実数とする。
$\angle A=\alpha$および$\angle P=\frac{\pi}{2}$を満たす直角三角形APB
が、次の2つの条件$(\textrm{a}),(\textrm{b})$を満たしながら、時刻t=0から時刻$t=\frac{\pi}{2}$まで
xy平面上を動くとする。
$(\textrm{a})$時刻tでの点A,Bの座標は、それぞれ$A(\sin t,0),B(0, \cos t)$である。
$(\textrm{b})$点Pは第一象限内にある。
このとき、次の問いに答えよ。
(1)点Pはある直線上を動くことを示し、その直線の方程式を$\alpha$を用いて表せ。
(2)時刻$t=0$から時刻$t=\frac{\pi}{2}$までの間に点Pが動く道のりを$\alpha$を用いて表せ。
(3)xy平面内において、連立不等式
$x^2-x+y^2 \lt 0, x^2+y^2-y \lt 0$
により定まる領域をDとする。このとき、点Pは領域Dには入らないことを示せ。
2022東京工業大学理系過去問
福田の入試問題解説〜北海道大学2022年文系第2問〜数列の一般項の最小と部分和の最小

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\left\{a_n\right\}$を$a_1=-15$および
$a_{n+1}=a_n+\frac{n}{5}-2 (n=1,2,3,\ldots)$
を満たす数列とする。
(1)$a_n$が最小となる自然数nを全て求めよ。
(2)$\left\{a_n\right\}$の一般項を求めよ。
(3)$\sum_{k=1}^na_k$が最小となる自然数nを全て求めよ。
2022北海道大学文系過去問
この動画を見る
$\left\{a_n\right\}$を$a_1=-15$および
$a_{n+1}=a_n+\frac{n}{5}-2 (n=1,2,3,\ldots)$
を満たす数列とする。
(1)$a_n$が最小となる自然数nを全て求めよ。
(2)$\left\{a_n\right\}$の一般項を求めよ。
(3)$\sum_{k=1}^na_k$が最小となる自然数nを全て求めよ。
2022北海道大学文系過去問
大学入試問題#156 昭和大学(2019) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#昭和大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2}\displaystyle \frac{dx}{x^2-2x+2}$を求めよ。
出典:2019年昭和大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2}\displaystyle \frac{dx}{x^2-2x+2}$を求めよ。
出典:2019年昭和大学 入試問題
福田の数学〜東工大2022理系1修正版

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
この動画を見る
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
福田の数学〜東京工業大学2022年理系第2問〜3つの数の最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
3つの正の整数a,b,cの最大公約数が1であるとき、次の問いに答えよ。
(1)$a+b+c,ab+bc+ca,abc$の最大公約数は1であることを示せ。
(2)$a+b+c,a^2+b^2+c^2,a^3+b^3+c^3$の最大公約数となるような正の整数を
全て求めよ。
2022東京工業大学理系過去問
この動画を見る
3つの正の整数a,b,cの最大公約数が1であるとき、次の問いに答えよ。
(1)$a+b+c,ab+bc+ca,abc$の最大公約数は1であることを示せ。
(2)$a+b+c,a^2+b^2+c^2,a^3+b^3+c^3$の最大公約数となるような正の整数を
全て求めよ。
2022東京工業大学理系過去問
大学入試問題#155 琉球大学(1987) 極限
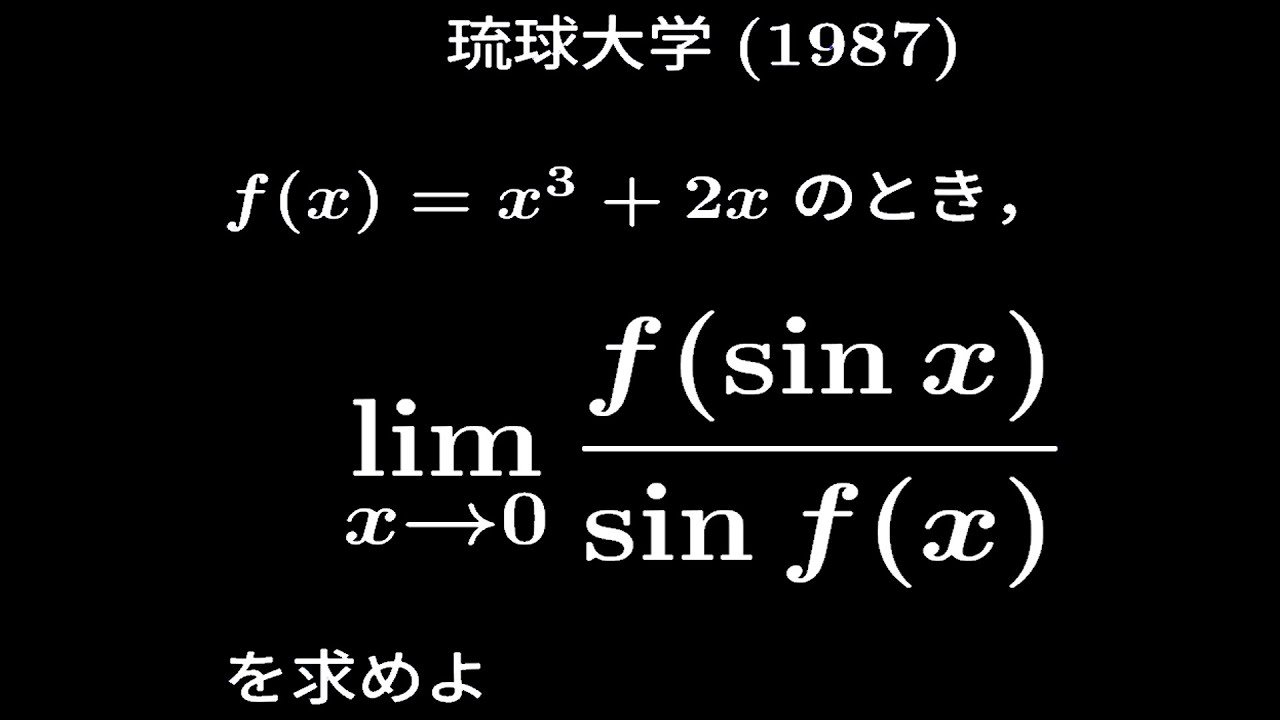
単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x^3+2x$のとき
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(\sin\ x)}{\sin\ f(x)}$を求めよ。
出典:1987年琉球大学 入試問題
この動画を見る
$f(x)=x^3+2x$のとき
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(\sin\ x)}{\sin\ f(x)}$を求めよ。
出典:1987年琉球大学 入試問題
大学入試問題#154 横浜市立大学医学部(2017) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{\cos\ 2x}\ dx$を求めよ。
出典:2017年横浜市立大学医学部 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{\cos\ 2x}\ dx$を求めよ。
出典:2017年横浜市立大学医学部 入試問題
福田の入試問題解説〜北海道大学2022年文系第1問〜剰余定理と高次不等式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
kを実数の定数とし、
$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-k+1$
とする。
(1)$f(k-1)$の値を求めよ。
(2)$|k|\lt 2$のとき、不等式$f(x) \geqq 0$を解け。
2022北海道大学文系過去問
この動画を見る
kを実数の定数とし、
$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-k+1$
とする。
(1)$f(k-1)$の値を求めよ。
(2)$|k|\lt 2$のとき、不等式$f(x) \geqq 0$を解け。
2022北海道大学文系過去問
福田の数学〜東京工業大学2022年理系第1問〜2次方程式の解の存在範囲

単元:
#大学入試過去問(数学)#2次関数#複素数平面#2次方程式と2次不等式#図形への応用#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
この動画を見る
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
大学入試問題#153 東京医科大学(2017) 微積の応用

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学#東京医科大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{x}\displaystyle \frac{x+4t}{\sqrt{ 3x^4+t^4 }}\ dt$において$f'(x)$を求めよ。
出典:2017年東京医科大学 入試問題
この動画を見る
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{x}\displaystyle \frac{x+4t}{\sqrt{ 3x^4+t^4 }}\ dt$において$f'(x)$を求めよ。
出典:2017年東京医科大学 入試問題
福田の数学〜京都大学2022年文系第4問〜線分の中点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを正の実数とする。直線$L:ax+by=1$と曲線$y=-\frac{1}{x}$との2つの交点
のうち、y座標が正のものをP、負のものをQとする。また、Lとx軸との交点を
Rとし、Lとy軸との交点をSとする。a,bが条件
$\frac{PQ}{RS}=\sqrt2$
を満たしながら動くとき、線分PQの中点の軌跡を求めよ。
2022京都大学文系過去問
この動画を見る
a,bを正の実数とする。直線$L:ax+by=1$と曲線$y=-\frac{1}{x}$との2つの交点
のうち、y座標が正のものをP、負のものをQとする。また、Lとx軸との交点を
Rとし、Lとy軸との交点をSとする。a,bが条件
$\frac{PQ}{RS}=\sqrt2$
を満たしながら動くとき、線分PQの中点の軌跡を求めよ。
2022京都大学文系過去問
大学入試問題#152 東京工業大学(2002) 極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{log\ n}(1+\displaystyle \frac{1}{2}+・・・+\displaystyle \frac{1}{n})$を求めよ。
出典:2002年東京工業大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{log\ n}(1+\displaystyle \frac{1}{2}+・・・+\displaystyle \frac{1}{n})$を求めよ。
出典:2002年東京工業大学 入試問題
福田の数学・入試問題解説〜東北大学2022年理系第6問〜円柱と球の共通部分の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
この動画を見る
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
大学入試問題#151 東北大学2020 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(1+x^2)^3}$を計算せよ。
出典:2020年東北大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(1+x^2)^3}$を計算せよ。
出典:2020年東北大学 入試問題
2022九州大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
kは実数であり,整式f(x)を$ f(x)=x^4+6x^3-kx^2+2kx-64 $で定める.
f(x)=0が虚数解をもつとき,
(1)f(x)はx-2で割り切れることを示せ.
(2)f(x)=0は負の実数解をもつことを示せ.
(3)f(x)=0のすべての実数解が整数で,すべての虚数解の実部と虚部が
ともに整数である.kの値を求めよ.
2022九州大過去問
この動画を見る
kは実数であり,整式f(x)を$ f(x)=x^4+6x^3-kx^2+2kx-64 $で定める.
f(x)=0が虚数解をもつとき,
(1)f(x)はx-2で割り切れることを示せ.
(2)f(x)=0は負の実数解をもつことを示せ.
(3)f(x)=0のすべての実数解が整数で,すべての虚数解の実部と虚部が
ともに整数である.kの値を求めよ.
2022九州大過去問
福田の数学〜京都大学2022年文系第3問〜放物線と直交する2接線で囲まれる面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
xy平面上の2直線$L_1,L_2$は直交し、交点のx座標は$\frac{3}{2}$である。
また、$L_1,L_2$は共に曲線$C:y=\frac{x^2}{4}$に接している。このとき、$L_1,L_2$およびCで
囲まれる図形の面積を求めよ。
2022京都大学文系過去問
この動画を見る
xy平面上の2直線$L_1,L_2$は直交し、交点のx座標は$\frac{3}{2}$である。
また、$L_1,L_2$は共に曲線$C:y=\frac{x^2}{4}$に接している。このとき、$L_1,L_2$およびCで
囲まれる図形の面積を求めよ。
2022京都大学文系過去問
大学入試問題#150 京都大学(1991) 積分の応用

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$a$実数
$e^x \geqq e^a+(x-1)e^a$を示せ
(2)
$\displaystyle \int_{0}^{1}e^{\sin\ \pi\ x}dx \geqq e^{\frac{2}{x}}$を示せ
出典:1991年京都大学 入試問題
この動画を見る
(1)
$a$実数
$e^x \geqq e^a+(x-1)e^a$を示せ
(2)
$\displaystyle \int_{0}^{1}e^{\sin\ \pi\ x}dx \geqq e^{\frac{2}{x}}$を示せ
出典:1991年京都大学 入試問題
2022九州大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数m,nは$ n^4=1+210m^2 $を満たす.
(1)$\dfrac{n^2+1}{2},\dfrac{n^2-1}{2}$は互いに素な整数であることを示せ.
(2)$ n^2-1 $は168の倍数であることを示せ.
(3)(m,n)を1組求めよ.
2022九州大過去問
この動画を見る
自然数m,nは$ n^4=1+210m^2 $を満たす.
(1)$\dfrac{n^2+1}{2},\dfrac{n^2-1}{2}$は互いに素な整数であることを示せ.
(2)$ n^2-1 $は168の倍数であることを示せ.
(3)(m,n)を1組求めよ.
2022九州大過去問
福田の数学・入試問題解説〜東北大学2022年理系第5問〜空間内の直線上の点列の極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間内において、ベクトル
$\overrightarrow{ a }=(1,2,1), \overrightarrow{ b }=(1,1,-1), \overrightarrow{ c }=(0,0,1)$
が定める直線
$l:s\overrightarrow{ a }, l':t\overrightarrow{ b }+\overrightarrow{ c }$
を考える。点$A_1$を原点(0,0,0)とし、点$A_1$から直線l'に下ろした垂線$A_1B_1$と
おく。次に、点$B_1(t_1\overrightarrow{ b }+\overrightarrow{ c })$から直線lに下ろした垂線を$B_1A_2$とおく。
同様に、点$A_k(s_k\overrightarrow{ a })$から直線l'に下ろした垂線を$A_kB_k$、点$B_k(t_k\overrightarrow{ b }+\overrightarrow{ c })$から直線l
に下ろした垂線を$B_kA_{k+1}$とする手順を繰り返して、点$A_n(s_n\overrightarrow{ a }),B_n(t_n\overrightarrow{ b }+\overrightarrow{ c })$
(nは正の整数)を定める。
(1)$s_n$を用いて$s_{n+1}$を表せ。
(2)極限値$S=\lim_{n \to \infty}s_n, T=\lim_{n \to \infty}t_n$を求めよ。
(3)(2)で求めたS,Tに対して、点A,Bをそれぞれ$A(S\overrightarrow{ a }),B(T\overrightarrow{ b }+\overrightarrow{ c })$とおくと、
直線ABは2直線l,l'の両方と直交することを示せ。
2022東北大学理系過去問
この動画を見る
座標空間内において、ベクトル
$\overrightarrow{ a }=(1,2,1), \overrightarrow{ b }=(1,1,-1), \overrightarrow{ c }=(0,0,1)$
が定める直線
$l:s\overrightarrow{ a }, l':t\overrightarrow{ b }+\overrightarrow{ c }$
を考える。点$A_1$を原点(0,0,0)とし、点$A_1$から直線l'に下ろした垂線$A_1B_1$と
おく。次に、点$B_1(t_1\overrightarrow{ b }+\overrightarrow{ c })$から直線lに下ろした垂線を$B_1A_2$とおく。
同様に、点$A_k(s_k\overrightarrow{ a })$から直線l'に下ろした垂線を$A_kB_k$、点$B_k(t_k\overrightarrow{ b }+\overrightarrow{ c })$から直線l
に下ろした垂線を$B_kA_{k+1}$とする手順を繰り返して、点$A_n(s_n\overrightarrow{ a }),B_n(t_n\overrightarrow{ b }+\overrightarrow{ c })$
(nは正の整数)を定める。
(1)$s_n$を用いて$s_{n+1}$を表せ。
(2)極限値$S=\lim_{n \to \infty}s_n, T=\lim_{n \to \infty}t_n$を求めよ。
(3)(2)で求めたS,Tに対して、点A,Bをそれぞれ$A(S\overrightarrow{ a }),B(T\overrightarrow{ b }+\overrightarrow{ c })$とおくと、
直線ABは2直線l,l'の両方と直交することを示せ。
2022東北大学理系過去問
大学入試問題#149 岩手大学(2019) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{3}\displaystyle \frac{x}{(4-x)^3}\ dx$を計算せよ。
出典:2019年岩手大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{3}\displaystyle \frac{x}{(4-x)^3}\ dx$を計算せよ。
出典:2019年岩手大学 入試問題
福田の数学〜京都大学2022年文系第2問〜条件を満たす経路の総数と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
下図(※動画参照)の三角柱ABC-DEFにおいて、Aを始点として、辺に沿って
頂点をn回移動する。すなわち、この移動経路
$P_0 \to P_1 \to P_2 \to \ldots \to P_{n-1} \to P_n$ (ただし$P_0=A$)
において、$P_0P_1,P_1P_2,\ldots,P_{n-1}P_n$は全て辺であるとする。
また、同じ頂点を何度通ってよいものとする。このような移動経路で、終点$P_n$がA,B,Cの
いずれかとなるものの総数$a_n$を求めよ。
2022京都大学文系過去問
この動画を見る
下図(※動画参照)の三角柱ABC-DEFにおいて、Aを始点として、辺に沿って
頂点をn回移動する。すなわち、この移動経路
$P_0 \to P_1 \to P_2 \to \ldots \to P_{n-1} \to P_n$ (ただし$P_0=A$)
において、$P_0P_1,P_1P_2,\ldots,P_{n-1}P_n$は全て辺であるとする。
また、同じ頂点を何度通ってよいものとする。このような移動経路で、終点$P_n$がA,B,Cの
いずれかとなるものの総数$a_n$を求めよ。
2022京都大学文系過去問
大学入試問題#148 京都大学(1972) 積分と極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$F(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{t}{(t+1)(t+3)}dt$のとき
$\displaystyle \lim_{ x \to \infty }(F(x)-log\ x)$を求めよ。
出典:1972年京都大学 入試問題
この動画を見る
$x \gt 0$
$F(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{t}{(t+1)(t+3)}dt$のとき
$\displaystyle \lim_{ x \to \infty }(F(x)-log\ x)$を求めよ。
出典:1972年京都大学 入試問題
