 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜明治大学2021年全学部統一入試IⅡAB第1問(3)〜九九の表の平均と分散

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)九九の表(1の段から9の段まで)に現れる81個の数の平均値$\boxed{\ \ シス\ \ }$であり、
分散は小数第一位を四捨五入して整数で求めると$\boxed{\ \ セソタ\ \ }$である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{1}}$(3)九九の表(1の段から9の段まで)に現れる81個の数の平均値$\boxed{\ \ シス\ \ }$であり、
分散は小数第一位を四捨五入して整数で求めると$\boxed{\ \ セソタ\ \ }$である。
2021明治大学全統過去問
福田の数学〜明治大学2021年全学部統一入試IⅡAB第1問(2)〜位置ベクトルと面積比

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)三角形ABC内に点Pがあり、$3\overrightarrow{ PA }+5\ \overrightarrow{ PB }+7\ \overrightarrow{ PC }=\overrightarrow{ 0 }$のとき、
$\overrightarrow{ AP }=\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\overrightarrow{ AB }+\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケコ\ \ }}\overrightarrow{ AC }$
となるので、$\triangle PAB :\triangle PBC :\triangle PCA=\boxed{\ \ サ\ \ }$である。
$\boxed{\ \ サ\ \ }$の解答群
$⓪1:1:1 ①3:5:7 ②5:7:3 ③7:3:5 ④9:25:49$
$⑤25:49:9 ⑥49:9:25 ⑦\frac{1}{3}:\frac{1}{5}:\frac{1}{7} ⑧\frac{1}{5}:\frac{1}{7}:\frac{1}{3} ⑨\frac{1}{7}:\frac{1}{3}:\frac{1}{5}$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{1}}$(2)三角形ABC内に点Pがあり、$3\overrightarrow{ PA }+5\ \overrightarrow{ PB }+7\ \overrightarrow{ PC }=\overrightarrow{ 0 }$のとき、
$\overrightarrow{ AP }=\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\overrightarrow{ AB }+\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケコ\ \ }}\overrightarrow{ AC }$
となるので、$\triangle PAB :\triangle PBC :\triangle PCA=\boxed{\ \ サ\ \ }$である。
$\boxed{\ \ サ\ \ }$の解答群
$⓪1:1:1 ①3:5:7 ②5:7:3 ③7:3:5 ④9:25:49$
$⑤25:49:9 ⑥49:9:25 ⑦\frac{1}{3}:\frac{1}{5}:\frac{1}{7} ⑧\frac{1}{5}:\frac{1}{7}:\frac{1}{3} ⑨\frac{1}{7}:\frac{1}{3}:\frac{1}{5}$
2021明治大学全統過去問
数学「大学入試良問集」【19−15 ガウス記号と極限・区分求積法】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
実数$x$に対して、$x$を越えない最大の整数を$\lbrack x \rbrack$で表す。
$n$を正の整数とし、$a_n=\displaystyle \sum_{k=1}^n\displaystyle \frac{\lbrack \sqrt{ 2n^2-k^2 } \rbrack}{n^2}$とおく。
このとき、$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
この動画を見る
実数$x$に対して、$x$を越えない最大の整数を$\lbrack x \rbrack$で表す。
$n$を正の整数とし、$a_n=\displaystyle \sum_{k=1}^n\displaystyle \frac{\lbrack \sqrt{ 2n^2-k^2 } \rbrack}{n^2}$とおく。
このとき、$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
【理数個別の過去問解説】2004年度京都大学 数学 第3問解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
京都大学(文系)2004年(第3問)
$△OAB$において、$a=OA、b=OB$とし、$\vert a\vert =3, \vert b\vert =5, cos\angle AOB=\dfrac{3}{5}$とする。このとき、$\angle AOB$の二等分線とBを中心とする半径$\sqrt{10}$の円との交点の、Oを原点とする位置ベクトルを、a, bを用いて表せ。
この動画を見る
京都大学(文系)2004年(第3問)
$△OAB$において、$a=OA、b=OB$とし、$\vert a\vert =3, \vert b\vert =5, cos\angle AOB=\dfrac{3}{5}$とする。このとき、$\angle AOB$の二等分線とBを中心とする半径$\sqrt{10}$の円との交点の、Oを原点とする位置ベクトルを、a, bを用いて表せ。
福田の数学〜明治大学2021年全学部統一入試IⅡAB第1問(1)〜連立型の漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)数列$\left\{a_n\right\},\ \left\{b_n\right\}$について次の条件が与えられている。
$\left\{
\begin{array}{1}
a_{n+1}=7a_n-10b_n\\
b_{n+1}=2a_n-2b_n
\end{array}
\right. (n=1,2,3,\ldots)$
ただし、$a_1=11,\ b_1=4$とする。このとき、
$\left\{
\begin{array}{1}
c_n=a_n-2b_n \\
d_n=2a_n-5b_n
\end{array}
\right. (n=1,2,3,\ldots)$
とおくと、$c_n=\boxed{\ \ ア\ \ }^n, d_n=\boxed{\ \ イ\ \ }^n$であり、これより$\left\{a_n\right\},\ \left\{b_n\right\}$
の一般項は
$\left\{
\begin{array}{1}
a_n=\boxed{\ \ ウ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ エ\ \ }・\boxed{\ \ イ\ \ }^n\\
b_n=\boxed{\ \ オ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ イ\ \ }^n \\
\end{array}
\right.$
である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{1}}$(1)数列$\left\{a_n\right\},\ \left\{b_n\right\}$について次の条件が与えられている。
$\left\{
\begin{array}{1}
a_{n+1}=7a_n-10b_n\\
b_{n+1}=2a_n-2b_n
\end{array}
\right. (n=1,2,3,\ldots)$
ただし、$a_1=11,\ b_1=4$とする。このとき、
$\left\{
\begin{array}{1}
c_n=a_n-2b_n \\
d_n=2a_n-5b_n
\end{array}
\right. (n=1,2,3,\ldots)$
とおくと、$c_n=\boxed{\ \ ア\ \ }^n, d_n=\boxed{\ \ イ\ \ }^n$であり、これより$\left\{a_n\right\},\ \left\{b_n\right\}$
の一般項は
$\left\{
\begin{array}{1}
a_n=\boxed{\ \ ウ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ エ\ \ }・\boxed{\ \ イ\ \ }^n\\
b_n=\boxed{\ \ オ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ イ\ \ }^n \\
\end{array}
\right.$
である。
2021明治大学全統過去問
【数C】平面ベクトル:角の二等分線上の位置ベクトル(神戸大学)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
平面上に原点Oから出る、相異なる2本の半直線OX、OY(∠XOY<180°)上にそれぞれOと異なる2点A,Bをとる。
(1)a=OA, b=OBとする。点Cが∠XOYの二等分線上にあるとき、OCを実数t(t≧0)とa, bで表せ。
(2)∠XOYの二等分線と∠XABの二等分線の交点をPとする。OA=2, B=3, AB=4のとき、OPをa, bで表せ。
この動画を見る
平面上に原点Oから出る、相異なる2本の半直線OX、OY(∠XOY<180°)上にそれぞれOと異なる2点A,Bをとる。
(1)a=OA, b=OBとする。点Cが∠XOYの二等分線上にあるとき、OCを実数t(t≧0)とa, bで表せ。
(2)∠XOYの二等分線と∠XABの二等分線の交点をPとする。OA=2, B=3, AB=4のとき、OPをa, bで表せ。
数学「大学入試良問集」【19−14 サイクロイドと接線・面積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#武蔵工業大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
サイクロイド$x=\theta-\sin\theta,y=1-\cos\theta(0 \leqq \theta \leqq 2\pi)$
次の各問いに答えよ。
(1)$C$上の点$\lbrack \displaystyle \frac{\pi}{2}-1,1 \rbrack$における接線$l$の方程式を求めよ。
(2)接線$l$と$y$軸および$C$で囲まれた部分の面積を求めよ。
この動画を見る
サイクロイド$x=\theta-\sin\theta,y=1-\cos\theta(0 \leqq \theta \leqq 2\pi)$
次の各問いに答えよ。
(1)$C$上の点$\lbrack \displaystyle \frac{\pi}{2}-1,1 \rbrack$における接線$l$の方程式を求めよ。
(2)接線$l$と$y$軸および$C$で囲まれた部分の面積を求めよ。
福田の数学〜青山学院大学2021年理工学部第5問〜絶対値の付いた関数と面積の最大最小

単元:
#大学入試過去問(数学)#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$tを$0 \leqq t \leqq \frac{\pi}{2}$を満たす定数とする。関数
$f(x)=|\sin x-\sin t| (0 \leqq x \leqq \pi)$
について、以下の問いに答えよ。
(1)$t=\frac{\pi}{6}$のとき$y=f(x) (0 \leqq x \leqq \pi)$のグラフを描け。
(2)$y=f(x) (0 \leqq x \leqq \pi)$のグラフとx軸、y軸および直線$x=\pi$
で囲まれた図形の面積をSとする。Sをtを用いて表せ。
(3)tが$\leqq t \leqq \frac{\pi}{2}$の範囲を動くときのSの最大値と最小値を求めよ。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{5}}$tを$0 \leqq t \leqq \frac{\pi}{2}$を満たす定数とする。関数
$f(x)=|\sin x-\sin t| (0 \leqq x \leqq \pi)$
について、以下の問いに答えよ。
(1)$t=\frac{\pi}{6}$のとき$y=f(x) (0 \leqq x \leqq \pi)$のグラフを描け。
(2)$y=f(x) (0 \leqq x \leqq \pi)$のグラフとx軸、y軸および直線$x=\pi$
で囲まれた図形の面積をSとする。Sをtを用いて表せ。
(3)tが$\leqq t \leqq \frac{\pi}{2}$の範囲を動くときのSの最大値と最小値を求めよ。
2021青山学院大学理工学部過去問
数学「大学入試良問集」【19−13媒介変数表示のグラフと面積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
媒介変数$t$を用いて$x=1-\cos\ t,y=1+t\ \sin\ t+\cos\ t(0 \leqq t \leqq \pi)$と表される座標平面上の曲線を$C$とする。
このとき、次の各問いに答えよ。
(1)$y$の最大値と最小値を求めよ。
(2)曲線$C,x$軸および$y$軸で囲まれる部分の面積$S$を求めよ。
この動画を見る
媒介変数$t$を用いて$x=1-\cos\ t,y=1+t\ \sin\ t+\cos\ t(0 \leqq t \leqq \pi)$と表される座標平面上の曲線を$C$とする。
このとき、次の各問いに答えよ。
(1)$y$の最大値と最小値を求めよ。
(2)曲線$C,x$軸および$y$軸で囲まれる部分の面積$S$を求めよ。
【数Ⅱ】微分法と積分法:一橋大学1989年 角度の最大

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線$C:y=x^3$上の点$P(a,a^3)(a\gt 0)$における接線をlとし、lが再びCと交わる点をQとする。また、QにおけるCの接線をmとし、lとmがなす角を$\theta(0\lt\theta\lt \dfrac{\pi}{2})$とする。
(1)$\tan\theta$をaを用いて表せ。
(2)aが正の実数値をとりながら変化するとき、$\theta$を最大にするaの値、および、そのときの$\tan\theta$の値を求めよう。
この動画を見る
曲線$C:y=x^3$上の点$P(a,a^3)(a\gt 0)$における接線をlとし、lが再びCと交わる点をQとする。また、QにおけるCの接線をmとし、lとmがなす角を$\theta(0\lt\theta\lt \dfrac{\pi}{2})$とする。
(1)$\tan\theta$をaを用いて表せ。
(2)aが正の実数値をとりながら変化するとき、$\theta$を最大にするaの値、および、そのときの$\tan\theta$の値を求めよう。
福田の数学〜青山学院大学2021年理工学部第4問〜複素数平面上の点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$複素数平面上の点zが$z+\bar{ z }=2$を満たしながら動くとき、以下の問いに答えよ。
(1)点z全体が描く図形を複素数平面上に図示せよ。
(2)$w=(2+i)z$ で定まる点w全体が描く図形を調べよう。
$(\textrm{a})w$の実部をu、虚部をvとして$w=u+vi$と表すとき、u,vが満たす方程式
を求めよ。
$(\textrm{b})$点w全体が描く図形を複素数平面上に図示せよ。
(3)$w=z^2$で定まる点w全体が描く図形を複素数平面上に図示せよ。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{4}}$複素数平面上の点zが$z+\bar{ z }=2$を満たしながら動くとき、以下の問いに答えよ。
(1)点z全体が描く図形を複素数平面上に図示せよ。
(2)$w=(2+i)z$ で定まる点w全体が描く図形を調べよう。
$(\textrm{a})w$の実部をu、虚部をvとして$w=u+vi$と表すとき、u,vが満たす方程式
を求めよ。
$(\textrm{b})$点w全体が描く図形を複素数平面上に図示せよ。
(3)$w=z^2$で定まる点w全体が描く図形を複素数平面上に図示せよ。
2021青山学院大学理工学部過去問
【数Ⅱ】等式の証明:解と係数の関係の利用(防衛大学校)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#防衛大学校#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a\neq b, b\neq c, c\neq a$のとき、$a, b, c$が$ \dfrac{a^3+2a}{a+1} = \dfrac{b^3+2b}{b+1} = \dfrac{c^3+2c}{c+1} = k$ を満たすならば、次の各等式が成り立つことを証明せよ。
(1)$a+b+c=0$。
(2)$k=abc$
この動画を見る
$a\neq b, b\neq c, c\neq a$のとき、$a, b, c$が$ \dfrac{a^3+2a}{a+1} = \dfrac{b^3+2b}{b+1} = \dfrac{c^3+2c}{c+1} = k$ を満たすならば、次の各等式が成り立つことを証明せよ。
(1)$a+b+c=0$。
(2)$k=abc$
数学「大学入試良問集」【19−12 (sinx)^nの積分と漸化式の作成】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
自然数$n$に対して、定積分$I_n$を$I_n=\displaystyle \int_{0}^{\frac{\pi}{4}}\sin^nx\ dx$で定める。
$n \geqq 3$のとき、$I_n$を$I_{n-2}$と$n$を用いて表せ。
また、$I_2・I_4$の値を求めよ。
この動画を見る
自然数$n$に対して、定積分$I_n$を$I_n=\displaystyle \int_{0}^{\frac{\pi}{4}}\sin^nx\ dx$で定める。
$n \geqq 3$のとき、$I_n$を$I_{n-2}$と$n$を用いて表せ。
また、$I_2・I_4$の値を求めよ。
福田の数学〜青山学院大学2021年理工学部第3問〜領域における最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ 連立方程式
$\left\{
\begin{array}{1}
0 \leqq y \leqq 6 \\
y \geqq -x+7 \\
y \leqq -2x+14
\end{array}
\right.\\
$
の表す領域をDとする。
(1)領域Dを図示せよ。
(2)点$(x,\ y)$が領域Dを動くとき、$3x+2y$の最大値と最小値を求めよ。
(3)点$(x,\ y)$が領域Dを動くとき、$x^2-6x+2y$の最大値と最小値を求めよ。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$ 連立方程式
$\left\{
\begin{array}{1}
0 \leqq y \leqq 6 \\
y \geqq -x+7 \\
y \leqq -2x+14
\end{array}
\right.\\
$
の表す領域をDとする。
(1)領域Dを図示せよ。
(2)点$(x,\ y)$が領域Dを動くとき、$3x+2y$の最大値と最小値を求めよ。
(3)点$(x,\ y)$が領域Dを動くとき、$x^2-6x+2y$の最大値と最小値を求めよ。
2021青山学院大学理工学部過去問
数学「大学入試良問集」【19−11 面積の極限とネイピア数】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#京都産業大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
曲線$C:y=\displaystyle \frac{1}{x}(x \gt 0)$を考える。
また、$n=1,2,3,・・・$と正の実数$t$に対し、曲線$C_n:y=-\displaystyle \frac{n}{x}+t(x \gt 0)$を考える。
次の各問いに答えよ。
(1)
$C$と$C_n$が1点$P(a,b)$で交わり、$P$における$C$と$C_n$の接線が直行するとき、$a$と$t$を$n$を用いて表せ。
(2)
(1)のとき、曲線$C_n$と$P$における$C$の接線、および$x$軸とで囲まれる図形の面積$S_n$を求めよ。
(3)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
この動画を見る
曲線$C:y=\displaystyle \frac{1}{x}(x \gt 0)$を考える。
また、$n=1,2,3,・・・$と正の実数$t$に対し、曲線$C_n:y=-\displaystyle \frac{n}{x}+t(x \gt 0)$を考える。
次の各問いに答えよ。
(1)
$C$と$C_n$が1点$P(a,b)$で交わり、$P$における$C$と$C_n$の接線が直行するとき、$a$と$t$を$n$を用いて表せ。
(2)
(1)のとき、曲線$C_n$と$P$における$C$の接線、および$x$軸とで囲まれる図形の面積$S_n$を求めよ。
(3)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
福田の数学〜青山学院大学2021年理工学部第2問〜平面ベクトルとベクトル方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$ 平面上に3点O,A,Bがあり、
$|\overrightarrow{ OA }|=|\sqrt2\overrightarrow{ OA }+\overrightarrow{ OB }|=|2\sqrt2\overrightarrow{ OA }+\overrightarrow{ OB }|=1$
を満たしている。
(1)$|\overrightarrow{ OB }|=\sqrt{\boxed{\ \ ア\ \ }}$
(2)$\cos\angle AOB=\frac{\boxed{\ \ イウ\ \ }\sqrt{\boxed{\ \ エオ\ \ }}}{\boxed{\ \ カキ\ \ }}$
(3)実数s,tが
$s \geqq 0,\ t \geqq 0,\ s+2t \leqq 1$
を満たしながら変化するとき、
$\overrightarrow{ OP }=s\ \overrightarrow{ OA }+t\ \overrightarrow{ OB }$
で定まる点Pの存在する範囲の面積は$\frac{\sqrt{\boxed{\ \ ク\ \ }}}{\boxed{\ \ ケ\ \ }}$
である。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$ 平面上に3点O,A,Bがあり、
$|\overrightarrow{ OA }|=|\sqrt2\overrightarrow{ OA }+\overrightarrow{ OB }|=|2\sqrt2\overrightarrow{ OA }+\overrightarrow{ OB }|=1$
を満たしている。
(1)$|\overrightarrow{ OB }|=\sqrt{\boxed{\ \ ア\ \ }}$
(2)$\cos\angle AOB=\frac{\boxed{\ \ イウ\ \ }\sqrt{\boxed{\ \ エオ\ \ }}}{\boxed{\ \ カキ\ \ }}$
(3)実数s,tが
$s \geqq 0,\ t \geqq 0,\ s+2t \leqq 1$
を満たしながら変化するとき、
$\overrightarrow{ OP }=s\ \overrightarrow{ OA }+t\ \overrightarrow{ OB }$
で定まる点Pの存在する範囲の面積は$\frac{\sqrt{\boxed{\ \ ク\ \ }}}{\boxed{\ \ ケ\ \ }}$
である。
2021青山学院大学理工学部過去問
福田の数学〜青山学院大学2021年理工学部第1問〜さいころの目の最大最小の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$1個のさいころを4回投げるとき、出た目の最小値をm、最大値をMとする。
(1)$m \geqq 2$となる確率は$\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカキ\ \ }}$であり、
$m=1$となる確率は$\frac{\boxed{\ \ クケコ\ \ }}{\boxed{\ \ サシスセ\ \ }}$である。
(2)$m \geqq 2$かつ$M \leqq 5$となる確率は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$であり、$m \geqq 2$かつ$M=6$となる確率は
$\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニヌ\ \ }}$である。
(3)$m=1$かつ$M=6$となる確率は$\frac{\boxed{\ \ ネノハ\ \ }}{\boxed{\ \ ヒフヘ\ \ }}$である。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$1個のさいころを4回投げるとき、出た目の最小値をm、最大値をMとする。
(1)$m \geqq 2$となる確率は$\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカキ\ \ }}$であり、
$m=1$となる確率は$\frac{\boxed{\ \ クケコ\ \ }}{\boxed{\ \ サシスセ\ \ }}$である。
(2)$m \geqq 2$かつ$M \leqq 5$となる確率は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$であり、$m \geqq 2$かつ$M=6$となる確率は
$\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニヌ\ \ }}$である。
(3)$m=1$かつ$M=6$となる確率は$\frac{\boxed{\ \ ネノハ\ \ }}{\boxed{\ \ ヒフヘ\ \ }}$である。
2021青山学院大学理工学部過去問
数学「大学入試良問集」【19−10 指数関数の微分と面積の最大最小】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#同志社大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
定数$a(1 \lt a \lt 2)$に対して、曲線$y=a^x$上の点$(t,a^t)(0 \leqq t \leqq 1)$における接線を$l$とする。
次の問いに答えよ。
(1)
接線$l$の方程式を求めよ。
また、$l$と$y$軸の交点を$(0,b(t))$とし、$b(t)$の最小値を$a$で表せ。
(2)
接線$l$と$x$軸および2直線$x=0,x=1$で囲まれた台形の面積$S(t)$を求めよ。
(3)
$S(t)$の最大値を$a$で表せ。
(4)
$S(t)$の最小値を$a$で表せ。
この動画を見る
定数$a(1 \lt a \lt 2)$に対して、曲線$y=a^x$上の点$(t,a^t)(0 \leqq t \leqq 1)$における接線を$l$とする。
次の問いに答えよ。
(1)
接線$l$の方程式を求めよ。
また、$l$と$y$軸の交点を$(0,b(t))$とし、$b(t)$の最小値を$a$で表せ。
(2)
接線$l$と$x$軸および2直線$x=0,x=1$で囲まれた台形の面積$S(t)$を求めよ。
(3)
$S(t)$の最大値を$a$で表せ。
(4)
$S(t)$の最小値を$a$で表せ。
福田の数学〜上智大学2021年TEAP利用理系第4問〜楕円と弦の中点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#軌跡と領域#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$Oを原点とする座標平面において、楕円$D:\frac{x^2}{6}+\frac{y^2}{2}=1$ 上に異なる2点$P_1,P_2$
がある。$P_1$における接線$l_1$と$P_2$における接線$l_2$の交点を$Q(a,\ b)$とし、線分$P_1P_2$の
中点をRとする。
(1)$P_1$の座標を$(x_1,\ y_1)$とするとき、$l_1$の方程式は$x_1x+\boxed{\ \ チ\ \ }\ y_1y+\boxed{\ \ ツ\ \ }=0$
と表される。
(2)直線$P_1P_2$の方程式は、a,bを用いて$ax+\boxed{\ \ テ\ \ }\ by+\boxed{\ \ ト\ \ }=0$と表される。
(3)3点O,R,Qは一直線上にあって$\overrightarrow{ OR }=\frac{\boxed{\ \ ナ\ \ }}{a^2+\boxed{\ \ ニ\ \ }\ b^2}\overrightarrow{ OQ }$が成り立つ。
(4)$l_1$と$l_2$のどちらもy軸と平行ではないとする。このとき、$l_1$と$l_2$の傾きは
tの方程式$(a^2+\boxed{\ \ ヌ\ \ })t^2+\boxed{\ \ ネ\ \ }abt+(b^2+\boxed{\ \ ノ\ \ })=0$ の解である。
(5)$l_1$と$l_2$が直交しながら$P_1,P_2$が動くとする。
$(\textrm{i})Q$の軌跡の方程式を求めよ。 $(\textrm{ii})R$のy座標の最大値を求めよ。
$(\textrm{iii})R$の軌跡の概形を描け。
2021上智大学理系過去問
この動画を見る
${\Large\boxed{4}}$Oを原点とする座標平面において、楕円$D:\frac{x^2}{6}+\frac{y^2}{2}=1$ 上に異なる2点$P_1,P_2$
がある。$P_1$における接線$l_1$と$P_2$における接線$l_2$の交点を$Q(a,\ b)$とし、線分$P_1P_2$の
中点をRとする。
(1)$P_1$の座標を$(x_1,\ y_1)$とするとき、$l_1$の方程式は$x_1x+\boxed{\ \ チ\ \ }\ y_1y+\boxed{\ \ ツ\ \ }=0$
と表される。
(2)直線$P_1P_2$の方程式は、a,bを用いて$ax+\boxed{\ \ テ\ \ }\ by+\boxed{\ \ ト\ \ }=0$と表される。
(3)3点O,R,Qは一直線上にあって$\overrightarrow{ OR }=\frac{\boxed{\ \ ナ\ \ }}{a^2+\boxed{\ \ ニ\ \ }\ b^2}\overrightarrow{ OQ }$が成り立つ。
(4)$l_1$と$l_2$のどちらもy軸と平行ではないとする。このとき、$l_1$と$l_2$の傾きは
tの方程式$(a^2+\boxed{\ \ ヌ\ \ })t^2+\boxed{\ \ ネ\ \ }abt+(b^2+\boxed{\ \ ノ\ \ })=0$ の解である。
(5)$l_1$と$l_2$が直交しながら$P_1,P_2$が動くとする。
$(\textrm{i})Q$の軌跡の方程式を求めよ。 $(\textrm{ii})R$のy座標の最大値を求めよ。
$(\textrm{iii})R$の軌跡の概形を描け。
2021上智大学理系過去問
福田の数学〜上智大学2021年TEAP利用理系第3問〜複雑な試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$南北方向にm区画、東西方向にn区画に区切られた長方形の土地がある。
この土地のそれぞれの区画にm種類の作物を1種類ずつ植える。ただし、南北方向に
は同じ種類の作物が植えられている区画はないようにする。このとき、東西方向に
隣り合う区画に同じ種類の作物が植えられている場合には、それらの区画は連結
した1個の畑とみなすとする。例えば、南北方向に3区画、東西方向に5区画で、
A,B,C3種類の作物を次のように植えた場合、畑が11個とみなす。
(1)$m=3$の時を考える。$n=1$ならば、畑の数は常に3個で、1通りある。
$n=2$ならば、畑の数は3個、5個、6個で3通りある。$n=3$ならば、畑の数は
$\boxed{\ \ ク\ \ }$通りある。$n=10$ならば、畑の数は$\boxed{\ \ ケ\ \ }$通りある。
(2)$m=3$で$n=3$のとき、畑の数が8個になる植え方は$\boxed{\ \ コ\ \ }$通りある。
(3)$m=6$のときを考える。各列の南北方向の6区画に作物を植える植え方は6!通り
あるが、それらすべてが等確率になるように植えることにする。$n=2$のとき、
畑が8個である確率は$\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}$であり、畑が9個である確率は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
畑が10個である確率は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。$n=3$のとき、
畑が10個である確率をpとすると$\boxed{\ \ け\ \ }$である。
$\boxed{\ \ け\ \ }$の選択肢:
$(\textrm{a})p \geqq \frac{1}{100} (\textrm{b})\frac{1}{200} \leqq p \lt \frac{1}{100} (\textrm{c})\frac{1}{500} \leqq p \lt \frac{1}{200}$
$(\textrm{d})\frac{1}{1000} \leqq p \lt \frac{1}{500} (\textrm{e})\frac{1}{2000} \leqq p \lt \frac{1}{1000} (\textrm{f})\frac{1}{5000} \leqq p \lt \frac{1}{2000}$
$(\textrm{g})\frac{1}{10000} \leqq p \lt \frac{1}{5000} (\textrm{h})p \lt \frac{1}{10000}$
2021上智大学理系過去問
この動画を見る
${\Large\boxed{3}}$南北方向にm区画、東西方向にn区画に区切られた長方形の土地がある。
この土地のそれぞれの区画にm種類の作物を1種類ずつ植える。ただし、南北方向に
は同じ種類の作物が植えられている区画はないようにする。このとき、東西方向に
隣り合う区画に同じ種類の作物が植えられている場合には、それらの区画は連結
した1個の畑とみなすとする。例えば、南北方向に3区画、東西方向に5区画で、
A,B,C3種類の作物を次のように植えた場合、畑が11個とみなす。
(1)$m=3$の時を考える。$n=1$ならば、畑の数は常に3個で、1通りある。
$n=2$ならば、畑の数は3個、5個、6個で3通りある。$n=3$ならば、畑の数は
$\boxed{\ \ ク\ \ }$通りある。$n=10$ならば、畑の数は$\boxed{\ \ ケ\ \ }$通りある。
(2)$m=3$で$n=3$のとき、畑の数が8個になる植え方は$\boxed{\ \ コ\ \ }$通りある。
(3)$m=6$のときを考える。各列の南北方向の6区画に作物を植える植え方は6!通り
あるが、それらすべてが等確率になるように植えることにする。$n=2$のとき、
畑が8個である確率は$\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}$であり、畑が9個である確率は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
畑が10個である確率は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。$n=3$のとき、
畑が10個である確率をpとすると$\boxed{\ \ け\ \ }$である。
$\boxed{\ \ け\ \ }$の選択肢:
$(\textrm{a})p \geqq \frac{1}{100} (\textrm{b})\frac{1}{200} \leqq p \lt \frac{1}{100} (\textrm{c})\frac{1}{500} \leqq p \lt \frac{1}{200}$
$(\textrm{d})\frac{1}{1000} \leqq p \lt \frac{1}{500} (\textrm{e})\frac{1}{2000} \leqq p \lt \frac{1}{1000} (\textrm{f})\frac{1}{5000} \leqq p \lt \frac{1}{2000}$
$(\textrm{g})\frac{1}{10000} \leqq p \lt \frac{1}{5000} (\textrm{h})p \lt \frac{1}{10000}$
2021上智大学理系過去問
福田の数学〜上智大学2021年TEAP利用理系第2問〜集合の要素と包含関係

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#集合と命題(集合・命題と条件・背理法)#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$実数からなる集合A,B,Cを次のように定義する。ただし、$a \gt 0$
$A=\left\{x |\ |x| \lt a \right\}$
$B=\left\{x |\ (x+2)(x-5)(x^2+2x-7) \leqq 0 \right\}$
$C=\left\{x |\ 3^{\frac{x}{3}} \leqq \frac{1}{3}(x+4) \right\}$
(1)$A \cap B$が空集合であるための必要十分条件は$a \boxed{\ \ お\ \ } \ \boxed{\ \ \alpha\ \ }$である。
(2)$A \supset B$であるための必要十分条件は$a \boxed{\ \ か\ \ } \ \boxed{\ \ \beta\ \ }$である。
$\boxed{\ \ お\ \ },\ \boxed{\ \ か\ \ }$の選択肢$:(\textrm{a})= (\textrm{b})\lt (\textrm{c})\leqq (\textrm{d})\gt (\textrm{e})\geqq (\textrm{f})\neq$
$\boxed{\ \ \alpha\ \ },\ \boxed{\ \ \beta\ \ }$の選択肢$:(\textrm{a})1 (\textrm{b})2 (\textrm{c})3 (\textrm{d})5 (\textrm{e})7 (\textrm{f})10$
($\textrm{g})-1+2\sqrt2 (\textrm{h})1+2\sqrt2 (\textrm{i})-2+\sqrt7 (\textrm{j})2+\sqrt7$
(3)$-1 \boxed{\ \ き\ \ }C$であり、$5 \boxed{\ \ く\ \ }C$である。
$\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ }$の選択肢$:(\textrm{a})\in (\textrm{b})\notin (\textrm{c})\ni (\textrm{d})∋ (\textrm{e})= (\textrm{f})\subset (\textrm{g})\supset$
(4)Cに属する整数は$\boxed{\ \ オ\ \ }$個ある。
(5)$A \subset C$となるaのうち、整数で最大のものは$\boxed{\ \ カ\ \ }$である。
(6)$A \supset C$となるaのうち、整数で最小のものは$\boxed{\ \ キ\ \ }$である。
2021上智大学理系過去問
この動画を見る
${\Large\boxed{2}}$実数からなる集合A,B,Cを次のように定義する。ただし、$a \gt 0$
$A=\left\{x |\ |x| \lt a \right\}$
$B=\left\{x |\ (x+2)(x-5)(x^2+2x-7) \leqq 0 \right\}$
$C=\left\{x |\ 3^{\frac{x}{3}} \leqq \frac{1}{3}(x+4) \right\}$
(1)$A \cap B$が空集合であるための必要十分条件は$a \boxed{\ \ お\ \ } \ \boxed{\ \ \alpha\ \ }$である。
(2)$A \supset B$であるための必要十分条件は$a \boxed{\ \ か\ \ } \ \boxed{\ \ \beta\ \ }$である。
$\boxed{\ \ お\ \ },\ \boxed{\ \ か\ \ }$の選択肢$:(\textrm{a})= (\textrm{b})\lt (\textrm{c})\leqq (\textrm{d})\gt (\textrm{e})\geqq (\textrm{f})\neq$
$\boxed{\ \ \alpha\ \ },\ \boxed{\ \ \beta\ \ }$の選択肢$:(\textrm{a})1 (\textrm{b})2 (\textrm{c})3 (\textrm{d})5 (\textrm{e})7 (\textrm{f})10$
($\textrm{g})-1+2\sqrt2 (\textrm{h})1+2\sqrt2 (\textrm{i})-2+\sqrt7 (\textrm{j})2+\sqrt7$
(3)$-1 \boxed{\ \ き\ \ }C$であり、$5 \boxed{\ \ く\ \ }C$である。
$\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ }$の選択肢$:(\textrm{a})\in (\textrm{b})\notin (\textrm{c})\ni (\textrm{d})∋ (\textrm{e})= (\textrm{f})\subset (\textrm{g})\supset$
(4)Cに属する整数は$\boxed{\ \ オ\ \ }$個ある。
(5)$A \subset C$となるaのうち、整数で最大のものは$\boxed{\ \ カ\ \ }$である。
(6)$A \supset C$となるaのうち、整数で最小のものは$\boxed{\ \ キ\ \ }$である。
2021上智大学理系過去問
福田の数学〜上智大学2021年TEAP利用理系第1問(3)〜非回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (3)不等式
$1 \leqq z \leqq 4,\ \frac{x^2}{z^2}+4z^4y^2 \leqq 1$
が表す座標空間内の領域の体積は$\boxed{\ \ え\ \ }$である。
$\boxed{\ \ え\ \ }$の選択肢:
$(\textrm{a})\frac{3\pi}{2} (\textrm{b})3\pi (\textrm{c})\frac{3\pi^2}{2} (\textrm{d})3\pi^2$
$(\textrm{e})\pi\log 2 (\textrm{f})\frac{\pi\log 2}{2} (\textrm{g})3\pi^2\log 2$
2021上智大学理系過去問
この動画を見る
${\Large\boxed{1}}$ (3)不等式
$1 \leqq z \leqq 4,\ \frac{x^2}{z^2}+4z^4y^2 \leqq 1$
が表す座標空間内の領域の体積は$\boxed{\ \ え\ \ }$である。
$\boxed{\ \ え\ \ }$の選択肢:
$(\textrm{a})\frac{3\pi}{2} (\textrm{b})3\pi (\textrm{c})\frac{3\pi^2}{2} (\textrm{d})3\pi^2$
$(\textrm{e})\pi\log 2 (\textrm{f})\frac{\pi\log 2}{2} (\textrm{g})3\pi^2\log 2$
2021上智大学理系過去問
福田の数学〜上智大学2021年TEAP利用理系第1問(2)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)nを20以上の整数とする。n進法で表したとき、$n^3$の位の数が$1,n^2$の位の数が2,
$n^1$の位の数が$3,n^0$の位の数が0である数$1230_{(n)}$を$n+1$進法で表すと$(n+1)^2$の位
の数は$\boxed{\ \ あ\ \ }$であり、$(n+1)^1$の位の数は$\boxed{\ \ い\ \ }$であり、$(n+1)^0$の位の数は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }\ ~\ \boxed{\ \ う\ \ }$の選択肢:
$(\textrm{a})0 (\textrm{b})1 (\textrm{c})2 (\textrm{d})3$
$(\textrm{e})n-2 (\textrm{f})n-3 (\textrm{g})n-1 (\textrm{g})n$
2021上智大学理系過去問
この動画を見る
${\Large\boxed{1}}$(2)nを20以上の整数とする。n進法で表したとき、$n^3$の位の数が$1,n^2$の位の数が2,
$n^1$の位の数が$3,n^0$の位の数が0である数$1230_{(n)}$を$n+1$進法で表すと$(n+1)^2$の位
の数は$\boxed{\ \ あ\ \ }$であり、$(n+1)^1$の位の数は$\boxed{\ \ い\ \ }$であり、$(n+1)^0$の位の数は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }\ ~\ \boxed{\ \ う\ \ }$の選択肢:
$(\textrm{a})0 (\textrm{b})1 (\textrm{c})2 (\textrm{d})3$
$(\textrm{e})n-2 (\textrm{f})n-3 (\textrm{g})n-1 (\textrm{g})n$
2021上智大学理系過去問
大学入試問題#924「定場の問題」 #岡山県立大学2023

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} (8\cos^4-8\cos^2 x+1)dx$
を解け.
2023岡山県立大学過去問題
この動画を見る
$\displaystyle \int_{}^{} (8\cos^4-8\cos^2 x+1)dx$
を解け.
2023岡山県立大学過去問題
#関西大学2024#不定積分_36
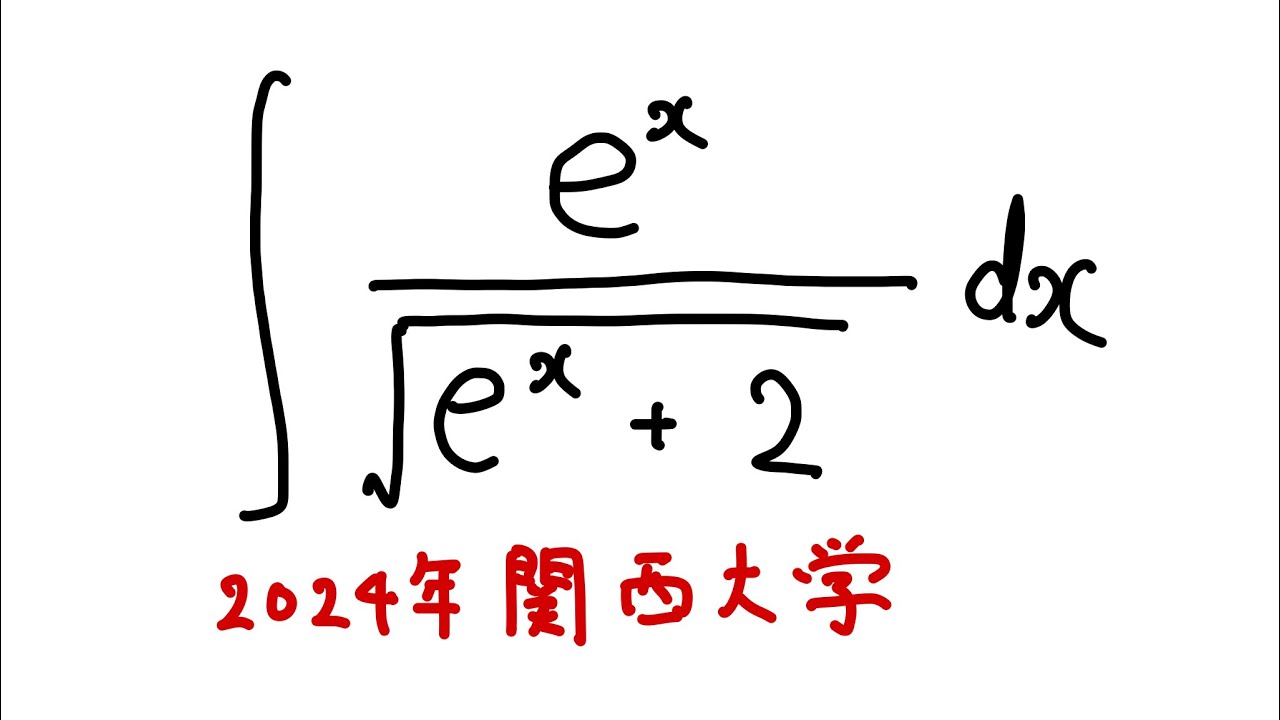
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \dfrac{e^x}{\sqrt{e^x+2}}dx$
を解け.
2024関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{e^x}{\sqrt{e^x+2}}dx$
を解け.
2024関西大学過去問題
福田の数学〜上智大学2021年TEAP利用理系第1問(1)〜偽陽性偽陰性の条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)ある病原菌の検査薬は、病原菌に感染しているのに誤って陰性と判断する
確率が20%、感染していないのに、誤って陽性と判断する確率が10%である。
全体の20%がこの病原菌に感染している集団から1つの検体を取り出して、
独立に2回、検査薬で検査する。こんとき、2回とも陰性であったが、実際には
感染している確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、少なくとも1回は陽性であったが、
実際には病原菌には感染していない確率は$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
2021上智大学理系過去問
この動画を見る
${\Large\boxed{1}}$(1)ある病原菌の検査薬は、病原菌に感染しているのに誤って陰性と判断する
確率が20%、感染していないのに、誤って陽性と判断する確率が10%である。
全体の20%がこの病原菌に感染している集団から1つの検体を取り出して、
独立に2回、検査薬で検査する。こんとき、2回とも陰性であったが、実際には
感染している確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、少なくとも1回は陽性であったが、
実際には病原菌には感染していない確率は$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
2021上智大学理系過去問
#関西大学2024#不定積分_35

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \dfrac{x^3+2x}{x^2+1} dx$
を解け.
2024関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^3+2x}{x^2+1} dx$
を解け.
2024関西大学過去問題
数学「大学入試良問集」【19−9 定積分と不等式の証明】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#和歌山大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の各問いに答えよ。
(1)
$0 \leqq x \leqq \displaystyle \frac{\pi}{2}$のとき、次の不等式が成り立つことを証明せよ。
$\displaystyle \frac{2x}{\pi} \leqq \sin\ x$
(2)
次の不等式が成り立つことを証明せよ。
$\displaystyle \int_{0}^{\pi}e^{-\sin\ x}dx \leqq \pi\left[ 1-\dfrac{ 1 }{ e } \right]$
この動画を見る
次の各問いに答えよ。
(1)
$0 \leqq x \leqq \displaystyle \frac{\pi}{2}$のとき、次の不等式が成り立つことを証明せよ。
$\displaystyle \frac{2x}{\pi} \leqq \sin\ x$
(2)
次の不等式が成り立つことを証明せよ。
$\displaystyle \int_{0}^{\pi}e^{-\sin\ x}dx \leqq \pi\left[ 1-\dfrac{ 1 }{ e } \right]$
福田の数学〜上智大学2021年TEAP利用文系第4問(2)〜線形計画法

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$(2)野菜Aには1個あたり栄養素$x_1$が8g、栄養素$x_2$が4g、栄養素$x_3$が2g
含まれ、野菜Bには1個あたり栄養素$x_1$が4g、栄養素$x_2$が6g、栄養素$x_3$
が6g含まれている。これら2種類の野菜をそれぞれ何個かずつ選んで
ミックスし野菜ジュースを作る。選んだ野菜は丸ごと全て用い、栄養素$x_1$
を42g以上、栄養素$x_2$を48g以上、栄養素$x_3$を30g以上含まれるように
したい。野菜Aの個数と野菜Bの個数の和をなるべく小さくしてジュース
を作るとき、野菜Aの個数a、野菜Bの個数bの組(a,\ b)は
$(a,\ b)=(\boxed{\ \ ヘ\ \ },\ \boxed{\ \ ホ\ \ }), (\boxed{\ \ マ\ \ },\ \boxed{\ \ ミ\ \ })$
である。ただし、 $\boxed{\ \ ヘ\ \ } \lt \boxed{\ \ マ\ \ }$とする。
2021上智大学文系過去問
この動画を見る
${\Large\boxed{4}}$(2)野菜Aには1個あたり栄養素$x_1$が8g、栄養素$x_2$が4g、栄養素$x_3$が2g
含まれ、野菜Bには1個あたり栄養素$x_1$が4g、栄養素$x_2$が6g、栄養素$x_3$
が6g含まれている。これら2種類の野菜をそれぞれ何個かずつ選んで
ミックスし野菜ジュースを作る。選んだ野菜は丸ごと全て用い、栄養素$x_1$
を42g以上、栄養素$x_2$を48g以上、栄養素$x_3$を30g以上含まれるように
したい。野菜Aの個数と野菜Bの個数の和をなるべく小さくしてジュース
を作るとき、野菜Aの個数a、野菜Bの個数bの組(a,\ b)は
$(a,\ b)=(\boxed{\ \ ヘ\ \ },\ \boxed{\ \ ホ\ \ }), (\boxed{\ \ マ\ \ },\ \boxed{\ \ ミ\ \ })$
である。ただし、 $\boxed{\ \ ヘ\ \ } \lt \boxed{\ \ マ\ \ }$とする。
2021上智大学文系過去問
【高校数学】日本大学の過去問演習~指数・対数の問題~【大学受験】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
日本大学の過去問演習 指数・対数の問題の解説動画です
この動画を見る
日本大学の過去問演習 指数・対数の問題の解説動画です
