立教大学
立教大学
福田の数学〜立教大学2025理学部第3問〜指数関数と円でできる領域の面積
単元：
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$a,p$は正の実数とする。
座標平面上の曲線$C_1:y=e^x$と$C_1$上の点
$(p,e^p)$がある。
$P$における$C_1$の法線を$\ell,\ell$と$x$軸の
交点を$A(a,0)$、$A$を中心とする半径$r$の円を
$C_2$とする。
$P$が$C_1$と$C_2$のただ一つの共有点であるとき、
次の問いに答えよ。
(1)$\ell$の方程式を$p$を用いて表せ。
(2)$a$を$p$を用いて表せ。
(3)$r$を$p$を用いて表せ。
(4)$\angle OAP=\dfrac{\pi}{6}$のとき、$p$の値を求めよ。
(5)$p$を(4)で求めた値とするとき、
次の不等式の表す領域$D$の面積$S$を求めよ。
$-2 \leqq x \leqq p,\ y\geqq 0,\ y\leqq e^x,$
$(x-a)^2+y^2\geqq r^2$
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{3}$
$a,p$は正の実数とする。
座標平面上の曲線$C_1:y=e^x$と$C_1$上の点
$(p,e^p)$がある。
$P$における$C_1$の法線を$\ell,\ell$と$x$軸の
交点を$A(a,0)$、$A$を中心とする半径$r$の円を
$C_2$とする。
$P$が$C_1$と$C_2$のただ一つの共有点であるとき、
次の問いに答えよ。
(1)$\ell$の方程式を$p$を用いて表せ。
(2)$a$を$p$を用いて表せ。
(3)$r$を$p$を用いて表せ。
(4)$\angle OAP=\dfrac{\pi}{6}$のとき、$p$の値を求めよ。
(5)$p$を(4)で求めた値とするとき、
次の不等式の表す領域$D$の面積$S$を求めよ。
$-2 \leqq x \leqq p,\ y\geqq 0,\ y\leqq e^x,$
$(x-a)^2+y^2\geqq r^2$
$2025$年立教大学理学部過去問題
福田の数学〜立教大学2025理学部第2問〜三角関数の最大最小の定番
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
福田の数学〜立教大学2025理学部第1問(4)〜確率の基本的な性質
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)箱の中に緑色のカードが$5$枚、
黄色のカードが$4$枚、赤色のカードが$3$枚
入っている。
箱から無作為にカードを$3$枚取り出すとき、
$3$枚とも同じ色である確率は$\boxed{オ}$、
$3$枚の色がすべて異なる確率は$\boxed{カ}$、
$2$枚が同じ色であり、かつ、
残りの$1$枚が他の$2$枚と異なる色である確率は
$\boxed{キ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(4)箱の中に緑色のカードが$5$枚、
黄色のカードが$4$枚、赤色のカードが$3$枚
入っている。
箱から無作為にカードを$3$枚取り出すとき、
$3$枚とも同じ色である確率は$\boxed{オ}$、
$3$枚の色がすべて異なる確率は$\boxed{カ}$、
$2$枚が同じ色であり、かつ、
残りの$1$枚が他の$2$枚と異なる色である確率は
$\boxed{キ}$である。
$2025$年立教大学理学部過去問題
福田の数学〜立教大学2025理学部第1問(3)〜定積分の計算
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)定積分$\displaystyle \int_{0}^{\frac{7}{6}\pi}\sin x \sin 2x \ dx$の値は
$\boxed{エ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(3)定積分$\displaystyle \int_{0}^{\frac{7}{6}\pi}\sin x \sin 2x \ dx$の値は
$\boxed{エ}$である。
$2025$年立教大学理学部過去問題
福田の数学〜立教大学2025理学部第1問(2)〜内積と絶対値の計算問題
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)$2$つの平面ベクトル$\overrightarrow{a},\overrightarrow{b}$は、
$\vert \overrightarrow{a}+\overrightarrow{b} \vert=4,\vert \overrightarrow{a}-\overrightarrow{b} \vert =2$を満たすとする。
このとき、内積$\overrightarrow{a}･\overrightarrow{b}$の値は$\boxed{イ}$である。
また、$\vert 2\overrightarrow{a}-3\overrightarrow{b} \vert^2+\vert 3 \overrightarrow{a}-2\overrightarrow{b} \vert^2$の値は$\boxed{ウ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(2)$2$つの平面ベクトル$\overrightarrow{a},\overrightarrow{b}$は、
$\vert \overrightarrow{a}+\overrightarrow{b} \vert=4,\vert \overrightarrow{a}-\overrightarrow{b} \vert =2$を満たすとする。
このとき、内積$\overrightarrow{a}･\overrightarrow{b}$の値は$\boxed{イ}$である。
また、$\vert 2\overrightarrow{a}-3\overrightarrow{b} \vert^2+\vert 3 \overrightarrow{a}-2\overrightarrow{b} \vert^2$の値は$\boxed{ウ}$である。
$2025$年立教大学理学部過去問題
福田の数学〜立教大学2025理学部第1問(1)〜不等式と対数
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)自然数$n$に対して$a_n=2^n$とし、
積$a_1a_2\cdots a_n$を$A_n$とおく。
このとき、$A_n \geqq 10^{10}$を満たす最小の
$n$は$\boxed{ア}$である。
ただし、$\log_2 10=3.3219$とする。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(1)自然数$n$に対して$a_n=2^n$とし、
積$a_1a_2\cdots a_n$を$A_n$とおく。
このとき、$A_n \geqq 10^{10}$を満たす最小の
$n$は$\boxed{ア}$である。
ただし、$\log_2 10=3.3219$とする。
$2025$年立教大学理学部過去問題
福田の数学〜立教大学2025経済学部第3問〜3次関数のグラフと直線の共有点の個数
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$k$を実数とする。
$3$次関数$f(x)=x^3-x^2+1$に対して、
座標平面上の曲線$C$を$C:y=f(x)$とする。
また、$C$上の点$P(1,1)$を通り、
傾きが$k$である直線を$\ell$とする。
このとき、次の問いに答えよ。
(1)$\ell$の方程式を$k$を用いて表せ。
(2)$f(x)$の導関数$f'(x)$を求めよ。
(3)$f(x)$の極値を求めよ。
また、そのときの$x$の値を求めよ。
(4)$\ell$と$C$がちょうど$2$個の共有点を
もつような$k$の値を求めよ。
(5)$\ell$と$C$が異なる$3$個の共有点をもつような
$k$の値の範囲を求めよ。
(6)(5)のとき、異なる$3$個の共有点の$y$座標を
小さい方から順に$y_1,y_2,y_3$とする。
このとき、
比の等式$(y_2-y_1):(y_3-y_2)=1:2$を
満たすような$k$の値を求めよ。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{3}$
$k$を実数とする。
$3$次関数$f(x)=x^3-x^2+1$に対して、
座標平面上の曲線$C$を$C:y=f(x)$とする。
また、$C$上の点$P(1,1)$を通り、
傾きが$k$である直線を$\ell$とする。
このとき、次の問いに答えよ。
(1)$\ell$の方程式を$k$を用いて表せ。
(2)$f(x)$の導関数$f'(x)$を求めよ。
(3)$f(x)$の極値を求めよ。
また、そのときの$x$の値を求めよ。
(4)$\ell$と$C$がちょうど$2$個の共有点を
もつような$k$の値を求めよ。
(5)$\ell$と$C$が異なる$3$個の共有点をもつような
$k$の値の範囲を求めよ。
(6)(5)のとき、異なる$3$個の共有点の$y$座標を
小さい方から順に$y_1,y_2,y_3$とする。
このとき、
比の等式$(y_2-y_1):(y_3-y_2)=1:2$を
満たすような$k$の値を求めよ。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第2問〜2点の位置関係と三角関数
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$p,q$を正の実数とする。
原点を$O$とする座標平面上に
点$A(1,0)$、点$P\left(p,\dfrac{1}{p}\right)$,点$Q\left(q,\dfrac{2}{q}\right)$がある。
$\angle AOP=\alpha,\angle AOQ=\beta$とおき、
$P,Q$は$\alpha \lt \beta$を満たしながら動くものとする。
三角形$OPQ$の面積を$S$とし、
また、$T=\tan(\beta-\alpha)$とおく。
(1)$\cos\alpha,\sin\alpha$をそれぞれ$p$を用いて表せ。
また、$\cos\beta,\sin\beta$をそれぞれ$q$を用いて表せ。
(2)$T$を$p,q$を用いて表せ。
(3)$S$を$p,q$を用いて表せ。
(4)$t=pq$とおく。$\dfrac{S}{T}$を$t$を用いて表せ。
(5)$\dfrac{S}{T}$の最小値を求めよ。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{2}$
$p,q$を正の実数とする。
原点を$O$とする座標平面上に
点$A(1,0)$、点$P\left(p,\dfrac{1}{p}\right)$,点$Q\left(q,\dfrac{2}{q}\right)$がある。
$\angle AOP=\alpha,\angle AOQ=\beta$とおき、
$P,Q$は$\alpha \lt \beta$を満たしながら動くものとする。
三角形$OPQ$の面積を$S$とし、
また、$T=\tan(\beta-\alpha)$とおく。
(1)$\cos\alpha,\sin\alpha$をそれぞれ$p$を用いて表せ。
また、$\cos\beta,\sin\beta$をそれぞれ$q$を用いて表せ。
(2)$T$を$p,q$を用いて表せ。
(3)$S$を$p,q$を用いて表せ。
(4)$t=pq$とおく。$\dfrac{S}{T}$を$t$を用いて表せ。
(5)$\dfrac{S}{T}$の最小値を求めよ。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第1問(6)〜2つのベクトルの両方に垂直なベクトル
単元：
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(6)空間のベクトル$\vec{ p}=(x,y,z)$は
$\vec{b}=(0,3,2)$の両方に垂直であり、
$\vec{\vert p \vert}=7$かつ$z \gt 0$を
満たしている。
このとき、$\vec{p}=(\boxed{ク},\boxed{ケ},\boxed{コ})$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(6)空間のベクトル$\vec{ p}=(x,y,z)$は
$\vec{b}=(0,3,2)$の両方に垂直であり、
$\vec{\vert p \vert}=7$かつ$z \gt 0$を
満たしている。
このとき、$\vec{p}=(\boxed{ク},\boxed{ケ},\boxed{コ})$である。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第1問(5)〜絶対値の付いた関数の定積分の計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(5)定積分$\displaystyle \int_{0}^{2} (x+1)\vert x-1 \vert dx$
の値は$\boxed{キ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(5)定積分$\displaystyle \int_{0}^{2} (x+1)\vert x-1 \vert dx$
の値は$\boxed{キ}$である。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第1問(4)〜2直線が1点で交わる条件
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)実数$a$は定数とする。
座標平面上の$2$つの直線$(a+1)x+ay=1$
$ax+(a+2)y=2$がただ$1$つの交点を持つための
$a$の条件は$\boxed{カ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(4)実数$a$は定数とする。
座標平面上の$2$つの直線$(a+1)x+ay=1$
$ax+(a+2)y=2$がただ$1$つの交点を持つための
$a$の条件は$\boxed{カ}$である。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第1問(3)〜等差中項と等比中項
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)$x,y,z$は実数であり、$x\lt y$を満たすとする。
$3$つの数$3,x,y$がこの順に等差数列となり、
さらに$4$つの数$4,x,y,z$がこの順に
等差数列となるとき、
$x=\boxed{ウ}、\boxed{エ}、\boxed{オ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(3)$x,y,z$は実数であり、$x\lt y$を満たすとする。
$3$つの数$3,x,y$がこの順に等差数列となり、
さらに$4$つの数$4,x,y,z$がこの順に
等差数列となるとき、
$x=\boxed{ウ}、\boxed{エ}、\boxed{オ}$である。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第1問(2)〜順列と確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)赤玉$3$個と白玉$4$個を無作為に$1$列に
並べるとき、
白玉が両端にある確率は$\boxed{イ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(2)赤玉$3$個と白玉$4$個を無作為に$1$列に
並べるとき、
白玉が両端にある確率は$\boxed{イ}$である。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第1問(1)〜指数不等式
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2024年経済学部第1問(4)〜三角関数の計算
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \theta = \frac{\pi}{12}$ のとき、$\displaystyle \frac{1}{\tan \theta} - \tan \theta$ の値は $\fbox{キ}$ である。
この動画を見る
$\displaystyle \theta = \frac{\pi}{12}$ のとき、$\displaystyle \frac{1}{\tan \theta} - \tan \theta$ の値は $\fbox{キ}$ である。
福田の数学〜立教大学2024年経済学部第3問〜ベクトルと平面幾何
単元：
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
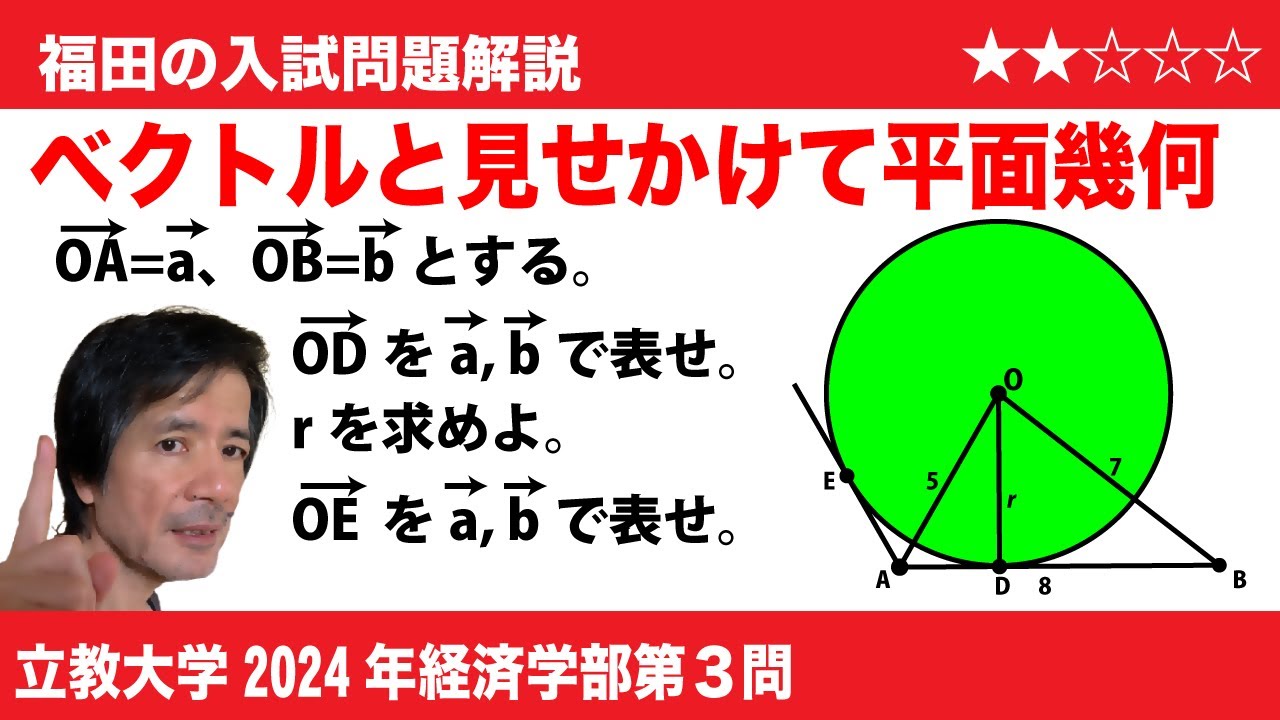
三角形$\mathrm{OAB}$において、$\mathrm{OA}=5,\mathrm{OB}=7,\mathrm{AB}=8$とする。また、$\mathrm{O}$を中心とする半径$r$の円$C$が直線$\mathrm{AB}$上の点$\mathrm{D}$で接している。さらに、$\mathrm{A}$から$C$へ引いた接線と$C$との接点を$\mathrm{E}$とする。ただし、$\mathrm{E}$は$\mathrm{D}$と異なる点とする。$\overrightarrow{\mathrm{OA}}=\vec{a}, \overrightarrow{\mathrm{OB}}=\vec{b}$とおくとき、次の問いに答えよ。
(1) 内積$\vec{a}\cdot \vec{b}$を求めよ。
(2) $\overrightarrow{\mathrm{OD}}$を$\overrightarrow{\mathrm{OD}}=(1-t)\vec{a}+t\vec{b}$と表すとき、定数$t$の値を求めよ。
(3)$r$の値を求めよ。
(4) $\mathrm{D}$から$\mathrm{OA}$へ下した垂線を$\mathrm{DH}$とする。$\overrightarrow{\mathrm{DH}}$を$\vec{a}$を用いて表せ。
(5) $\mathrm{OE}$を$\mathrm{OE}=p\vec{a}+q\vec{b}$と表すとき、定数$p,q$の値を求めよ。
この動画を見る
三角形$\mathrm{OAB}$において、$\mathrm{OA}=5,\mathrm{OB}=7,\mathrm{AB}=8$とする。また、$\mathrm{O}$を中心とする半径$r$の円$C$が直線$\mathrm{AB}$上の点$\mathrm{D}$で接している。さらに、$\mathrm{A}$から$C$へ引いた接線と$C$との接点を$\mathrm{E}$とする。ただし、$\mathrm{E}$は$\mathrm{D}$と異なる点とする。$\overrightarrow{\mathrm{OA}}=\vec{a}, \overrightarrow{\mathrm{OB}}=\vec{b}$とおくとき、次の問いに答えよ。
(1) 内積$\vec{a}\cdot \vec{b}$を求めよ。
(2) $\overrightarrow{\mathrm{OD}}$を$\overrightarrow{\mathrm{OD}}=(1-t)\vec{a}+t\vec{b}$と表すとき、定数$t$の値を求めよ。
(3)$r$の値を求めよ。
(4) $\mathrm{D}$から$\mathrm{OA}$へ下した垂線を$\mathrm{DH}$とする。$\overrightarrow{\mathrm{DH}}$を$\vec{a}$を用いて表せ。
(5) $\mathrm{OE}$を$\mathrm{OE}=p\vec{a}+q\vec{b}$と表すとき、定数$p,q$の値を求めよ。
福田の数学〜立教大学2024年経済学部第2問〜接線が作る三角形の面積の最小値
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$p,q$を正の定数とする。座標平面上に放物線$C:y=-x^2$がある。$C$上の点$\mathrm{P}(p,-p^2)$における$C$の接線を$l$,$\mathrm{Q}(q,-q^2)$における$C$の接線を$m$とする。また$l$と$m$の交点を$\mathrm{R}$とする。
(1) $l,m$の方程式をそれぞれ求めよ。
(2) $\mathrm{R}$の座標を$p,q$を用いて表せ。
(3) $\mathrm{Q}$と$l$の距離$d$を$p,q$を用いて表せ。
(4) 三角形$\mathrm{PQR}$の面積$S$を$p,q$を用いて表せ。
(5) $l$と$m$が直交するとき、$q$を$p$を用いて表せ。
(6) $l$と$m$が直交するとき、(4)の$S$の最小値を求めよ。また、そのときの$p$の値を求めよ。
この動画を見る
$p,q$を正の定数とする。座標平面上に放物線$C:y=-x^2$がある。$C$上の点$\mathrm{P}(p,-p^2)$における$C$の接線を$l$,$\mathrm{Q}(q,-q^2)$における$C$の接線を$m$とする。また$l$と$m$の交点を$\mathrm{R}$とする。
(1) $l,m$の方程式をそれぞれ求めよ。
(2) $\mathrm{R}$の座標を$p,q$を用いて表せ。
(3) $\mathrm{Q}$と$l$の距離$d$を$p,q$を用いて表せ。
(4) 三角形$\mathrm{PQR}$の面積$S$を$p,q$を用いて表せ。
(5) $l$と$m$が直交するとき、$q$を$p$を用いて表せ。
(6) $l$と$m$が直交するとき、(4)の$S$の最小値を求めよ。また、そのときの$p$の値を求めよ。
福田の数学〜立教大学2024年経済学部第1問(6)〜定積分で表された関数
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$0 \leqq x \leqq1$ の範囲において $f(x) \geqq 0$ である $2$ 次関数 $f(x) = ax^2+b$ は、等式
$\displaystyle f(x)(\int_0^1f(t)dt) = x^2+5$
を満たす。このとき、定数 $a,b$ は $a=\fbox{ケ}, b=\fbox{コ}$ である。
この動画を見る
$0 \leqq x \leqq1$ の範囲において $f(x) \geqq 0$ である $2$ 次関数 $f(x) = ax^2+b$ は、等式
$\displaystyle f(x)(\int_0^1f(t)dt) = x^2+5$
を満たす。このとき、定数 $a,b$ は $a=\fbox{ケ}, b=\fbox{コ}$ である。
福田の数学〜立教大学2024年経済学部第1問(5)〜漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
初項と第 $2$ 項がそれぞれ $a_1=1,a_2=1$ であり数列 $\{a_n\}$ は、 $n \geqq 2$ のとき等式
$$a_{n+1}=a_1+a_2+ \cdots + a_n$$
を満たす。 $n \geqq 3$ のとき $a_n$ を $n$ を用いて表すと、 $a_n = \fbox{ク}$ である。
この動画を見る
初項と第 $2$ 項がそれぞれ $a_1=1,a_2=1$ であり数列 $\{a_n\}$ は、 $n \geqq 2$ のとき等式
$$a_{n+1}=a_1+a_2+ \cdots + a_n$$
を満たす。 $n \geqq 3$ のとき $a_n$ を $n$ を用いて表すと、 $a_n = \fbox{ク}$ である。
福田の数学〜立教大学2024年経済学部第1問(3)〜3回のさいころの目の積が4の倍数となる確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
さいころを $3$ 回投げて出る目をすべてかけた数が $4$ の倍数となる確率は $\fbox{カ}$ である。
この動画を見る
さいころを $3$ 回投げて出る目をすべてかけた数が $4$ の倍数となる確率は $\fbox{カ}$ である。
福田の数学〜立教大学2024年経済学部第1問(2)〜恒等式の未定係数を決定する方法
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
等式$\frac{3x^2-x+4}{(x+1)^3}=\frac{a}{(z+1)^3}+\frac{b}{(x+1)^2}+\frac{c}{x+1}$が$x$についての恒等式となるような定数$a, b, c$は$a=\fbox{ウ}, b=\fbox{エ}, c=\fbox{オ}$である。
この動画を見る
等式$\frac{3x^2-x+4}{(x+1)^3}=\frac{a}{(z+1)^3}+\frac{b}{(x+1)^2}+\frac{c}{x+1}$が$x$についての恒等式となるような定数$a, b, c$は$a=\fbox{ウ}, b=\fbox{エ}, c=\fbox{オ}$である。
福田の数学〜立教大学2024年経済学部第1問(1)〜対数関数の最小値
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1\leqq x\leqq 8$の範囲において、関数$y=(\log_{2} x)^2-8\log_{2} x-20$は$x=\fbox{ア}$のときに最小値$\fbox{イ}$をとる。
この動画を見る
$1\leqq x\leqq 8$の範囲において、関数$y=(\log_{2} x)^2-8\log_{2} x-20$は$x=\fbox{ア}$のときに最小値$\fbox{イ}$をとる。
福田の数学〜立教大学2024年理学部第4問〜3次方程式の実数解と整数解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$m, a, b, c, d, e, f, r, s, t$を自然数とする。このとき(1)~(5)に答えよ。ただし、(2)(3)の事実は(4)(5)で用いてよい。
(1)2次方程式$2x^2+5x+m=0$の解が有理数となるような自然数$m$をすべて求めよ。ただし、$p$が素数であるとき$\sqrt{p}$が無理数であることを用いてよい。
(2)3次方程式$x^3+ax^2+bx+c=0$の実数解は負の数であることを証明せよ。ただし、方程式$x^3+ax^2+bx+c=0$が少なくとも1つ実数解をもつことは証明せずに用いてよい。
(3)3次方程式$x^3+dx^2+ex+f=0$が整数$n$を解にもつとする。このとき$n$は$f$の約数であることを示せ。
(4)3次方程式$x^3+rx^2+rx+3=0$が整数解を少なくとも1つもつような自然数$r$をすべて求めよ。
(5)3次方程式$x^3+sx^2+tx+6=0$が異なる3つの整数を解にもつような自然数の組$(s, t)$をすべて求めよ。
この動画を見る
$m, a, b, c, d, e, f, r, s, t$を自然数とする。このとき(1)~(5)に答えよ。ただし、(2)(3)の事実は(4)(5)で用いてよい。
(1)2次方程式$2x^2+5x+m=0$の解が有理数となるような自然数$m$をすべて求めよ。ただし、$p$が素数であるとき$\sqrt{p}$が無理数であることを用いてよい。
(2)3次方程式$x^3+ax^2+bx+c=0$の実数解は負の数であることを証明せよ。ただし、方程式$x^3+ax^2+bx+c=0$が少なくとも1つ実数解をもつことは証明せずに用いてよい。
(3)3次方程式$x^3+dx^2+ex+f=0$が整数$n$を解にもつとする。このとき$n$は$f$の約数であることを示せ。
(4)3次方程式$x^3+rx^2+rx+3=0$が整数解を少なくとも1つもつような自然数$r$をすべて求めよ。
(5)3次方程式$x^3+sx^2+tx+6=0$が異なる3つの整数を解にもつような自然数の組$(s, t)$をすべて求めよ。
福田の数学〜立教大学2024年理学部第3問〜放物線のx軸周りとy軸周りの回転体の体積バームクーヘン積分
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}O$を原点とする座標平面上に放物線$C:y=x-x^2$がある。$C$上の点$P(\frac{1}{2},\frac{1}{4})$における$C$の接線を$l$、$Q(1,0)$における$C$の接線を$m$とする。$l$と$y$軸、$m$と$y$軸の交点をそれぞれR、Sとする。
(1)$l,m$の方程式をそれぞれ求めよ。
(2)$C$の$0\leqq x \leqq 1$の部分と、2つの線分QS,OSで囲まれた図形の面積Aを求めよ。
(3)$C$の$0 leqq x \leqq 1$の部分と、線分OQで囲まれた図形を、$x$軸のまわりに1回転させてできる立体の体積$V_1$を求めよ。
(4)$C$の$0 \leqq x \leqq \frac{1}{2}$の部分と、2つの線分PR,ORで囲まれた図形を、$y$軸のまわりに1回転させてできる立体$V_2$を求めよ。
(5)$C$の$0 \leqq x \leqq 1$の部分と、線分OQで囲まれた図形を、$y$軸のまわりに1回転させてできる立体の体積$V_3$を求めよ。
この動画を見る
$\boxed{3}O$を原点とする座標平面上に放物線$C:y=x-x^2$がある。$C$上の点$P(\frac{1}{2},\frac{1}{4})$における$C$の接線を$l$、$Q(1,0)$における$C$の接線を$m$とする。$l$と$y$軸、$m$と$y$軸の交点をそれぞれR、Sとする。
(1)$l,m$の方程式をそれぞれ求めよ。
(2)$C$の$0\leqq x \leqq 1$の部分と、2つの線分QS,OSで囲まれた図形の面積Aを求めよ。
(3)$C$の$0 leqq x \leqq 1$の部分と、線分OQで囲まれた図形を、$x$軸のまわりに1回転させてできる立体の体積$V_1$を求めよ。
(4)$C$の$0 \leqq x \leqq \frac{1}{2}$の部分と、2つの線分PR,ORで囲まれた図形を、$y$軸のまわりに1回転させてできる立体$V_2$を求めよ。
(5)$C$の$0 \leqq x \leqq 1$の部分と、線分OQで囲まれた図形を、$y$軸のまわりに1回転させてできる立体の体積$V_3$を求めよ。
福田の数学〜立教大学2024年理学部第1問(2)〜17のn乗の1の位
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
福田の数学〜立教大学2024年理学部第1問(1)〜三角方程式の基本
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{1}}$ (1)実数$x$が$3\cos x$=$\sin^2x$ を満たすとき、$\cos x$の値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (1)実数$x$が$3\cos x$=$\sin^2x$ を満たすとき、$\cos x$の値は$\boxed{\ \ ア\ \ }$である。
大学入試問題#860「これ、ええ問題」 #立教大学 #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin(1-\cos x)}{x^2}$
出典：立教大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin(1-\cos x)}{x^2}$
出典：立教大学 入試問題
#立教大学(2010) #定積分 #Shorts
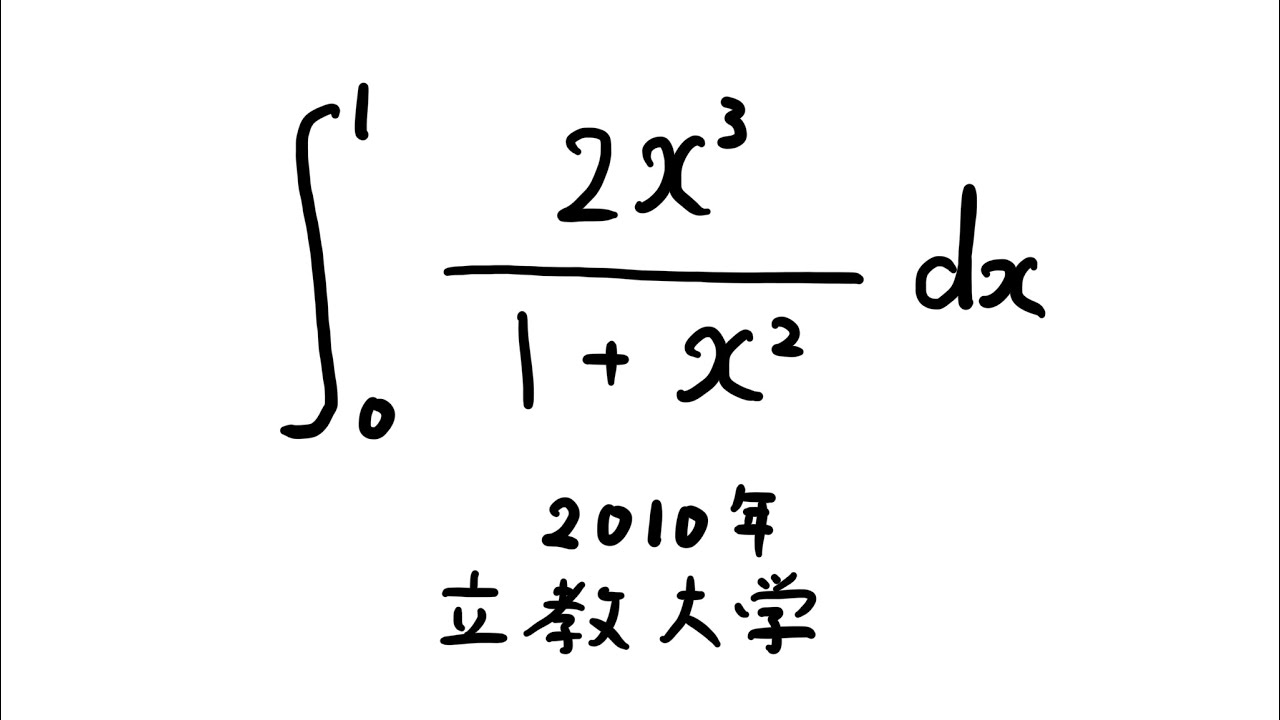
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x^3}{1+x^2} dx$
出典：2010年立教大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x^3}{1+x^2} dx$
出典：2010年立教大学
福田の数学〜立教大学2023年経済学部第3問〜放物線と直線で囲まれた図形の面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#学校別大学入試過去問解説(数学)#面積、体積#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
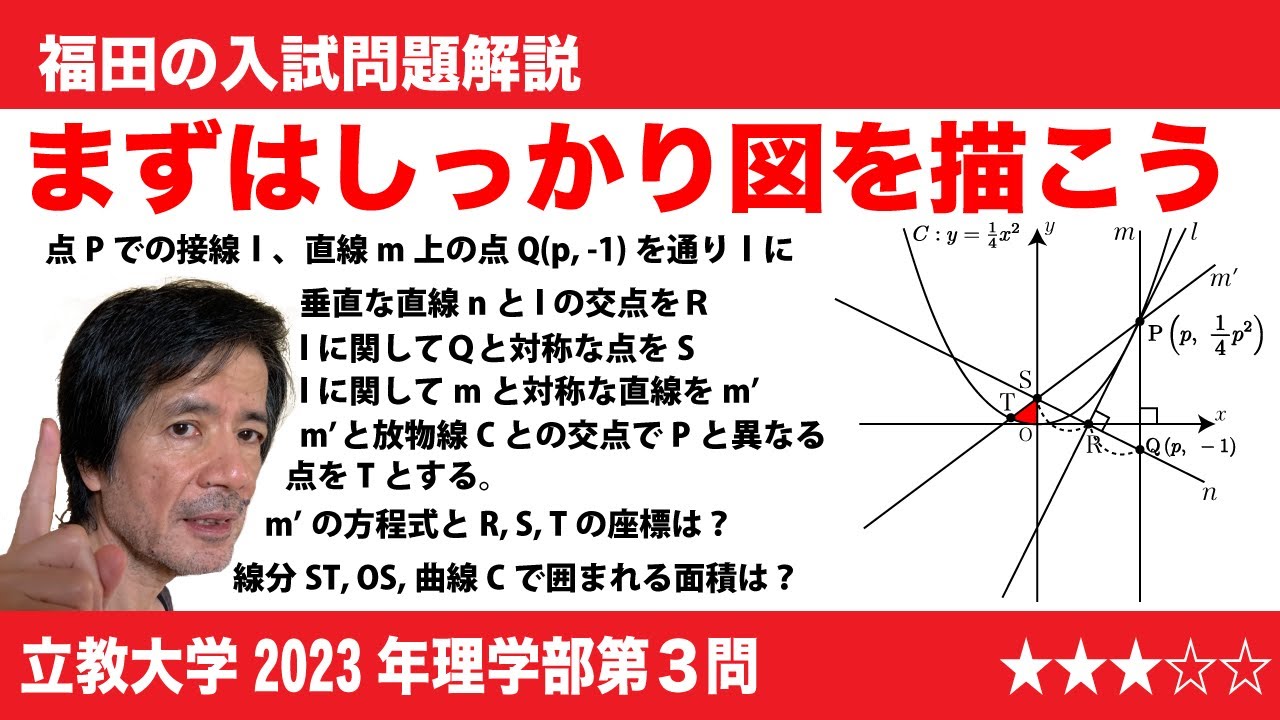
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C：$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
この動画を見る
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C：$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
福田の数学〜立教大学2023年経済学部第2問〜利息計算と漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 1年目の初めに新規に100万円を預金し、2年目以降の毎年初めに12万円を追加で預金する。ただし、毎年の終わりに、その時点での預金額の8%が利子として預金に加算される。自然数$n$に対して、$n$年目の終わりに利子が加算された後の預金額を$S_n$万円とする。このとき、以下の問いに答えよ。
ただし、$\log_{10}2$=0.3010, $\log_{10}3$=0.4771とする。
(1)$S_1$, $S_2$をそれぞれ求めよ。
(2)$S_{n+1}$を$S_n$を用いて表せ。
(3)$S_n$を$n$を用いて表せ。
(4)$\log_{10}1.08$を求めよ。
(5)$S_n$＞513 を満たす最小の自然数$n$を求めよ。
この動画を見る
$\Large\boxed{2}$ 1年目の初めに新規に100万円を預金し、2年目以降の毎年初めに12万円を追加で預金する。ただし、毎年の終わりに、その時点での預金額の8%が利子として預金に加算される。自然数$n$に対して、$n$年目の終わりに利子が加算された後の預金額を$S_n$万円とする。このとき、以下の問いに答えよ。
ただし、$\log_{10}2$=0.3010, $\log_{10}3$=0.4771とする。
(1)$S_1$, $S_2$をそれぞれ求めよ。
(2)$S_{n+1}$を$S_n$を用いて表せ。
(3)$S_n$を$n$を用いて表せ。
(4)$\log_{10}1.08$を求めよ。
(5)$S_n$＞513 を満たす最小の自然数$n$を求めよ。