 千葉大学
千葉大学
 千葉大学
千葉大学
福田の数学〜千葉大学2022年理系第6問〜独立に動く空間上の2点の距離の最小

単元:
#大学入試過去問(数学)#空間ベクトル#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、原点Oと点A(1,0,-1)と点B(0,5,0)がある。
実数$t$を用いて$t\ \overrightarrow{ OA }+\overrightarrow{ OB }$と表される点全体をlとする。また、平面xy平面上
の$y=x^2$を満たす点全体からなる曲線をCとする。
(1)曲線$C$上の点$P(a,a^2,0)$を固定する。l上の点Qを、$\overrightarrow{ OA }$と$\overrightarrow{ PQ }$
が垂直であるようにとる。このとき、点Qの座標をaを用いて表せ。
(2)曲線C上の点Rとl上の点Sのうち、$|\overrightarrow{ RS }|$を最小にする点Rと点Sの
組み合わせを全て求めよ。また、そのときの$|\overrightarrow{ RS }|$の値を求めよ。
2022千葉大学理系過去問
この動画を見る
座標空間において、原点Oと点A(1,0,-1)と点B(0,5,0)がある。
実数$t$を用いて$t\ \overrightarrow{ OA }+\overrightarrow{ OB }$と表される点全体をlとする。また、平面xy平面上
の$y=x^2$を満たす点全体からなる曲線をCとする。
(1)曲線$C$上の点$P(a,a^2,0)$を固定する。l上の点Qを、$\overrightarrow{ OA }$と$\overrightarrow{ PQ }$
が垂直であるようにとる。このとき、点Qの座標をaを用いて表せ。
(2)曲線C上の点Rとl上の点Sのうち、$|\overrightarrow{ RS }|$を最小にする点Rと点Sの
組み合わせを全て求めよ。また、そのときの$|\overrightarrow{ RS }|$の値を求めよ。
2022千葉大学理系過去問
福田の数学〜千葉大学2022年理系第5問〜n個のサイコロの目の積の確率

単元:
#計算と数の性質#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。n個のサイコロを同時に投げ、出た目の積をMとおく。
(1)Mが2でも3でも割り切れない確率を求めよ。
(2)Mが2で割り切れるが、3でも4でも割り切れない確率を求めよ。
(3)Mが4では割り切れるが、3では割り切れない確率を求めよ。
2022千葉大学理系過去問
この動画を見る
nを自然数とする。n個のサイコロを同時に投げ、出た目の積をMとおく。
(1)Mが2でも3でも割り切れない確率を求めよ。
(2)Mが2で割り切れるが、3でも4でも割り切れない確率を求めよ。
(3)Mが4では割り切れるが、3では割り切れない確率を求めよ。
2022千葉大学理系過去問
福田の数学〜千葉大学2022年理系第4問〜不定方程式とユークリッドの互除法

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
0以上9999以下の整数を4桁で表示し、以下の操作を行うこととする。
ただし、 4桁で表示するとは、整数が100以上999以下の場合は千の位の数字を0、
10以上99以下の場合は千の位と百の位の数字を0、1以上9以下の場合は
千の位と百の位と十の位の数字を0、そして0はどの位の数字も0とすることである。
操作:千の位の数字と十の位の数字を入れ換える。さらに、百の位の数字と
一の位の数字を入れ換える。
また、整数Lに対し、操作によって得られた整数を$\bar{ L }$と表す。
(1) Mを0以上9999以下の整数とし、$M=100x+y$のように整数$x, y (0 \leqq x \leqq 99,$
$ 0 \leqq y \leqq 99)$を用いて表す。操作によって得られた$\bar{ M }$ がMの
$\frac{2}{3}$倍に3を足した数 に等しいならば、
$-197x+298y = 9$が成り立つことを証明せよ。
(2) Nが0以上 9999 以下の整数ならば、操作によって
得られた整数$\bar{ N }$はNの$\frac{2}{3}$倍に1を足した数と等しくならないことを証明せよ。
2022千葉大学理系過去問
この動画を見る
0以上9999以下の整数を4桁で表示し、以下の操作を行うこととする。
ただし、 4桁で表示するとは、整数が100以上999以下の場合は千の位の数字を0、
10以上99以下の場合は千の位と百の位の数字を0、1以上9以下の場合は
千の位と百の位と十の位の数字を0、そして0はどの位の数字も0とすることである。
操作:千の位の数字と十の位の数字を入れ換える。さらに、百の位の数字と
一の位の数字を入れ換える。
また、整数Lに対し、操作によって得られた整数を$\bar{ L }$と表す。
(1) Mを0以上9999以下の整数とし、$M=100x+y$のように整数$x, y (0 \leqq x \leqq 99,$
$ 0 \leqq y \leqq 99)$を用いて表す。操作によって得られた$\bar{ M }$ がMの
$\frac{2}{3}$倍に3を足した数 に等しいならば、
$-197x+298y = 9$が成り立つことを証明せよ。
(2) Nが0以上 9999 以下の整数ならば、操作によって
得られた整数$\bar{ N }$はNの$\frac{2}{3}$倍に1を足した数と等しくならないことを証明せよ。
2022千葉大学理系過去問
福田の数学〜千葉大学2022年理系第3問〜折り返された放物線と直線の交点の個数と囲まれる面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の問いに答えよ。
(1)aを実数とする。$y=ax$のグラフと$y=x|x-2|$のグラフの交点の個数が
最大となる$a$の範囲を求めよ。
(2)$0 \leqq a \leqq 2$とする。$S(a)$を$y=ax$のグラフと$y=x|x-2|$のグラフで
囲まれる図形の面積とする。$S(a)$をaの式で表せ。
(3)(2)で求めた$S(a)$を最小にするaの値を求めよ。
2022千葉大学理系過去問
この動画を見る
次の問いに答えよ。
(1)aを実数とする。$y=ax$のグラフと$y=x|x-2|$のグラフの交点の個数が
最大となる$a$の範囲を求めよ。
(2)$0 \leqq a \leqq 2$とする。$S(a)$を$y=ax$のグラフと$y=x|x-2|$のグラフで
囲まれる図形の面積とする。$S(a)$をaの式で表せ。
(3)(2)で求めた$S(a)$を最小にするaの値を求めよ。
2022千葉大学理系過去問
福田の数学〜千葉大学2022年理系第2問〜三角形と三角比

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、原点Oと点A(1,0)と点B(0,1)がある。$0 \lt t \lt 1$に対し、
線分BO,OA,ABのそれぞれを$t:(1-t)$に内分する点をP,Q,Rとする。
(1)$\triangle PQR$の面積をtの式で表せ。
(2)$\triangle PQR$が二等辺三角形になるときのtの値を全て求めよ。
(3)$\theta = \angle RPQ$とする。(2)それぞれの場合に$\cos\theta$を求めよ。
2022千葉大学理系過去問
この動画を見る
座標平面において、原点Oと点A(1,0)と点B(0,1)がある。$0 \lt t \lt 1$に対し、
線分BO,OA,ABのそれぞれを$t:(1-t)$に内分する点をP,Q,Rとする。
(1)$\triangle PQR$の面積をtの式で表せ。
(2)$\triangle PQR$が二等辺三角形になるときのtの値を全て求めよ。
(3)$\theta = \angle RPQ$とする。(2)それぞれの場合に$\cos\theta$を求めよ。
2022千葉大学理系過去問
福田の数学〜九州大学2022年文系第3問〜高次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$k$を実数とし、整式f(x)を
$f(x)=x^4+6x^3-kx^2+2kx-64$
で定める。方程式$f(x)=0$が虚数解をもつとき、以下の問いに答えよ。
(1)f(x)は$x-2$で割り切れることを示せ。
(2)方程式$f(x)=0$は負の実数解をもつことを示せ。
(3)方程式$f(x)=0$の全ての実数解が整数であり、
すべての虚数解の実部と虚部が共に整数であるとする。
このような$k$を全て求めよ。
2022九州大学文系過去問
この動画を見る
$k$を実数とし、整式f(x)を
$f(x)=x^4+6x^3-kx^2+2kx-64$
で定める。方程式$f(x)=0$が虚数解をもつとき、以下の問いに答えよ。
(1)f(x)は$x-2$で割り切れることを示せ。
(2)方程式$f(x)=0$は負の実数解をもつことを示せ。
(3)方程式$f(x)=0$の全ての実数解が整数であり、
すべての虚数解の実部と虚部が共に整数であるとする。
このような$k$を全て求めよ。
2022九州大学文系過去問
素数を扱え!整数問題【数学 入試問題】【千葉大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$p$は奇数である素数とし、$N=(p+1)(p+3)(p+5)$とおく。
(1)$N$は$48$の倍数であることを示せ。
(2)$N$は$144$の倍数になるような$p$の値を小さい順に$3$つ求めよ。
千葉大過去問
この動画を見る
$p$は奇数である素数とし、$N=(p+1)(p+3)(p+5)$とおく。
(1)$N$は$48$の倍数であることを示せ。
(2)$N$は$144$の倍数になるような$p$の値を小さい順に$3$つ求めよ。
千葉大過去問
福田の数学〜千葉大学2022年理系第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
円周を12等分するように点$A_1,A_2,A_3,\ldots,A_{12}$が時計回りに並んでいる。
また、白球2個と黒球4個が入った袋がある。点Pを、次の操作によって
12個の点上を移動させる。
操作:袋から球を一つ取り出した後にサイコロを投げる。白球ならば時計回りに、
黒球ならば反時計回りに、サイコロの目の数だけPを移動させる。
取り出した球は袋に戻さないこととする。
Pを最初に点 $A_1$に置く。操作を1回行い、Pが$A_1$から移動した点をQとおく。
続けて操作を1回行い、PがQから移動した点をRとおく。
もう一度操作を行い、 PがRから移動した点をSとおく。
(1) $R=A_1$となる確率を求めよ。
(2)3点Q, R, Sを結んでできる図形が正三角形となる確率を求めよ。
2022千葉大学理系過去問
この動画を見る
円周を12等分するように点$A_1,A_2,A_3,\ldots,A_{12}$が時計回りに並んでいる。
また、白球2個と黒球4個が入った袋がある。点Pを、次の操作によって
12個の点上を移動させる。
操作:袋から球を一つ取り出した後にサイコロを投げる。白球ならば時計回りに、
黒球ならば反時計回りに、サイコロの目の数だけPを移動させる。
取り出した球は袋に戻さないこととする。
Pを最初に点 $A_1$に置く。操作を1回行い、Pが$A_1$から移動した点をQとおく。
続けて操作を1回行い、PがQから移動した点をRとおく。
もう一度操作を行い、 PがRから移動した点をSとおく。
(1) $R=A_1$となる確率を求めよ。
(2)3点Q, R, Sを結んでできる図形が正三角形となる確率を求めよ。
2022千葉大学理系過去問
整数問題 千葉大(医)類題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$k,n$を
$k^2=3^n+360$
全て求めよ。
千葉大(医)過去問
この動画を見る
整数$k,n$を
$k^2=3^n+360$
全て求めよ。
千葉大(医)過去問
大学入試問題#98 千葉大学医学部(2018) 積分・極限
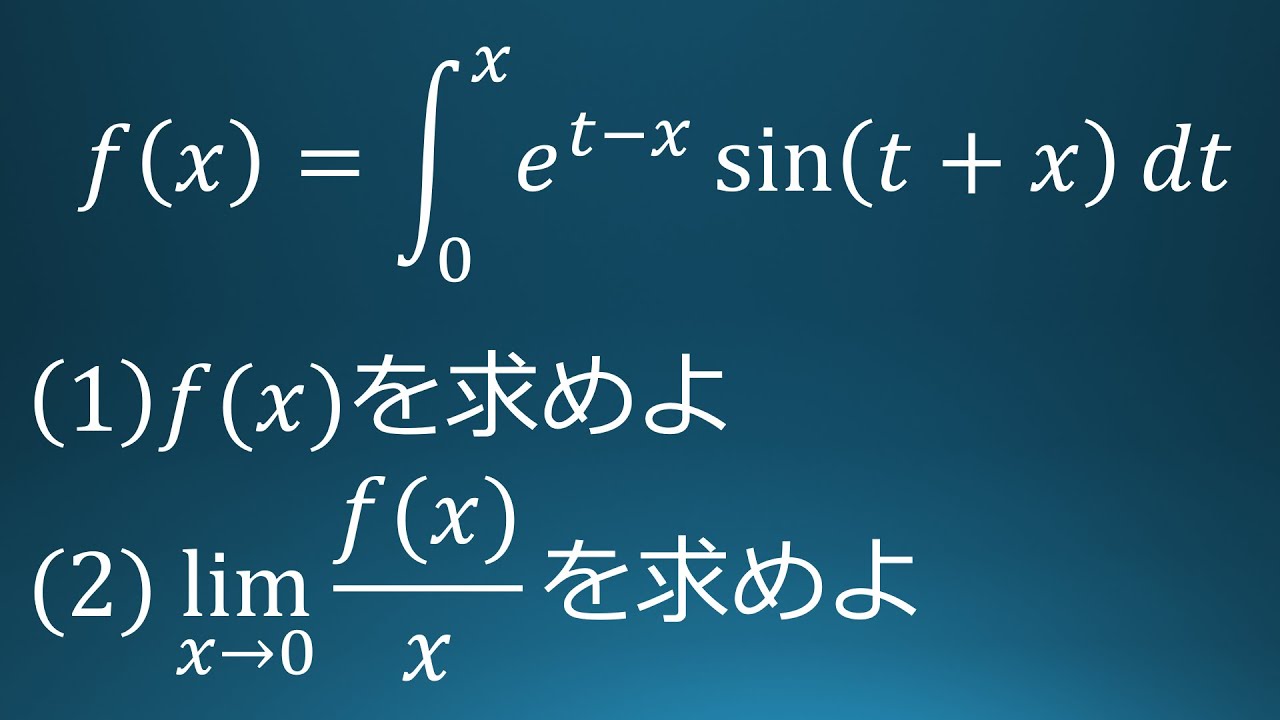
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
この動画を見る
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
数学「大学入試良問集」【16−2 複素数平面と三角形の形との関係】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
複素数平面上に三角形$ABC$があり、その頂点$A,B,C$を表す複素数をそれぞれ$z_1,z_2,z_3$とする。
複素数$\omega$に対して、$z_1=\omega z_3,z_2=\omega z_1,z_3=\omega z_2$が成り立つとき、次の各問いに答えよ。
(1)$1+\omega+\omega^2$の値を求めよ。
(2)三角形$ABC$はどんな形の三角形か。
(3)$z=z_1+2z_2+3z_3$の表す点を$D$とすると、三角形$OBD$はどんな形の三角形か。ただし、$O$は原点である。
この動画を見る
複素数平面上に三角形$ABC$があり、その頂点$A,B,C$を表す複素数をそれぞれ$z_1,z_2,z_3$とする。
複素数$\omega$に対して、$z_1=\omega z_3,z_2=\omega z_1,z_3=\omega z_2$が成り立つとき、次の各問いに答えよ。
(1)$1+\omega+\omega^2$の値を求めよ。
(2)三角形$ABC$はどんな形の三角形か。
(3)$z=z_1+2z_2+3z_3$の表す点を$D$とすると、三角形$OBD$はどんな形の三角形か。ただし、$O$は原点である。
【問題の詳細は概要欄,誘導あり】大学入試問題#22 千葉大学(2020) 数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a_1=3,a_2=2$
$n \geqq 2$のとき
$a_{n+1}=a_n^2+a_n-1$
(1)
$n \geqq 2$のとき
$a_{n+1}=(a_1・a_2・・・a_n)-1$を示せ
(2)
$\displaystyle \sum_{i=1}^n(a_1)^2=a_1a_2・・・a_n+100$をみたす自然数$n$を求めよ。
出典:2020年千葉大学 入試問題
この動画を見る
$a_1=3,a_2=2$
$n \geqq 2$のとき
$a_{n+1}=a_n^2+a_n-1$
(1)
$n \geqq 2$のとき
$a_{n+1}=(a_1・a_2・・・a_n)-1$を示せ
(2)
$\displaystyle \sum_{i=1}^n(a_1)^2=a_1a_2・・・a_n+100$をみたす自然数$n$を求めよ。
出典:2020年千葉大学 入試問題
大学入試問題#21 千葉大学(2020) tanの定積分
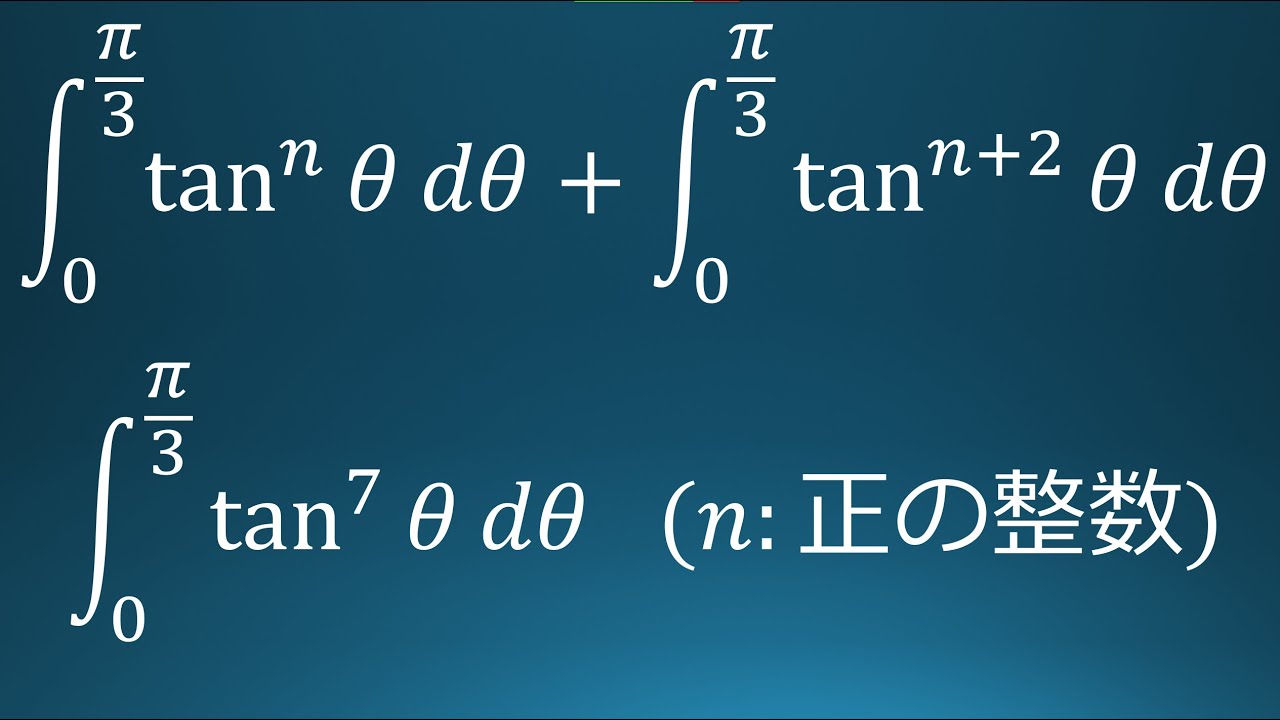
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
(1)
$\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^n\theta\ d\theta+\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^{n+2}\theta\ d\theta$を$n$の式で表せ
(2)
$\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^7\theta\ d\ \theta$を求めよ。
出典:2020年千葉大学 入試問題
この動画を見る
(1)
$\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^n\theta\ d\theta+\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^{n+2}\theta\ d\theta$を$n$の式で表せ
(2)
$\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^7\theta\ d\ \theta$を求めよ。
出典:2020年千葉大学 入試問題
数学「大学入試良問集」【7−1 二次関数の最大最小】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a$を正の実数とする。
2次関数$f(x)=ax^2-2(a+1)x+1$に対して、次の問いに答えよ。
(1)関数$y=f(x)$のグラフの頂点の座標を求めよ。
(2)$0 \leqq x \leqq 2$の範囲で$y=f(x)$の最大値と最小値を求めよ。
この動画を見る
$a$を正の実数とする。
2次関数$f(x)=ax^2-2(a+1)x+1$に対して、次の問いに答えよ。
(1)関数$y=f(x)$のグラフの頂点の座標を求めよ。
(2)$0 \leqq x \leqq 2$の範囲で$y=f(x)$の最大値と最小値を求めよ。
数学「大学入試良問集」【6−6 外接球と四面体】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
(1)$\angle BAC$を求めよ。
(2)$\triangle ABC$の外接円の半径を求めよ。
(3)4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
この動画を見る
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
(1)$\angle BAC$を求めよ。
(2)$\triangle ABC$の外接円の半径を求めよ。
(3)4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
【理数個別の過去問解説】2007年度千葉大学 数学 第2問解説

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは奇数とする。このとき、次のことを証明せよ。
(1)n²-1は8の倍数である。
(2)n⁵-nは3の倍数である。
(3)n⁵-nは120の倍数である。
千葉大学(文理共通)2007年第2問より
この動画を見る
nは奇数とする。このとき、次のことを証明せよ。
(1)n²-1は8の倍数である。
(2)n⁵-nは3の倍数である。
(3)n⁵-nは120の倍数である。
千葉大学(文理共通)2007年第2問より
千葉大 三次関数と円 東大数学科卒の杉山さん

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#円と方程式#指数関数#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
曲線$y=x^3-x$と円$(x-a^2)+(y-a)^2=2a^2$の共有点が2つ
共有点の$x$座標は?
$(a \gt 0)$
出典:千葉大学 過去問
この動画を見る
曲線$y=x^3-x$と円$(x-a^2)+(y-a)^2=2a^2$の共有点が2つ
共有点の$x$座標は?
$(a \gt 0)$
出典:千葉大学 過去問
千葉大 漸化式 良問再投稿

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n=\displaystyle \frac{(1+\sqrt{ 3 })^n+(1-\sqrt{ 3 })^n}{4}(n \geqq 2)$
以下を求めよ
$a_n$は整数
$a_n$は3で割ると余りが2
出典:2013年千葉大学 過去問
この動画を見る
$a_n=\displaystyle \frac{(1+\sqrt{ 3 })^n+(1-\sqrt{ 3 })^n}{4}(n \geqq 2)$
以下を求めよ
$a_n$は整数
$a_n$は3で割ると余りが2
出典:2013年千葉大学 過去問
千葉大 素数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b$は2以上の自然数
(1)
$a^b-1$が素数なら$a=2,b$は素数。示せ
(2)
$a^b+1$が素数なら$b=2^c(c$は自然数$)$示せ
出典:2007年千葉大学 過去問
この動画を見る
$a,b$は2以上の自然数
(1)
$a^b-1$が素数なら$a=2,b$は素数。示せ
(2)
$a^b+1$が素数なら$b=2^c(c$は自然数$)$示せ
出典:2007年千葉大学 過去問
千葉大 複素数 極形式 7乗根

単元:
#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#千葉大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\cos \displaystyle \frac{2}{7}\pi+i \sin \displaystyle \frac{2}{7}\pi$
(1)
$\alpha+\alpha^2+\alpha^3+\alpha^4+\alpha^5+\alpha^6$
(2)
$(1-\alpha)(1-\alpha^2)(1-\alpha^3)(1-\alpha^4)$
$(1-\alpha^5)(1-\alpha^6)$
(1)(2)それぞれ値を求めよ
出典:千葉大学 過去問
この動画を見る
$\alpha=\cos \displaystyle \frac{2}{7}\pi+i \sin \displaystyle \frac{2}{7}\pi$
(1)
$\alpha+\alpha^2+\alpha^3+\alpha^4+\alpha^5+\alpha^6$
(2)
$(1-\alpha)(1-\alpha^2)(1-\alpha^3)(1-\alpha^4)$
$(1-\alpha^5)(1-\alpha^6)$
(1)(2)それぞれ値を求めよ
出典:千葉大学 過去問
千葉大(医)整数問題 良問再投稿

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①
$3^n=k^3+1$
②
$3^n=k^2-40$
$k,n$自然数
出典:千葉大学大学院医学研究院・医学部 過去問
この動画を見る
①
$3^n=k^3+1$
②
$3^n=k^2-40$
$k,n$自然数
出典:千葉大学大学院医学研究院・医学部 過去問
千葉大 放物線と法線

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$C:y=\displaystyle \frac{1}{2}x^2$
点$(a,b)$を通る$C$の法線が3本引ける$a,b$の必要十分条件は?
出典:2010年千葉大学 過去問
この動画を見る
$C:y=\displaystyle \frac{1}{2}x^2$
点$(a,b)$を通る$C$の法線が3本引ける$a,b$の必要十分条件は?
出典:2010年千葉大学 過去問
千葉大 整式
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
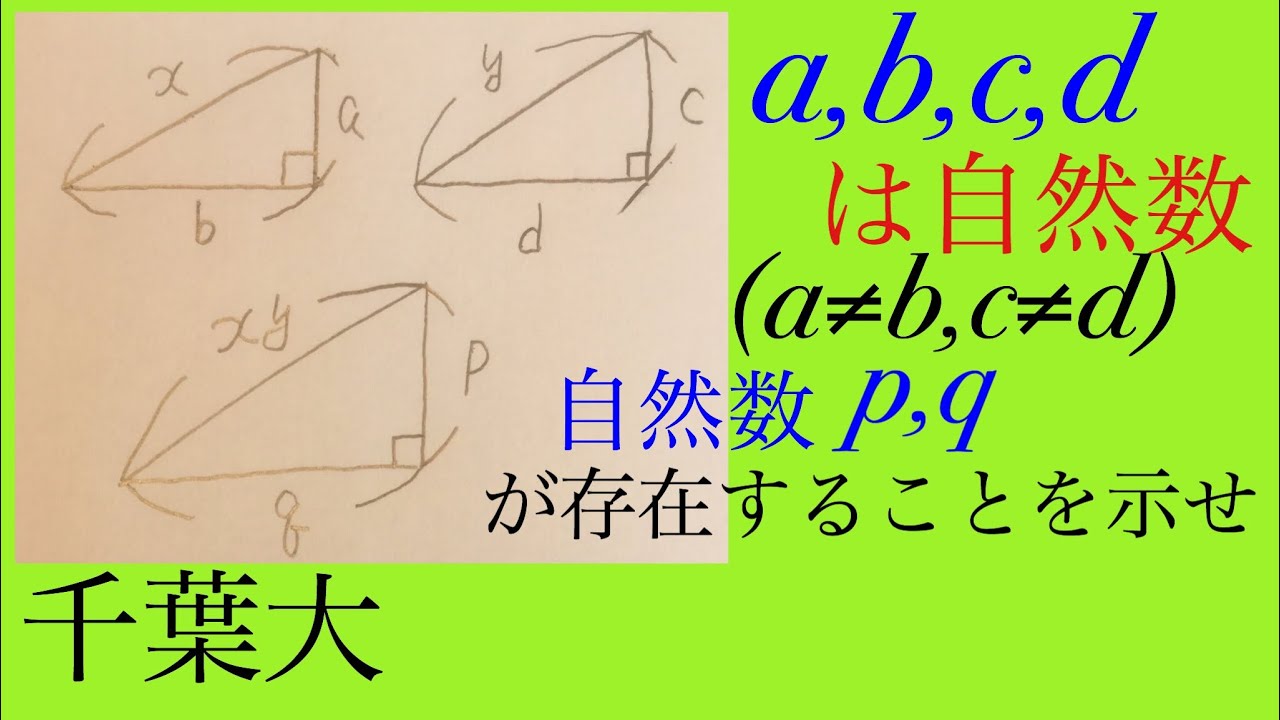
$a,b,c,d$は自然数
$a \neq b,c \neq d$
自然数$p,q$が存在することを示せ
出典:2004年千葉大学 過去問
この動画を見る
$a,b,c,d$は自然数
$a \neq b,c \neq d$
自然数$p,q$が存在することを示せ
出典:2004年千葉大学 過去問
千葉大 漸化式 証明

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学的帰納法#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_{n}\displaystyle \frac{(1+\sqrt{ 3 })^n+(1-\sqrt{ 3 })^n}{4}$
$n \geqq 2$の自然数
(1)
$a_{n}$は整数
(2)
$a_{n}$を3で割ると余りは2である
出典:2013年千葉大学 過去問
この動画を見る
$a_{n}\displaystyle \frac{(1+\sqrt{ 3 })^n+(1-\sqrt{ 3 })^n}{4}$
$n \geqq 2$の自然数
(1)
$a_{n}$は整数
(2)
$a_{n}$を3で割ると余りは2である
出典:2013年千葉大学 過去問
千葉大 整数問題 高校数学 Mathematics Japanese university entrance exam

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
下記証明せよ
(1)
$2x^2-y^2=9$を満たす整数$x,y$は3の倍数である
(2)
$21x^2-10y^2=9$を満たす整数$x,y$は存在しない
出典:千葉大学 過去問
この動画を見る
下記証明せよ
(1)
$2x^2-y^2=9$を満たす整数$x,y$は3の倍数である
(2)
$21x^2-10y^2=9$を満たす整数$x,y$は存在しない
出典:千葉大学 過去問
千葉大 二重絶対値記号のついた二次方程式の解の個数 Mathematics Japanese university entrance exam

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
千葉大学過去問題
$|x^2-6x-|x-6||+x=a$
実数解の個数(a実数)
この動画を見る
千葉大学過去問題
$|x^2-6x-|x-6||+x=a$
実数解の個数(a実数)
千葉大 漸化式 高校数学 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
90千葉大学過去問題
$a_1=1$
$3(a_1+a_2+\cdots +a_n)=(n+2)a_n$
(1)一般項$a_n$を求めよ。
(2)$\displaystyle\sum_{k=1}^n \frac{1}{a_k}$
この動画を見る
90千葉大学過去問題
$a_1=1$
$3(a_1+a_2+\cdots +a_n)=(n+2)a_n$
(1)一般項$a_n$を求めよ。
(2)$\displaystyle\sum_{k=1}^n \frac{1}{a_k}$
千葉大(医)訂正版 整数問題 Mathematics Japanese university entrance exam

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2013千葉大学過去問題
$m^4+14m^2$が$2m+1$の整数倍となるような整数mを全て
この動画を見る
2013千葉大学過去問題
$m^4+14m^2$が$2m+1$の整数倍となるような整数mを全て
千葉大(医)訂正版をご覧ください。別解をコメントしてくださった方がいるので、公開はします。Mathematics Japanese university entrance exam

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2013千葉大学過去問題
$m^4+14m^2$が$2m+1$の整数倍となるような整数mを全て求めよ.
この動画を見る
2013千葉大学過去問題
$m^4+14m^2$が$2m+1$の整数倍となるような整数mを全て求めよ.
千葉大 整数 Mathematics Japanese university entrance exam

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
千葉大学過去問題
$8n^3+40n$が$2n+1$で割り切れるような自然数nをすべて求めよ。
この動画を見る
千葉大学過去問題
$8n^3+40n$が$2n+1$で割り切れるような自然数nをすべて求めよ。
