 早稲田大学
早稲田大学
 早稲田大学
早稲田大学
早稲田の簡単すぎる問題!満点必須です【数学 入試問題】【早稲田大学】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$x$が$\dfrac{1}{3}≦x≦9$の範囲を動くとき,関数 $f(x)=(\log_\frac{1}{3}9x)(log_\frac{1}{3}\dfrac{x}{3})$の最大値と最小値を求めよ。
早稲田大過去問
この動画を見る
$x$が$\dfrac{1}{3}≦x≦9$の範囲を動くとき,関数 $f(x)=(\log_\frac{1}{3}9x)(log_\frac{1}{3}\dfrac{x}{3})$の最大値と最小値を求めよ。
早稲田大過去問
微分でもいいけど「あれ」を使えば一瞬です【数学 入試問題】【早稲田大学】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$x>0$のとき、$3x+\dfrac{1}{x^3}$の最小値とそのときの$x$の値を求めよ。
早稲田大過去問
この動画を見る
$x>0$のとき、$3x+\dfrac{1}{x^3}$の最小値とそのときの$x$の値を求めよ。
早稲田大過去問
早稲田(教育)見た目は数2か数3 中身は中学入試
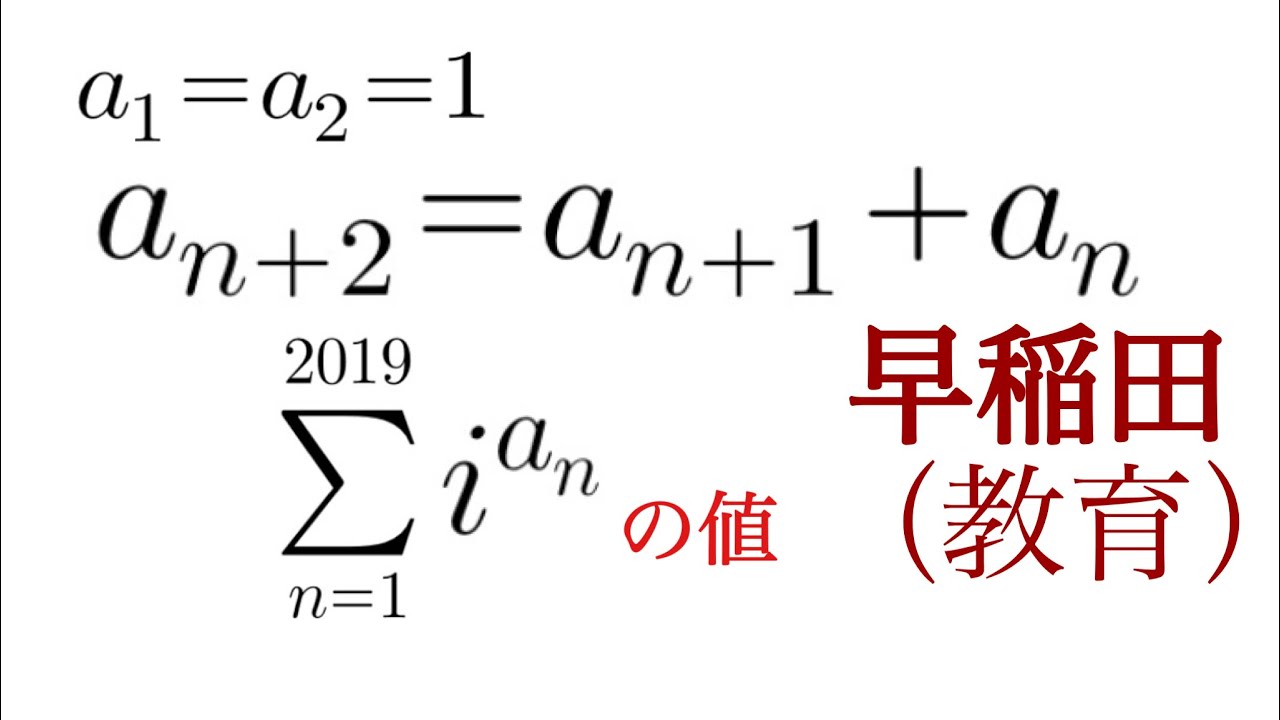
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#数列#早稲田大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=a_2=1,a_{n+2}=a_{n+1}+a_n,\displaystyle \sum_{n=1}^{2019} ia_n,$
$i$は虚数単位である.これを解け.
早稲田大(教育)過去問
この動画を見る
$ a_1=a_2=1,a_{n+2}=a_{n+1}+a_n,\displaystyle \sum_{n=1}^{2019} ia_n,$
$i$は虚数単位である.これを解け.
早稲田大(教育)過去問
大学入試問題#189 早稲田大学(2005) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{2}\displaystyle \frac{3}{1-x+x^2}\ dx$を計算せよ。
出典:2005年早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{2}\displaystyle \frac{3}{1-x+x^2}\ dx$を計算せよ。
出典:2005年早稲田大学 入試問題
早稲田(教)基本問題

単元:
#約数・倍数を利用する問題#大学入試過去問(数学)#早稲田大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1~15n$の整数のうち3の倍数でも5の倍数でもない数の総和を求めよ.
早稲田(教)過去問
この動画を見る
$1~15n$の整数のうち3の倍数でも5の倍数でもない数の総和を求めよ.
早稲田(教)過去問
大学入試問題#184 早稲田大学 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}dx$を計算せよ
出典:早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}dx$を計算せよ
出典:早稲田大学 入試問題
一文字削除からの判別式【2014年早稲田大学】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
実数$a,b,c$が
$a+b+c=8,a^2+b^2+c^2=32$
を満たす時、実数$c$の最大値を求めよ。
2014早稲田大過去問
この動画を見る
実数$a,b,c$が
$a+b+c=8,a^2+b^2+c^2=32$
を満たす時、実数$c$の最大値を求めよ。
2014早稲田大過去問
対称式の良問【2008年早稲田大学】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
実数$x$が$x^3+\dfrac{1}{x^3}=52$を満たすとき、$x^4+\dfrac{1}{x^4}$の値を求めよ。
2008早稲田大過去問
この動画を見る
実数$x$が$x^3+\dfrac{1}{x^3}=52$を満たすとき、$x^4+\dfrac{1}{x^4}$の値を求めよ。
2008早稲田大過去問
2022早稲田大(社)整式の剰余

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整式P(x)をx-1で割ると1あまり,$ (x+1)^2 $で割ると3x+2あまる.
P(x)を次の式で割ったあまりは?
(1)$ x+1$ (2)$(x+1)(x-1)$ (3)$(x-1)(x+1)^2$
2022早稲田大過去問
この動画を見る
整式P(x)をx-1で割ると1あまり,$ (x+1)^2 $で割ると3x+2あまる.
P(x)を次の式で割ったあまりは?
(1)$ x+1$ (2)$(x+1)(x-1)$ (3)$(x-1)(x+1)^2$
2022早稲田大過去問
大学入試問題#120 早稲田大学(2003) 対数の不等式
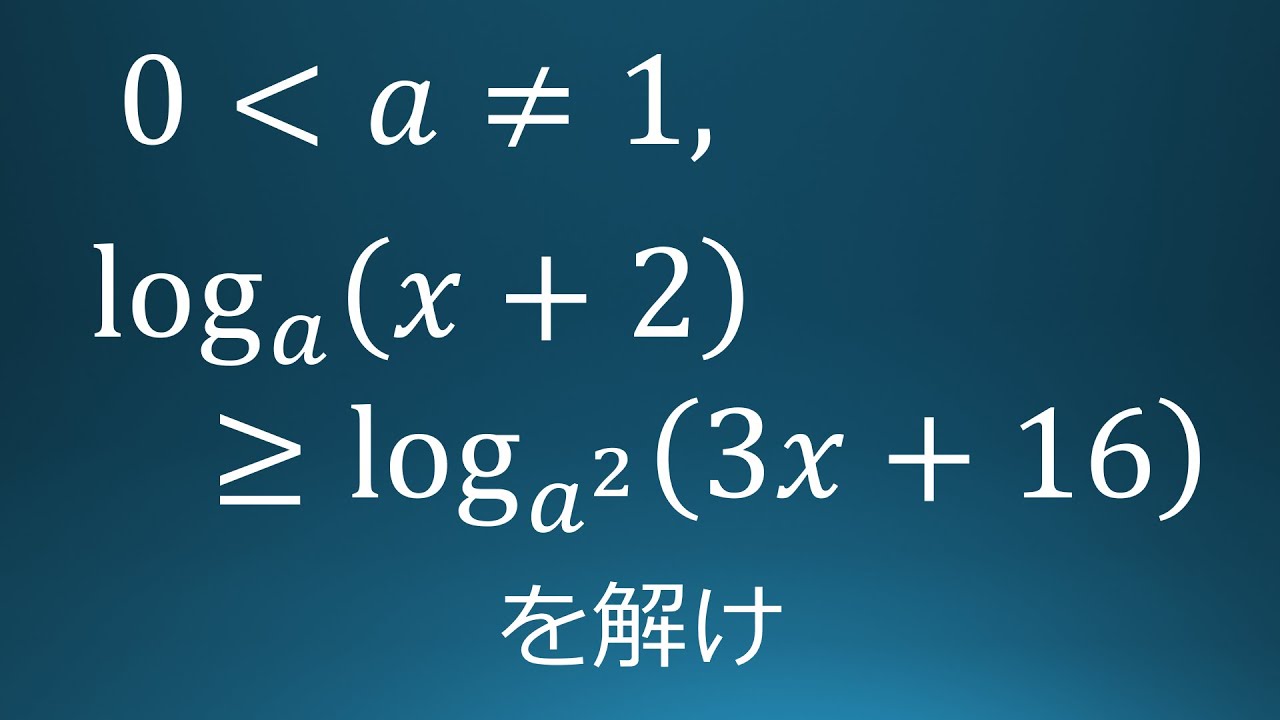
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0,\ a \neq 1$
$log\ a(x+2) \geqq log\ a^2(3x+16)$を解け
出典:2003年早稲田大学 入試問題
この動画を見る
$a \gt 0,\ a \neq 1$
$log\ a(x+2) \geqq log\ a^2(3x+16)$を解け
出典:2003年早稲田大学 入試問題
大学入試問題#111 早稲田大学(2021) 次数下げ
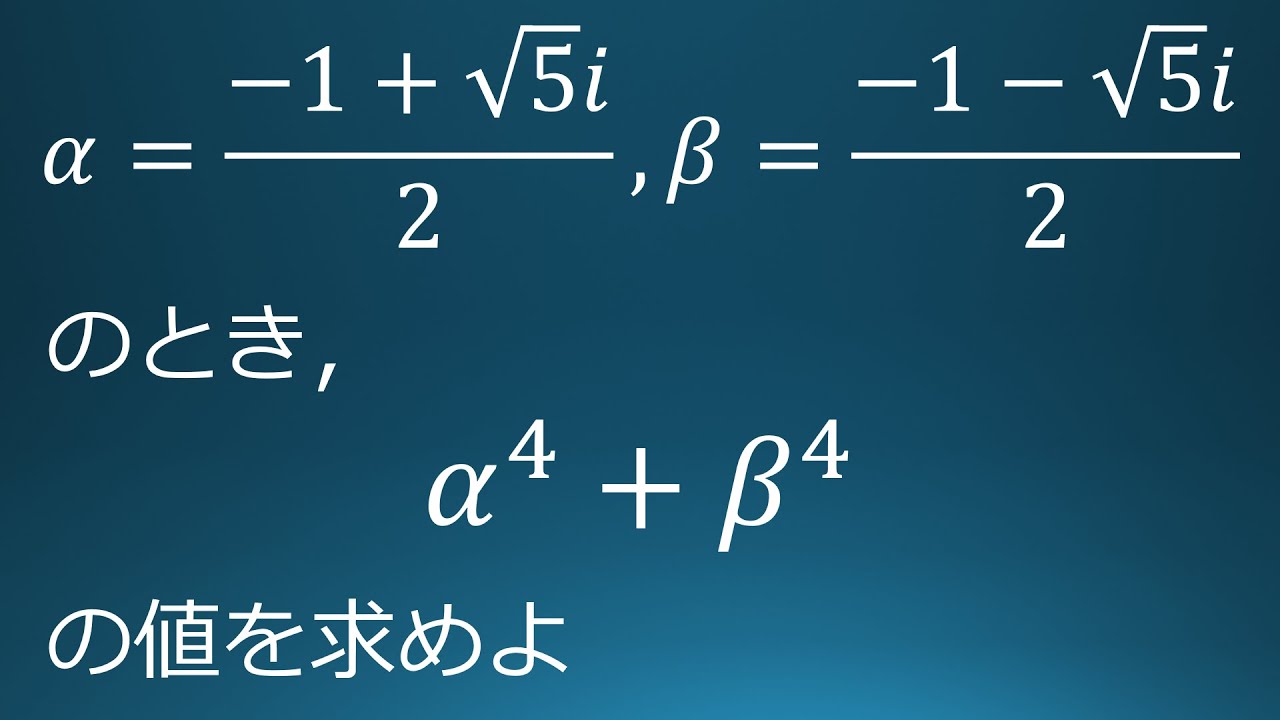
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\alpha=\displaystyle \frac{-1+\sqrt{ 5 }i}{2}$
$\beta=\displaystyle \frac{-1-\sqrt{ 5 }i}{2}$のとき
$\alpha^4+\beta^4$の値を求めよ。
出典:2021年早稲田大学 入試問題
この動画を見る
$\alpha=\displaystyle \frac{-1+\sqrt{ 5 }i}{2}$
$\beta=\displaystyle \frac{-1-\sqrt{ 5 }i}{2}$のとき
$\alpha^4+\beta^4$の値を求めよ。
出典:2021年早稲田大学 入試問題
大学入試問題#64 早稲田大学(1987) 置換積分
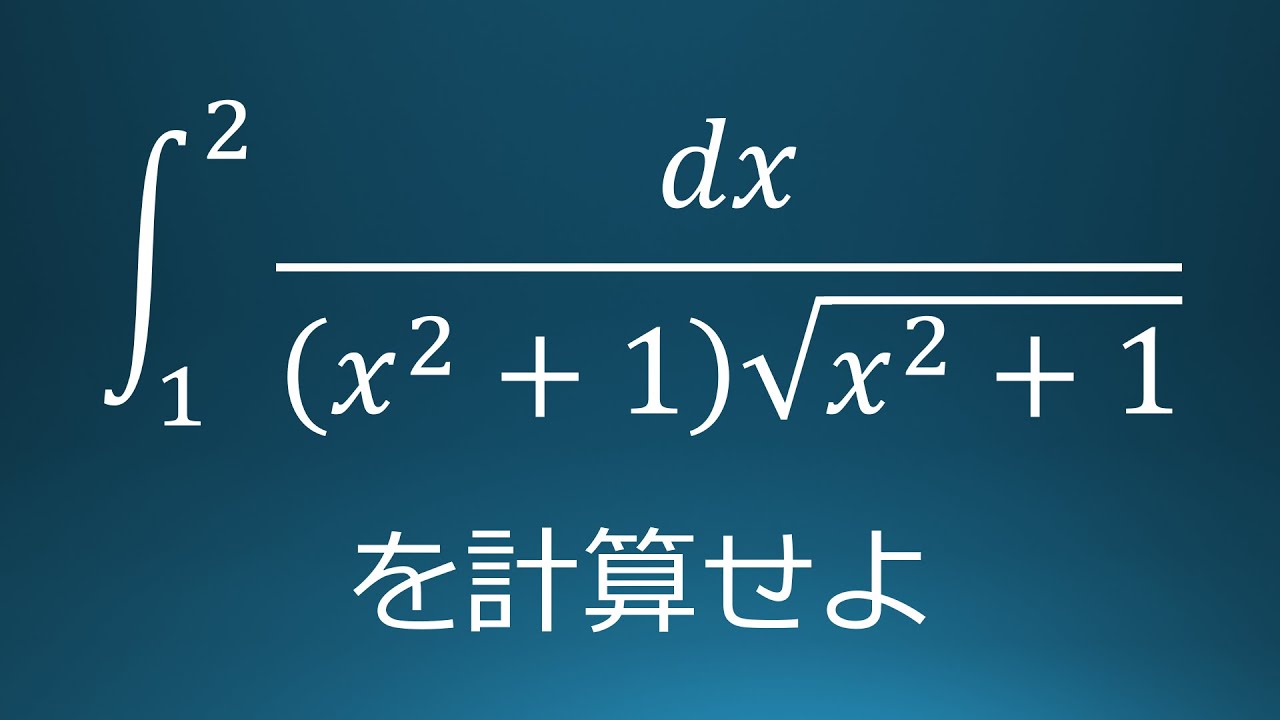
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2}\displaystyle \frac{dx}{(x^2+1)\sqrt{ x^2+1 }}$を計算せよ。
出典:1987年早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2}\displaystyle \frac{dx}{(x^2+1)\sqrt{ x^2+1 }}$を計算せよ。
出典:1987年早稲田大学 入試問題
大学入試問題#55 早稲田大学(2021) Σの計算
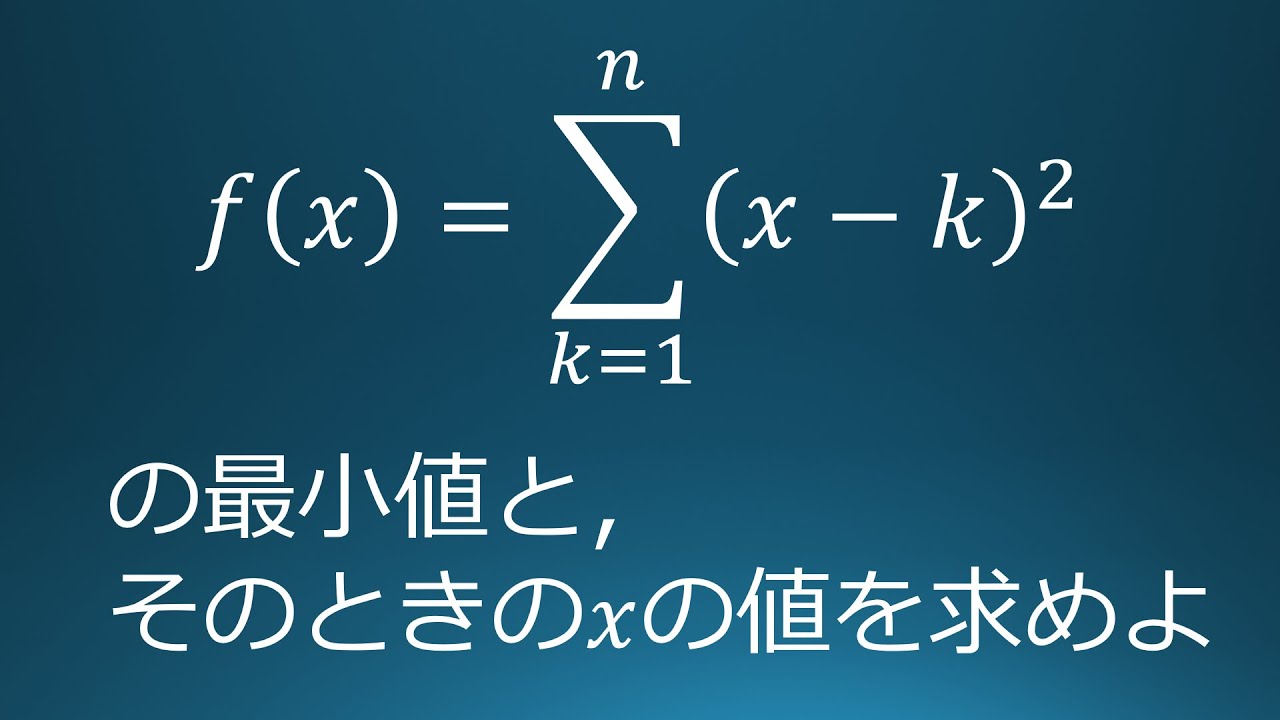
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \sum_{k=1}^n(x-k)^2$の最小値とそのときの$x$の値を$n$で表せ
出典:2021年早稲田大学 入試問題
この動画を見る
$f(x)=\displaystyle \sum_{k=1}^n(x-k)^2$の最小値とそのときの$x$の値を$n$で表せ
出典:2021年早稲田大学 入試問題
大学入試問題#54 早稲田大学(2021) 積分の応用

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$m,n:$正の整数
$f(x):n:x$次関数
$\displaystyle \int_{0}^{x}(x-t)^{m-1}f(t)dt=\{f(x)\}^m$を満たすとき$f(x)$を求めよ。
出典:2021年早稲田大学 入試問題
この動画を見る
$m,n:$正の整数
$f(x):n:x$次関数
$\displaystyle \int_{0}^{x}(x-t)^{m-1}f(t)dt=\{f(x)\}^m$を満たすとき$f(x)$を求めよ。
出典:2021年早稲田大学 入試問題
数学「大学入試良問集」【14−11空間ベクトルと正四面体】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
四面体$OABC$の辺$AB$を$4:5$に内分する点を$D$、辺$OC$を$2:1$に内分する点を$E$とし、線分$DE$の中点を$P$、直線$OP$が平面$ABC$と交わる点を$Q$とする。
次の各問いに答えよ。
(1)
$\overrightarrow{ OA }=\vec{ a },\ \overrightarrow{ OB }=\vec{ b },\ \overrightarrow{ OC }=\vec{ c }$とおくとき、$\overrightarrow{ OP }$を$\vec{ a },\ \vec{ b },\ \vec{ c }$で表せ。
また、$\overrightarrow{ OP }$と$\overrightarrow{ OQ }$の大きさの比$|\overrightarrow{ OP }|:|\overrightarrow{ OQ }|$を最も簡単な整数比で表せ。
(2)
$\triangle ABQ$と$\triangle ABC$の面積比$\triangle ABQ:\triangle ABC$を最も簡単な整数比で表せ。
この動画を見る
四面体$OABC$の辺$AB$を$4:5$に内分する点を$D$、辺$OC$を$2:1$に内分する点を$E$とし、線分$DE$の中点を$P$、直線$OP$が平面$ABC$と交わる点を$Q$とする。
次の各問いに答えよ。
(1)
$\overrightarrow{ OA }=\vec{ a },\ \overrightarrow{ OB }=\vec{ b },\ \overrightarrow{ OC }=\vec{ c }$とおくとき、$\overrightarrow{ OP }$を$\vec{ a },\ \vec{ b },\ \vec{ c }$で表せ。
また、$\overrightarrow{ OP }$と$\overrightarrow{ OQ }$の大きさの比$|\overrightarrow{ OP }|:|\overrightarrow{ OQ }|$を最も簡単な整数比で表せ。
(2)
$\triangle ABQ$と$\triangle ABC$の面積比$\triangle ABQ:\triangle ABC$を最も簡単な整数比で表せ。
大学入試問題#37 早稲田大学(2021) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a,b,c:$実数
$0 \leqq a \leqq b \leqq c$
$a+b+c=7$を満たすとき
$ab,bc,ca$の最大値を求めよ。
出典:2021年早稲田大学 入試問題
この動画を見る
$a,b,c:$実数
$0 \leqq a \leqq b \leqq c$
$a+b+c=7$を満たすとき
$ab,bc,ca$の最大値を求めよ。
出典:2021年早稲田大学 入試問題
数学「大学入試良問集」【14−1 平面ベクトルと一次独立の様々な解法】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\triangle OAB$を$3:2$に内部する点を$C$、辺$OB$を$3:4$に内分する点を$D$とする。
線分$AD$と線分$BC$との交点を$P$とする。
また、$\triangle OPA,\triangle PDB$の面積をそれぞれ$S_1,S_2$とする。
(1)$\overrightarrow{ OP }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
(2)$S_1:S_2$を求めよ。
この動画を見る
$\triangle OAB$を$3:2$に内部する点を$C$、辺$OB$を$3:4$に内分する点を$D$とする。
線分$AD$と線分$BC$との交点を$P$とする。
また、$\triangle OPA,\triangle PDB$の面積をそれぞれ$S_1,S_2$とする。
(1)$\overrightarrow{ OP }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
(2)$S_1:S_2$を求めよ。
練習問題42 早稲田大学 定積分 数学検定1級 教員採用試験
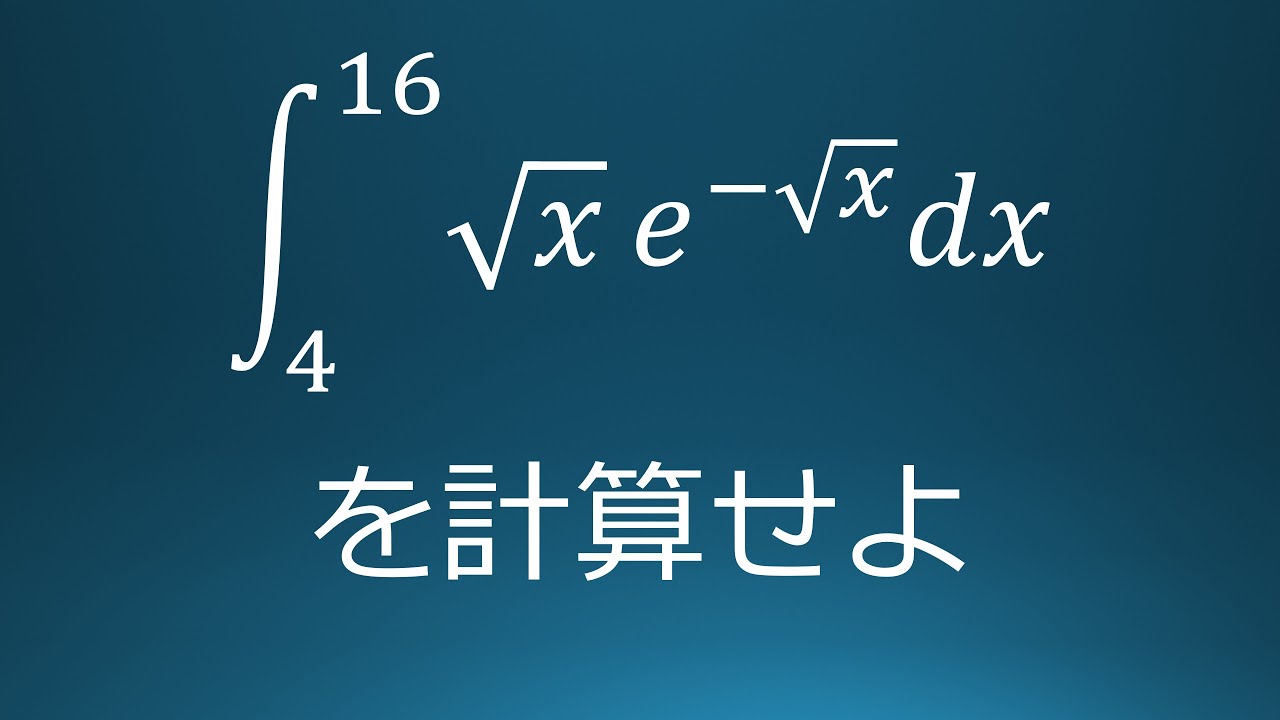
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#その他#早稲田大学#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}\ dx$
出典:早稲田大学 教員採用試験
この動画を見る
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}\ dx$
出典:早稲田大学 教員採用試験
福田の数学〜慶應義塾大学2021年医学部第1問(2)〜回転体の体積と極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $(2)0 \lt \alpha \lt 1,m \gt 0$とする。$曲線y=x^{\alpha}-mx(x \geqq 0)$と$x軸$で囲まれた図形を$x軸$の周りに1回転させてできる回転体の体積を$V$とする。$m$を固定して$a \to +0$とするときの$V$の極限値を$m$の式で表すと、$\lim_{a \to +0}V=\boxed{\ \ (え)\ \ }$となる。
また、$\alpha$を固定して$m \to \infty$とするとき$m^3V$が$0$でない数に収束するならば
$\alpha=\boxed{\ \ (お)\ \ }$である。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{1}}$ $(2)0 \lt \alpha \lt 1,m \gt 0$とする。$曲線y=x^{\alpha}-mx(x \geqq 0)$と$x軸$で囲まれた図形を$x軸$の周りに1回転させてできる回転体の体積を$V$とする。$m$を固定して$a \to +0$とするときの$V$の極限値を$m$の式で表すと、$\lim_{a \to +0}V=\boxed{\ \ (え)\ \ }$となる。
また、$\alpha$を固定して$m \to \infty$とするとき$m^3V$が$0$でない数に収束するならば
$\alpha=\boxed{\ \ (お)\ \ }$である。
2021慶應義塾大学医学部過去問
福田の数学〜早稲田大学2021年人間科学部第7問〜双曲線と図形問題

単元:
#数Ⅰ#大学入試過去問(数学)#平面上の曲線#図形と計量#2次曲線#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年人間科学部第6問〜回転で定義された点列の極限

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{6}}$ 点$M_1(0,0)$を中心に$点(1,0)$を、時計の針の回転と逆の向きを正として、$\theta$だけ回転させた点を$P_1$とする。次に$線分M_1P_1$の$中点M_2$とし、この$M_2$を中心に$点P_1$を$\theta$だけ回転させた点を$P_2$とする。同様に自然数$n$に対して、$線分M_nP_n$の$中点M_{n+1}$を中心に$点P_n$を$\theta$だけ回転させた点を$P_{n+1}$とする。$P_n$の座標を$(x_n,y_n)$とする。
$(1)\theta=\frac{\pi}{4}$のとき、$x_2=\frac{\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }},$$ y_2=\frac{\boxed{\ \ ツ\ \ }+\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
$(2)\theta=\frac{\pi}{3}$のとき、$\lim_{n \to \infty}x_n=\boxed{\ \ ナ\ \ },$ $\lim_{n \to \infty}y_n=\frac{\sqrt{\boxed{\ \ ニ\ \ }}}{\boxed{\ \ ヌ\ \ }}$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{6}}$ 点$M_1(0,0)$を中心に$点(1,0)$を、時計の針の回転と逆の向きを正として、$\theta$だけ回転させた点を$P_1$とする。次に$線分M_1P_1$の$中点M_2$とし、この$M_2$を中心に$点P_1$を$\theta$だけ回転させた点を$P_2$とする。同様に自然数$n$に対して、$線分M_nP_n$の$中点M_{n+1}$を中心に$点P_n$を$\theta$だけ回転させた点を$P_{n+1}$とする。$P_n$の座標を$(x_n,y_n)$とする。
$(1)\theta=\frac{\pi}{4}$のとき、$x_2=\frac{\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }},$$ y_2=\frac{\boxed{\ \ ツ\ \ }+\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
$(2)\theta=\frac{\pi}{3}$のとき、$\lim_{n \to \infty}x_n=\boxed{\ \ ナ\ \ },$ $\lim_{n \to \infty}y_n=\frac{\sqrt{\boxed{\ \ ニ\ \ }}}{\boxed{\ \ ヌ\ \ }}$である。
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年人間科学部第5問〜漸化式の作成と値の評価

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$ 半径$r_1=2$の円$O_1$に接する平行でない$2$つの直線がある。接点を$A,B$とし、$2$つの直線の交点を$P$とし、$\angle APB=\frac{\pi}{3}$とする。$O_1$より半径が小さく、$O_1$の中心を通り、直線$AP$と直線$BP$に接する円を$O_2$とする。同様に自然数$n$に対して、$O_n$より半径が小さく、$O_n$の中心を通り、直線$AP$と直線$BP$に接する円を$O_{n+1}$とする。$O_n$の半径を$r_n$とするとき、$\frac{r_n}{r_{n+1}}=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$ となる。次に、$n$個の円$O_1,O_2,\ldots,O_n$の面積の和を$S_n$とするとき、$S_{10}$の整数部分は$\boxed{\ \ ヒ\ \ }$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{5}}$ 半径$r_1=2$の円$O_1$に接する平行でない$2$つの直線がある。接点を$A,B$とし、$2$つの直線の交点を$P$とし、$\angle APB=\frac{\pi}{3}$とする。$O_1$より半径が小さく、$O_1$の中心を通り、直線$AP$と直線$BP$に接する円を$O_2$とする。同様に自然数$n$に対して、$O_n$より半径が小さく、$O_n$の中心を通り、直線$AP$と直線$BP$に接する円を$O_{n+1}$とする。$O_n$の半径を$r_n$とするとき、$\frac{r_n}{r_{n+1}}=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$ となる。次に、$n$個の円$O_1,O_2,\ldots,O_n$の面積の和を$S_n$とするとき、$S_{10}$の整数部分は$\boxed{\ \ ヒ\ \ }$である。
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年人間科学部第4問〜領域における最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$
不等式$(x-6)^2+(y-4)^2 \leqq 4$の表す領域を点$\textrm{P}(x,y)$が動くものとする。
このとき、$x^2+y^2$の最大値は$\boxed{\ \ タ\ \ }+\boxed{\ \ チ\ \ }\sqrt{\boxed{\ \ ツ\ \ }}$、$\dfrac{y}{x}$の最小値は$\dfrac{\boxed{\ \ テ\ \ }-\sqrt{\boxed{\ \ ト\ \ }}}{\boxed{\ \ ナ\ \ }}$、$x+y$の最大値は$\boxed{\ \ ニ\ \ }+\boxed{\ \ ヌ\ \ }\sqrt{\boxed{\ \ ネ\ \ }}$となる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{4}}$
不等式$(x-6)^2+(y-4)^2 \leqq 4$の表す領域を点$\textrm{P}(x,y)$が動くものとする。
このとき、$x^2+y^2$の最大値は$\boxed{\ \ タ\ \ }+\boxed{\ \ チ\ \ }\sqrt{\boxed{\ \ ツ\ \ }}$、$\dfrac{y}{x}$の最小値は$\dfrac{\boxed{\ \ テ\ \ }-\sqrt{\boxed{\ \ ト\ \ }}}{\boxed{\ \ ナ\ \ }}$、$x+y$の最大値は$\boxed{\ \ ニ\ \ }+\boxed{\ \ ヌ\ \ }\sqrt{\boxed{\ \ ネ\ \ }}$となる。
2021早稲田大学人間科学部過去問
田の数学〜早稲田大学2021年人間科学部第3問〜格子点の個数

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$
自然数$n$について、連立不等式
$\left\{\begin{array}{1}
x \geqq 0\\
\displaystyle\frac{1}{4}x+\frac{1}{5}|y| \leqq n\\
\end{array}\right.$
を満たす整数の組$(x, y)$の個数は、$n=1$のときは$\boxed{\ \ シ\ \ }$であり、$n$の式で表すと$\boxed{\ \ ス\ \ }n^2+\boxed{\ \ セ\ \ }n+\boxed{\ \ ソ\ \ }$となる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{3}}$
自然数$n$について、連立不等式
$\left\{\begin{array}{1}
x \geqq 0\\
\displaystyle\frac{1}{4}x+\frac{1}{5}|y| \leqq n\\
\end{array}\right.$
を満たす整数の組$(x, y)$の個数は、$n=1$のときは$\boxed{\ \ シ\ \ }$であり、$n$の式で表すと$\boxed{\ \ ス\ \ }n^2+\boxed{\ \ セ\ \ }n+\boxed{\ \ ソ\ \ }$となる。
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年人間科学部第2問(3)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
この動画を見る
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
福田の数学〜早稲田大学2021年人間科学部第2問(2)〜3辺の長さから三角形の面積を求める

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(2)3辺の長さがそれぞれ$5,16,19$の三角形の面積は$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{2}}$
(2)3辺の長さがそれぞれ$5,16,19$の三角形の面積は$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$である。
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年人間科学部第2問(1)〜指数対数不等式の表す領域の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#軌跡と領域#指数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(1)次の連立不等式の表す領域の面積は$\dfrac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}$ である。
$\left\{\begin{array}{1}
\displaystyle\log_4y+\log_{\frac{1}{4}}(x-2)+\log_4\frac{1}{8-x} \geqq -1\\
2^{y+x^2+11} \leqq 1024^{x-1}\\
\end{array}\right.$
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{2}}$
(1)次の連立不等式の表す領域の面積は$\dfrac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}$ である。
$\left\{\begin{array}{1}
\displaystyle\log_4y+\log_{\frac{1}{4}}(x-2)+\log_4\frac{1}{8-x} \geqq -1\\
2^{y+x^2+11} \leqq 1024^{x-1}\\
\end{array}\right.$
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年人間科学部第1問〜異なるペアになる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(1)8人のメンバーで、2人組(ペア)を4組作る方法は$n$通りある。$n$を$100$で割った商は$\boxed{\ \ ア\ \ }$で、余りは$\boxed{\ \ イ\ \ }$である。
(2)8人のメンバーで、2人組(ペア)を4組作って、ある作業に取り組んだ後、同じ8人で次の作業に取り組むペアを作るために、くじ引きをした。このとき、8人全員がくじ引き前と異なるメンバーとペアになる確率は$\dfrac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$ である。
ただし、くじは公平でどの2人もペアになる確率は等しいものとする。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{1}}$
(1)8人のメンバーで、2人組(ペア)を4組作る方法は$n$通りある。$n$を$100$で割った商は$\boxed{\ \ ア\ \ }$で、余りは$\boxed{\ \ イ\ \ }$である。
(2)8人のメンバーで、2人組(ペア)を4組作って、ある作業に取り組んだ後、同じ8人で次の作業に取り組むペアを作るために、くじ引きをした。このとき、8人全員がくじ引き前と異なるメンバーとペアになる確率は$\dfrac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$ である。
ただし、くじは公平でどの2人もペアになる確率は等しいものとする。
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年商学部第3問〜正の約数の総和が奇数になる条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ 次の設問に答えよ。
(1)$225$の全ての正の約数の和を求めよ。
(2)$2021$以下の正の整数で、すべての正の約数の和が奇数であるものの個数を求めよ。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{3}}$ 次の設問に答えよ。
(1)$225$の全ての正の約数の和を求めよ。
(2)$2021$以下の正の整数で、すべての正の約数の和が奇数であるものの個数を求めよ。
2021早稲田大学商学部過去問
福田の数学〜早稲田大学2021年商学部第2問〜空間図形の共通部分

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
