大学入試過去問(数学)
大学入試過去問(数学)
福田の数学〜東京大学2018年理系第1問〜関数の増減と極限の計算
単元：
#大学入試過去問(数学)#関数と極限#微分とその応用#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=\dfrac{x}{\sin x}+\cos x (0 \lt x \lt \pi)$のぞうげんひょうを作り、$x→+0,x→\pi-0$のときの極限を調べよ。
2018東京大学理過去問
この動画を見る
$f(x)=\dfrac{x}{\sin x}+\cos x (0 \lt x \lt \pi)$のぞうげんひょうを作り、$x→+0,x→\pi-0$のときの極限を調べよ。
2018東京大学理過去問
大学入試問題#730「総和と間違えそう」 早稲田大学商学部(2011) 個数の処理
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$n$を正の整数とする。
$10^n$の正の約数すべての積の値を求めよ。
出典：2011年早稲田大学商学部 入試問題
この動画を見る
$n$を正の整数とする。
$10^n$の正の約数すべての積の値を求めよ。
出典：2011年早稲田大学商学部 入試問題
【高校数学】毎日積分58日目~47都道府県制覇への道~【②鹿児島】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x＞0$で定義された曲線
$C : y=(log x)^2$
を考える
(1)$a$を正の実数とする時、点$P(a,(log a)^2)$における曲線$C$の接線$L$の方程式を求めよ。
(2)$a＞1$のとき、接線$L$と$x$軸の交点の$x$座標が最大となる場合の$a$の値$a_0$を求めよ。
(3)$a$の値が(2)の$a_0$に等しいとき、直線$L$の$y≧0$の部分と曲線$C$と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる図形の体積を求めよ。
【鹿児島大学 2023】
この動画を見る
$x＞0$で定義された曲線
$C : y=(log x)^2$
を考える
(1)$a$を正の実数とする時、点$P(a,(log a)^2)$における曲線$C$の接線$L$の方程式を求めよ。
(2)$a＞1$のとき、接線$L$と$x$軸の交点の$x$座標が最大となる場合の$a$の値$a_0$を求めよ。
(3)$a$の値が(2)の$a_0$に等しいとき、直線$L$の$y≧0$の部分と曲線$C$と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる図形の体積を求めよ。
【鹿児島大学 2023】
大学入試問題#729「医学部なら落とせん」 関西医科大学(2021) 整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$x^2-|x|y+y^2=3$を満たす整数の組$(x,y)$をすべて求めよ。
出典：2021年関西医科大学 入試問題
この動画を見る
$x^2-|x|y+y^2=3$を満たす整数の組$(x,y)$をすべて求めよ。
出典：2021年関西医科大学 入試問題
【高校数学】毎日積分57日目~47都道府県制覇への道~【①沖縄】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$a$を実数とし、$f(x)=xe^{-|x|}, g(x)=ax$とおく。次の問いに答えよ。
問1 $f(x)$の増減を調べ、$y=f(x)$のグラフの概形をかけ。ただし$\displaystyle \lim_{x\to \infty}xe^{-x}=0$は証明なしに用いてよい。
問2 $0＜a＜1$のとき、曲線$y=f(x)$と直線$y=g(x)$で囲まれた2つの部分の面積の和を求めよ。
【琉球大学 2023】
この動画を見る
$a$を実数とし、$f(x)=xe^{-|x|}, g(x)=ax$とおく。次の問いに答えよ。
問1 $f(x)$の増減を調べ、$y=f(x)$のグラフの概形をかけ。ただし$\displaystyle \lim_{x\to \infty}xe^{-x}=0$は証明なしに用いてよい。
問2 $0＜a＜1$のとき、曲線$y=f(x)$と直線$y=g(x)$で囲まれた2つの部分の面積の和を求めよ。
【琉球大学 2023】
大学入試問題#728「たぶん良問」 早稲田大学商学部(2014) 積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
任意の実数$x$に対して、
$\displaystyle \int_{0}^{x} f(t) dt-3\displaystyle \int_{-x}^{0} f(t) dt=x^3$を満たす関数$f(x)$を求めよ
出典：2014年早稲田大学商学部 入試問題
この動画を見る
任意の実数$x$に対して、
$\displaystyle \int_{0}^{x} f(t) dt-3\displaystyle \int_{-x}^{0} f(t) dt=x^3$を満たす関数$f(x)$を求めよ
出典：2014年早稲田大学商学部 入試問題
整数問題 2024福岡大附属大濠
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
x-1が9の倍数であるとき$x^2$を3で割った余りは？
2024福岡大学附属大濠高等学校
この動画を見る
x-1が9の倍数であるとき$x^2$を3で割った余りは？
2024福岡大学附属大濠高等学校
大学入試問題#727 三重大学医学部etc (2023) 三角関数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
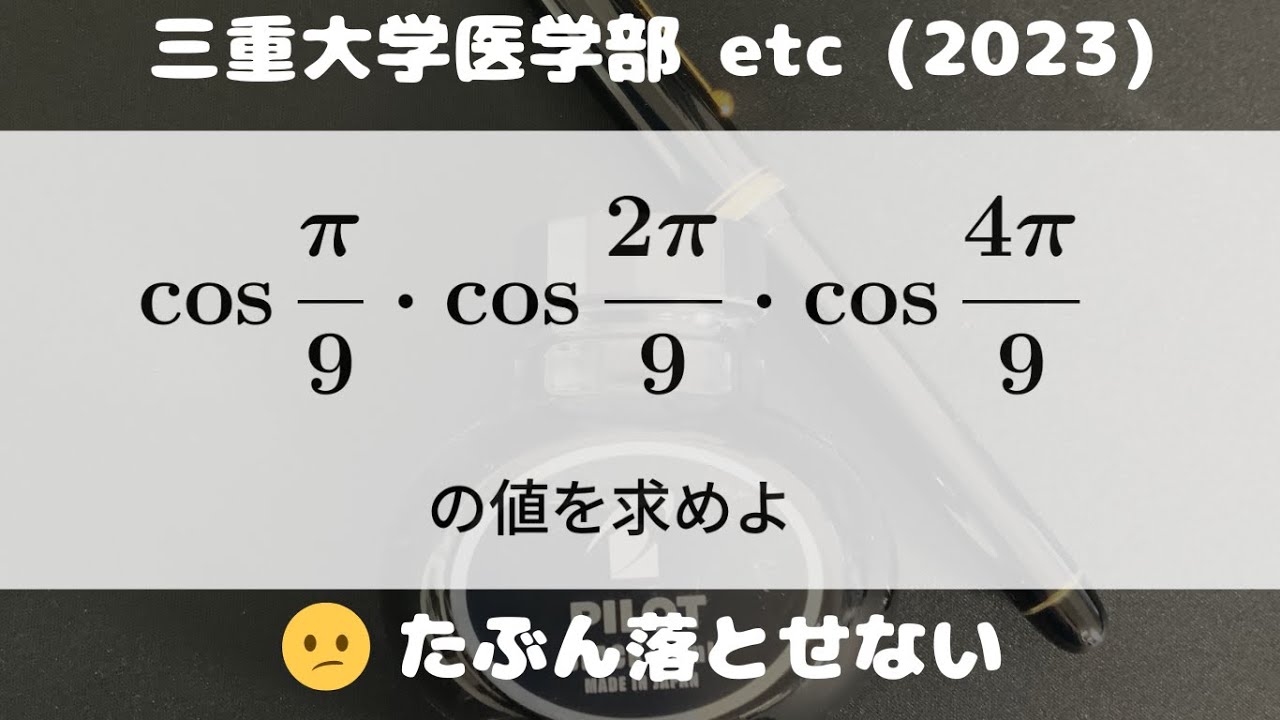
$\cos\displaystyle \frac{\pi}{9}・\cos\displaystyle \frac{2\pi}{9}・\cos\displaystyle \frac{4\pi}{9}$の値を求めよ
出典：2023年三重大学医学部 入試問題
この動画を見る
$\cos\displaystyle \frac{\pi}{9}・\cos\displaystyle \frac{2\pi}{9}・\cos\displaystyle \frac{4\pi}{9}$の値を求めよ
出典：2023年三重大学医学部 入試問題
大学受験過去問シリーズ！横浜国立大2019年（理系）第4問の解説 #数学 #過去問 #横浜国立大学
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
横浜国立大2019年（理系）第4問の解説していきます.
この動画を見る
横浜国立大2019年（理系）第4問の解説していきます.
大学入試問題#726「一橋レベルでこれは落とせん」 一橋大学(2021)積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典：2021年一橋大学後期 入試問題
この動画を見る
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典：2021年一橋大学後期 入試問題
関西大学 2011
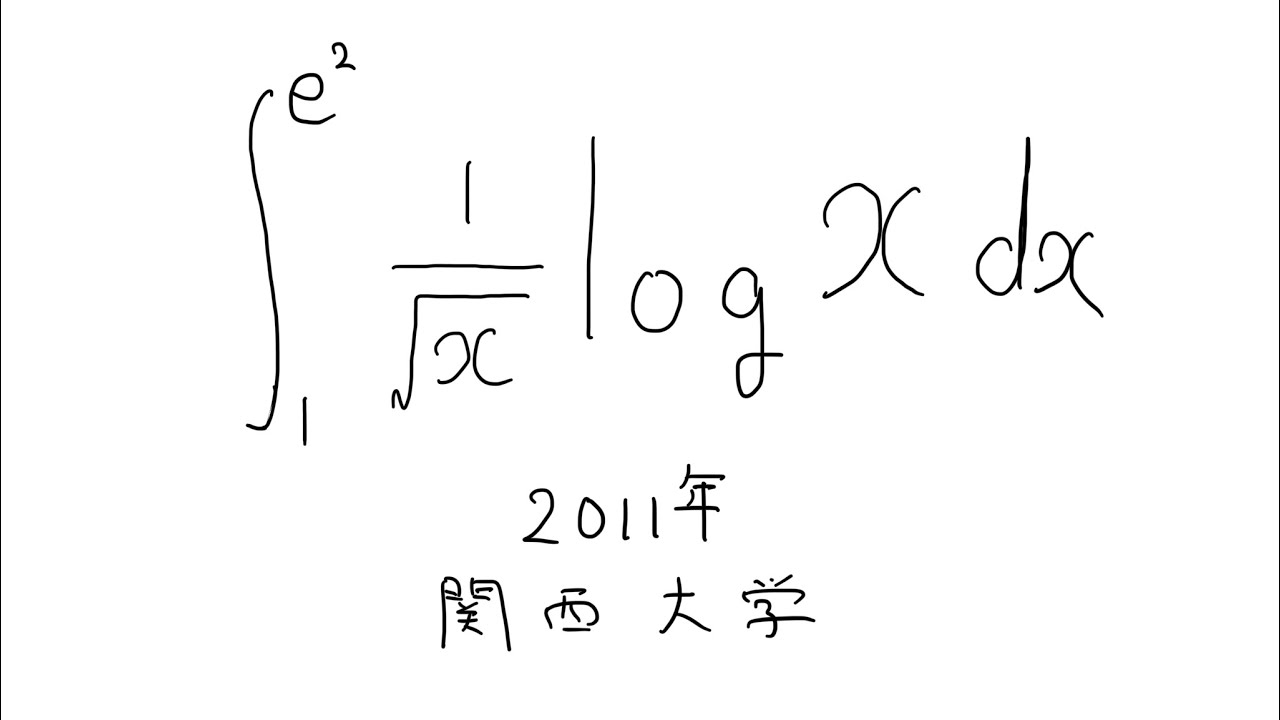
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e^2} \displaystyle \frac{1}{\sqrt{ x }} log_x\ dx$
出典：2011年関西大学
この動画を見る
$\displaystyle \int_{1}^{e^2} \displaystyle \frac{1}{\sqrt{ x }} log_x\ dx$
出典：2011年関西大学
【高校数学】毎日積分54日目 実践編⑤回転体シリーズ~斜めで、切り取って、最短距離のフルコース~【難易度：★★★★★】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$xyz$空間内において、連立不等式
$\frac{x^2}{4}+y^2≦1 , |z|≦6$
により定まる領域を$V$とし、2点$（2,0,2），（-2,0,-2）$を通る直線を$l$とする。
（1）$|t|≦2\sqrt2$を満たす実数tに対し、点$P_t（\frac{t}{\sqrt{2}},0,\frac{t}{\sqrt{2}})$を通り$l$に重直な平面を$H_t$とする。また、実数$\theta$に対し、点$（2\cos\theta,\sin\theta,0）$を通り$z$軸に平行な直線を$L_{\theta}$とする。$L_{\theta}$と$H_t$との交点の$z$座標を$t$と$\theta$を用いて表せ。
（2） $l$を回転軸に持つ回転体で$V$に含まれるものを考える。このような回転体のうちで体積が最大となるものの体積を求めよ。
【東京工業大学 2018】
この動画を見る
$xyz$空間内において、連立不等式
$\frac{x^2}{4}+y^2≦1 , |z|≦6$
により定まる領域を$V$とし、2点$（2,0,2），（-2,0,-2）$を通る直線を$l$とする。
（1）$|t|≦2\sqrt2$を満たす実数tに対し、点$P_t（\frac{t}{\sqrt{2}},0,\frac{t}{\sqrt{2}})$を通り$l$に重直な平面を$H_t$とする。また、実数$\theta$に対し、点$（2\cos\theta,\sin\theta,0）$を通り$z$軸に平行な直線を$L_{\theta}$とする。$L_{\theta}$と$H_t$との交点の$z$座標を$t$と$\theta$を用いて表せ。
（2） $l$を回転軸に持つ回転体で$V$に含まれるものを考える。このような回転体のうちで体積が最大となるものの体積を求めよ。
【東京工業大学 2018】
大学入試問題#725「計算ミスだけ注意」 早稲田商学部(2015) 対数と三角関数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
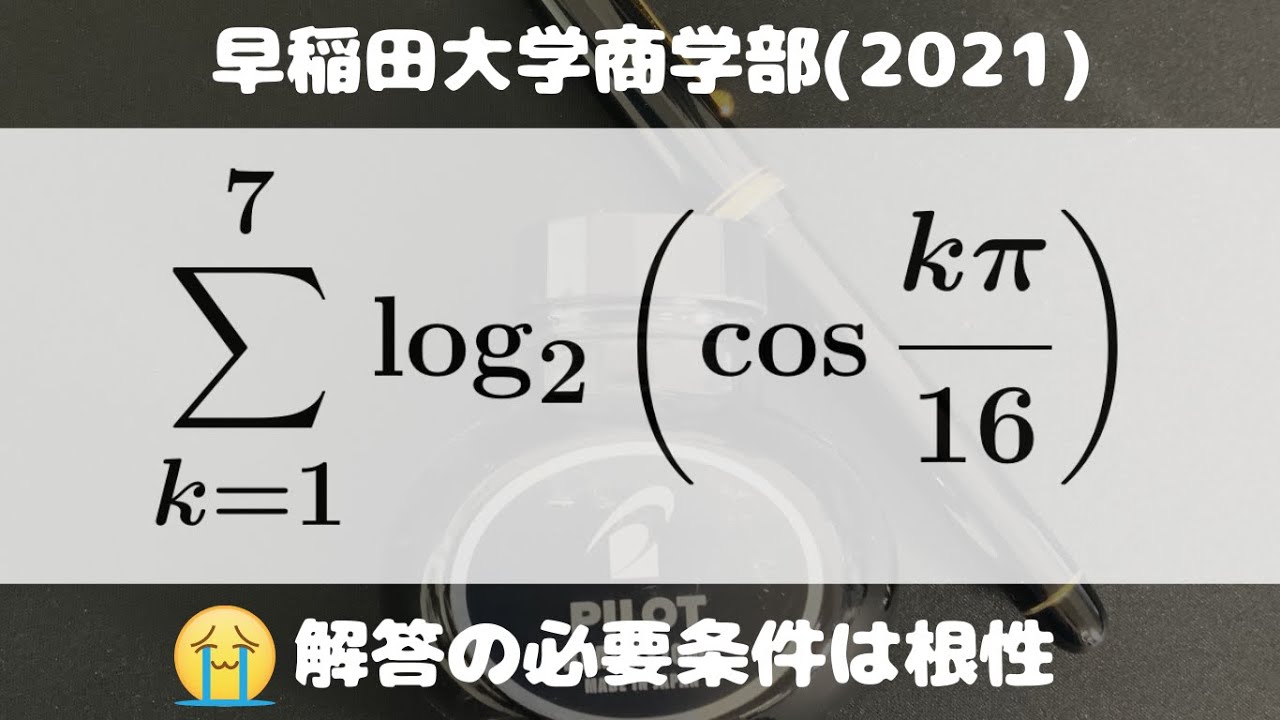
$\displaystyle \sum_{k=1}^7 log_2(\cos\displaystyle \frac{k\pi}{16})$
出典：2021年早稲田大学商学部 入試問題
この動画を見る
$\displaystyle \sum_{k=1}^7 log_2(\cos\displaystyle \frac{k\pi}{16})$
出典：2021年早稲田大学商学部 入試問題
大学入試問題#724「教科書の例題」 千葉大学(2023) 積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=x^2+\displaystyle \int_{-1}^{2} (xf(t)-t)dt$を満たす関数$f(x)$を求めよ
出典：2023年千葉大学 入試問題
この動画を見る
$f(x)=x^2+\displaystyle \int_{-1}^{2} (xf(t)-t)dt$を満たす関数$f(x)$を求めよ
出典：2023年千葉大学 入試問題
大学入試問題#723「いつもとタイプが違う」 一橋大学(2023)整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ m }+\sqrt{ n }=\sqrt{ 2023 }$を満たす自然数の組$(m,n)$の個数を求めよ。
出典：2023年一橋大学後期 入試問題
この動画を見る
$\sqrt{ m }+\sqrt{ n }=\sqrt{ 2023 }$を満たす自然数の組$(m,n)$の個数を求めよ。
出典：2023年一橋大学後期 入試問題
大学入試問題#722「これはミスれん！」 千葉大学(2023)定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{a}^{b} (x-a)^3(x-b) dx$
ただし、$a,b$は定数とする
出典：2023年千葉大学
この動画を見る
$\displaystyle \int_{a}^{b} (x-a)^3(x-b) dx$
ただし、$a,b$は定数とする
出典：2023年千葉大学
関西医科大学 2011 極限
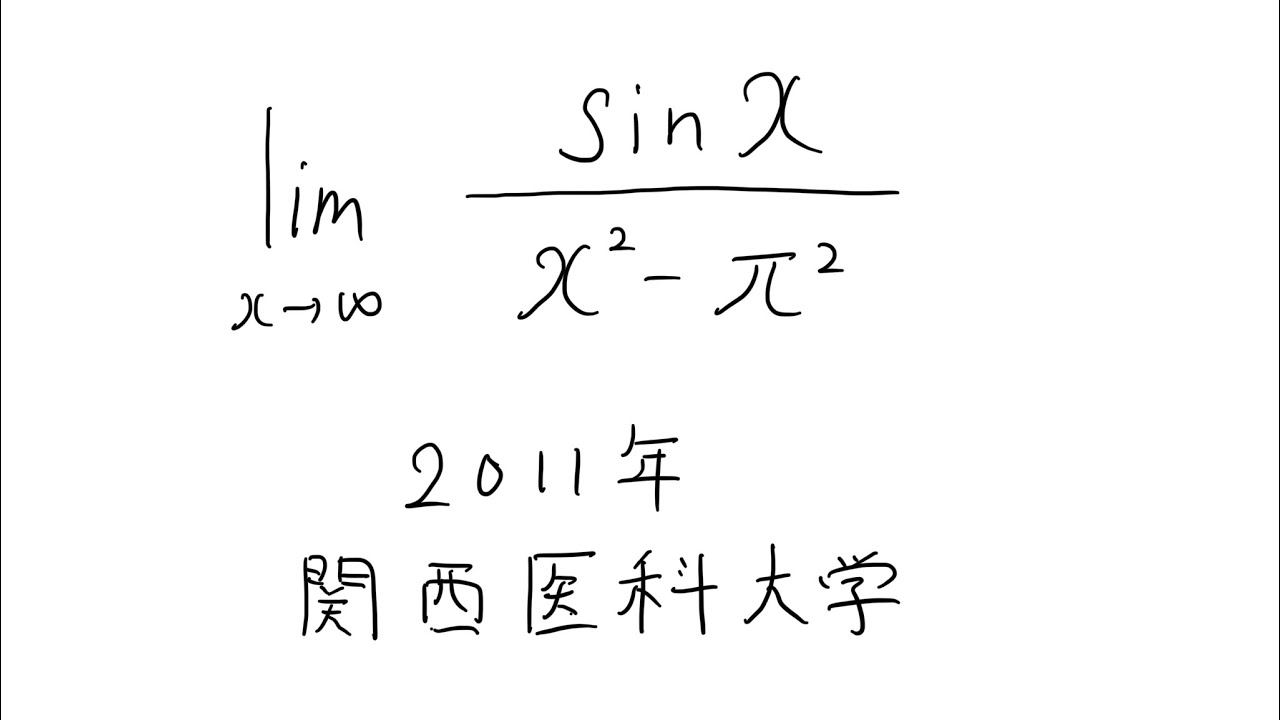
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$
出典：2011年関西医科大学
この動画を見る
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$
出典：2011年関西医科大学
大学入試問題#721「落ち着いて計算」 早稲田商学部(2012) 積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
定数関数でない関数$f(x)$が
$f(x)=x^2-\displaystyle \int_{0}^{1}(f(t)+x)^2 dt$を満たすとき$f(x)$を求めよ。
出典：2012年早稲田大学商学部 入試問題
この動画を見る
定数関数でない関数$f(x)$が
$f(x)=x^2-\displaystyle \int_{0}^{1}(f(t)+x)^2 dt$を満たすとき$f(x)$を求めよ。
出典：2012年早稲田大学商学部 入試問題
大学入試問題#720「正面突破はしんどい？」 電気通信大学(2023) y軸回転体
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京電機大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \leq x \leq 1$で定まる関数
$f(x)=\sqrt{ 1-x^2 }+\displaystyle \frac{x}{2}-1$において、$y=f(x)$と$x$軸で囲まれた部分を、$y$軸の周りに1回転して得られる体積$V$を求めよ。
出典：2023年電気通信大学 入試問題
この動画を見る
$0 \leq x \leq 1$で定まる関数
$f(x)=\sqrt{ 1-x^2 }+\displaystyle \frac{x}{2}-1$において、$y=f(x)$と$x$軸で囲まれた部分を、$y$軸の周りに1回転して得られる体積$V$を求めよ。
出典：2023年電気通信大学 入試問題
2024年共通テスト徹底解説〜数学ⅡB第5問ベクトル〜福田の入試問題解説
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数C
指導講師：
福田次郎
問題文全文(内容文)：
共通テスト2024の数学ⅡB第5問ベクトルを徹底解説します
この動画を見る
共通テスト2024の数学ⅡB第5問ベクトルを徹底解説します
大学入試問題#719「これは落としたくない」 早稲田大学商学部(2005) 3次方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
3次方程式
$x^3-px^2+11x-q=0$が3つの連続する正の整数を解とするとき、$p,q$の値を求めよ。
出典：2005年早稲田大学商学部 入試問題
この動画を見る
3次方程式
$x^3-px^2+11x-q=0$が3つの連続する正の整数を解とするとき、$p,q$の値を求めよ。
出典：2005年早稲田大学商学部 入試問題
2024年共通テスト徹底解説〜数学ⅠA第2問(1)2次関数〜福田の入試問題解説
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師：
福田次郎
問題文全文(内容文)：
共通テスト2024の数学ⅠA第2問(2)2次関数を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅠA第2問(2)2次関数を徹底解説します
2024共通テスト過去問
大学入試問題#718「理系の偏差値63ではきつい」 早稲田商学部(2011) 微積の応用
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\displaystyle \int_{0}^{1} |t^2-x^2|dt$の最小値を求めよ。
出典：2011年早稲田大学商学部 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{1} |t^2-x^2|dt$の最小値を求めよ。
出典：2011年早稲田大学商学部 入試問題
昭和大学医学部 2018年 区分求積法 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n (\displaystyle \frac{\sqrt{ n }}{n+k})^2$
出典：2018年昭和大学医学部
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n (\displaystyle \frac{\sqrt{ n }}{n+k})^2$
出典：2018年昭和大学医学部
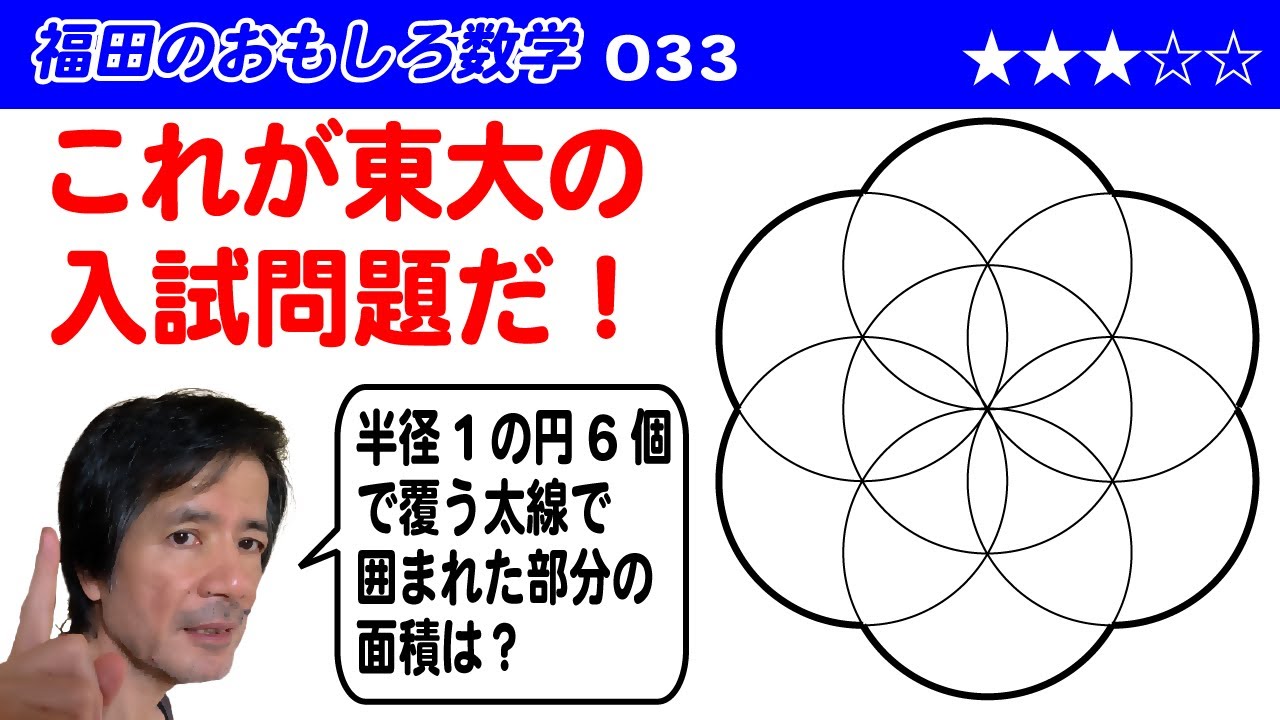
福田のおもしろ数学033〜これが東大の入試問題だ！〜6個の円がおおう範囲の面積
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
これが東大の入試問題だ！
半径1の円6個で覆う太線で囲まれた部分の面積を求めよ
図は動画内参照
東京大学過去問
この動画を見る
これが東大の入試問題だ！
半径1の円6個で覆う太線で囲まれた部分の面積を求めよ
図は動画内参照
東京大学過去問
大学入試問題#717「これはよく考えられた問題だな～～」 早稲田商学部(2012) 対数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$log_3\ x-\displaystyle \frac{1}{log_9\ x}=(-1)^x$を満たす正の整数$x$の値を求めよ。
出典：2012年早稲田大学商学部 入試問題
この動画を見る
$log_3\ x-\displaystyle \frac{1}{log_9\ x}=(-1)^x$を満たす正の整数$x$の値を求めよ。
出典：2012年早稲田大学商学部 入試問題
2024年共通テスト徹底解説〜数学ⅡB第4問数列〜福田の入試問題解説
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師：
福田次郎
問題文全文(内容文)：
共通テスト2024の数学ⅡB第4問数列を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第4問数列を徹底解説します
2024共通テスト過去問
大学入試問題#716「文系にはきつくね？」 早稲田商学部(2015) 数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
数列$\{a_n\}$は次の条件$(i),(ii)$を満たす
（$i$）$a_1=0,\ a_n \leq 0(n=2,3,4・・・)$
（$ii$）$n=\displaystyle \int_{a_n}^{a_{n+1}} (x+\displaystyle \frac{1}{2})dx(n=1,2,3,・・・)$
$n=2,3,4,・・・$のとき、$a_n$を求めよ
出典：2015年早稲田大学商学部 入試問題
この動画を見る
数列$\{a_n\}$は次の条件$(i),(ii)$を満たす
（$i$）$a_1=0,\ a_n \leq 0(n=2,3,4・・・)$
（$ii$）$n=\displaystyle \int_{a_n}^{a_{n+1}} (x+\displaystyle \frac{1}{2})dx(n=1,2,3,・・・)$
$n=2,3,4,・・・$のとき、$a_n$を求めよ
出典：2015年早稲田大学商学部 入試問題
大学入試問題#715「このタイプ苦手」 早稲田理工系学部(2021) 整式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=x^4-x^2+1$
１．$x^6$を$f(x)$で割ったときの余りを求めよ
２．$x^{2021}$を$f(x)$で割ったときの余りを求めよ
３．自然数$n$が3の倍数の時、$(x^2-1)^n-1$が$f(x)$で割り切れることを示せ
出典：2021年早稲田大学理工学部 入試問題
この動画を見る
$f(x)=x^4-x^2+1$
１．$x^6$を$f(x)$で割ったときの余りを求めよ
２．$x^{2021}$を$f(x)$で割ったときの余りを求めよ
３．自然数$n$が3の倍数の時、$(x^2-1)^n-1$が$f(x)$で割り切れることを示せ
出典：2021年早稲田大学理工学部 入試問題
大学入試問題#714「The basic integral problem」 青山学院大(2021) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{5} \displaystyle \frac{dx}{(x+3)\sqrt{ x+1 }}$
出典：2021年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{5} \displaystyle \frac{dx}{(x+3)\sqrt{ x+1 }}$
出典：2021年青山学院大学 入試問題