その他
その他
07愛知県教員採用試験（数学：9番 整数問題、二項定理）
07愛知県教員採用試験（数学：7番 複素数）
単元：
#数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{7}$ $\vert Z \vert=1,Z^5=1$
$Z\leftarrow \in $を求めよ.
この動画を見る
$\boxed{7}$ $\vert Z \vert=1,Z^5=1$
$Z\leftarrow \in $を求めよ.
04愛知県教員採用試験（数学：10番 重積分）
単元：
#積分とその応用#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\iint_D f \ x \ dx\ dy$
$ D:\sqrt{\dfrac{x}{4}}+\sqrt{\dfrac{y}{3}}\leqq 1 $
これを解け.
図は動画内参照
この動画を見る
$\iint_D f \ x \ dx\ dy$
$ D:\sqrt{\dfrac{x}{4}}+\sqrt{\dfrac{y}{3}}\leqq 1 $
これを解け.
図は動画内参照
04愛知県教員採用試験（数学：14番 楕円、接線、相加相乗平均）
単元：
#微分とその応用#接線と法線・平均値の定理#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{14}$ $a\gt 0,b\gt 0$
楕円$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
の接線がx軸,y軸と交わる点を$P.Q$とする.
$PQ$の最小値を求めよ.
この動画を見る
$\boxed{14}$ $a\gt 0,b\gt 0$
楕円$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
の接線がx軸,y軸と交わる点を$P.Q$とする.
$PQ$の最小値を求めよ.
07神奈川県教員採用試験（数学：9番 領域と最小値）
単元：
#数Ⅱ#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{9}$
$x^2+xy-2y^2+6y-4\geqq 0$
$x^2+y^2$の最小値を求めよ.
この動画を見る
$\boxed{9}$
$x^2+xy-2y^2+6y-4\geqq 0$
$x^2+y^2$の最小値を求めよ.
練習問題9（数検準1級 教員採用試験 極限値からの区分求積法）【難】
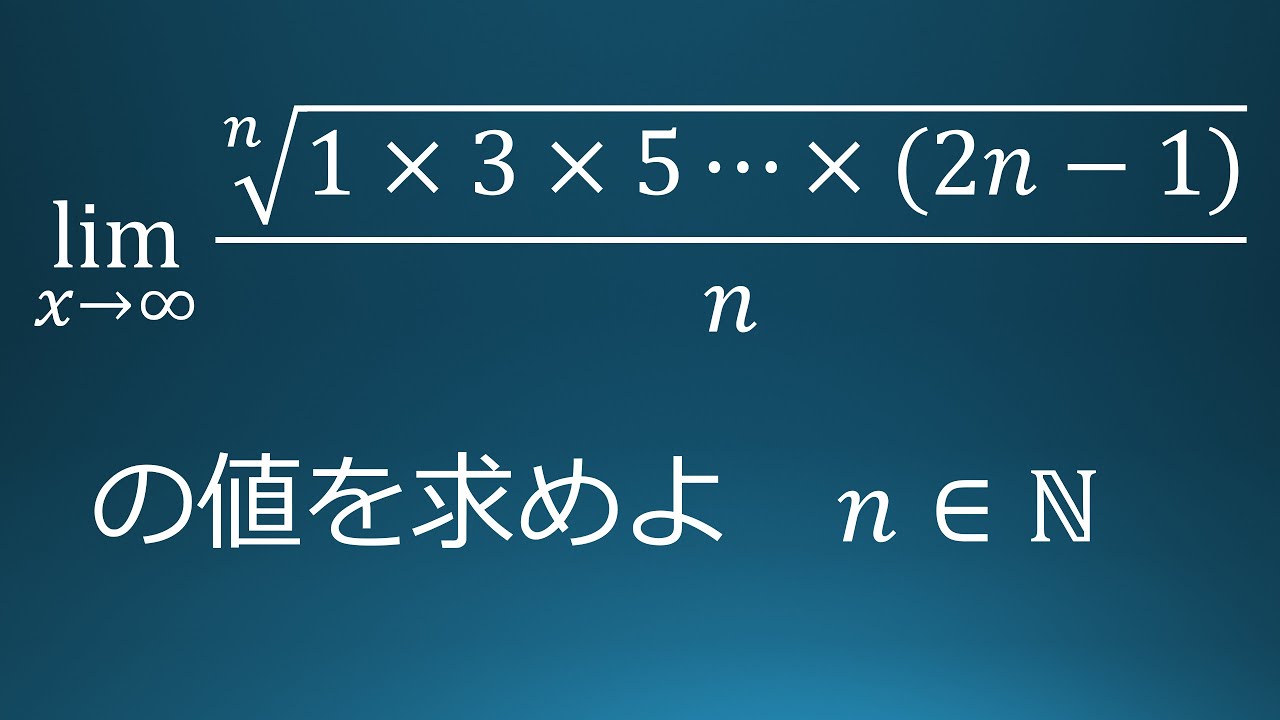
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
限値からの区分求積法を解説していきます.
この動画を見る
限値からの区分求積法を解説していきます.
練習問題8（数検準1級 教員採用試験 極限値からの区分求積法）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \dfrac{\sqrt[n]{1\times 3\times 5\times ･･･ \times(2n-1)}}{n}$
これを解け.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{\sqrt[n]{1\times 3\times 5\times ･･･ \times(2n-1)}}{n}$
これを解け.
練習問題7（数検準1級 教員採用試験 極限値）
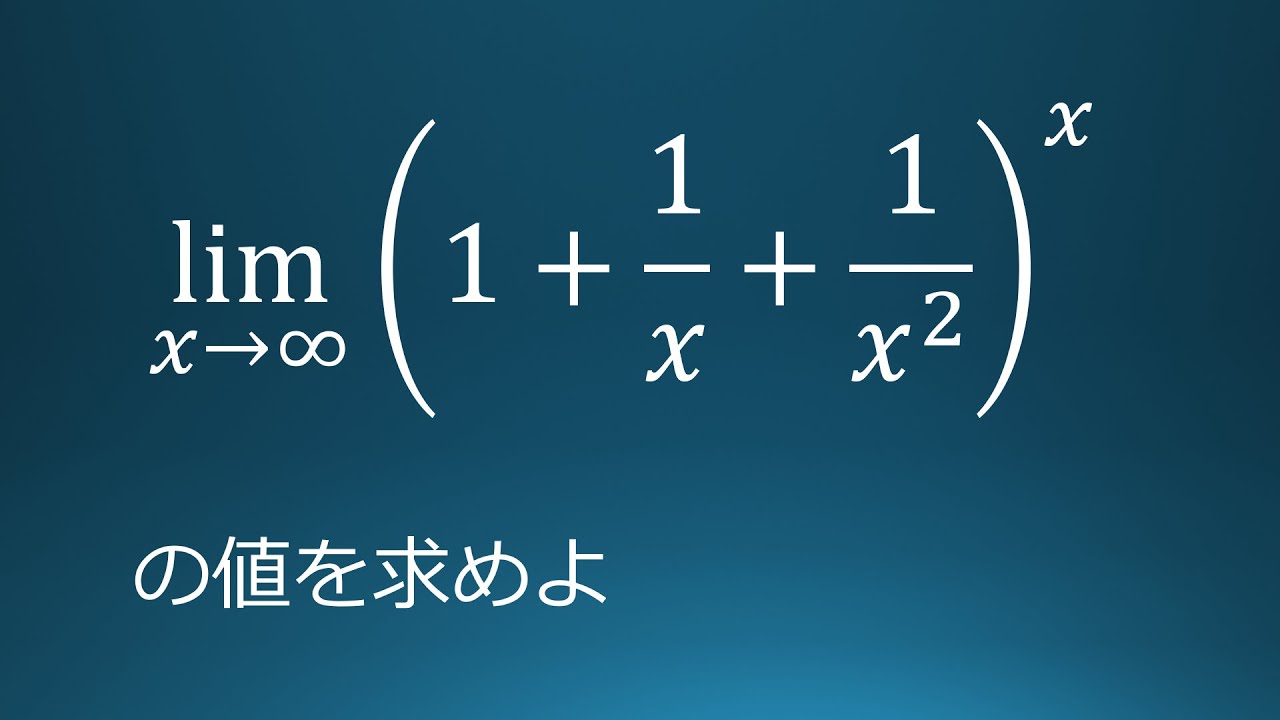
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} \left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)^x$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\infty} \left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)^x$
これを解け.
数学の計算ミスを減らす３つのコツ～全国模試1位の勉強法【篠原好】
練習問題5（数検準1級 教員採用試験 極限値）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} \dfrac{\tan^3x-\sin^3x}{x^5}$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\infty} \dfrac{\tan^3x-\sin^3x}{x^5}$
これを解け.
07兵庫県教員採用試験（数学：7番 三角関数の積分）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$ $k\gt 0,y=\sin x,y=k\ \cos x$
直線$x=0,x=\dfrac{\pi}{2}$で囲まれた部分の面積$S$を$k$を用いて表せ.
図は動画内参照
この動画を見る
$\boxed{5}$ $k\gt 0,y=\sin x,y=k\ \cos x$
直線$x=0,x=\dfrac{\pi}{2}$で囲まれた部分の面積$S$を$k$を用いて表せ.
図は動画内参照
数学の参考書・問題集、やるべきは？「網羅系」or「集約系」？～全国模試1位の勉強法【篠原好】
単元：
#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
数学の参考書・問題集
「やるべきは「網羅系」or「集約系」か」についてお話しています。
この動画を見る
数学の参考書・問題集
「やるべきは「網羅系」or「集約系」か」についてお話しています。
08愛知県教員採用試験（数学：9番 区分求積法）
08愛知県教員採用試験（数学：10番 微分方程式）
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}$ $$f'(x)-2\ f(x)-2=0$
$f(0)=9$のとき,$f(1)$を求めよ.(解)
この動画を見る
$\boxed{10}$ $$f'(x)-2\ f(x)-2=0$
$f(0)=9$のとき,$f(1)$を求めよ.(解)
05神奈川県教員採用試験（数学：2番 対数）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$ $17^{50}$は$62$桁の整数である.
$17^{24}$の桁数を求めよ.
この動画を見る
$\boxed{2}$ $17^{50}$は$62$桁の整数である.
$17^{24}$の桁数を求めよ.
11神奈川県教員採用試験（数学：8番 三角関数）
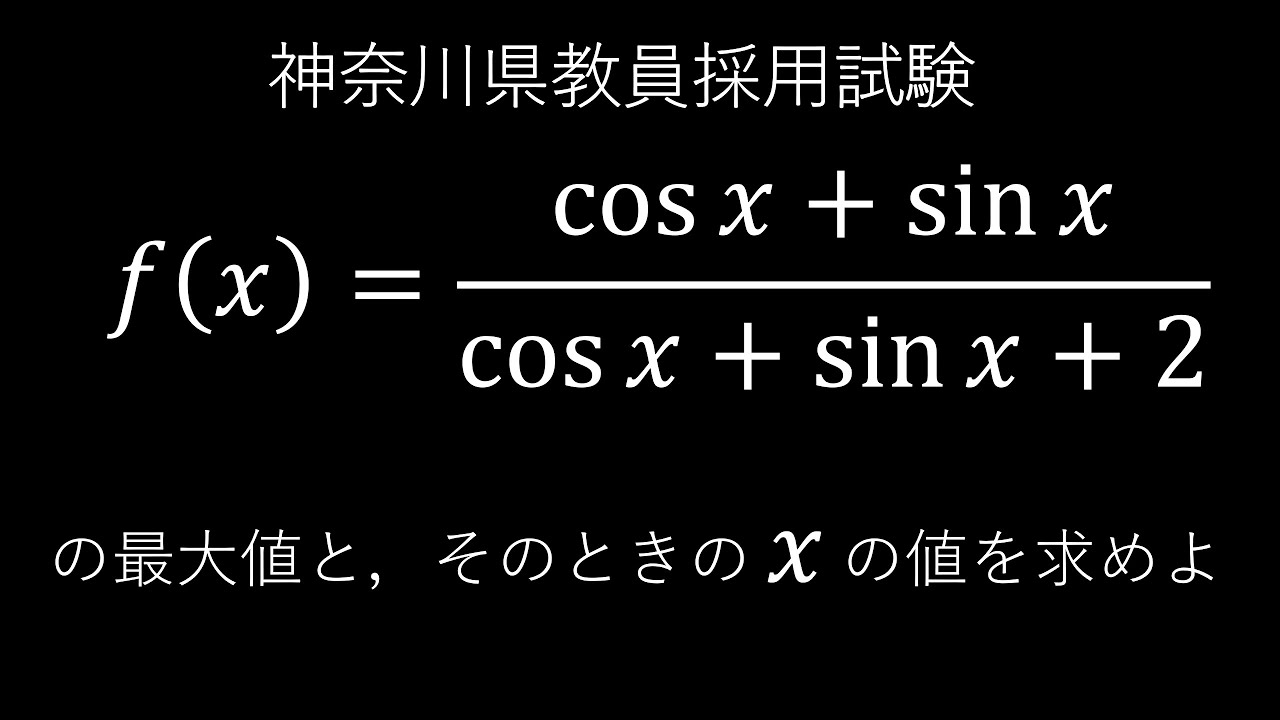
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{8}$ $f(x)~\dfrac{\cos x+\sin x}{\cos x+\sin x+2}$の最大値とそのときの値を求めよ.
この動画を見る
$\boxed{8}$ $f(x)~\dfrac{\cos x+\sin x}{\cos x+\sin x+2}$の最大値とそのときの値を求めよ.
08愛知県教員採用試験（数学：4番 数列）
単元：
#数列#数列とその和（等差・等比・階差・Σ）#その他#数学(高校生)#数B#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n$である.
$\displaystyle \lim_{ n \to \infty }\dfrac{a_{n-1}}{a_n}$の値を求めよ.
この動画を見る
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n$である.
$\displaystyle \lim_{ n \to \infty }\dfrac{a_{n-1}}{a_n}$の値を求めよ.
05愛知県教員採用試験（数学：1番 気合の式変形）
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$ $x^2-x-1=0$の解を$\alpha,\beta(\alpha\gt \beta)$とする.
(1)$\alpha^{n+2}-\beta^{n+2}=\alpha^{n+1}-\beta^{n+1}+\alpha^n-\beta^n$を示せ.
$(n\in IN)$
(2)$\alpha^7-\beta^7$の値を求めよ.
この動画を見る
$\boxed{1}$ $x^2-x-1=0$の解を$\alpha,\beta(\alpha\gt \beta)$とする.
(1)$\alpha^{n+2}-\beta^{n+2}=\alpha^{n+1}-\beta^{n+1}+\alpha^n-\beta^n$を示せ.
$(n\in IN)$
(2)$\alpha^7-\beta^7$の値を求めよ.
奈良県教員採用試験（数学：式変形）
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$x+y+z=2$ , $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{2}$
のとき
$\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}$の値を求めよ。
この動画を見る
$x+y+z=2$ , $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{2}$
のとき
$\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}$の値を求めよ。
数学のチャート式はコンパス何までやるべきか？～全国模試1位の勉強法【篠原好】
単元：
#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
「数学のチャート式はコンパス何までやるべきか？」についてお話しています。
この動画を見る
「数学のチャート式はコンパス何までやるべきか？」についてお話しています。
09愛知県教員採用試験（数学：2番 微積）
単元：
#関数と極限#微分とその応用#積分とその応用#関数の極限#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
2⃣ $0 \leqq x \leqq \frac{1}{\sqrt 3}$
$f(x)=\int_x^{\sqrt 3 x} \sqrt{1-t^2} dt$
(1)f(x)の最大値
(2)$\displaystyle \lim_{ x \to \infty } \frac{f(x)}{x}$
この動画を見る
2⃣ $0 \leqq x \leqq \frac{1}{\sqrt 3}$
$f(x)=\int_x^{\sqrt 3 x} \sqrt{1-t^2} dt$
(1)f(x)の最大値
(2)$\displaystyle \lim_{ x \to \infty } \frac{f(x)}{x}$
04大阪府教員採用試験（数学：3番 複素数）
単元：
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
3⃣ $Z_1,Z_2 \in \mathbb{C}$
$|Z_1|=|Z_2|=|Z_1+Z_2|=1$ ⇒ $Z_1^{3}=Z_2^{3}$を示せ
この動画を見る
3⃣ $Z_1,Z_2 \in \mathbb{C}$
$|Z_1|=|Z_2|=|Z_1+Z_2|=1$ ⇒ $Z_1^{3}=Z_2^{3}$を示せ
練習問題3（数検準1級，教員採用試験 対数と相加相乗平均）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#指数関数と対数関数#恒等式・等式・不等式の証明#対数関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt x+ \sqrt y = 20$
$log_{10}x+log_{10}y$の最大値を求めよ。
この動画を見る
$\sqrt x+ \sqrt y = 20$
$log_{10}x+log_{10}y$の最大値を求めよ。
08神奈川県教員採用試験（数学：10番 式変形）
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}$ $x,y ＞0$
$\sqrt x + \sqrt y \leqq k \sqrt{3x+y}$
をみたすkの最小値を求めよ
この動画を見る
$\boxed{10}$ $x,y ＞0$
$\sqrt x + \sqrt y \leqq k \sqrt{3x+y}$
をみたすkの最小値を求めよ
06神奈川県教員採用試験（数学：1番 数列の極限）
単元：
#関数と極限#数列の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
1⃣$a_1=1,\frac{(a_{n+1})^2}{a_n} = \frac{1}{e}$
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ。
この動画を見る
1⃣$a_1=1,\frac{(a_{n+1})^2}{a_n} = \frac{1}{e}$
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ。
重積分⑫-2【図形Dの重心】（高専数学 微積II，数検1級1次解析対応）
単元：
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定1級#その他#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
図形Dの重心Ｇは
$G\begin{pmatrix}
∬_Dxdxdy & ∬_Dydxdy \\
∬_Ddxdy & ∬_Ddxdy
\end{pmatrix}$
(1)$y^2=4x,x=1$
で囲まれた図形Dの重心Gを求めよ。
(2)$\sqrt x+\sqrt y =1$,x軸、y軸で囲まれた図形Dの重心Gを求めよ。
この動画を見る
図形Dの重心Ｇは
$G\begin{pmatrix}
∬_Dxdxdy & ∬_Dydxdy \\
∬_Ddxdy & ∬_Ddxdy
\end{pmatrix}$
(1)$y^2=4x,x=1$
で囲まれた図形Dの重心Gを求めよ。
(2)$\sqrt x+\sqrt y =1$,x軸、y軸で囲まれた図形Dの重心Gを求めよ。
重積分⑫-1【図形Dの重心】（高専数学 微積II，数検1級1次解析対応）
単元：
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定1級#その他#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
平面上の図形Dの重心Gは
$G\begin{pmatrix}
∬_Dxdxdy & ∬_Dydxdy \\
∬_Ddxdy & ∬_Ddxdy
\end{pmatrix}$
△OABの重心Gは
$G(\frac{0+3+3}{3},\frac{0+0+3}{3})$
$G(2,1)$
＊図は動画内参照
この動画を見る
平面上の図形Dの重心Gは
$G\begin{pmatrix}
∬_Dxdxdy & ∬_Dydxdy \\
∬_Ddxdy & ∬_Ddxdy
\end{pmatrix}$
△OABの重心Gは
$G(\frac{0+3+3}{3},\frac{0+0+3}{3})$
$G(2,1)$
＊図は動画内参照
練習問題１（数検準1級、教員採用試験 数列の極限）
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#その他#数学検定#数学検定準1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$a_2=a_1=1$
$a_{n+2}=a_{n+1}+a_n$
$\displaystyle \lim_{ n \to \infty } \frac{loga_n}{n}$を求めよ。
この動画を見る
$a_2=a_1=1$
$a_{n+2}=a_{n+1}+a_n$
$\displaystyle \lim_{ n \to \infty } \frac{loga_n}{n}$を求めよ。
重積分⑪【f(x,y)の領域Dにおける平均】（高専数学 微積II，数検1級1次解析対応）
単元：
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$Z=f(x,y)$のDにおける平均
${}^{\exists}h \in \mathbb{R}$
$h×D=∬_D f(x,y)dxdy$
この動画を見る
$Z=f(x,y)$のDにおける平均
${}^{\exists}h \in \mathbb{R}$
$h×D=∬_D f(x,y)dxdy$
05大阪府教員採用試験（数学：2番 指数対数）
単元：
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
2⃣ $x,y,z \in \mathbb{R}$
$2^x=3^y=Z$
$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$のときZの値を求めよ。
この動画を見る
2⃣ $x,y,z \in \mathbb{R}$
$2^x=3^y=Z$
$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$のときZの値を求めよ。