 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
高校入試だけど多項定理 江戸川学園取手

【高校数学】三角比を使った三角形の面積の求め方 3-9【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【高校数学】三角比を使った三角形の面積の求め方を解説していきます。
$\triangle ABC$の面積$S$を求めよ。
(1)$b=4,c=7,A=45°$
(2)$a=7,b=5,c=8$
この動画を見る
【高校数学】三角比を使った三角形の面積の求め方を解説していきます。
$\triangle ABC$の面積$S$を求めよ。
(1)$b=4,c=7,A=45°$
(2)$a=7,b=5,c=8$
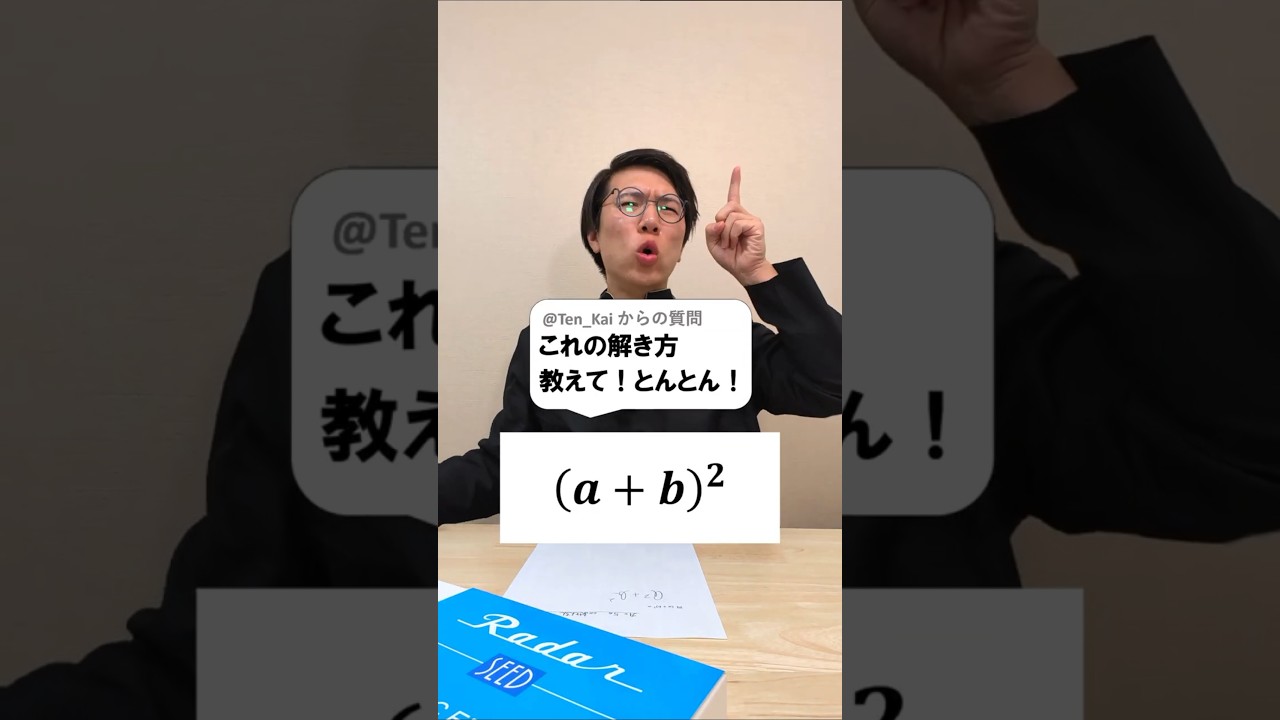
これなにが間違い?
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(a+b)^2$のどこが間違いか解説していきます。
この動画を見る
$(a+b)^2$のどこが間違いか解説していきます。
【数Ⅰ】【図形と計量】0°≦θ≦180°とする。次の不等式を満たすもの値の範囲を求めよ。-1<√3 tanθ <3 (他8問)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0^\circ \leq \theta \leq 180^\circ$とする。
次の不等式を満たす$\theta$ の値の範囲を求めよ。
$\sin\theta > \dfrac{1}{\sqrt{2}}$
$\sin\theta \leq \dfrac{1}{2}$
$\cos\theta \leq -\dfrac{\sqrt{3}}{2}$
$\cos\theta < -\dfrac{1}{\sqrt{2}}$
$0 < \tan\theta \leq 1$
$\tan\theta \geq \sqrt{3}$
$1 < 2\sin\theta \leq \sqrt{3}$
$1 \leq -2\cos\theta < \sqrt{3}$
$-1 < \sqrt{3}\tan\theta < 3$
この動画を見る
$0^\circ \leq \theta \leq 180^\circ$とする。
次の不等式を満たす$\theta$ の値の範囲を求めよ。
$\sin\theta > \dfrac{1}{\sqrt{2}}$
$\sin\theta \leq \dfrac{1}{2}$
$\cos\theta \leq -\dfrac{\sqrt{3}}{2}$
$\cos\theta < -\dfrac{1}{\sqrt{2}}$
$0 < \tan\theta \leq 1$
$\tan\theta \geq \sqrt{3}$
$1 < 2\sin\theta \leq \sqrt{3}$
$1 \leq -2\cos\theta < \sqrt{3}$
$-1 < \sqrt{3}\tan\theta < 3$
【数Ⅰ】【図形と計量】sinθ+cosθ=1/3のとき(1) sinθcosθの値(2) sin³θ+cos³θの値(3) sinθ-cosθの値

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
sinθ+cosθ=1/3のとき
(1) sinθcosθの値
(2) sin³θ+cos³θの値
(3) sinθ-cosθの値
この動画を見る
sinθ+cosθ=1/3のとき
(1) sinθcosθの値
(2) sin³θ+cos³θの値
(3) sinθ-cosθの値
【数Ⅰ】【図形と計量】(1)cos36°を求めよ(2)正五角形の対角線の長さを求めよ。

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)cos36°を求めよ
(2)正五角形の対角線の長さを求めよ。
この動画を見る
(1)cos36°を求めよ
(2)正五角形の対角線の長さを求めよ。
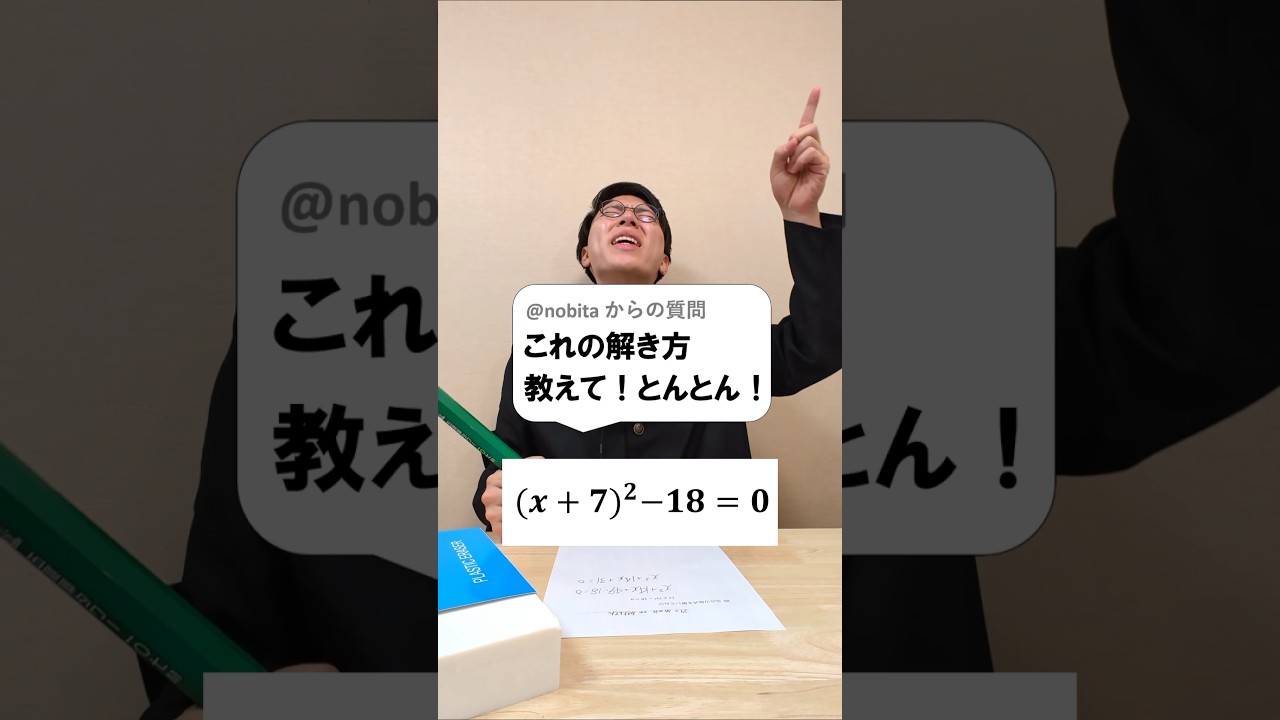
このタイプの2次方程式の解き方は?
【数Ⅰ】【2次関数】不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。
この動画を見る
不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。
【数Ⅰ】【2次関数】aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
この動画を見る
aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
√5の小数部分は?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt5$の小数部分は?
この動画を見る
$\sqrt5$の小数部分は?
【数Ⅰ】【2次関数】(1) y=|x²+2x|のグラフを描け。(2) |x²+2x|=k の実数解の個数を求めよ。

これの何が間違い?

【数Ⅰ】【2次関数】グラフを利用して、次の不等式を解け。(1) |x+1|<2x (2) |x²-4| >-3x

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
グラフを利用して、次の不等式を解け。
(1) |x+1|<2x
(2) |x²-4| >-3x
この動画を見る
グラフを利用して、次の不等式を解け。
(1) |x+1|<2x
(2) |x²-4| >-3x
【数Ⅰ】【2次関数】x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
この動画を見る
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
【数Ⅰ】【2次関数】x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
この動画を見る
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
【数Ⅰ】【データの分析】672、693、644、665、630、644でc=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。変量uとxの平均値、分散、標準偏差を求めよ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量xのデータが次のように与えられている。
672,693、644、665、630、644
c=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
この動画を見る
変量xのデータが次のように与えられている。
672,693、644、665、630、644
c=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
【数Ⅰ】【データの分析】あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。生徒全員の得点を2.5倍して、30点を加えたとき、平均値、分散、標準偏差を求めよ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。得点調整のため、生徒全員の得点を2.5倍して、更に30点を加えたとき、得点調整後の平均値、分散、標準偏差を求めよ。
この動画を見る
あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。得点調整のため、生徒全員の得点を2.5倍して、更に30点を加えたとき、得点調整後の平均値、分散、標準偏差を求めよ。
【数Ⅰ】【データの分析】変量Xのデータの平均値xが35、分散Sx²が16で新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ(1)y=x-10(2)y=3x(3)y=-x/2+6

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量Xのデータの平均値xが35、分散Sx²が16であるとする。
このとき、次の式によってえられる新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ。
(1)y=x-10
(2)y=3x
(3)y=-x/2+6
この動画を見る
変量Xのデータの平均値xが35、分散Sx²が16であるとする。
このとき、次の式によってえられる新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ。
(1)y=x-10
(2)y=3x
(3)y=-x/2+6
【数Ⅰ】【2次関数】次の条件を満たすような定数a の値の範囲を求めよ。(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。他1問

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たすような定数a の値の範囲を求めよ。
(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。
(2) 二次方程式 2ax²-(a+2)x-5=0 の1つの解が -1<x<0 の範囲にあり、他の解が 2<x<3 の範囲にある。ただし a>0 とする。
この動画を見る
次の条件を満たすような定数a の値の範囲を求めよ。
(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。
(2) 二次方程式 2ax²-(a+2)x-5=0 の1つの解が -1<x<0 の範囲にあり、他の解が 2<x<3 の範囲にある。ただし a>0 とする。
【数Ⅰ】【2次関数】a<b<c のとき(x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)=0の2つの解のうち1つは a<x<b の範囲にありもう1つは b<x<c の範囲にあることを示せ

【数Ⅰ】【2次関数】放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
この動画を見る
放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
【数Ⅰ】【2次関数】放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
この動画を見る
放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
これ解ける?

単元:
#数Ⅰ#図形と計量#その他#数学(高校生)#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
長方形のケーキの中をランダムに長方形で取り除かれた。
どうやって二等分にできるのか?
マイクロソフトの入社試験過去問題
この動画を見る
長方形のケーキの中をランダムに長方形で取り除かれた。
どうやって二等分にできるのか?
マイクロソフトの入社試験過去問題
【数Ⅰ】【2次関数】次の関数に最大値・最小値があればそれを求めよ。(1) y=-2x⁴+4x²+3(2) y=(x²-2x)²+4(x²-2x)-1

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数に最大値・最小値があればそれを求めよ。
(1) y=-2x⁴+4x²+3
(2) y=(x²-2x)²+4(x²-2x)-1
この動画を見る
次の関数に最大値・最小値があればそれを求めよ。
(1) y=-2x⁴+4x²+3
(2) y=(x²-2x)²+4(x²-2x)-1
出た分野の授業します

福田のおもしろ数学577〜条件付きの最大を求める

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2x^2+3y^2+4z^2=1$のとき
$5x-6y+7z$の最大値と
そのときの$x,y,z$を求めよ。
この動画を見る
$2x^2+3y^2+4z^2=1$のとき
$5x-6y+7z$の最大値と
そのときの$x,y,z$を求めよ。
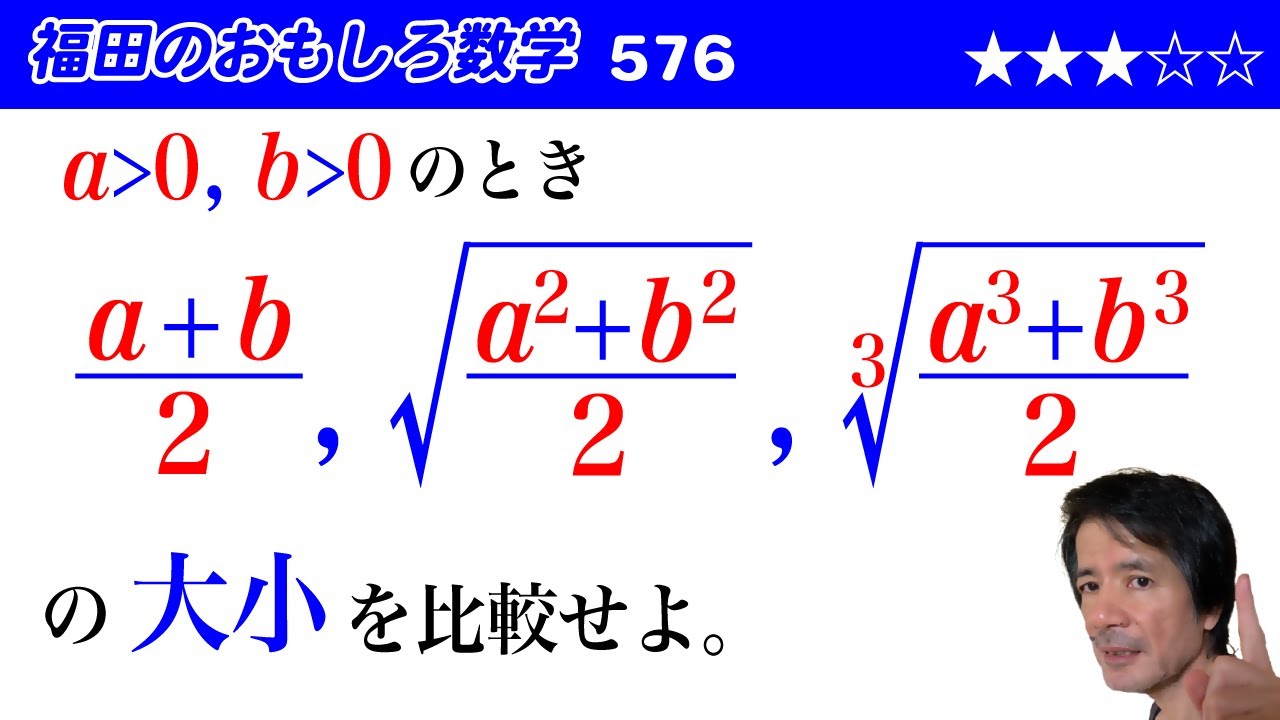
福田のおもしろ数学576〜累乗根の大小比較
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a\gt 0,b \gt 0$のとき
$\dfrac{a+b}{2},\sqrt{\dfrac{a^2+b^2}{2}},\sqrt[3]{\dfrac{a^3+b^3}{2}}$
の大小を比較せよ。
この動画を見る
$a\gt 0,b \gt 0$のとき
$\dfrac{a+b}{2},\sqrt{\dfrac{a^2+b^2}{2}},\sqrt[3]{\dfrac{a^3+b^3}{2}}$
の大小を比較せよ。
福田のおもしろ数学575〜3乗根のついた2重根号の計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt[3]{20+14\sqrt2}+\sqrt[3]{20-14\sqrt2}$
を簡単にして下さい。
この動画を見る
$\sqrt[3]{20+14\sqrt2}+\sqrt[3]{20-14\sqrt2}$
を簡単にして下さい。
福田のおもしろ数学574〜sin(x)がxのn次多項式で表せるか

二乗せよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a>b>0
a^2=2+√3
a^2=2-√3
ab=?
この動画を見る
a>b>0
a^2=2+√3
a^2=2-√3
ab=?
