 実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
 実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
1996 平成8年 大阪府

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
▢内に+-×÷のいずれかの記号を入れる。(同じ記号は何度使ってもよい)
$\sqrt{1▢9▢9▢6} =8$
1991大阪府
この動画を見る
▢内に+-×÷のいずれかの記号を入れる。(同じ記号は何度使ってもよい)
$\sqrt{1▢9▢9▢6} =8$
1991大阪府
簡単な計算問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\sqrt{\dfrac{2021^3-2019^3-2}{6}}$
この動画を見る
これを解け.
$\sqrt{\dfrac{2021^3-2019^3-2}{6}}$
福田の数学〜慶應義塾大学2021年看護医療学部第2問(3)〜絶対値の付いた2次不等式の解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(3)aを正の定数とし、不等式
$|x^2-ax+3| \leqq 1$
の解を実数の範囲で考える。
0 $\lt a \lt \boxed{\ \ ナ\ \ }$のとき、この不等式の解は存在しない。
$\boxed{\ \ ナ\ \ } \leqq a \leqq \boxed{\ \ ニ\ \ }$のとき、この不等式の解は
ある実数$p,q$によって$p \leqq x \leqq q$と表される。
$a \gt \boxed{\ \ ニ\ \ }$のときこの不等式の解は$\boxed{\ \ ヌ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{2}}$(3)aを正の定数とし、不等式
$|x^2-ax+3| \leqq 1$
の解を実数の範囲で考える。
0 $\lt a \lt \boxed{\ \ ナ\ \ }$のとき、この不等式の解は存在しない。
$\boxed{\ \ ナ\ \ } \leqq a \leqq \boxed{\ \ ニ\ \ }$のとき、この不等式の解は
ある実数$p,q$によって$p \leqq x \leqq q$と表される。
$a \gt \boxed{\ \ ニ\ \ }$のときこの不等式の解は$\boxed{\ \ ヌ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
数学得意だよって天狗になっている中学生に解かせたい問題 ルートを外せ13

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{24n}$が整数となるような最小の整数nを求めよ。
大阪教育大学附属高等学校天王寺校舎
この動画を見る
$\sqrt{24n}$が整数となるような最小の整数nを求めよ。
大阪教育大学附属高等学校天王寺校舎
もっちゃんと数学

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left(\dfrac{5^{\sqrt3}}{25}\right)^{\sqrt{7+4\sqrt3}}$を計算せよ.
この動画を見る
$\left(\dfrac{5^{\sqrt3}}{25}\right)^{\sqrt{7+4\sqrt3}}$を計算せよ.
数学 高校入試 平方根の計算

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{30^4-20^4-10^4} =$
東北学院高等学校
この動画を見る
$\sqrt{30^4-20^4-10^4} =$
東北学院高等学校
6乗根をはずせ!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$6$乗根をはずせ.
$\sqrt[6]{99+70\sqrt2}$
この動画を見る
$6$乗根をはずせ.
$\sqrt[6]{99+70\sqrt2}$
複雑な平方根の計算

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(\sqrt 5 -2)^{100}(5+2 \sqrt 5)^{100}}{5^{50}}$
関西学院
この動画を見る
$\frac{(\sqrt 5 -2)^{100}(5+2 \sqrt 5)^{100}}{5^{50}}$
関西学院
18和歌山県教員採用試験(数学:4番 無理数の証明)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$2^x=5$をみたす実数$x$は
無理数であることを示せ.
この動画を見る
$\boxed{4}$
$2^x=5$をみたす実数$x$は
無理数であることを示せ.
福島大 基本対称式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
{$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=-4\\ab+bc+ca=7 \\
abc=10
\end{array}
\right.
\end{eqnarray}$
①$a^2+b^2+c^2$
②$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}$
③$\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}$
2021福島大過去問
この動画を見る
これを解け.
{$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=-4\\ab+bc+ca=7 \\
abc=10
\end{array}
\right.
\end{eqnarray}$
①$a^2+b^2+c^2$
②$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}$
③$\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}$
2021福島大過去問
息抜き雑問

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
①$\sqrt{3・5・17・257+1}$
どちらが大きいか?
②$9^{12}$ VS $127^{5}$
この動画を見る
これを解け.
①$\sqrt{3・5・17・257+1}$
どちらが大きいか?
②$9^{12}$ VS $127^{5}$
総復習
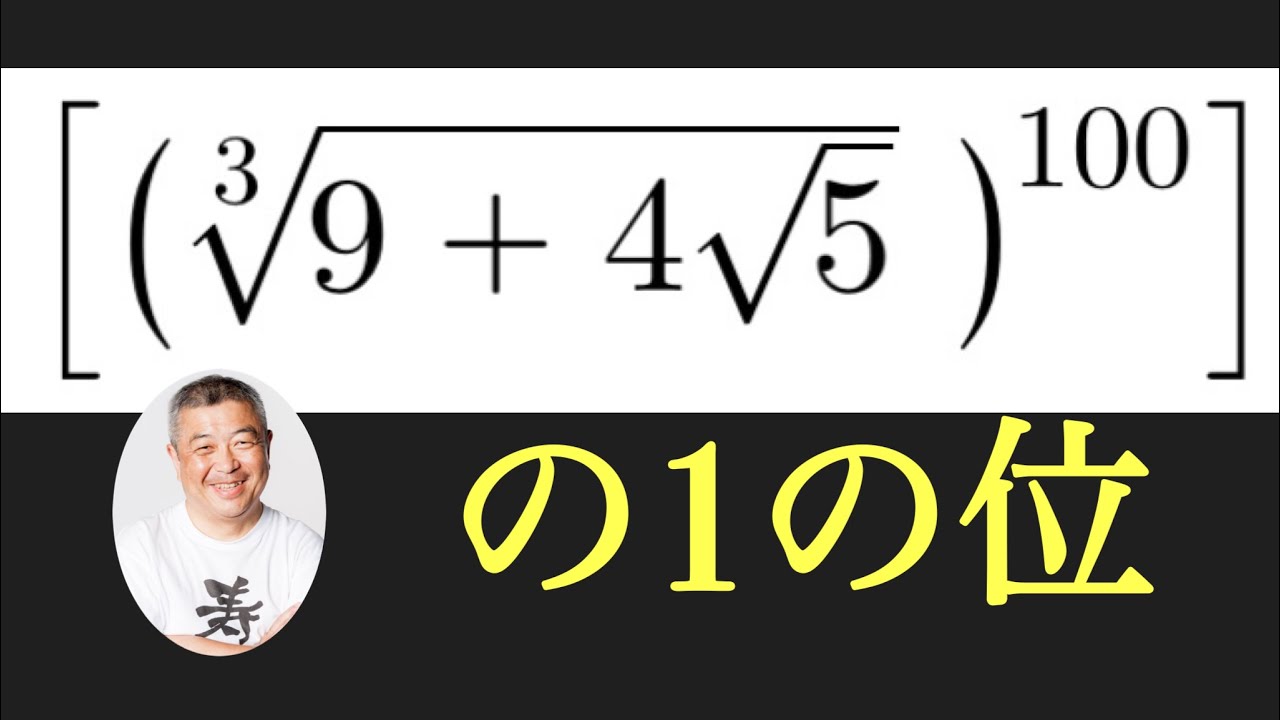
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$[(\sqrt[3]{9+4\sqrt5})^{100}]$の1の位を求めよ.
この動画を見る
$[(\sqrt[3]{9+4\sqrt5})^{100}]$の1の位を求めよ.
【中学数学】平方根・ルートの計算演習~乗法公式3~ 2-9.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})$
2⃣
$(5\sqrt{5}-2\sqrt{7})(5\sqrt{5}+2\sqrt{7})$
3⃣
$(\sqrt{3}+4)(\sqrt{3}-4)$
この動画を見る
1⃣
$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})$
2⃣
$(5\sqrt{5}-2\sqrt{7})(5\sqrt{5}+2\sqrt{7})$
3⃣
$(\sqrt{3}+4)(\sqrt{3}-4)$
ゆる言語学者バーゼル問題に驚く

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
バーゼル問題に関して解説していきます.
この動画を見る
バーゼル問題に関して解説していきます.
【中学数学】平方根・ルートの計算演習~乗法公式2~ 2-9.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(\sqrt{5}-\sqrt{2})^2$
2⃣
$(\sqrt{3}-5)^2$
3⃣
$(\sqrt{3}+3\sqrt{5})^2$
この動画を見る
1⃣
$(\sqrt{5}-\sqrt{2})^2$
2⃣
$(\sqrt{3}-5)^2$
3⃣
$(\sqrt{3}+3\sqrt{5})^2$
どっちがでかい?あれを証明します。

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$51^{100}$ VS $100!$
この動画を見る
どちらが大きいか?
$51^{100}$ VS $100!$
【中学数学】平方根・ルートの計算演習~乗法公式1~ 2-9【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(\sqrt{5}+3)(\sqrt{5}-2)$
2⃣
$(\sqrt{2}+3)(\sqrt{2}-1)$
3⃣
$(3\sqrt{5}-3)(6+3\sqrt{5})$
この動画を見る
1⃣
$(\sqrt{5}+3)(\sqrt{5}-2)$
2⃣
$(\sqrt{2}+3)(\sqrt{2}-1)$
3⃣
$(3\sqrt{5}-3)(6+3\sqrt{5})$
【中学数学】平方根・ルートの近似値の問題演習~解き方伝授~ 2-8【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt{2}=1.41,\sqrt{5}=2.23$として次の値を求めよ
(1)$\sqrt{200}$
(2)$\sqrt{0.02}$
(3)$\sqrt{0.2}$
この動画を見る
$\sqrt{2}=1.41,\sqrt{5}=2.23$として次の値を求めよ
(1)$\sqrt{200}$
(2)$\sqrt{0.02}$
(3)$\sqrt{0.2}$
平方根の計算 工夫せよ 久留米大附設

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$
久留米大附設高等学校
この動画を見る
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$
久留米大附設高等学校
【裏技】平方根・ルートの近似値の出し方~面白テクニック~

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
平方根・ルートの近似値の出し方紹介動画です
この動画を見る
平方根・ルートの近似値の出し方紹介動画です
6乗根 一橋の類題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\sqrt[6]{99+70\sqrt2}$
$\beta=\sqrt[6]{99-70\sqrt2}$
$Am=\alpha^{2n-1}-\beta^{2n-1}$
$n$が自然数のとき,$An$は整数であることを示せ.
この動画を見る
$\alpha=\sqrt[6]{99+70\sqrt2}$
$\beta=\sqrt[6]{99-70\sqrt2}$
$Am=\alpha^{2n-1}-\beta^{2n-1}$
$n$が自然数のとき,$An$は整数であることを示せ.
【中学数学】平方根・ルートの色々な計算~代入する問題~ 2-7【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$x=\sqrt{2}+1,y=\sqrt{2}-1$のとき、次の計算をしなさい
1⃣
$x^2-1$
2⃣
$x^2+2xy+y^2$
この動画を見る
$x=\sqrt{2}+1,y=\sqrt{2}-1$のとき、次の計算をしなさい
1⃣
$x^2-1$
2⃣
$x^2+2xy+y^2$
1の5乗根の計算
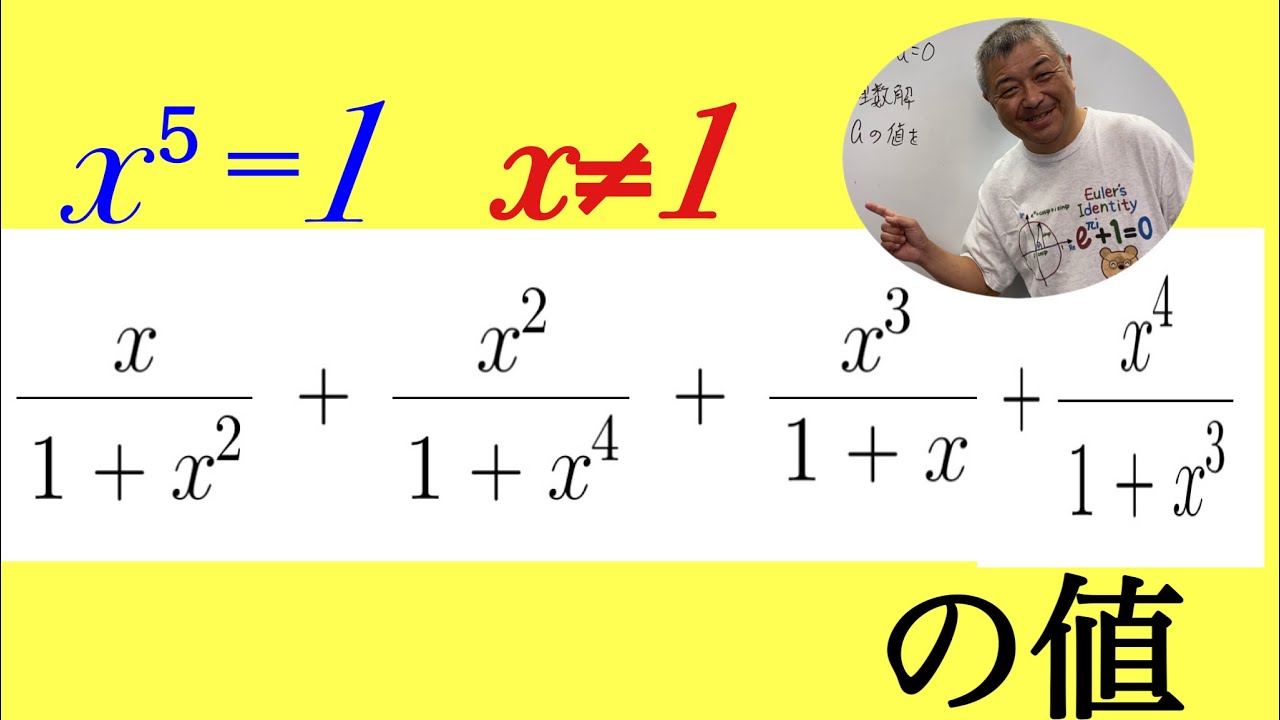
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^5=1,x \neq 1$である.
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.
この動画を見る
$x^5=1,x \neq 1$である.
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.
【中学数学】平方根・ルートの整数部分・小数部分を求める問題 2-6【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt{ 7 }$の整数部分と少数部分を求めよ
この動画を見る
$\sqrt{ 7 }$の整数部分と少数部分を求めよ
【数学Ⅰ/テスト対策】絶対値を含む方程式・不等式③

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の不等式を解け。
$|2x+1| \lt x+5$
この動画を見る
次の不等式を解け。
$|2x+1| \lt x+5$
【数学Ⅰ/テスト対策】絶対値を含む方程式・不等式①

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の方程式、不等式を解け。
(1)$|x+3|=2$
(2)$|3-x| \leqq 5$
(3)$|3x+2| \gt 7$
この動画を見る
次の方程式、不等式を解け。
(1)$|x+3|=2$
(2)$|3-x| \leqq 5$
(3)$|3x+2| \gt 7$
【中学数学】平方根・ルートの問題演習~計算の仕方~ 2-4.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$\sqrt{ 147 }-\sqrt{ 27 }-\sqrt{ 48 }$
2⃣
$\displaystyle \frac{2\sqrt{ 6 }}{3} \div \displaystyle \frac{4\sqrt{ 2 }}{3} \times \displaystyle \frac{7\sqrt{ 5 }}{2}$
この動画を見る
1⃣
$\sqrt{ 147 }-\sqrt{ 27 }-\sqrt{ 48 }$
2⃣
$\displaystyle \frac{2\sqrt{ 6 }}{3} \div \displaystyle \frac{4\sqrt{ 2 }}{3} \times \displaystyle \frac{7\sqrt{ 5 }}{2}$
灘高校の式の値 伝えたいこと、たくさん
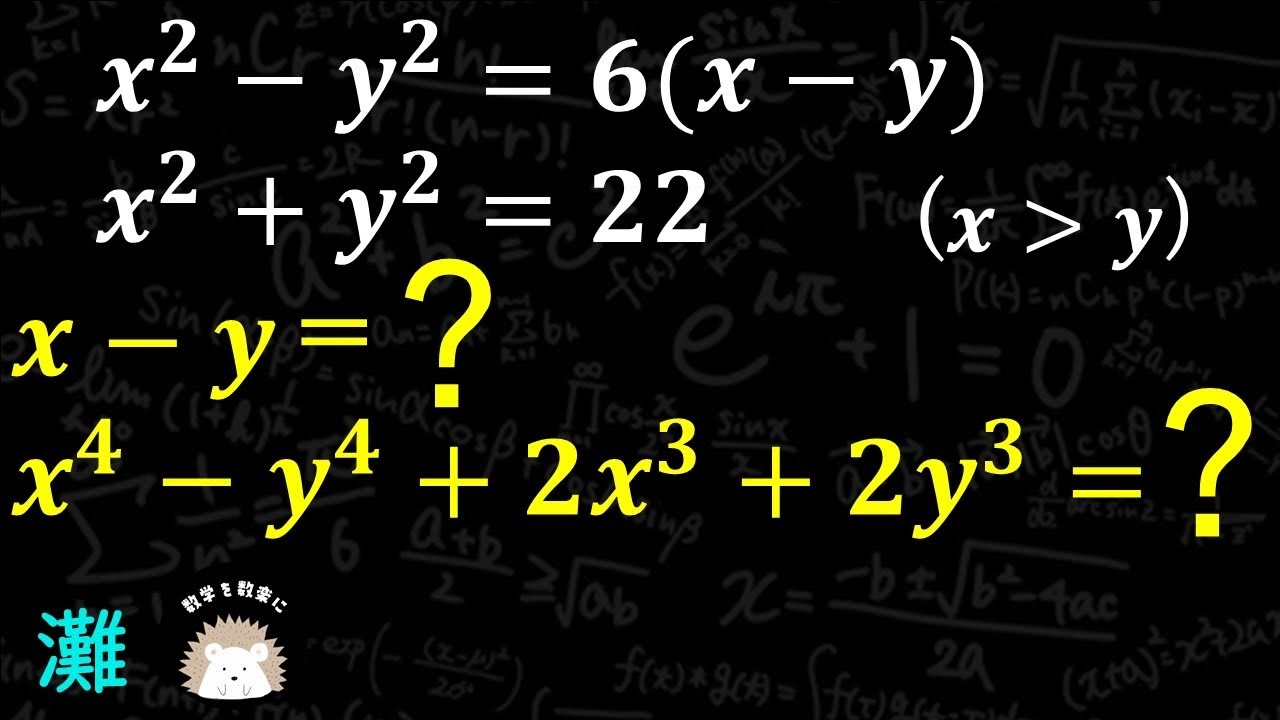
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
この動画を見る
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
【中学数学】平方根・ルートの足し算をどこよりも分かりやすく 2-4.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
この動画を見る
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
4の累乗の和で平方数を作れ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c,n$は自然数である.
$4^a+4^b+4^c=n^2$
$10\lt a\lt b\lt c$を満たす$(a,b,c)$を1組与えよ.
この動画を見る
$a,b,c,n$は自然数である.
$4^a+4^b+4^c=n^2$
$10\lt a\lt b\lt c$を満たす$(a,b,c)$を1組与えよ.
