 一次不等式(不等式・絶対値のある方程式・不等式)
一次不等式(不等式・絶対値のある方程式・不等式)
 一次不等式(不等式・絶対値のある方程式・不等式)
一次不等式(不等式・絶対値のある方程式・不等式)
【スムーズに!スマートに!】一次方程式:関西大倉高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.
関西大倉高校過去問
この動画を見る
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.
関西大倉高校過去問
式の値 早稲田実業

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
この動画を見る
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
絶対値を含む方程式
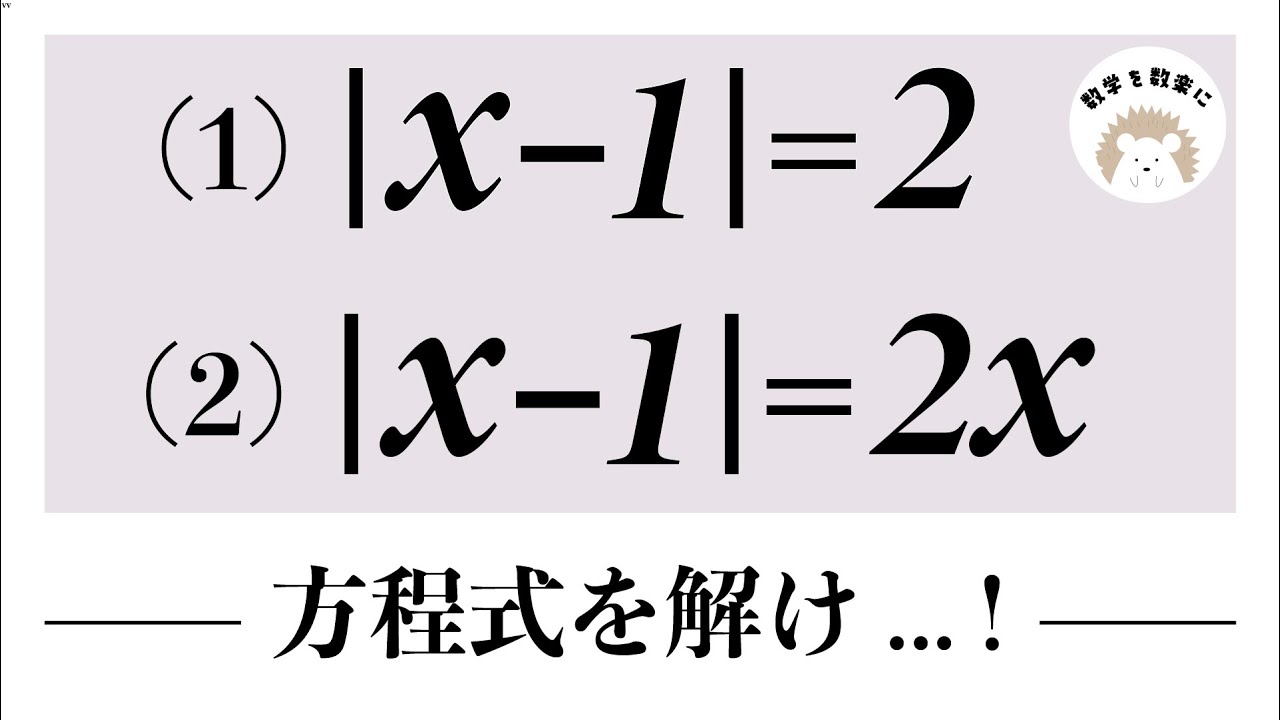
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
この動画を見る
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
対数と不等式

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
この動画を見る
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
神戸大 不等式の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
この動画を見る
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
数と式 1次不等式の利用【ホーン・フィールドがていねいに解説】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のものを求めよ。
(1)不等式$5(x-3)\lt -2(x-14)$を満たす最大の整数x
(2)不等式$\dfrac{x}{2}+\dfrac{4}{3}\geqq x-\dfrac{2}{3}$を満たす自然数xの個数
不等式$2x-3gt a+8x$について、次の問いに答えよ。
(1)解が$x\lt 1$となるように、定数aの値を定めよ。
(2)解が$x=0$を含むように、定数aの値の範囲を定めよ。
(3)この不等式を満たすxのうち、最大の整数が0となるように、定数aの値の範囲を定めよ。
aを定数とするとき、次の方程式、不等式を解け。
(1)$ax=1$
(2)$ax\leqq 2$
(3)$ax+6\gt 3x+2a$
この動画を見る
次のものを求めよ。
(1)不等式$5(x-3)\lt -2(x-14)$を満たす最大の整数x
(2)不等式$\dfrac{x}{2}+\dfrac{4}{3}\geqq x-\dfrac{2}{3}$を満たす自然数xの個数
不等式$2x-3gt a+8x$について、次の問いに答えよ。
(1)解が$x\lt 1$となるように、定数aの値を定めよ。
(2)解が$x=0$を含むように、定数aの値の範囲を定めよ。
(3)この不等式を満たすxのうち、最大の整数が0となるように、定数aの値の範囲を定めよ。
aを定数とするとき、次の方程式、不等式を解け。
(1)$ax=1$
(2)$ax\leqq 2$
(3)$ax+6\gt 3x+2a$
【奥が深い?スッキリ解答】一次関数:函館ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1次関数$ y=ax+3(a \lt 0)$
xの変域$ -2 \leqq x \leqq 5$であるとき,yの変域$ -2 \leqq y \leqq b $となるような
aとbの値を求めなさい.
函館ラサール高校過去問
この動画を見る
1次関数$ y=ax+3(a \lt 0)$
xの変域$ -2 \leqq x \leqq 5$であるとき,yの変域$ -2 \leqq y \leqq b $となるような
aとbの値を求めなさい.
函館ラサール高校過去問
神戸大 3次方程式の基本問題
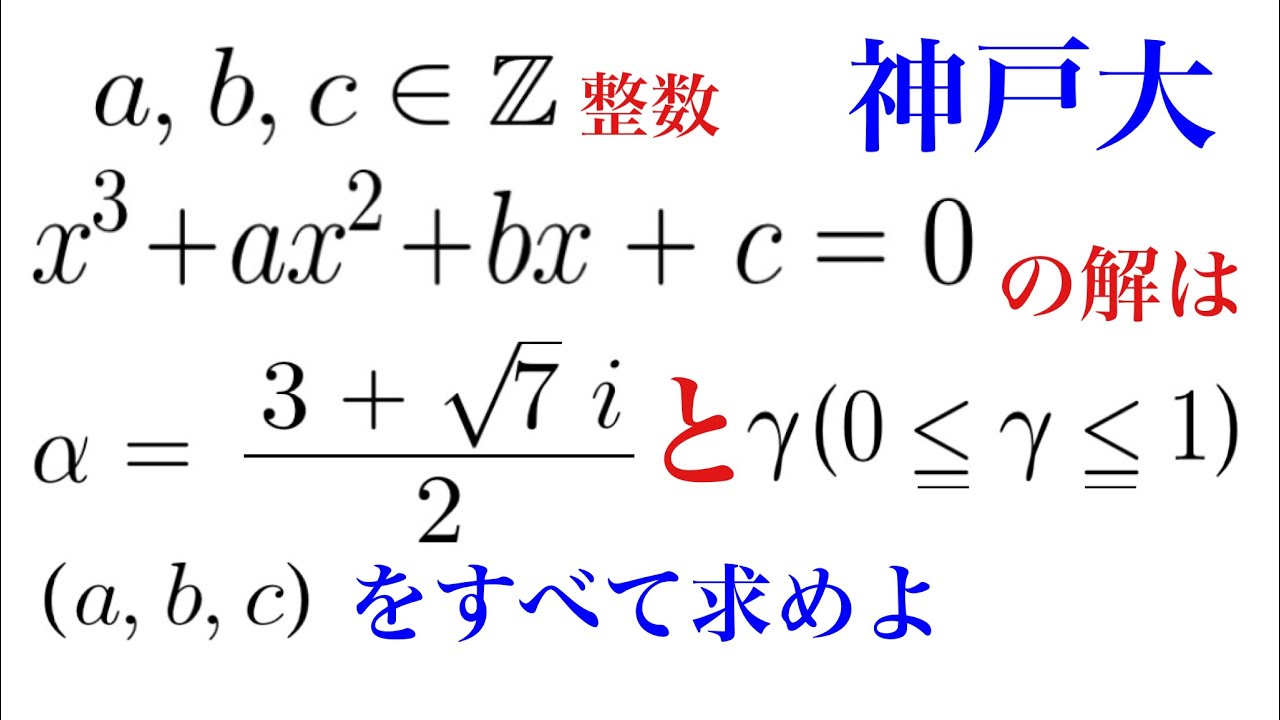
単元:
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#複素数平面#一次不等式(不等式・絶対値のある方程式・不等式)#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
この動画を見る
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
東大志望早坂の数学力チェック【大学受験プロジェクト】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
鈴木貫太郎先生が等式を満たすx+yの問題を解説します。
問題の解き方を学んで、参考にしましょう!
この動画を見る
鈴木貫太郎先生が等式を満たすx+yの問題を解説します。
問題の解き方を学んで、参考にしましょう!
根号を含んだ不等式の証明

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a>0,b>0$のとき
$3 \sqrt a + 2 \sqrt b > \sqrt {9a+4b}$
を示せ
この動画を見る
$a>0,b>0$のとき
$3 \sqrt a + 2 \sqrt b > \sqrt {9a+4b}$
を示せ
福田の数学〜慶應義塾大学2023年薬学部第1問(3)〜3次関数と絶対不等式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
知っていれば一瞬!絶対値の入った2次方程式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2 - 4|x| - 12 = 0$を解け
この動画を見る
$x^2 - 4|x| - 12 = 0$を解け
ルートと絶対値の入っている連立不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連立不等式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
(2 - \sqrt 5 )x > -1 \\
|3x-5| < 8
\end{array}
\right.
\end{eqnarray}
この動画を見る
連立不等式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
(2 - \sqrt 5 )x > -1 \\
|3x-5| < 8
\end{array}
\right.
\end{eqnarray}
x二乗をかけろ
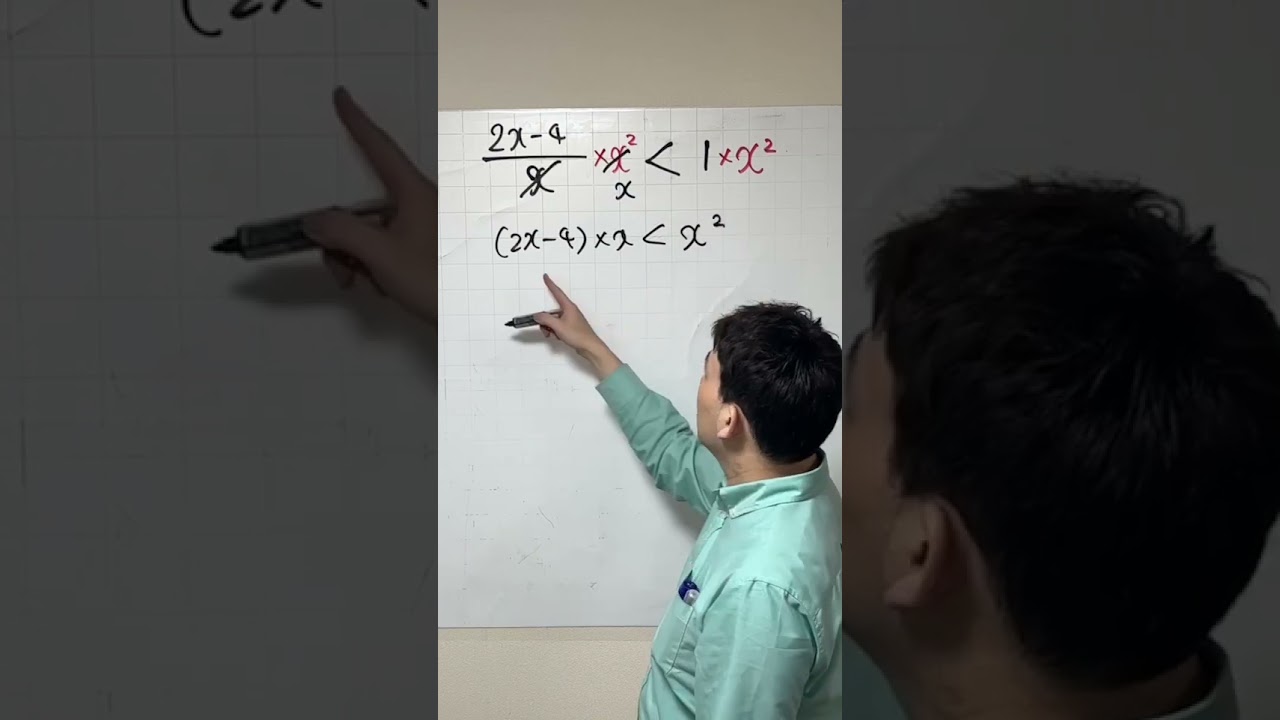
誰もが一度は間違える

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2x-4}{x} = 1$
$\frac{2x-4}{x} < 1$
この動画を見る
$\frac{2x-4}{x} = 1$
$\frac{2x-4}{x} < 1$
高等学校入学試験予想問題:鳥取県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#平面図形#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
この動画を見る
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
福田の1.5倍速演習〜合格する重要問題101〜慶應義塾大学2020年度環境情報学部第1問(1)〜不定方程式の解

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#平面上の曲線#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#加法定理とその応用#2次曲線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)正の実数xとyが9$x^2$+16$y^2$=144 を満たしているとき、xyの最大値は$\boxed{\ \ アイ\ \ }$である。
2020慶應義塾大学環境情報学部過去問
この動画を見る
$\Large\boxed{1}$ (1)正の実数xとyが9$x^2$+16$y^2$=144 を満たしているとき、xyの最大値は$\boxed{\ \ アイ\ \ }$である。
2020慶應義塾大学環境情報学部過去問
福田の数学〜2023年共通テスト速報〜数学IIB第1問三角関数と対数〜三角不等式と対数が有理数とならない条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
この動画を見る
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
福田の数学〜2023年共通テスト速報〜数学IA第1問不等式の解と図形の計量

単元:
#数Ⅰ#数と式#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第1問
[1]実数xについての不等式
|$x$+6| $\leqq$ 2
の解は
$\boxed{\ \ アイ\ \ } \leqq x \leqq \boxed{\ \ ウエ\ \ }$
である。
よって、実数$a,b,c,d$が
|(1-$\sqrt3$)($a-b$)($c-d$)+6| $\leqq$2
を満たしているとき、1-$\sqrt3$は負であることに注意すると、($a-b$)($c-d$)
の取り得る値の範囲は
$\boxed{\ \ オ\ \ }+\boxed{\ \ カ\ \ }\sqrt3 \leqq (a-b)(c-d) \leqq \boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3$
であることがわかる。
特に
$(a-b)(c-d)=\boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3 \cdots①$
であるとき、さらに
$(a-c)(b-d)=-3+\sqrt3 \cdots②$
が成り立つならば
$(a-d)(c-b)=\boxed{\ \ ケ\ \ }+\boxed{\ \ コ\ \ }\sqrt3 \cdots③$
であることが、等式①,②,③の左辺を展開して比較することによりわかる。
[2]
(1)点Oを中心とし、半径が5である円Oがある。この円周上に2点A,B
をAB=6となるようにとる。また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
(i)$\sin\angle ACB=\boxed{\boxed{\ \ サ\ \ }}$である。また、点Cを\angle ACBが鈍角となるようにとるとき、$\cos\angle ACB=\boxed{\boxed{\ \ シ\ \ }}$である。
(ii)点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直線ABに垂直な直線を引き、直線ABとの交点をDとするとき、
$\tan\angle OAD=\boxed{\boxed{\ \ ス\ \ }}$である。また、$\triangle ABC$の面積は$\boxed{\ \ セソ\ \ }$である。
$\boxed{\boxed{\ \ サ\ \ }}$ ~ $\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返し選んでもよい)
⓪$\displaystyle\frac{3}{5}$ ①$\displaystyle\frac{3}{4}$ ②$\displaystyle\frac{4}{5}$ ③ 1④$\displaystyle\frac{4}{3}$
⑤$-\displaystyle\frac{3}{5}$ ⑥$-\displaystyle\frac{3}{4}$ ⑦$-\displaystyle\frac{4}{5}$ ⑧ -1⑨$-\displaystyle\frac{4}{3}$
(2)半径が5である球Sがある。この球面上に3点P,Q,Rをとったとき、
これらの3点を通る平面α上でPQ=8, QR=5, RP=9であったとする。
球Sの球面上に点Tを三角錐TPQRの体積が最大となるようにとるとき、その体積を
求めよう。
まず、$\cos\angle QPR=\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}$である
ことから、$\triangle PQR$の面積は$\boxed{\ \ ツ\ \ }\sqrt{\boxed{\ \ テト\ \ }}$である。
次に、点Tから平面αに垂直な直線を引き、平面αとの交点をHとする。このとき、PH,QH,RHの長さについて、$\boxed{\boxed{\ \ ナ\ \ }}$が成り立つ。
以上より、三角錐TPQRの体積は$\boxed{\ \ ニヌ\ \ }\left(\sqrt{\boxed{\ \ ネノ\ \ }}+\sqrt{\boxed{\ \ ハ\ \ }}\right)$である。
$\boxed{\boxed{\ \ ナ\ \ }}$の解答群
⓪PH<QH<RH ①PH<RH<QH
②QH<PH<RH ③QH<RH<PH
④RH<PH<QH ⑤RH<QH<PH
⑥PH=QH=RH
2023共通テスト過去問
この動画を見る
第1問
[1]実数xについての不等式
|$x$+6| $\leqq$ 2
の解は
$\boxed{\ \ アイ\ \ } \leqq x \leqq \boxed{\ \ ウエ\ \ }$
である。
よって、実数$a,b,c,d$が
|(1-$\sqrt3$)($a-b$)($c-d$)+6| $\leqq$2
を満たしているとき、1-$\sqrt3$は負であることに注意すると、($a-b$)($c-d$)
の取り得る値の範囲は
$\boxed{\ \ オ\ \ }+\boxed{\ \ カ\ \ }\sqrt3 \leqq (a-b)(c-d) \leqq \boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3$
であることがわかる。
特に
$(a-b)(c-d)=\boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3 \cdots①$
であるとき、さらに
$(a-c)(b-d)=-3+\sqrt3 \cdots②$
が成り立つならば
$(a-d)(c-b)=\boxed{\ \ ケ\ \ }+\boxed{\ \ コ\ \ }\sqrt3 \cdots③$
であることが、等式①,②,③の左辺を展開して比較することによりわかる。
[2]
(1)点Oを中心とし、半径が5である円Oがある。この円周上に2点A,B
をAB=6となるようにとる。また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
(i)$\sin\angle ACB=\boxed{\boxed{\ \ サ\ \ }}$である。また、点Cを\angle ACBが鈍角となるようにとるとき、$\cos\angle ACB=\boxed{\boxed{\ \ シ\ \ }}$である。
(ii)点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直線ABに垂直な直線を引き、直線ABとの交点をDとするとき、
$\tan\angle OAD=\boxed{\boxed{\ \ ス\ \ }}$である。また、$\triangle ABC$の面積は$\boxed{\ \ セソ\ \ }$である。
$\boxed{\boxed{\ \ サ\ \ }}$ ~ $\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返し選んでもよい)
⓪$\displaystyle\frac{3}{5}$ ①$\displaystyle\frac{3}{4}$ ②$\displaystyle\frac{4}{5}$ ③ 1④$\displaystyle\frac{4}{3}$
⑤$-\displaystyle\frac{3}{5}$ ⑥$-\displaystyle\frac{3}{4}$ ⑦$-\displaystyle\frac{4}{5}$ ⑧ -1⑨$-\displaystyle\frac{4}{3}$
(2)半径が5である球Sがある。この球面上に3点P,Q,Rをとったとき、
これらの3点を通る平面α上でPQ=8, QR=5, RP=9であったとする。
球Sの球面上に点Tを三角錐TPQRの体積が最大となるようにとるとき、その体積を
求めよう。
まず、$\cos\angle QPR=\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}$である
ことから、$\triangle PQR$の面積は$\boxed{\ \ ツ\ \ }\sqrt{\boxed{\ \ テト\ \ }}$である。
次に、点Tから平面αに垂直な直線を引き、平面αとの交点をHとする。このとき、PH,QH,RHの長さについて、$\boxed{\boxed{\ \ ナ\ \ }}$が成り立つ。
以上より、三角錐TPQRの体積は$\boxed{\ \ ニヌ\ \ }\left(\sqrt{\boxed{\ \ ネノ\ \ }}+\sqrt{\boxed{\ \ ハ\ \ }}\right)$である。
$\boxed{\boxed{\ \ ナ\ \ }}$の解答群
⓪PH<QH<RH ①PH<RH<QH
②QH<PH<RH ③QH<RH<PH
④RH<PH<QH ⑤RH<QH<PH
⑥PH=QH=RH
2023共通テスト過去問
福田の1.5倍速演習〜合格する重要問題044〜北海道大学2017年度理系第1問〜不等式の証明と整数問題

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
自然数の2乗となる数を平方数という。
(1)自然数a,n,kに対して、
$n(n+1)+a=(n+k)^2$が成り立つとき、
$a \geqq k^2+2k-1$
が成り立つことを示せ。
(2)$n(n+1)+14$が平方数となるような自然数nを全て求めよ。
2017北海道大学理系過去問
この動画を見る
自然数の2乗となる数を平方数という。
(1)自然数a,n,kに対して、
$n(n+1)+a=(n+k)^2$が成り立つとき、
$a \geqq k^2+2k-1$
が成り立つことを示せ。
(2)$n(n+1)+14$が平方数となるような自然数nを全て求めよ。
2017北海道大学理系過去問
福田の1.5倍速演習〜合格する重要問題012〜京都大学2015年度文系数学第1問〜折れ線と交わらない条件

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次関数とグラフ#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$
のグラフとは交わらないような(p,q)の範囲を図示し、その面積を求めよ。
2015京都大学文系過去問
この動画を見る
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$
のグラフとは交わらないような(p,q)の範囲を図示し、その面積を求めよ。
2015京都大学文系過去問
福田の1.5倍速演習〜合格する重要問題007〜大阪大学2015年文系数学第1問〜不等式の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#三角関数#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数x,yが$|x| \leqq 1$と$|y| \leqq 1$を満たすとき、不等式
$0 \leqq x^2+y^2-2x^2y^2+2xy\sqrt{1-x^2}\sqrt{1-y^2} \leqq 1$
が成り立つことを示せ。
2015大阪大学文系過去問
この動画を見る
実数x,yが$|x| \leqq 1$と$|y| \leqq 1$を満たすとき、不等式
$0 \leqq x^2+y^2-2x^2y^2+2xy\sqrt{1-x^2}\sqrt{1-y^2} \leqq 1$
が成り立つことを示せ。
2015大阪大学文系過去問
以上未満の覚え方~とんとんと先生の教え方の違い~

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
以上未満の覚え方
この動画を見る
以上未満の覚え方
福田の数学〜立教大学2022年経済学部第1問(2)〜絶対の付いた方程式の解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$|X-|X-2||=1$の解をすべて求めよ
2022立教大学経済学部過去問
この動画を見る
$|X-|X-2||=1$の解をすべて求めよ
2022立教大学経済学部過去問
一度はみんな間違える変域 国分寺高校
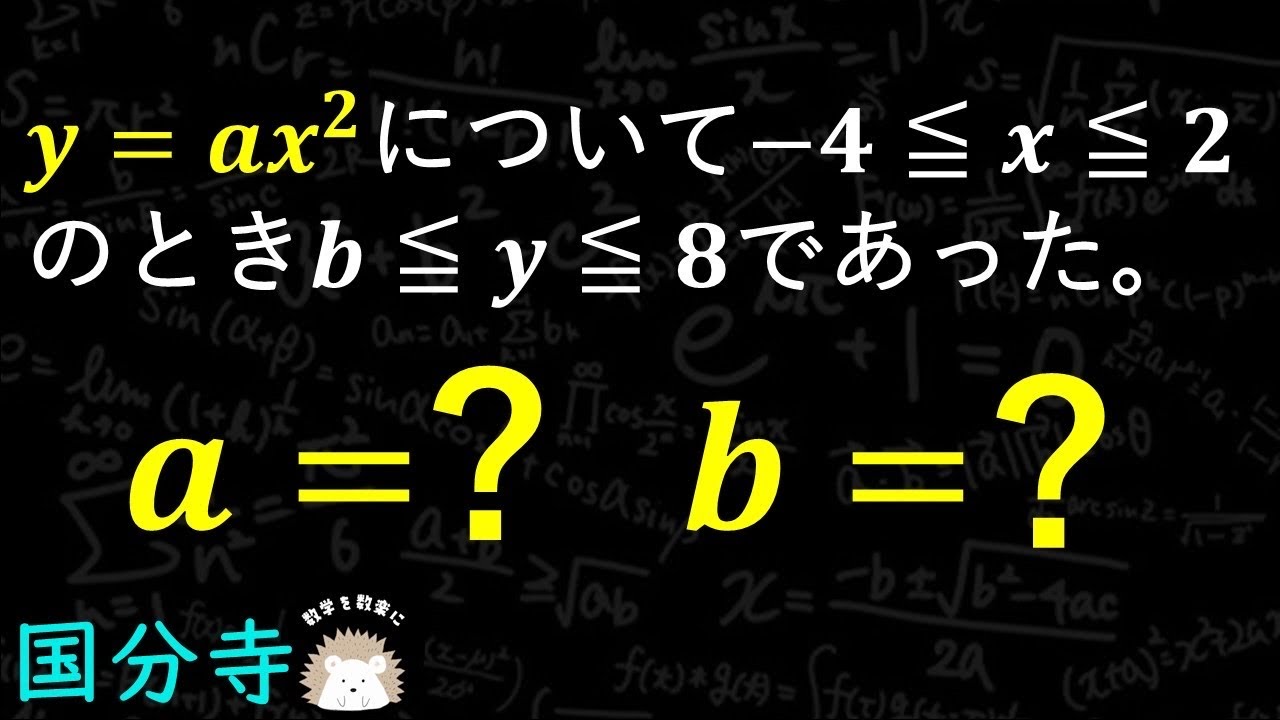
単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=ax^2$について$-4 \leqq x \leqq 2$のとき$b \leqq y \leqq 8$であった。
a=? b=?
国分寺高等学校
この動画を見る
$y=ax^2$について$-4 \leqq x \leqq 2$のとき$b \leqq y \leqq 8$であった。
a=? b=?
国分寺高等学校
【中学数学】不等式のつくり方~不等号の使い方~ 2-6【中1数学】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問. 次の数量の関係を表せ
(1) 1個x円の消しゴムを3個買ったら代金は300円だった
(2) s個のアメをt人に配ると、アメが足りない
(3) aからbを引いた時の差は3以上だ
(4) x円の鉛筆を定価の2割引きで買ったら代金はy円未満だった
(5) x kmの道のりを自転車に乗って、時速10 kmで走ったときかかった時間は3時間よりかかった
この動画を見る
問. 次の数量の関係を表せ
(1) 1個x円の消しゴムを3個買ったら代金は300円だった
(2) s個のアメをt人に配ると、アメが足りない
(3) aからbを引いた時の差は3以上だ
(4) x円の鉛筆を定価の2割引きで買ったら代金はy円未満だった
(5) x kmの道のりを自転車に乗って、時速10 kmで走ったときかかった時間は3時間よりかかった
式の値の範囲 仙台育英(宮城)
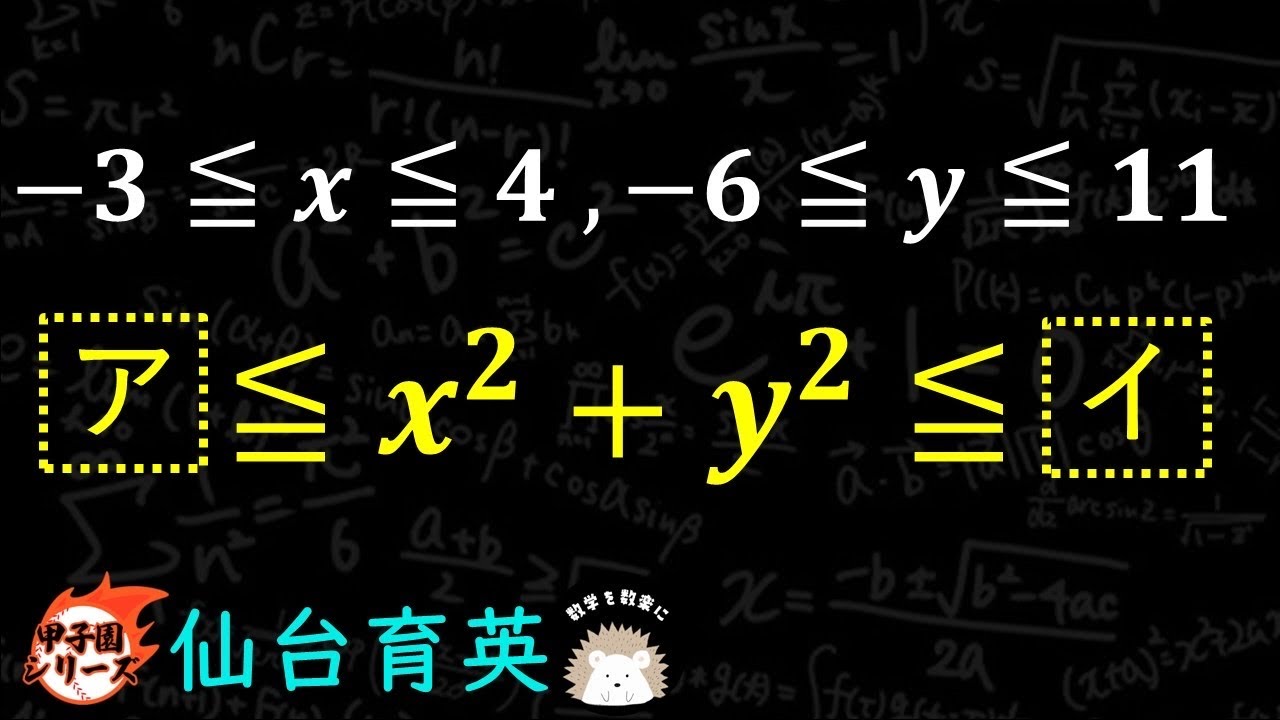
単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$-3 \leqq x \leqq 4$ , $-6 \leqq y \leqq 11$
$㋐ \leqq x^2 +y^2 \leqq ㋑$
仙台育英学園高等学校
この動画を見る
$-3 \leqq x \leqq 4$ , $-6 \leqq y \leqq 11$
$㋐ \leqq x^2 +y^2 \leqq ㋑$
仙台育英学園高等学校
ざ・一次不定方程式 合同式で楽々

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数x,yについて、$97x+83y=23$を満たす整数解x,yの一般解を求めよ.
この動画を見る
整数x,yについて、$97x+83y=23$を満たす整数解x,yの一般解を求めよ.
福田の数学〜慶應義塾大学2022年看護医療学部第2問(2)〜漸化式と和に関する不等式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
【保存版】絶対値の方程式の裏技

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
絶対値の方程式の裏技紹介動画です
この動画を見る
絶対値の方程式の裏技紹介動画です
