 数と式
数と式
 数と式
数と式
【迷わず進め!】二次方程式:東京都立八王子東高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#数と式#2次関数#2次方程式と2次不等式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ (x+1)^2+(x+1)(x+2)+4x+5=0 $を解け.
都立八王子東高校過去問
この動画を見る
2次方程式$ (x+1)^2+(x+1)(x+2)+4x+5=0 $を解け.
都立八王子東高校過去問
等式の変形だけど実は2次〇〇○
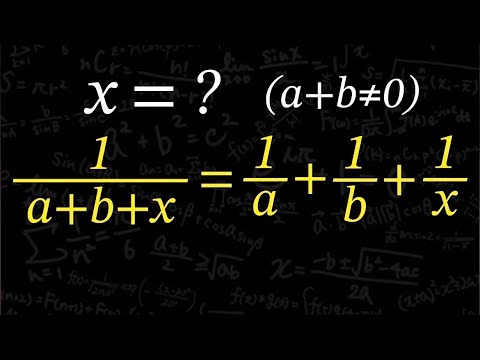
単元:
#数Ⅰ#数と式#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=?$ $(a+b \neq 0)$
$\frac{1}{a+b+x} = \frac{1}{a} + \frac{1}{b} + \frac{1}{x}$
この動画を見る
$x=?$ $(a+b \neq 0)$
$\frac{1}{a+b+x} = \frac{1}{a} + \frac{1}{b} + \frac{1}{x}$
【奥が深い?スッキリ解答】一次関数:函館ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1次関数$ y=ax+3(a \lt 0)$
xの変域$ -2 \leqq x \leqq 5$であるとき,yの変域$ -2 \leqq y \leqq b $となるような
aとbの値を求めなさい.
函館ラサール高校過去問
この動画を見る
1次関数$ y=ax+3(a \lt 0)$
xの変域$ -2 \leqq x \leqq 5$であるとき,yの変域$ -2 \leqq y \leqq b $となるような
aとbの値を求めなさい.
函館ラサール高校過去問
数と式 根号を含む計算【ホーン・フィールドがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\dfrac{\sqrt2}{\sqrt2-1}$の整数部分をa、小数部分をbとする。次の式の値を求めよ。
(1)$a$ (2)$b$ (3)$a+b+b^2$
次の各場合について、$\sqrt{x^2-10x+25}$をxの多項式で表せ。
(1)$x\geqq 5$ (2)$x\lt 5$
この動画を見る
$\dfrac{\sqrt2}{\sqrt2-1}$の整数部分をa、小数部分をbとする。次の式の値を求めよ。
(1)$a$ (2)$b$ (3)$a+b+b^2$
次の各場合について、$\sqrt{x^2-10x+25}$をxの多項式で表せ。
(1)$x\geqq 5$ (2)$x\lt 5$
因数分解

単元:
#数Ⅰ#数Ⅱ#数と式#式の計算(整式・展開・因数分解)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$9x^2+4168x+2^{15}$
この動画を見る
因数分解せよ.
$9x^2+4168x+2^{15}$
すべて○けろ!!式の値
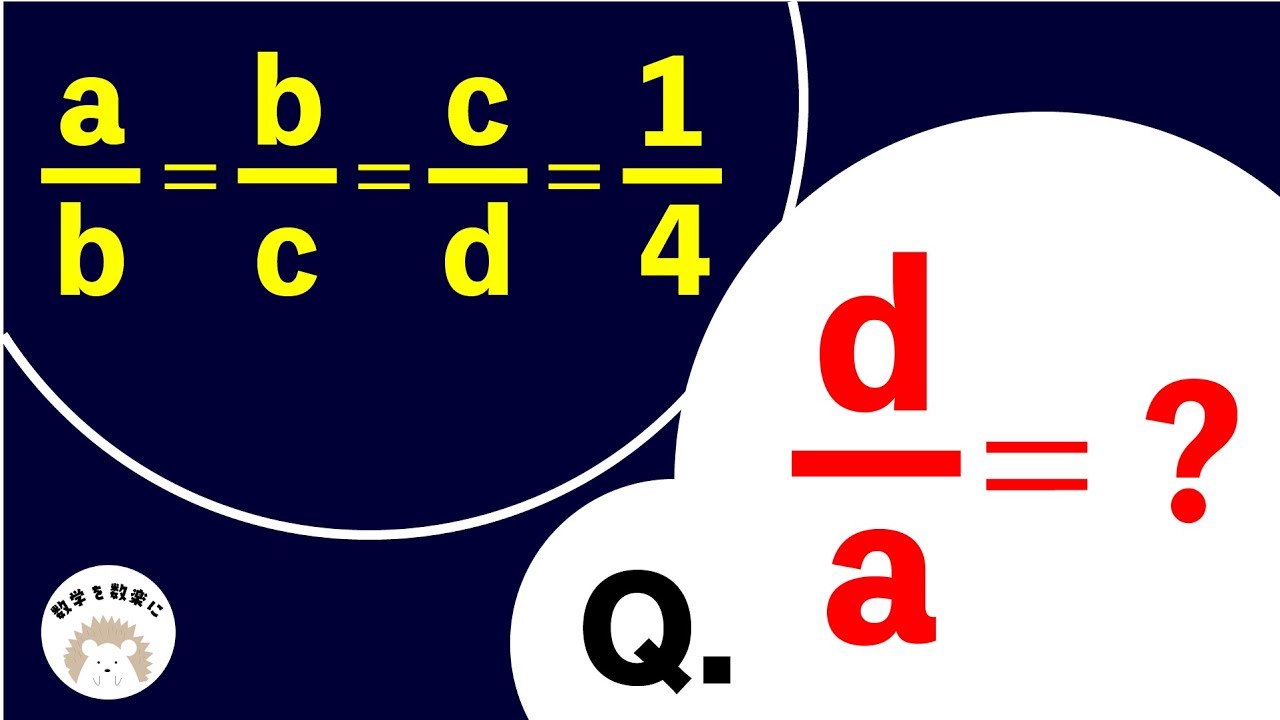
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{a}{b} = \frac{b}{c} = \frac{c}{d} = \frac{1}{4}$
$\frac{d}{a} =?$
この動画を見る
$\frac{a}{b} = \frac{b}{c} = \frac{c}{d} = \frac{1}{4}$
$\frac{d}{a} =?$
志木の展開
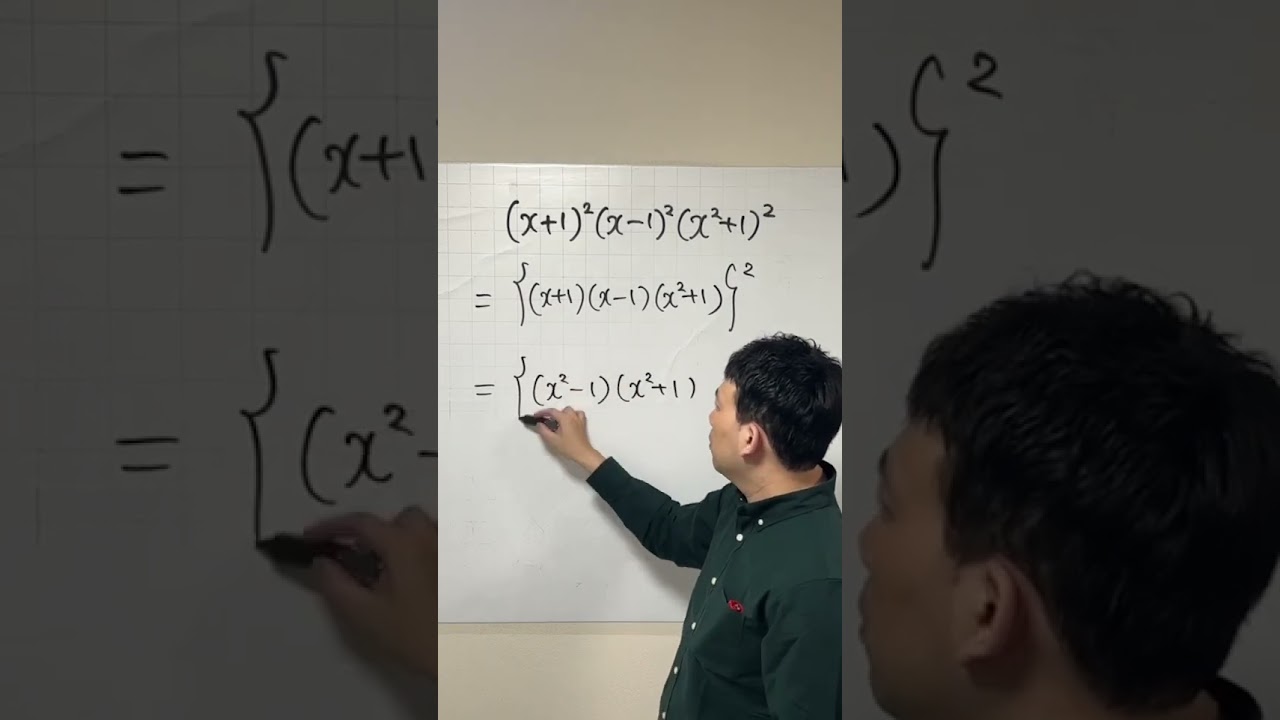
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
展開せよ
$(x+1)^2(x-1)^2(x^2+1)^2$
慶應義塾志木高等学校
この動画を見る
展開せよ
$(x+1)^2(x-1)^2(x^2+1)^2$
慶應義塾志木高等学校
ルートを外せ!!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
ルートを外せ
$\sqrt {3^2} = $
$\sqrt {\pi ^2} = $
$\sqrt {(\pi -3)^2} = $
$\sqrt {(3 - \pi )^2} = $
この動画を見る
ルートを外せ
$\sqrt {3^2} = $
$\sqrt {\pi ^2} = $
$\sqrt {(\pi -3)^2} = $
$\sqrt {(3 - \pi )^2} = $
めずらしい? √の計算 育英高校
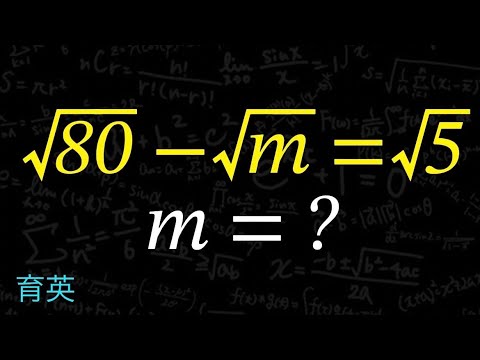
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{80} - \sqrt{m} = \sqrt{5}$
m=?
育英高等学校
この動画を見る
$\sqrt{80} - \sqrt{m} = \sqrt{5}$
m=?
育英高等学校
平方根の計算練習に、

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a \sqrt b$の形に直す
$\sqrt {27} = $
$\sqrt {45} = $
$\sqrt {54} = $
$\sqrt {63} = $
$\sqrt {90} = $
この動画を見る
$a \sqrt b$の形に直す
$\sqrt {27} = $
$\sqrt {45} = $
$\sqrt {54} = $
$\sqrt {63} = $
$\sqrt {90} = $
神戸大 3次方程式の基本問題
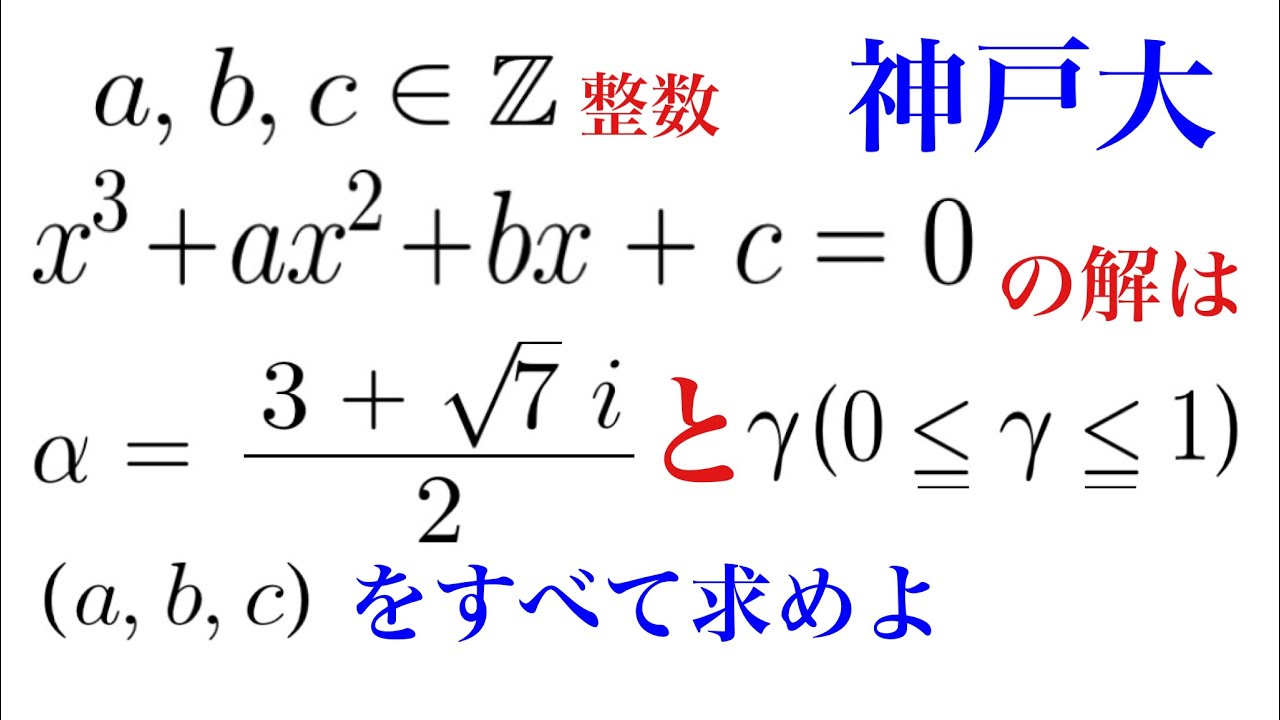
単元:
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#複素数平面#一次不等式(不等式・絶対値のある方程式・不等式)#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
この動画を見る
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
すべてを○けろ!!久留米大附設

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a,b,c,d,e$は正の数
$ab=1,bc=2,cd=3,de=4,ea=5$のとき
$a=?$
久留米大学付設高等学校
この動画を見る
$a,b,c,d,e$は正の数
$ab=1,bc=2,cd=3,de=4,ea=5$のとき
$a=?$
久留米大学付設高等学校
答えはあれじゃないよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^7=1,x \neq 1$のとき、
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x}+$
$\dfrac{x^5}{1+x^3}+\dfrac{x^6}{1+x^5}$の値を求めよ.
この動画を見る
$x^7=1,x \neq 1$のとき、
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x}+$
$\dfrac{x^5}{1+x^3}+\dfrac{x^6}{1+x^5}$の値を求めよ.
千葉大 整数解を持つ条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Pは素数であり,
$P^2+(5-P^2)x-3P=0$が整数解をもつのは$P=2$に限ることを示せ.
千葉大過去問
この動画を見る
Pは素数であり,
$P^2+(5-P^2)x-3P=0$が整数解をもつのは$P=2$に限ることを示せ.
千葉大過去問
平方根の複雑な計算を数楽に

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
指導講師:
数学を数楽に
問題文全文(内容文):
$(4 \sqrt2 + 4)(5 \sqrt 2 -5)^2$
この動画を見る
$(4 \sqrt2 + 4)(5 \sqrt 2 -5)^2$
解を出さなくても解ける! 難関高校受験するのなら絶対に知って欲しい 解と〇〇の関係 明大明治

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-4x+1=0$の2つの解をa,bとするとき
$a^{10}b^8 + a^6b^8 - 3a^5b^5 =?$
明治大学付属明治高等学校
この動画を見る
$x^2-4x+1=0$の2つの解をa,bとするとき
$a^{10}b^8 + a^6b^8 - 3a^5b^5 =?$
明治大学付属明治高等学校
地道に因数分解?一瞬で因数分解?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の式を因数分解せよ.
$(x-y)^3+(y-z)^3+(z-x)^3$
この動画を見る
次の式を因数分解せよ.
$(x-y)^3+(y-z)^3+(z-x)^3$
東大志望早坂の数学力チェック【大学受験プロジェクト】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
鈴木貫太郎先生が等式を満たすx+yの問題を解説します。
問題の解き方を学んで、参考にしましょう!
この動画を見る
鈴木貫太郎先生が等式を満たすx+yの問題を解説します。
問題の解き方を学んで、参考にしましょう!
中1生も高1生も大切な絶対値

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
絶対値が$\frac{13}{3}$以下である整数は何個?
神戸龍谷高等学校
この動画を見る
絶対値が$\frac{13}{3}$以下である整数は何個?
神戸龍谷高等学校
ナイスな連立三元2次方程式

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2-yz=1 \\\
y^2-zx=2\\\
z^2-xy=3
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2-yz=1 \\\
y^2-zx=2\\\
z^2-xy=3
\end{array}
\right.
\end{eqnarray}$
誘導にのれるか、のれないか。弘学館

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$45^2 = ?$
$x^2 - 2 \sqrt2x -2023 = 0$を解け
弘学館高等学校
この動画を見る
$45^2 = ?$
$x^2 - 2 \sqrt2x -2023 = 0$を解け
弘学館高等学校
ただの因数分解

三乗根の計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
${}^3 \sqrt 3 +{}^3 \sqrt {-3}$
この動画を見る
${}^3 \sqrt 3 +{}^3 \sqrt {-3}$
ただの因数分解と整数問題

単元:
#数Ⅰ#数A#数と式#場合の数と確率#式の計算(整式・展開・因数分解)#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①因数分解せよ.
$(x-2)(x-1)(x+1)(x+2)+2$
②$n^5-5n^3+5n+7$が120の倍数となる自然数nを一つ求めよ.
この動画を見る
①因数分解せよ.
$(x-2)(x-1)(x+1)(x+2)+2$
②$n^5-5n^3+5n+7$が120の倍数となる自然数nを一つ求めよ.
記数法になじもう!これを見ればあなたもバルタン星人になれる!
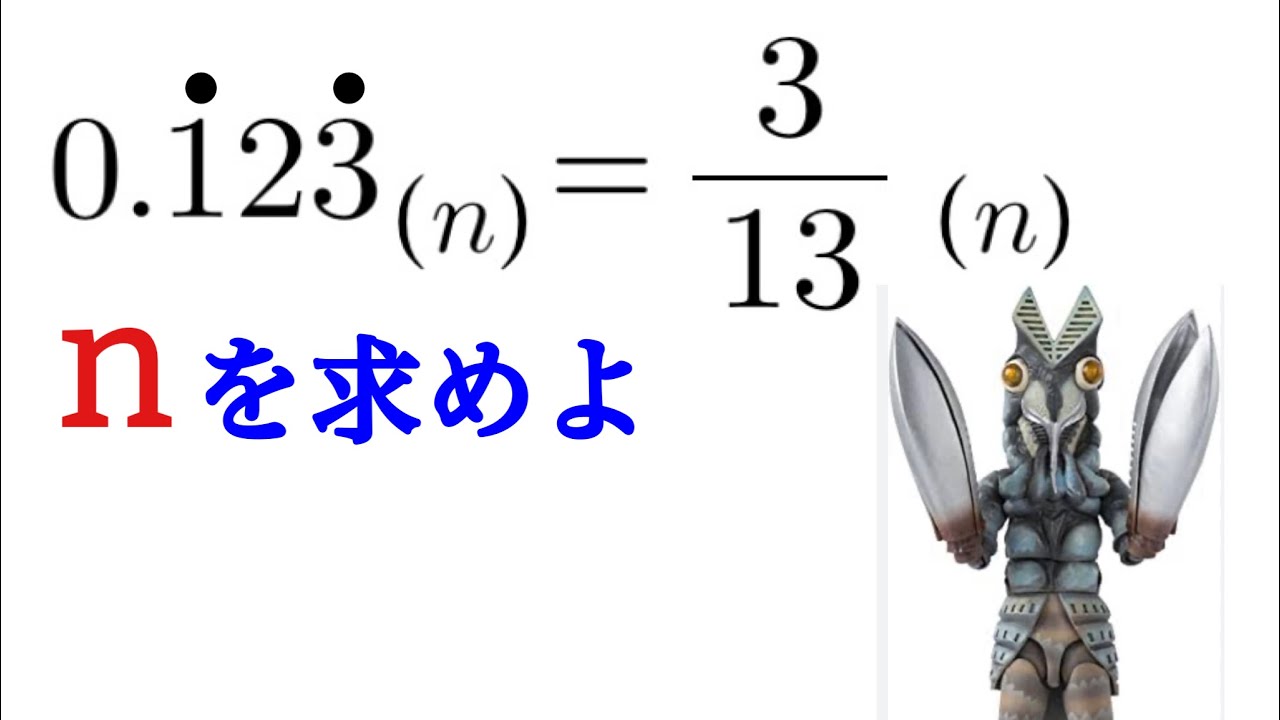
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$0.252525……=\dfrac{1}{3}$
$0.161616……=\dfrac{2}{11}$
$0.77777……?$
$0.123_{(n)}=\dfrac{3}{13}_{(n)}$
nを求めよ.
この動画を見る
$0.252525……=\dfrac{1}{3}$
$0.161616……=\dfrac{2}{11}$
$0.77777……?$
$0.123_{(n)}=\dfrac{3}{13}_{(n)}$
nを求めよ.
根号を含んだ不等式の証明

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a>0,b>0$のとき
$3 \sqrt a + 2 \sqrt b > \sqrt {9a+4b}$
を示せ
この動画を見る
$a>0,b>0$のとき
$3 \sqrt a + 2 \sqrt b > \sqrt {9a+4b}$
を示せ
真面目な数学の問題です。答えはスッキリ❗️

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$0.252525・・・・・・=\dfrac{1}{3}$
$0.161616・・・・・・=\dfrac{2}{11}$
$0.77777・・・・・・?$
この動画を見る
$0.252525・・・・・・=\dfrac{1}{3}$
$0.161616・・・・・・=\dfrac{2}{11}$
$0.77777・・・・・・?$
代入するときのちょっとした気遣い 安田女子

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt 2 = 1.414$ $\sqrt 3 = 1.732$
$\sqrt {0.12}=?$
安田女子高等学校
この動画を見る
$\sqrt 2 = 1.414$ $\sqrt 3 = 1.732$
$\sqrt {0.12}=?$
安田女子高等学校
気付けば一瞬だが、意外と難しいのよ。因数分解

福田の数学〜慶應義塾大学2023年薬学部第1問(3)〜3次関数と絶対不等式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
