 数と式
数と式
 数と式
数と式
05兵庫県教員採用試験(数学:1番 背理法)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$\log_2 3$が無理数であることを示せ.
この動画を見る
$\boxed{1}$
$\log_2 3$が無理数であることを示せ.
ただの因数分解 愛知医科大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$a^4+2a^3+3a^2+2a+1$
簡単に
$\sqrt{\dfrac{x^4+y^4+(x+y)^4}{2}}$
2019愛知医科大過去問
この動画を見る
因数分解せよ.
$a^4+2a^3+3a^2+2a+1$
簡単に
$\sqrt{\dfrac{x^4+y^4+(x+y)^4}{2}}$
2019愛知医科大過去問
ペアを作ろう!!A 大阪教育大学附属池田 洛南
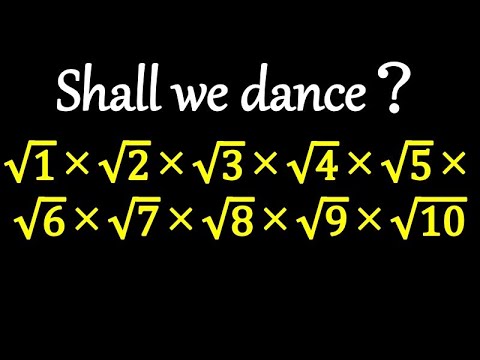
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{1} \times \sqrt{2} \times \sqrt{3} \times \sqrt{4} \times \sqrt{5} \times \sqrt{6} \times \sqrt{7} \times \sqrt{8} \times \sqrt{9} \times \sqrt{10} =$
大阪教育大学附属高等学校池田校舎
この動画を見る
$\sqrt{1} \times \sqrt{2} \times \sqrt{3} \times \sqrt{4} \times \sqrt{5} \times \sqrt{6} \times \sqrt{7} \times \sqrt{8} \times \sqrt{9} \times \sqrt{10} =$
大阪教育大学附属高等学校池田校舎
高校範囲の因数分解

√6…
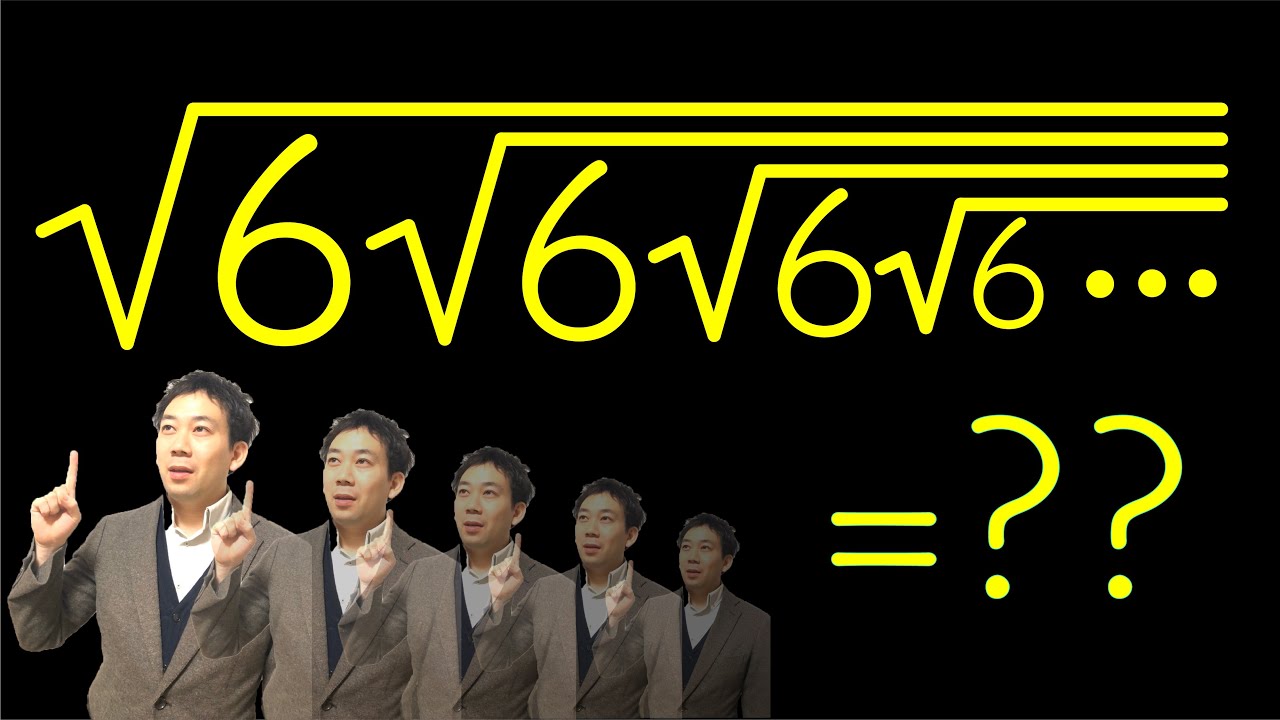
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{6\sqrt{6\sqrt{6 \cdots}}}$
この動画を見る
$\sqrt{6\sqrt{6\sqrt{6 \cdots}}}$
【数Ⅰ】中高一貫校用問題集(論理・確率編)集合と命題:命題と条件:必要条件、十分条件の見分け方

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$「x=2」$ならば$「x^2=2x」$であるための○○条件を求めよ.
この動画を見る
$「x=2」$ならば$「x^2=2x」$であるための○○条件を求めよ.
【数Ⅰ】中高一貫校用問題集(論理・確率編)集合と命題:命題と条件:範囲を利用した真偽の見分け方

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の命題の真偽を調べよ
$「-1<x<2」 ⇒ 「x>-2」$
この動画を見る
次の命題の真偽を調べよ
$「-1<x<2」 ⇒ 「x>-2」$
【数Ⅰ】中高一貫校問題集3(論理・確率編)17:集合と命題:命題と条件:範囲を利用した真偽の見分け方

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の命題の真偽を調べよ
「-1<x<2」 ⇒ 「x>-2」【集合と命題】
この動画を見る
次の命題の真偽を調べよ
「-1<x<2」 ⇒ 「x>-2」【集合と命題】
【数Ⅰ】中高一貫校問題集3(論理・確率編)19:集合と命題:命題と条件:必要条件、十分条件の見分け方

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
「x=2」ならば「x²=2x」であるための○○条件である 【集合と命題】【必要十分条件】
この動画を見る
「x=2」ならば「x²=2x」であるための○○条件である 【集合と命題】【必要十分条件】
新高1生へ 失敗しないたすきがけ因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$48x^2+5x-18$
$(ax+b)(cx+d)$
この動画を見る
因数分解せよ.
$48x^2+5x-18$
$(ax+b)(cx+d)$
【知らなきゃ損!!】因数分解の応用例。これすぐ解けますか?【高校数学】

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
以下を因数分解してください
$(2x-1)^2-(2x-1)-2$
この動画を見る
以下を因数分解してください
$(2x-1)^2-(2x-1)-2$
たすきがけは、もう焦らない。これ見たらカンペキです【高校数学】

サルでも分かる3次の因数分解。これ見たらカンペキ?!【高校数学】

数学「大学入試良問集」【1−3 背理法・対偶】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
(ⅰ)$\sqrt{ 2 }$が無理数であることを証明せよ。
(ⅱ)実数$a$が$a^3+\alpha+1=0$を満たすとき、$\alpha$が無理数であることを証明せよ。
(2)
(ⅰ)$n$を自然数とするとき、$n^3$が$3$の倍数ならば、$n$は$3$の倍数のなることを証明せよ。
(ⅱ)$\sqrt[ 3 ]{ 3 }$が無理数であることを証明せよ。
この動画を見る
次の問いに答えよ。
(1)
(ⅰ)$\sqrt{ 2 }$が無理数であることを証明せよ。
(ⅱ)実数$a$が$a^3+\alpha+1=0$を満たすとき、$\alpha$が無理数であることを証明せよ。
(2)
(ⅰ)$n$を自然数とするとき、$n^3$が$3$の倍数ならば、$n$は$3$の倍数のなることを証明せよ。
(ⅱ)$\sqrt[ 3 ]{ 3 }$が無理数であることを証明せよ。
数学「大学入試良問集」【1−2 数と式】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$x,y$を実数とする。
下の(1)、(2)の文中の□にあてはまるものを、次の(ア)、(イ)、(ウ)、(エ)の中から選べ。
(ア)必要条件ではあるが、十分条件ではない
(イ)十分条件ではあるが、必要条件ではない
(ウ)必要十分条件である
(エ)必要条件でも、十分条件でもない
(1)$x^2+y^2 \lt 1$は、$-1 \lt x \lt $であるための□。
(2)$-1 \lt x \lt 1$かつ$-1 \lt y \lt 1$は$x^2+y^2 \lt 1$であるための□。
この動画を見る
$x,y$を実数とする。
下の(1)、(2)の文中の□にあてはまるものを、次の(ア)、(イ)、(ウ)、(エ)の中から選べ。
(ア)必要条件ではあるが、十分条件ではない
(イ)十分条件ではあるが、必要条件ではない
(ウ)必要十分条件である
(エ)必要条件でも、十分条件でもない
(1)$x^2+y^2 \lt 1$は、$-1 \lt x \lt $であるための□。
(2)$-1 \lt x \lt 1$かつ$-1 \lt y \lt 1$は$x^2+y^2 \lt 1$であるための□。
【できなきゃ死 Part2】今のうちに展開をマスターしとこ【数学】【高校数学】
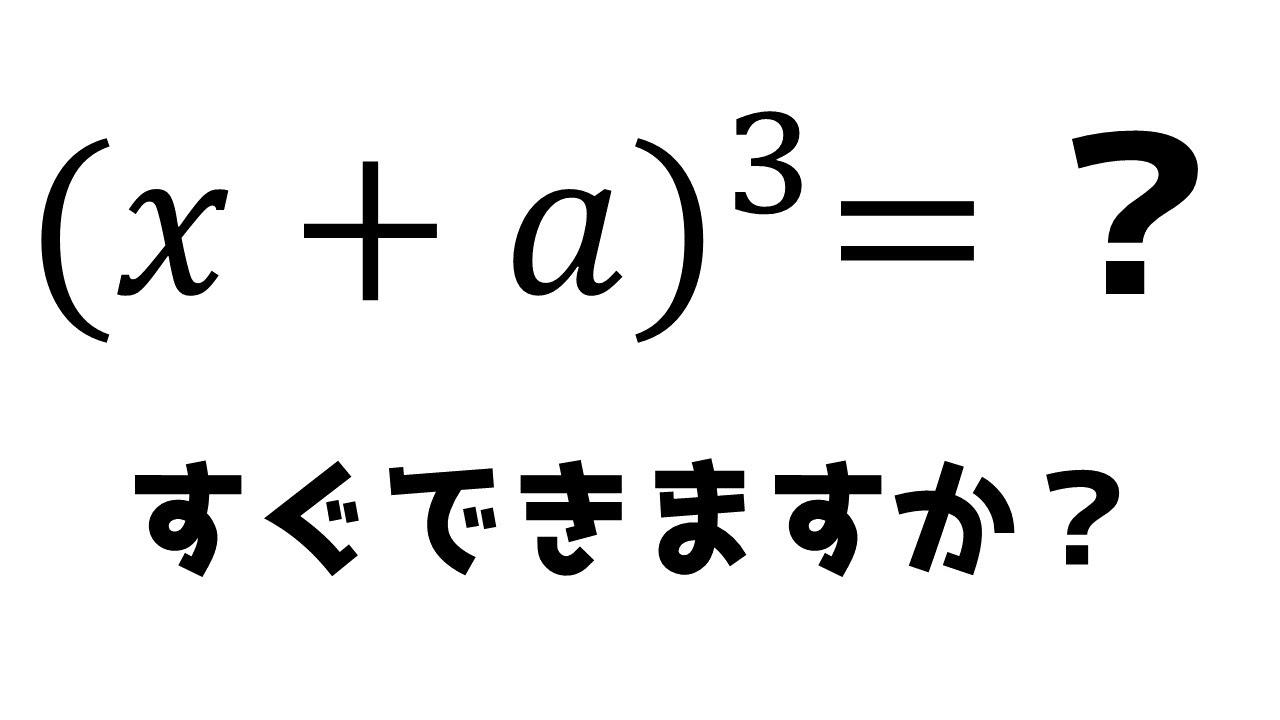
【できなきゃ死】今のうちに展開をマスターしとこ【数学】【中学3年数学、高校数学】
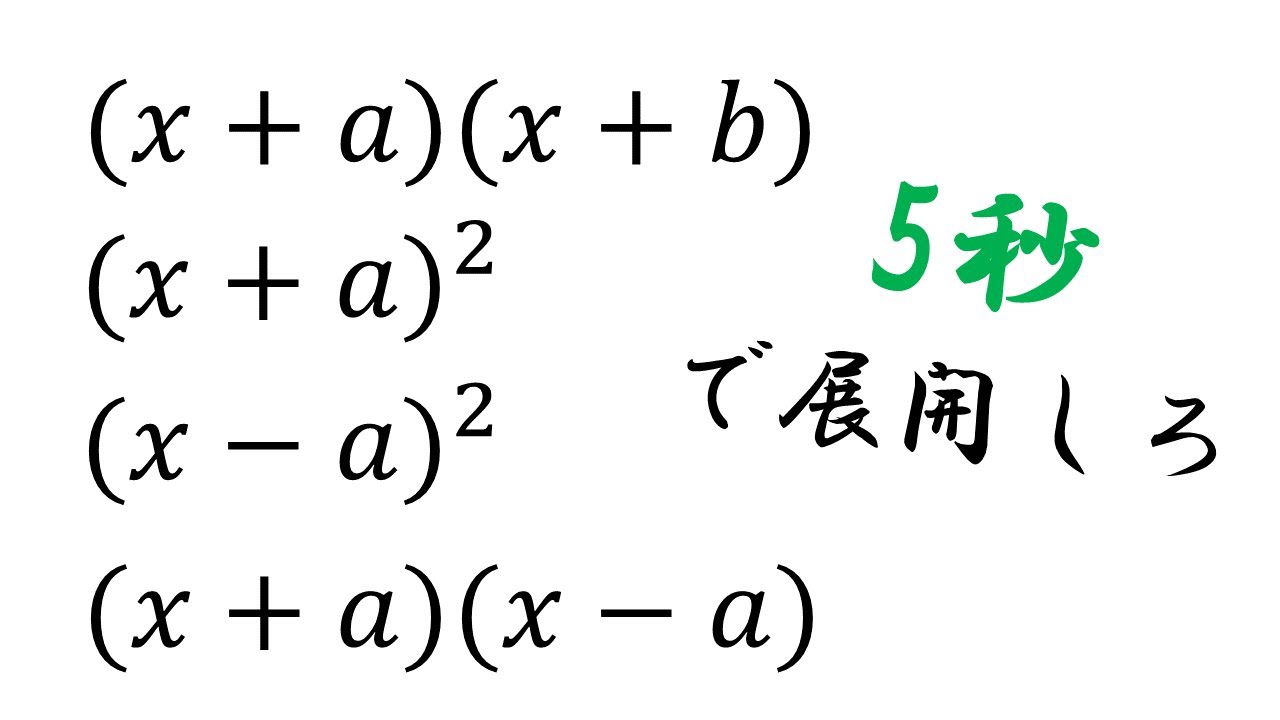
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
①$(x+a)(x+b)=$
②$(x+a)^2=$
③$(x-a)^2=$
④$(x+a)(x-a)=$
この動画を見る
①$(x+a)(x+b)=$
②$(x+a)^2=$
③$(x-a)^2=$
④$(x+a)(x-a)=$
【みんな大好き】因数分解:明治薬科~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治薬科
$x^2+4xy+3y^2+2x+4y+1$
因数分解せよ。
この動画を見る
入試問題 明治薬科
$x^2+4xy+3y^2+2x+4y+1$
因数分解せよ。
因数分解&ご報告

ただの因数分解2021関西医科大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$(x^2-15x-2)(x^2+15x-2)-5x^2+2021$
2021関西医科大過去問
この動画を見る
因数分解せよ.
$(x^2-15x-2)(x^2+15x-2)-5x^2+2021$
2021関西医科大過去問
ルートを外せ11 B 2021 中央大附属

単元:
#数学(中学生)#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{60(n+1)(n^2-1)}$が整数となるような2ケタの整数nをすべて求めよ。
2021中央大学附属高等学校
この動画を見る
$\sqrt{60(n+1)(n^2-1)}$が整数となるような2ケタの整数nをすべて求めよ。
2021中央大学附属高等学校
そのまま〇〇するな! A A

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=-3x^2$でxの変域が$-4 \leqq x \leqq 1$のとき
$▢ \leqq y \leqq ▢$
2021東京都立共通問題
この動画を見る
$y=-3x^2$でxの変域が$-4 \leqq x \leqq 1$のとき
$▢ \leqq y \leqq ▢$
2021東京都立共通問題
2021 八王子東高校最初の一問 A

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{\sqrt 6 + 2}{\sqrt 2})(\frac{\sqrt 2 - \sqrt 3 }{3})$
2021八王子東高等学校
この動画を見る
$(\frac{\sqrt 6 + 2}{\sqrt 2})(\frac{\sqrt 2 - \sqrt 3 }{3})$
2021八王子東高等学校
○か✖️か 2021 中大横浜 B

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正しいものをすべて選べ
(ア)$\frac{-4+2\sqrt 3}{2} = -2+2\sqrt 3$
(イ)1は素数である
(ウ)$\sqrt{1.69}$は有理数
(エ)$\frac{3}{0}=0$である
(オ)$\sqrt 9 + \sqrt{16} = \sqrt{25}$
2021中央大学附属横浜高等学校
この動画を見る
正しいものをすべて選べ
(ア)$\frac{-4+2\sqrt 3}{2} = -2+2\sqrt 3$
(イ)1は素数である
(ウ)$\sqrt{1.69}$は有理数
(エ)$\frac{3}{0}=0$である
(オ)$\sqrt 9 + \sqrt{16} = \sqrt{25}$
2021中央大学附属横浜高等学校
慶応高校 一言言いたいだけの動画

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$(a^2-2a-6)(a^2-2a-17)+18$
2021慶應義塾高過去問
この動画を見る
因数分解せよ.
$(a^2-2a-6)(a^2-2a-17)+18$
2021慶應義塾高過去問
三乗根を外せ (類題)学習院大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
三乗根を外せ.
$\sqrt[3]{9-4\sqrt5}$
この動画を見る
三乗根を外せ.
$\sqrt[3]{9-4\sqrt5}$
2021 灘高校 最初の一問

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(2\sqrt 2 -3)^2=$
$\sqrt{\sqrt{(10-7\sqrt 2)^2} - \sqrt{(7-5\sqrt 2)^2} }$
2021灘高等学校
この動画を見る
$(2\sqrt 2 -3)^2=$
$\sqrt{\sqrt{(10-7\sqrt 2)^2} - \sqrt{(7-5\sqrt 2)^2} }$
2021灘高等学校
【最速】和積公式/積和公式を5分でマスター

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
和積公式/積和公式の解説動画です
-----------------
①$\sin A +\sin B$
②$\sin A -\sin B$
③$\cos A +\cos B$
④$\cos A +\cos B$
この動画を見る
和積公式/積和公式の解説動画です
-----------------
①$\sin A +\sin B$
②$\sin A -\sin B$
③$\cos A +\cos B$
④$\cos A +\cos B$
【数Ⅰ】数と式:繁分数② 次の式を簡単にしよう。x³/{x-1/(x+1/x)}

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を簡単にしよう。
$\dfrac{x^3}{x-\dfrac{1}{x+\dfrac{1}{x}}}$
この動画を見る
次の式を簡単にしよう。
$\dfrac{x^3}{x-\dfrac{1}{x+\dfrac{1}{x}}}$
2021昭和(医)いわくつき学習院の過去問と同じ!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(\sqrt{n^2-9n+19})^{n^2+5n-14}=1$を満たす自然数$n$をすべて求めよ.
2021昭和(医)
この動画を見る
$(\sqrt{n^2-9n+19})^{n^2+5n-14}=1$を満たす自然数$n$をすべて求めよ.
2021昭和(医)
