問題文全文(内容文)：
2次関数の値の範囲と最大値・最小値
①$y=x^2-2x+1$を定義域(0 \leqq x \leqq 3)でグラフをかけ

②$y=2x^2-4x+1$について$-1 \leq z \leq 2$の範囲での最大値と最小値を求めよ

③$y=-3x^2-4x-1$について$1 \leq z \leq 3$の範囲での最大値と最小値を求めよ

問題文全文(内容文)：
数学$\textrm{I}$　2次方程式の解の分離
$x^2-2ax+a+2=0$
の解が$1 \lt x \lt 3$の範囲に少なくとも
1つ存在する$a$の範囲を求めよ。

問題文全文(内容文)：
①
1.以下の文字式を[]内の文字について降べきの順に整理しなさい
　（1）$a^3+a^2+a+4a^4+6a^6-3a^4$　[a]
　（2）$x^2+2y^2+z^2-xy+yz+zx$　[z]

2.$A=x^2-ax+1,B=a^2+3ax+2$のとき$A-${$3B+(A-B)$}を計算しなさい。


②
1.次の式を計算しなさい
　$(-2ab^3)^3$

2.次の式を展開しなさい
　（1）$(a-3b)^2$
　（2）$(2+3a)(2-3a)$
　（3）$(a+5)(a-6)$

3.次の式を展開しなさい
　（1）$(x^2+2x+1)^2$
　（2）$(4a^2+9)(2a-3)(2a+3)$


③
1.次の式を因数分解しなさい
　（1）$2a^2x-4ab$
　（2）$x^2+6x+9$
　（3）$x^2-5x+6$
　（4）$16a^2-9b^2$

2.次の式を因数分解しなさい
　（1）$x^2+x+\displaystyle \frac{1}{4}$
　（2）$4x^2-16$


④
1.次の式を因数分解しなさい
　（1）$2x^2-5x-3$
　（2）$9x^2+3ab-2b^2$
　（3）$3x^2-11ab-4b^2$
　（4）$8x^2-14xy-15y^2$

2.次の式を因数分解しなさい
　（1）$4a^2-b^2-2bc-c^2$
　（2）$(x+y+1)(x+y+3)-15$
　（3）$2x^2-2y^2+3xy+x+2y$
　（4）$(x+y)^2-4(x+y)+4$


⑤
1.次の式を展開しなさい
　（1）$(2x-1)^3$
　（2）$(2x+3)(4x^2+6x+9)$

2.次の式を因数分解しなさい
　（1）$1-8a^3$
　（2）$216x^3+125y^3$


⑥
1.次の循環小数を分数で表せ
　（1）$0.\dot{ 9 }$
　（2）$0.\dot{ 8 }\dot{ 3 }$


⑦
1.次の値を求めなさい
　（1）$|\sqrt{ 3 }-\sqrt{ 5 }|$
　（2）$|1|-|-2|$
　（3）$|\sqrt{ 2 }+\sqrt{ 3 }||\sqrt{ 2 }-\sqrt{ 3 }|$

2.次の値を求めなさい
　（1）$\sqrt{ 32 }+\sqrt{ 128 }$
　（2）$(2+\sqrt{ 2 })^2$
　（3）$\sqrt{ 3+2\sqrt{ 2 } }$


⑧
1.次の式を簡単にしなさい
　（1）$\displaystyle \frac{2}{\sqrt{ 5 }}$

　（2）$\displaystyle \frac{1+\sqrt{ 6 }}{\sqrt{ 3 }}$

　（3）$\displaystyle \frac{2-\sqrt{ 2 }}{2+\sqrt{ 2 }}$


2.$2\sqrt{ 2 }$の整数部分を$a$,小数部分を$b$とするとき、次の式の値を求めなさい
　（1）$a$
　（2）$b$
　（3）$\displaystyle \frac{a}{b}$


⑨
1.$x=\displaystyle \frac{2-\sqrt{ 2 }}{2+\sqrt{ 2 }},y=\displaystyle \frac{2+\sqrt{ 2 }}{2-\sqrt{ 2 }}$のとき、次の式の値を求めなさい
　（1）$x+y,xy$
　（2）$x^2+y^2$
　（3）$x^3+y^3$


⑩
1.$a \gt b$のとき、次の□にあてはまる不等号を入れなさい。
　（1）$-2a+5□-2b+5$
　（2）$3a□3b$


2.次の不等式を解きなさい
　（1）$5x+6 \lt 11$
　（2）$-6x+1 \geqq 19$
　（3）$3(2x+1) \gt -(4x+5)+2$


⑪
1.次の連立不等式を解きなさい
　（1）$\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2 \lt 9-x \\
x + 4 \geqq 3x
\end{array}
\right.
\end{eqnarray}$

　（2）$3x-9 \lt x-3 \lt 6x+7$
　（3）$0.2x-0.1 \leqq 0.1x+0.7 \lt -0.1x+2.1$


⑫
1.次の等式と不等式を解きなさい
　（1）$|2x-5|=3$
　（2）$|3x-1| \lt 1$
　（3）$|3x-2| \geqq x+2$


⑬
1.以下の集合に関する問に答えなさい
　（1）3以下の自然数からなる集合$A$を書き並べて表しなさい
　（2）正の偶数からなる集合$B$を式を用いた形で表せ
　（3）1けたの4の倍数からなる集合$C$の部分集合をすべて書きなさい

2.$D=${$x|x$は$1$けたの奇数}とするとき、次の□に$ \in $または$ \notin $を入れなさい
　（1）$2□D$
　（2）$7□D$
　（3）$13□D$


⑭
1.全体集合$U=${$1,2,3,4,5,6,7,8,9$}の部分集合$A,B$について、
　$A=${$1,2,4,6,8$}
　$B=${$1,3,6,9$}
　のとき、次の集合を求めなさい
　（1）$A \cap B$
　（2）$A \cup B$
　（3）$\overline{A \cap B}$
　（4）$\overline{\overline{A} \cup B}$


⑮
1.次の命題の真偽を調べなさい
　（1）実数$a$について$a \geqq 2$ならば$a \gt 0$
　（2）自然数$m,n$について、$mn$が偶数ならば$m,n$はともに偶数

2.$n^2$が$3$の倍数ならば、$n$は$3$の倍数であることを証明しなさい

問題文全文(内容文)：
数学$\textrm{I}$　2次方程式の解の分離
$x^2+2ax-2a+3=0$
が正の解をもつような
定数$a$の値の範囲を求めよ。

問題文全文(内容文)：
①$y=x^2$のグラフを図示しなさい

②$y=x^2+2x+3$のグラフを図示しなさい

③$y=2x^2+4x+1$を図示しなさい

④$y=3x^2+2x+1$のグラフを図示しなさい

問題文全文(内容文)：
数学$\textrm{I}$　2次方程式の解の分離
$x^2+2ax-2a+3=0$　の解が全て
$-2 \lt x \lt 1$の範囲に存在するような
定数$a$の値の範囲を求めよ。

問題文全文(内容文)：
$F(x,y)=(x-y+1)^2+$$(y-3)^2+$$2,$$0 \leqq x \leqq 1,$$0 \leqq y \leqq 1$の最小値を求めよ。

問題文全文(内容文)：
数学$\textrm{I}$　2次関数の最大最小
$a+b+c=1$　のとき
$a^2+b^2+c^2$の最小値を求めよ。

問題文全文(内容文)：
数学$\textrm{I}$　絶対不等式(4)
$0 \leqq x \leqq 4$のある$x$について
$x^2-2ax+12a+3 \gt 0$
が成り立つような$a$の値の範囲は?

問題文全文(内容文)：
数学$\textrm{I}$　絶対不等式(3)
$0 \leqq x \leqq 4$ の全ての$x$について
$x^2-2ax+2a+3 \gt 0$
が成り立つような$a$の値の範囲は?

問題文全文(内容文)：
入試問題　鹿児島県の公立高等学校

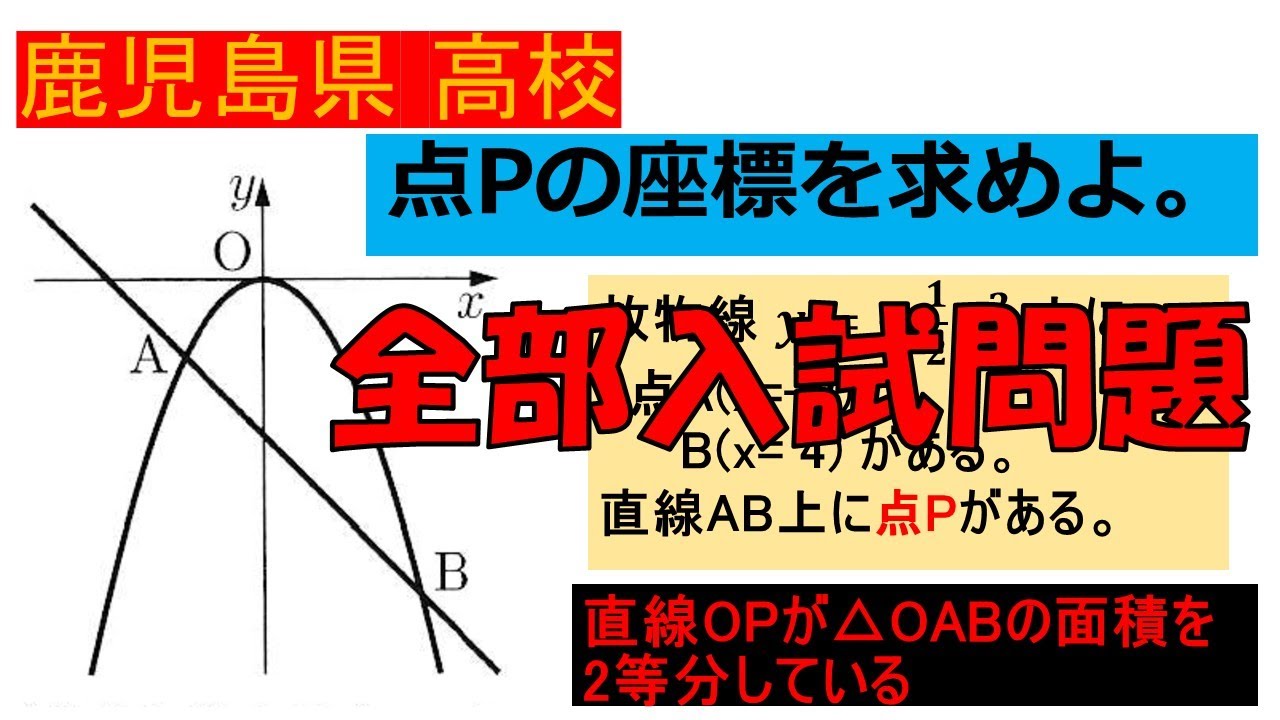
点Pの座標を求めよ。
放物線 $y=\displaystyle \frac{1}{2}x^2$上に
2点$A(x=-2) B(x= 4)$がある。
直線$AB$上に点$P$がある。
直線$OP$が$\triangle OAB$の面積を 2等分している。
※図は動画内参照

問題文全文(内容文)：
$a$を定数とする。
放物線$y=x^2+a$と関数$y=4|x-1|-3$のグラフの共有点の個数を求めよ。

問題文全文(内容文)：
数学$\textrm{I}$　絶対不等式(2)
ある実数$x$に対して
$ax^2 + 4x + a \gt 0$
が成り立つような$a$の値の範囲は?

問題文全文(内容文)：
$f(x)=|2x^2-10x+9|$とおく。
（1）$y=f(x)$のグラフをかけ。
（2）$y=f(x)$のグラフと直線$y=ax+1$がちょうど4個の共通点をもつような、実数の定数$a$の値の範囲を求めよ。

問題文全文(内容文)：
数学$\textrm{I}$　絶対不等式(1)
任意の実数$x$に対して
$ax^2+4x+a \gt 0$
が成り立つような$a$の値の範囲は?

問題文全文(内容文)：
$a$を実数の定義とする。
区間$1 \leqq x \leqq 4$を定義域とする2つの関数$f(x)=ax,g(x)=x^2-4x+9$を考える。
以下の条件を満たすような$a$の範囲をそれぞれ求めよ。
（1）定義域に属するすべての$x$に対して、$f(x) \geqq g(x)$が成り立つ。
（2）定義域に属する$x$で、$f(x) \geqq g(x)$を満たすものがある。
（3）定義域に属するすべての$x_1$と$x_2$に対して、$f(x_1) \geqq g(x_2)$が成り立つ
（4）定義域に属する$x_1$と$x_2$で、$f(x_1) \geqq g(x_2)$を満たすものがある。

問題文全文(内容文)：
$a$を正の実数とする。
2次関数$f(x)=ax^2-2(a+1)x+1$に対して、次の問いに答えよ。
（1）関数$y=f(x)$のグラフの頂点の座標を求めよ。
（2）$0 \leqq x \leqq 2$の範囲で$y=f(x)$の最大値と最小値を求めよ。

問題文全文(内容文)：
数学$\textrm{I}$　2次関数の最大最小(5)
$x^2+4y^2=4$のとき
(1)$x+2y^2$　(2)$xy$
の最大値、最小値を求めよ。

問題文全文(内容文)：
数学$\textrm{I}$　2次関数の最大最小(4)
$x,y$を実数とし、$x \gt 0$とする。
$f(t)=xt^2+yt$　の$0 \leqq t \leqq 1$における
最大値と最小値の差を求めよ。

東大過去問

問題文全文(内容文)：
数学$\textrm{I}$　2次関数の最大最小(3)
$y=(x^2-2ax)^2+4(x^2-2ax)$
の最小値が$-4$となるような定数$a$
の値の範囲を求めよ。

問題文全文(内容文)：
数学$\textrm{I}$　2次関数の最大最小(2)
次の関数の最小値とそのときの$x$を求めよ。
(1)$y=x^4+4x^2-3$
(2)$y=(x^2-2x)^2+4(x^2-2x)-1$

問題文全文(内容文)：
数学$\textrm{I}$　2次関数の最大最小(1)
次の関数の最大最小を調べよ。
(1)　$y=\displaystyle \frac{x^2+6x+6}{x^2+x+1}$　(2)$y=x-\sqrt x$

問題文全文(内容文)：
入試問題　函館ラ・サール高等学校

$a, b$の値を求めなさい。

関数 $y = 2x^2$の
$x$の変域が$-2 \leqq x \leqq a$のとき
$y$の変域が $b \leqq y \leqq 18$である

問題文全文(内容文)：
これを解け.

$x^2-2ix-2-i=0$

問題文全文(内容文)：
【高校数学　数学Ⅰ　二次関数】
$y=x^2+mx+2$が次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)このグラフとx軸の正の部分が異なる2点で交わる。
(2)グラフとx軸のx＜-1の部分が異なる2点で交わる。

問題文全文(内容文)：
【高校数学　数学Ⅰ　二次関数】
$y=x^2+mx+2$が次の条件を満たすように、定数mの値の範囲を定めよ。
(1)このグラフとx軸の正の部分が異なる2点で交わる。

問題文全文(内容文)：
2次関数$f(x)$
$\displaystyle \lim_{h\to 0} \dfrac{f(3+h)-f(3)}{h}=-2$
$\displaystyle \lim_{x\to 1}\dfrac{f(x)-f(1)}{x-1}=2$
$f(47)=0$

(1)$f(x)$と$f(x)$が最大となる$x$
(2)$f(x)\geqq 0$を満たす整数$x$の個数を求めよ.
(3)自然数$k$,$f(x)\geqq k$を満たす$k$が$21$個である$k$の範囲を求めよ.
(4)$f(x)\geqq y$を満たす正の整数の組$(x,y)$の個数を求めよ.

2021近畿大(医)過去問

問題文全文(内容文)：
${\large第1問}$
[1]　$a,b$を定数とするとき、$x$についての不等式
$|ax-b-7| \lt 3$　$\cdots$①
を考える。
(1)$a=-3,b=-2$とする。①を満たす整数全体の集合を$P$とする。
この集合$P$を、要素を書き並べて表すと
$P=\left\{\boxed{\ \ アイ\ \ },　\boxed{\ \ ウエ\ \ }\right\}$
となる。ただし、$\boxed{\ \ アイ\ \ },　\boxed{\ \ ウエ\ \ }$の解答の順序は問わない。

(2)$a=\displaystyle \frac{1}{\sqrt2}$とする。
$(\textrm{i})b=1$のとき、①を満たす整数は全部で$\boxed{\ \ オ\ \ }$個である。
$(\textrm{ii})$①を満たす整数が全部で$(\boxed{\ \ オ\ \ }+1)$個であるような正の整数$b$
のうち、最小のものは$\boxed{\ \ カ\ \ }$である。

[2]平面上に2点$A,B$があり、$AB=8$である。直線$AB$上にない点$P$をとり、
$\triangle ABP$をつくり、その外接円の半径を$R$とする。
太郎さんは、図1(※動画参照)のように、コンピュータソフトを使って点$P$
をいろいろな位置に取った。
図1は、点$P$をいろいろな位置にとったときの$\triangle$の外接円をかいたものである。

(1)太郎さんは、点$P$のとり方によって外接円の半径が異なることに気づき、
次の問題1を考えることにした。

問題1:点$P$をいろいろな位置にとるとき、外接円の半径$R$が最小となる
$\triangle ABP$はどのような三角形か。
正弦定理により、$2R=\displaystyle \frac{\boxed{\ \ キ\ \ }}{\sin\angle APB}$である。よって、
Rが最小となるのは$\angle APB=\boxed{\ \ クケ\ \ }°$の三角形である。
このとき、$R=\boxed{\ \ コ\ \ }$である。


(2)太郎さんは、図2(※動画参照)のように、問題1の点$P$のとり方に
条件を付けて、次の問題2を考えた。

問題2:直線$AB$に平行な直線を$l$とし、直線l上で点$P$をいろいろな
位置にとる。このとき、外接円の半径$R$が最小となる$\triangle ABP$は
どのような三角形か。

太郎さんは、この問題を解決するために、次の構想を立てた。

問題2の解決の構想
問題1の考察から、線分$AB$を直径とする円を$C$とし、円$C$に着目
する。直線lは、その位置によって、円$C$と共有点を持つ場合と
もたない場合があるので、それぞれの場合に分けて考える。

直線$AB$と直線lとの距離を$h$とする。直線lが円$C$と共有点を
持つ場合は、$h \leqq \boxed{\ \ サ\ \ }$のときであり、共有点をもたない場合は、
$h \gt \boxed{\ \ サ\ \ }$のときである。

$(\textrm{i})h \leqq \boxed{\ \ サ\ \ }$のとき
直線$l$が円$C$と共有点をもつので、$R$が最小となる$\triangle ABP$は、
$h \lt \boxed{\ \ サ\ \ }$のとき$\boxed{\boxed{\ \ シ\ \ }}$であり、$h=\boxed{\ \ サ\ \ }$のとき直角二等辺三角形
である。

$(\textrm{ii})h \gt \boxed{\ \ サ\ \ }$のとき
線分$AB$の垂直二等分線を$m$とし、直線$m$と直線$l$との交点を$P_1$とする。
直線$l$上にあり点$P_1$とは異なる点を$P_2$とするとき$\sin\angle AP_1B$
と$\sin\angle AP_2B$の大小を考える。
$\triangle ABP_2$の外接円と直線$m$との共有点のうち、直線$AB$に関して点$P_2$
と同じ側にある点を$P_3$とすると、$\angle AP_3B \boxed{\boxed{\ \ ス\ \ }}\angle AP_2B$である。
また、$\angle AP_3B \lt \angle AP_1B \lt 90°$より$\sin \angle AP_3B \boxed{\boxed{\ \ セ\ \ }}\angle AP_1B$である。
このとき$(\triangle ABP_1$の外接円の半径$) \boxed{\boxed{\ \ ソ\ \ }} (\triangle ABP_2$の外接円の半径)
であり、$R$が最小となる$\triangle ABP$は$\boxed{\boxed{\ \ タ\ \ }}$である。

$\boxed{\boxed{\ \ シ\ \ }},　\boxed{\boxed{\ \ タ\ \ }}$については、最も適当なものを、次の⓪～④のうち
から一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
⓪鈍角三角形　①直角三角形　②正三角形
③二等辺三角形　④直角二等辺三角形

$\boxed{\boxed{\ \ ス\ \ }}～\boxed{\boxed{\ \ ソ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\lt$　①$=$　②$\gt$

(3)問題2の考察を振り返って、$h=8$のとき、$\triangle ABP$の外接円の半径$R$
が最小である場合について考える。このとき、$\sin\angle APB=\displaystyle \frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$
であり、$R=\boxed{\ \ テ\ \ }$である。

2021共通テスト過去問

問題文全文(内容文)：
放物線y=-2x²-12x-14を平行移動して、放物線y=-2x²+4x-3に重ねるには、どのように平行移動するとよいか。

問題文全文(内容文)：
次の座標やグラフを①x軸に関して、②y軸に関して、③原点に関して、それぞれ対称移動したときの座標や式を求めよう。
(1)$ (4,-3)$
(2)$y=-\dfrac{1}{3x^2}-2x+1$