２次関数
２次関数
【数Ⅰ】【2次関数】2次関数の最大最小場合分け1 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
aは正の定数とする。関数$y=x^2-2x-1 (0\leqq x\leqq a)$について、次の問いに答えよ。
(1) 最小値を求めよ
(2) 最大値を求めよ
この動画を見る
aは正の定数とする。関数$y=x^2-2x-1 (0\leqq x\leqq a)$について、次の問いに答えよ。
(1) 最小値を求めよ
(2) 最大値を求めよ
【数Ⅰ】【2次関数】条件付きの解 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)２次関数$y=x^2+mx+1$において、$y$の値が常に正常である。
(2) 放物線$y=x^2+2mx+3m-2$が$y<0$の部分を通らない。
(3) 関数$y=mx^2+4x+m-3$において、$y$の値が常に負である。
２次関数$y=x^2-mx+m+3$のグラフの頂点が第１象限にあるとき、定数$m$の値の範囲を求めよ。
この動画を見る
次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)２次関数$y=x^2+mx+1$において、$y$の値が常に正常である。
(2) 放物線$y=x^2+2mx+3m-2$が$y<0$の部分を通らない。
(3) 関数$y=mx^2+4x+m-3$において、$y$の値が常に負である。
２次関数$y=x^2-mx+m+3$のグラフの頂点が第１象限にあるとき、定数$m$の値の範囲を求めよ。
【数Ⅰ】【2次関数】2次関数 解の個数、連立 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$m$は定数とする。放物線$y=x^2+(m+3)x+3m+4$と$x$軸の共有点の個数を調べよ。
次の2次不等式の解がすべての実数であるとき、定数$m$の値の範囲を求めよ。
(1)$x^2-mx+1＞0$(2)$x^2+mx+2m\leqq0$
次の連立不等式を満たす整数$x$の値を全て求めよ。
\begin{eqnarray}
(1)\left\{
\begin{array}{l}
2x^2-x-3＜0\\
3x^2-10x+3＜0
\end{array}
\right.
(2)\left\{
\begin{array}{l}
x^2+2x>1\\
x^2-x\leqq6
\end{array}
\right.
\end{eqnarray}
この動画を見る
$m$は定数とする。放物線$y=x^2+(m+3)x+3m+4$と$x$軸の共有点の個数を調べよ。
次の2次不等式の解がすべての実数であるとき、定数$m$の値の範囲を求めよ。
(1)$x^2-mx+1＞0$(2)$x^2+mx+2m\leqq0$
次の連立不等式を満たす整数$x$の値を全て求めよ。
\begin{eqnarray}
(1)\left\{
\begin{array}{l}
2x^2-x-3＜0\\
3x^2-10x+3＜0
\end{array}
\right.
(2)\left\{
\begin{array}{l}
x^2+2x>1\\
x^2-x\leqq6
\end{array}
\right.
\end{eqnarray}
【数Ⅰ】【2次関数】解の範囲 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題1
次の方程式が実数解をもつように、実数 $m$ の値の範囲を定めよ。
$(1)\, x^2+2mx+3=0$
$(2)\, x^2+mx+m=0$
問題2
2次方程式 $x^2-2mx-4m=0$ が次の条件を満たすように、定数 $m$ の値の範囲を定めよ。
$(1)$ 異なる2つの実数解をもつ
$(2)$ 実数解をもたない
問題3
次の条件を満たすように、実数 $m$ の値の範囲を定めよ。
$(1)$ 2次関数 $y=x^2-2mx+2m+3$ のグラフが $x$ 軸と共有点をもつ
$(2)$ 2次関数 $y=x^2+2mx-m+2$ のグラフが $x$ 軸と共有点をもたない
この動画を見る
問題1
次の方程式が実数解をもつように、実数 $m$ の値の範囲を定めよ。
$(1)\, x^2+2mx+3=0$
$(2)\, x^2+mx+m=0$
問題2
2次方程式 $x^2-2mx-4m=0$ が次の条件を満たすように、定数 $m$ の値の範囲を定めよ。
$(1)$ 異なる2つの実数解をもつ
$(2)$ 実数解をもたない
問題3
次の条件を満たすように、実数 $m$ の値の範囲を定めよ。
$(1)$ 2次関数 $y=x^2-2mx+2m+3$ のグラフが $x$ 軸と共有点をもつ
$(2)$ 2次関数 $y=x^2+2mx-m+2$ のグラフが $x$ 軸と共有点をもたない
【数Ⅰ】【2次関数】点の通過 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題1
次の条件を満たす放物線の方程式を求めよ。
$(1)$ 3点 $(-4,0), \, (-2,0), \, (0,-4)$ を通る。
$(2)$ 点 $(2,0)$ で $x$ 軸に接し、点 $(-2,12)$ を通る。
問題2
$a, \, b, \, c$ の値を入力すると、関数 $y=ax^2+bx+c$ のグラフが表示されるコンピュータソフトがある。ある $a, \, b, \, c$ の値を入力すると、グラフは図のように表示された (図は動画参照)。
$(1)$ $a, \, b, \, c, \, b^2-4ac, \, a+b+c$ の符号をいえ。
$(2)$ この $a, \, b$ の値を変えずに、$c$ の値だけを変化させたとき、変わらないものを次の中からすべて選べ。また、変わらない理由を説明せよ。
① グラフと $x$ 軸の共有点の個数
② グラフの頂点の $x$ 座標の符号
③ グラフの頂点の $y$ 座標の符号
この動画を見る
問題1
次の条件を満たす放物線の方程式を求めよ。
$(1)$ 3点 $(-4,0), \, (-2,0), \, (0,-4)$ を通る。
$(2)$ 点 $(2,0)$ で $x$ 軸に接し、点 $(-2,12)$ を通る。
問題2
$a, \, b, \, c$ の値を入力すると、関数 $y=ax^2+bx+c$ のグラフが表示されるコンピュータソフトがある。ある $a, \, b, \, c$ の値を入力すると、グラフは図のように表示された (図は動画参照)。
$(1)$ $a, \, b, \, c, \, b^2-4ac, \, a+b+c$ の符号をいえ。
$(2)$ この $a, \, b$ の値を変えずに、$c$ の値だけを変化させたとき、変わらないものを次の中からすべて選べ。また、変わらない理由を説明せよ。
① グラフと $x$ 軸の共有点の個数
② グラフの頂点の $x$ 座標の符号
③ グラフの頂点の $y$ 座標の符号
【数Ⅰ】【2次関数】関数の場合分け ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
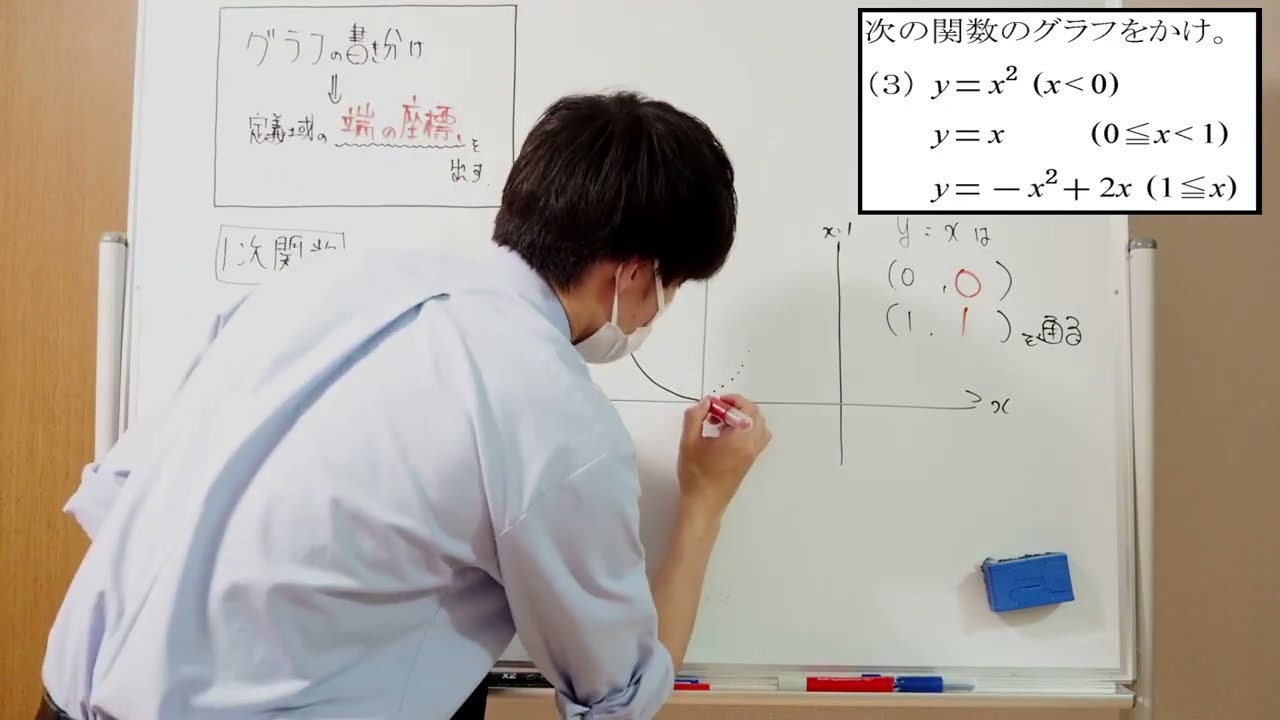
次の関数のグラフをかけ。
(1) y=-x+2 (x<2) , y=x-2 (x≧2)
(2) y=1 (x<0) , y=x+1 (x≧0)
(3) y=x² (x<0) , y=x (0≦x<1) , y=-x²+2x (1≦x)
この動画を見る
次の関数のグラフをかけ。
(1) y=-x+2 (x<2) , y=x-2 (x≧2)
(2) y=1 (x<0) , y=x+1 (x≧0)
(3) y=x² (x<0) , y=x (0≦x<1) , y=-x²+2x (1≦x)
福田の数学〜早稲田大学2024商学部第1問(4)〜放物線と2本の接線で囲まれた図形の面積
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面において、放物線$y=x^2$を$C$とする。点$P(s,t)$から放物線$C$に異なる2本の接線が引け、その接点をそれぞれ$A,B$とする。線分$PA,PB$と放物線$C$で囲まれた図形の面積が$\displaystyle\frac{144}{125}$であるとき$s,t$の満たす方程式は？
この動画を見る
座標平面において、放物線$y=x^2$を$C$とする。点$P(s,t)$から放物線$C$に異なる2本の接線が引け、その接点をそれぞれ$A,B$とする。線分$PA,PB$と放物線$C$で囲まれた図形の面積が$\displaystyle\frac{144}{125}$であるとき$s,t$の満たす方程式は？
福田の数学〜早稲田大学2024教育学部第1問(4)〜領域と奇跡
単元：
#数Ⅰ#数Ⅱ#２次関数#図形と方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
この動画を見る
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
この出し方知ってる？
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
二次関数$y=\frac{1}{2}x^2$上の2点A(-4, 8), B(2, 2)と原点Oを結んでできる三角形の面積を求めよ
この動画を見る
二次関数$y=\frac{1}{2}x^2$上の2点A(-4, 8), B(2, 2)と原点Oを結んでできる三角形の面積を求めよ
#関西大学2024 #方程式_70
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
この動画を見る
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
#関西学院大学2011#方程式_69
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$(x+1)(x-2)(x+3)(x-4)=-24$を解け.
2011関西学院大学過去問題
この動画を見る
$(x+1)(x-2)(x+3)(x-4)=-24$を解け.
2011関西学院大学過去問題
#北海道大学1957#方程式_65
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#一次不等式（不等式・絶対値のある方程式・不等式）#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{10x-10^{-x}}{10x+10^{-x}}=a \ (\vert a \vert \gt 1)$
$x$について解け.
1957北海道大学過去問題
この動画を見る
$\dfrac{10x-10^{-x}}{10x+10^{-x}}=a \ (\vert a \vert \gt 1)$
$x$について解け.
1957北海道大学過去問題
福田のおもしろ数学265〜直交する2つの円柱の共通部分の体積
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
x軸、y軸を軸とする半径1の円柱T_1 , \ T_2の共通部分の体積を求めよ。$（図は動画参照）
この動画を見る
$
x軸、y軸を軸とする半径1の円柱T_1 , \ T_2の共通部分の体積を求めよ。$（図は動画参照）
ルートが入っている二次方程式 広尾学園
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
広尾学園
方程式を解け
$x^{2}-\sqrt{ 2 }(1+\sqrt{ 5 })x+2\sqrt{ 5 }=0$
この動画を見る
広尾学園
方程式を解け
$x^{2}-\sqrt{ 2 }(1+\sqrt{ 5 })x+2\sqrt{ 5 }=0$
二次方程式の応用 三田学園
単元：
#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の2つの二次方程式の共通な解が$x=-2$だけになるときa,bの値を求めよ
$x^{2}-(b+2)x-b^{2}=0$
$x^{2}+ax+2b=0$
この動画を見る
次の2つの二次方程式の共通な解が$x=-2$だけになるときa,bの値を求めよ
$x^{2}-(b+2)x-b^{2}=0$
$x^{2}+ax+2b=0$
福田の数学〜明治大学2024理工学部第3問〜放物線と折れ線の位置関係
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次関数とグラフ#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
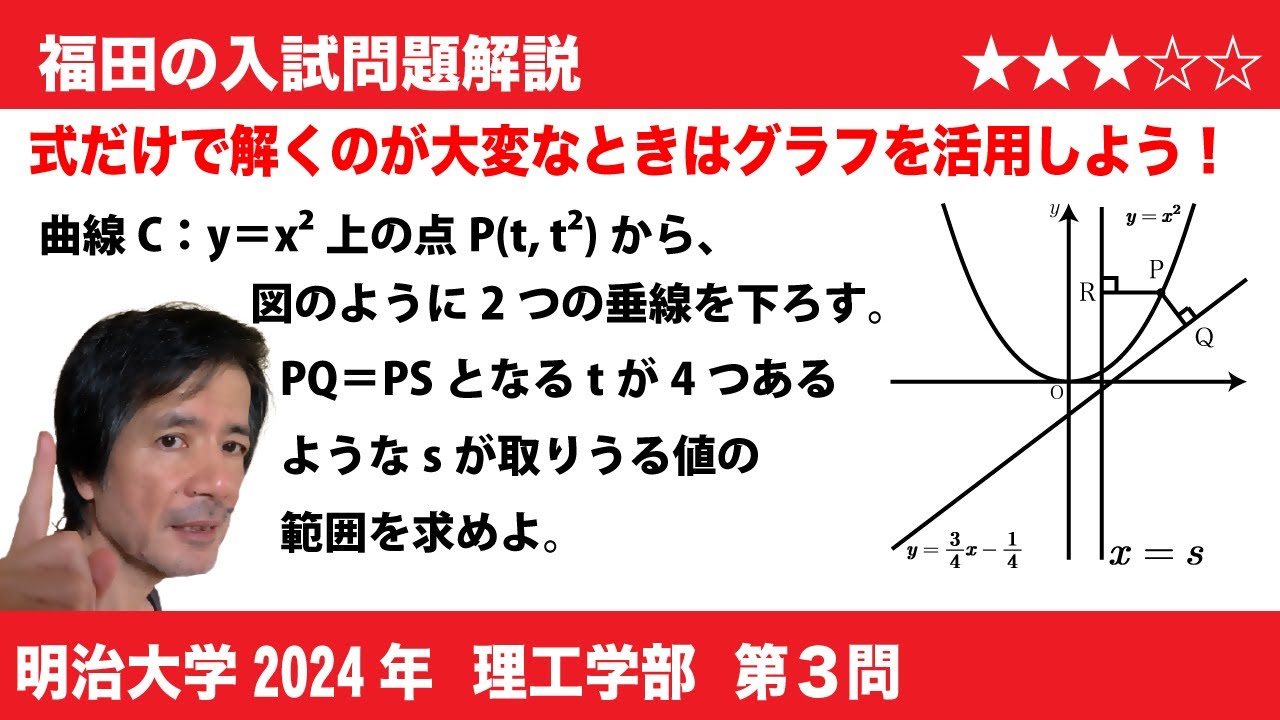
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
この動画を見る
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
よく間違える二次関数の変域
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$-1\leqq x^2\leqq 2のとき、x^2の範囲をもとめよ$
この動画を見る
$-1\leqq x^2\leqq 2のとき、x^2の範囲をもとめよ$
福田の数学〜中央大学2024理工学部第1問〜3つの関数の大小関係と絶対不等式
単元：
#数Ⅰ#２次関数#2次関数とグラフ#微分とその応用#積分とその応用#接線と法線・平均値の定理#関数の変化（グラフ・最大最小・方程式・不等式）#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
この動画を見る
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
2次方程式の応用 （高校数学）
単元：
#２次関数#2次方程式と2次不等式#2次関数とグラフ
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式 $(x-l) (x-2) -(x-k) =0$ の解を $α,β(α<β)$ とするとき、$α,β,l,2, k$ を小さい順に並べよ
この動画を見る
2次方程式 $(x-l) (x-2) -(x-k) =0$ の解を $α,β(α<β)$ とするとき、$α,β,l,2, k$ を小さい順に並べよ
2次方程式の応用 （高校数学）
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式$(x-1)(x-2)-(x-k)=0の解を\mathit{α ,β}(\mathit{α}<\mathit{β})とするとき
\mathit{α,β},1,2,kを小さい順に並べよ。(ただし、1<\mathit{k}<2$)
この動画を見る
2次方程式$(x-1)(x-2)-(x-k)=0の解を\mathit{α ,β}(\mathit{α}<\mathit{β})とするとき
\mathit{α,β},1,2,kを小さい順に並べよ。(ただし、1<\mathit{k}<2$)
【数学】中高一貫校用問題集数式・関数編：2次関数の決定
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の問いに答えよ。
(1)$x^2$の係数が2で、そのグラフが点(1,3)を通り、頂点が直線$y=2x-3$上にあるような2次関数を求めよ。
(2)2次関数$y=x^2-2ax+b$のグラフが点(1,3)を通り、頂点が直線$y=x-10$上にあるとき、定数a,bの値を求めよ。
(3)2次関数$y=2x^2+ax+b$のグラフが点(3,5)を通り、頂点が直線$y=2x-5$上にあるとき、定数a,bの値を求めよ。
この動画を見る
次の問いに答えよ。
(1)$x^2$の係数が2で、そのグラフが点(1,3)を通り、頂点が直線$y=2x-3$上にあるような2次関数を求めよ。
(2)2次関数$y=x^2-2ax+b$のグラフが点(1,3)を通り、頂点が直線$y=x-10$上にあるとき、定数a,bの値を求めよ。
(3)2次関数$y=2x^2+ax+b$のグラフが点(3,5)を通り、頂点が直線$y=2x-5$上にあるとき、定数a,bの値を求めよ。
福田の数学〜中央大学2024経済学部第1問(1)〜絶対値の付いた2次不等式の解
連立方程式 2通りで解説！！ コメント欄に訂正あり。
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の連立方程式を解け
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy=2 \\
yz=6 \\
zx=3
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の連立方程式を解け
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy=2 \\
yz=6 \\
zx=3
\end{array}
\right.
\end{eqnarray}$
最大値＝❓ 分数関数 （高校数学）
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の$y$の最大値を求めよ
$\displaystyle y=\frac{1}{x^2-4x+6}$
この動画を見る
次の$y$の最大値を求めよ
$\displaystyle y=\frac{1}{x^2-4x+6}$
福田の数学〜千葉大学2024年文系第3問〜絶対値の付いた放物線と直線の位置関係
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a$を実数とする。$f(x)=x^2-ax+a^2-2$について、以下の問いに答えよ。
(1) $y=f(x)$のグラフと$x$軸が$x > 0$の範囲に共有点を2個もつような、$a$の値の範囲を求めよ。
(2) $k$を正の定数とし、$g(x)=kx$とする。$a$が(1)の範囲にあるとき、$y=|f(x)|$のグラフと$y=g(x)$のグラフの共有点がちょうど3個となるような$k$を求めよ。
この動画を見る
$a$を実数とする。$f(x)=x^2-ax+a^2-2$について、以下の問いに答えよ。
(1) $y=f(x)$のグラフと$x$軸が$x > 0$の範囲に共有点を2個もつような、$a$の値の範囲を求めよ。
(2) $k$を正の定数とし、$g(x)=kx$とする。$a$が(1)の範囲にあるとき、$y=|f(x)|$のグラフと$y=g(x)$のグラフの共有点がちょうど3個となるような$k$を求めよ。
福田のおもしろ数学189〜xyzの関係式からzの最大最小を決定する
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x, \, y, \, z$ は実数で
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z = 1 \\
x^2 + y^2 + z^2 = 3
\end{array}
\right.
\end{eqnarray}$
のとき、$z$ の最大値と最小値、そのときの $x, \, y$ を求めよ。
この動画を見る
$x, \, y, \, z$ は実数で
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z = 1 \\
x^2 + y^2 + z^2 = 3
\end{array}
\right.
\end{eqnarray}$
のとき、$z$ の最大値と最小値、そのときの $x, \, y$ を求めよ。
【数学受験組の実力チェック】三平方の定理と二次方程式の解の公式を証明せよ【東大・早稲田・国立志望】
単元：
#数学(中学生)#中３数学#２次方程式#数Ⅰ#２次関数#三平方の定理#2次方程式と2次不等式#数学(高校生)
指導講師：
Morite2 English Channel
問題文全文(内容文)：
数学系YouTuberの鈴木貫太郎先生が「三平方の定理」と「二次方程式の解の公式」を証明します。
考え方を学んで、復習の参考にしましょう！
この動画を見る
数学系YouTuberの鈴木貫太郎先生が「三平方の定理」と「二次方程式の解の公式」を証明します。
考え方を学んで、復習の参考にしましょう！
福田の数学〜名古屋大学2024年文系第2問〜放物線と直線の関係
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ $t$を0でない実数として、$x$の関数$y$=$-x^2$+$tx$+$t$ のグラフを$C$とする。
(1)$C$上において$y$座標が最大となる点Pの座標を求めよ。
(2)Pと点O(0,0)を通る直線を$l$とする。$l$と$C$がP以外の共有点Qを持つために$t$が満たすべき条件を求めよ。また、そのとき、点Qの座標を求めよ。
(3)$t$は(2)の条件を満たすとする。A(-1,-2)として、$X$=$\displaystyle\frac{1}{4}t^2$+$t$ とおくとき、AP$^2$－AQ$^2$を$X$で表せ。また、AP<AQとなるために$t$が満たすべき条件を求めよ。
この動画を見る
$\Large\boxed{2}$ $t$を0でない実数として、$x$の関数$y$=$-x^2$+$tx$+$t$ のグラフを$C$とする。
(1)$C$上において$y$座標が最大となる点Pの座標を求めよ。
(2)Pと点O(0,0)を通る直線を$l$とする。$l$と$C$がP以外の共有点Qを持つために$t$が満たすべき条件を求めよ。また、そのとき、点Qの座標を求めよ。
(3)$t$は(2)の条件を満たすとする。A(-1,-2)として、$X$=$\displaystyle\frac{1}{4}t^2$+$t$ とおくとき、AP$^2$－AQ$^2$を$X$で表せ。また、AP<AQとなるために$t$が満たすべき条件を求めよ。
２次不等式はこの手順通りに考えれば解けちゃう!? #数学 #高校数学 #不等式
【高校数学】２次不等式はこれでマスター！この手順通りに考えれば解けちゃう【数学のコツ】
