 三角比への応用(正弦・余弦・面積)
三角比への応用(正弦・余弦・面積)
 三角比への応用(正弦・余弦・面積)
三角比への応用(正弦・余弦・面積)
京大の三角比!気づければ簡単!【数学 入試問題】【京都大学】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\alpha,\beta$が$a>0°,\beta>0°,\alpha+\beta<180°$かつ$sin^2\alpha+sin^2\beta=sin^2(\alpha+\beta)$を満たすとき、
$sin\alpha+sin\beta$の取りうる範囲を求めよ。
京都大過去問
この動画を見る
$\alpha,\beta$が$a>0°,\beta>0°,\alpha+\beta<180°$かつ$sin^2\alpha+sin^2\beta=sin^2(\alpha+\beta)$を満たすとき、
$sin\alpha+sin\beta$の取りうる範囲を求めよ。
京都大過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第5問〜三角比と空間図形の計量

単元:
#数Ⅰ#大学入試過去問(数学)#空間図形#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
半径$4\sqrt2$の球面S上に3点A,B,Cがあり、線分AB,BC,CAの長さはそれぞれ$AB=4\sqrt6,BC=10,C=6$とする。
(1)$\cos\angle ABC=\boxed{\ \ テ\ \ }$である。平面ABCで球面Sを切った切り口の円をTとする。
Tの半径は$\boxed{\ \ ト\ \ }$である。点Dが円T上を動くとき、$\triangle DAB$の面積の最大値は
$\boxed{\ \ ナ\ \ }$である。
(2)球面Sの中心Oから平面ABCに下ろした垂線OHの長さは$\boxed{\ \ ニ\ \ }$である。
(3)点Eは球面S上を動くとき、三角錐EABCの体積の最大値は$\boxed{\ \ ヌ\ \ }$である。
2022慶應義塾大学理工学部過去問
この動画を見る
半径$4\sqrt2$の球面S上に3点A,B,Cがあり、線分AB,BC,CAの長さはそれぞれ$AB=4\sqrt6,BC=10,C=6$とする。
(1)$\cos\angle ABC=\boxed{\ \ テ\ \ }$である。平面ABCで球面Sを切った切り口の円をTとする。
Tの半径は$\boxed{\ \ ト\ \ }$である。点Dが円T上を動くとき、$\triangle DAB$の面積の最大値は
$\boxed{\ \ ナ\ \ }$である。
(2)球面Sの中心Oから平面ABCに下ろした垂線OHの長さは$\boxed{\ \ ニ\ \ }$である。
(3)点Eは球面S上を動くとき、三角錐EABCの体積の最大値は$\boxed{\ \ ヌ\ \ }$である。
2022慶應義塾大学理工学部過去問
簡単すぎる京大の入試問題!解けますか?【数学】【京都大学】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\triangle ABC$において、$AB=2,AC=1$とする。$\angle BAC$の二等分線と辺$BC$の交点を$D$とする。$AD=BD$となるとき、$\triangle ABC$の面積を求めよ。
京都大過去問
この動画を見る
$\triangle ABC$において、$AB=2,AC=1$とする。$\angle BAC$の二等分線と辺$BC$の交点を$D$とする。$AD=BD$となるとき、$\triangle ABC$の面積を求めよ。
京都大過去問
福田の数学〜千葉大学2022年理系第2問〜三角形と三角比

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、原点Oと点A(1,0)と点B(0,1)がある。$0 \lt t \lt 1$に対し、
線分BO,OA,ABのそれぞれを$t:(1-t)$に内分する点をP,Q,Rとする。
(1)$\triangle PQR$の面積をtの式で表せ。
(2)$\triangle PQR$が二等辺三角形になるときのtの値を全て求めよ。
(3)$\theta = \angle RPQ$とする。(2)それぞれの場合に$\cos\theta$を求めよ。
2022千葉大学理系過去問
この動画を見る
座標平面において、原点Oと点A(1,0)と点B(0,1)がある。$0 \lt t \lt 1$に対し、
線分BO,OA,ABのそれぞれを$t:(1-t)$に内分する点をP,Q,Rとする。
(1)$\triangle PQR$の面積をtの式で表せ。
(2)$\triangle PQR$が二等辺三角形になるときのtの値を全て求めよ。
(3)$\theta = \angle RPQ$とする。(2)それぞれの場合に$\cos\theta$を求めよ。
2022千葉大学理系過去問
福田の数学〜一橋大学2022年文系第2問〜平面上の三角形の面積の最大値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}\ 0 \leqq \theta \lt 2\pi$とする。
座標平面上の3点O(0,0), $P(\cos\theta,\sin\theta)$, $Q(1,3\sin2\theta)$
が三角形をなすとき、$\triangle OPQ$の面積の最大値を求めよ。
2022一橋大学文系過去問
この動画を見る
${\Large\boxed{2}}\ 0 \leqq \theta \lt 2\pi$とする。
座標平面上の3点O(0,0), $P(\cos\theta,\sin\theta)$, $Q(1,3\sin2\theta)$
が三角形をなすとき、$\triangle OPQ$の面積の最大値を求めよ。
2022一橋大学文系過去問
正五角形の作図と証明

tan

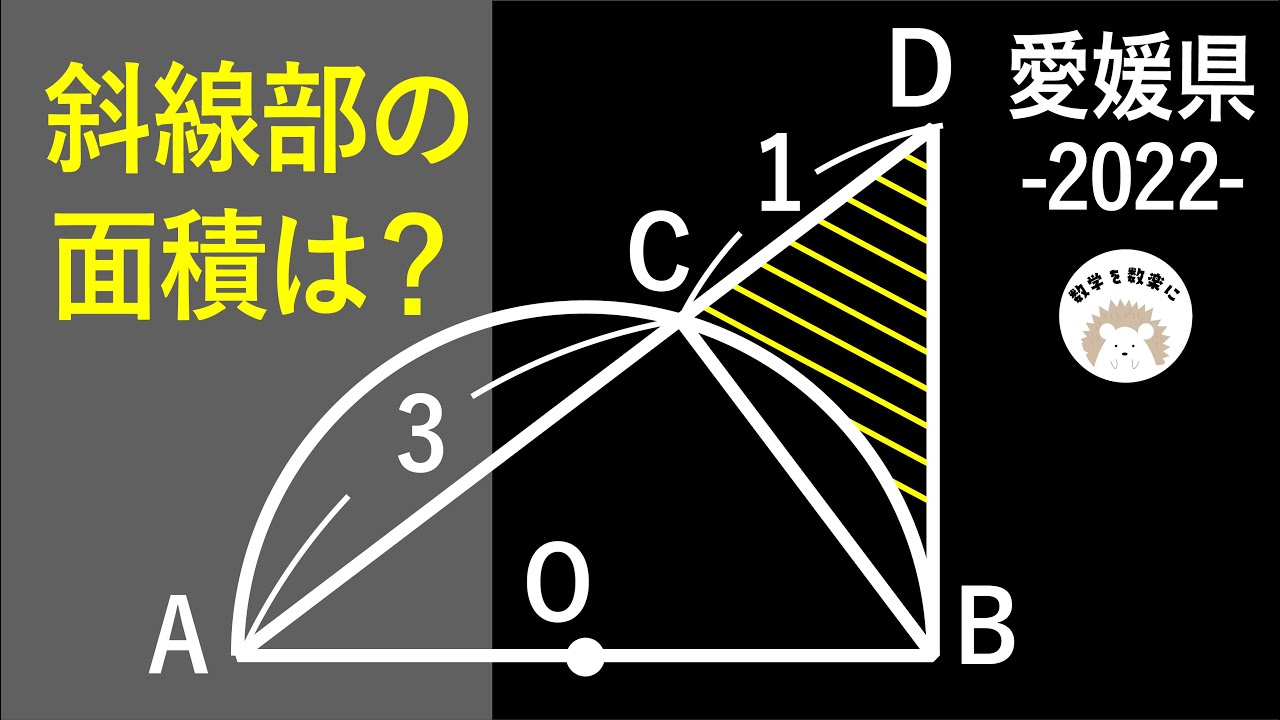
おうぎ形と正方形 令和4年度 愛媛県ラスト問題(改) 数学 2022 入試問題100題解説83問目!
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積は?
*図は動画内参照
2022愛媛県
この動画を見る
斜線部の面積は?
*図は動画内参照
2022愛媛県
三角比の拡張 #Shorts
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
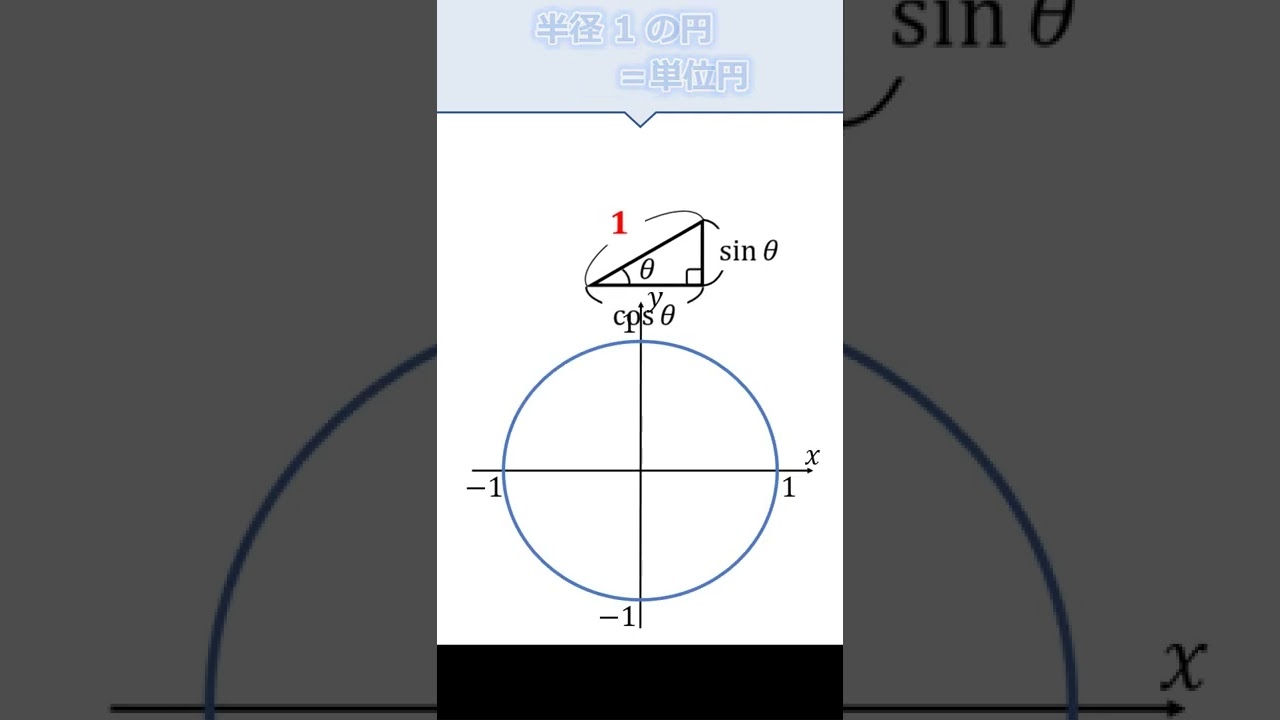
三角比の拡張に関して解説していきます.
この動画を見る
三角比の拡張に関して解説していきます.
2022年東京大 (理系)最初の一問!!

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$f(x)=(cosx)log(cosx) -cosx + \int_0^x(cost)log(cost)dt$
f(x)は区間$0<x< \frac{π}{2}$において最小値を持つことを示し、その最小値を求めよ。
2022東京大学理系問題文改め
この動画を見る
$f(x)=(cosx)log(cosx) -cosx + \int_0^x(cost)log(cost)dt$
f(x)は区間$0<x< \frac{π}{2}$において最小値を持つことを示し、その最小値を求めよ。
2022東京大学理系問題文改め
【数学Ⅰ/三角比】円に内接する四角形②
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
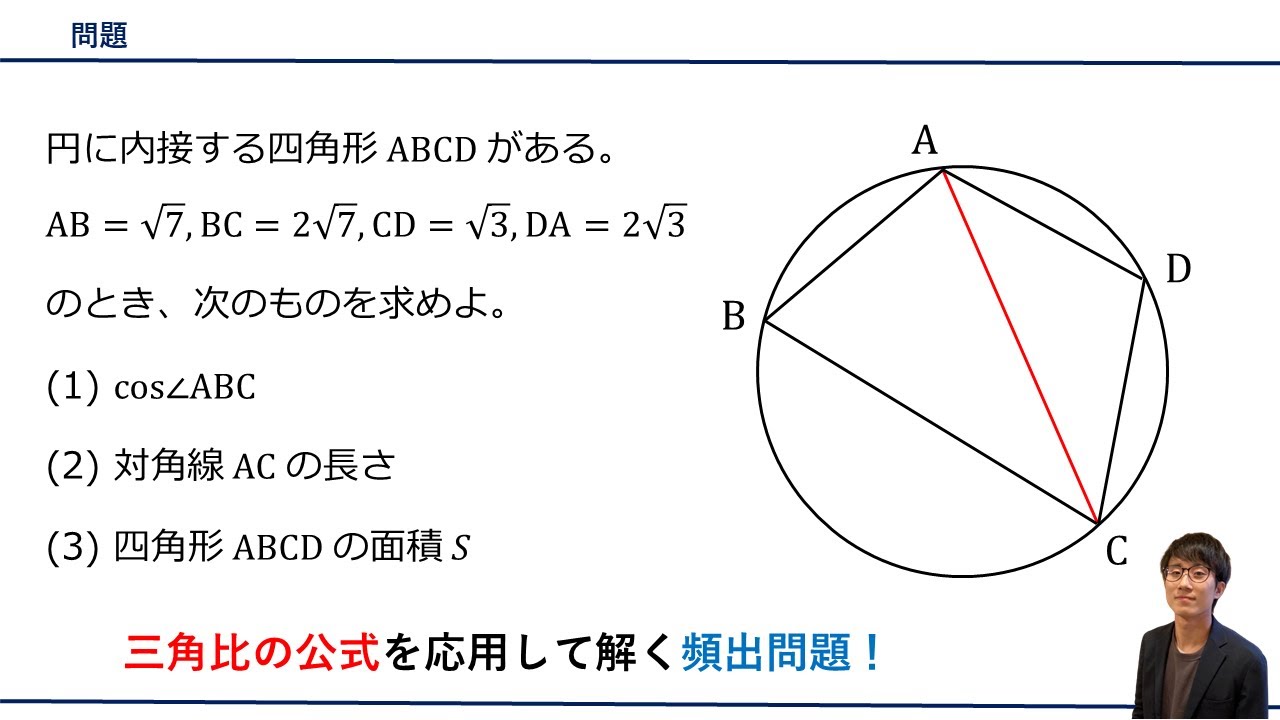
円に内接する四角形$ABCD$がある。
$AB=\sqrt{ 7 },BC=2\sqrt{ 7 },CD=\sqrt{ 3 },DA=2\sqrt{ 3 }$のとき、次のものを求めよ。
(1)
$\cos\angle ABC$
(2)
対角線$AC$の長さ
(3)
四角形$ABCD$の面積$S$
この動画を見る
円に内接する四角形$ABCD$がある。
$AB=\sqrt{ 7 },BC=2\sqrt{ 7 },CD=\sqrt{ 3 },DA=2\sqrt{ 3 }$のとき、次のものを求めよ。
(1)
$\cos\angle ABC$
(2)
対角線$AC$の長さ
(3)
四角形$ABCD$の面積$S$
【数学Ⅰ/三角比】円に内接する四角形①
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
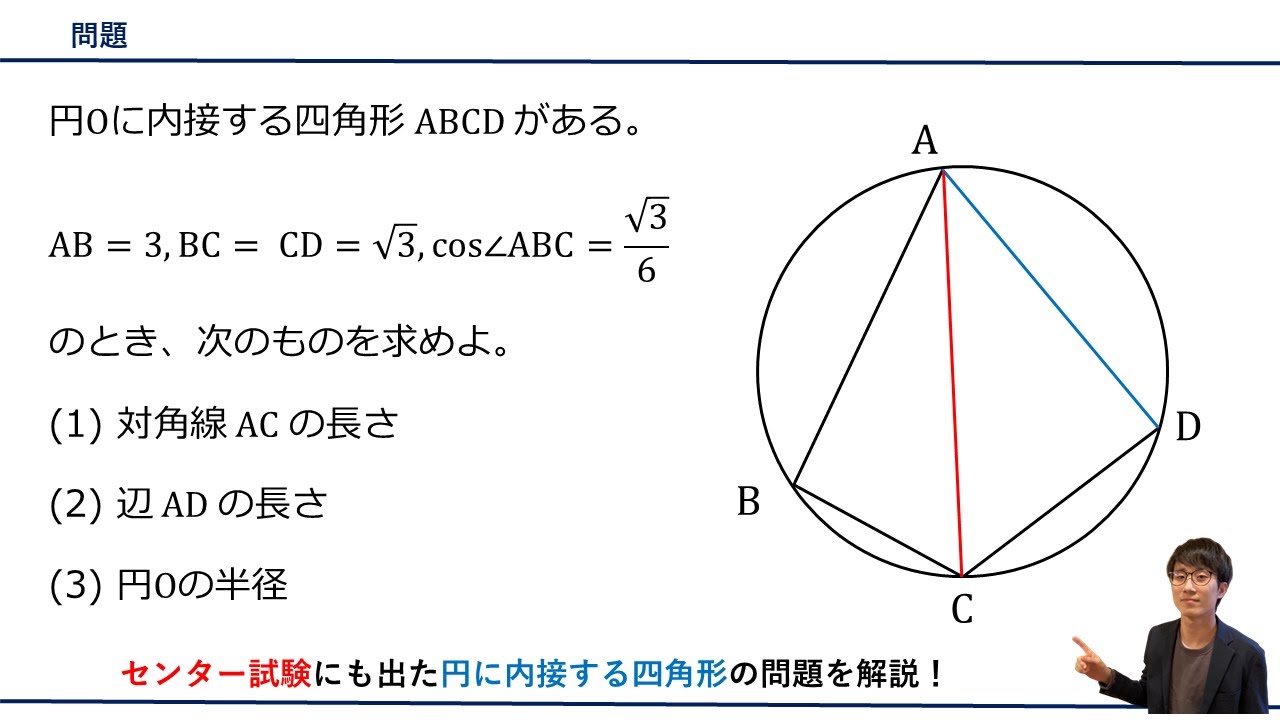
円$O$に内接する四角形$ABCD$がある。
$AB=3,$ $BC=CD=\sqrt{ 3 },$ $\cos\angle ABC=\displaystyle \frac{\sqrt{ 3 }}{6}$のとき、次のものを求めよ。
(1)対角線$AC$の長さ
(2)辺$AD$の長さ
(3)円$O$の半径
この動画を見る
円$O$に内接する四角形$ABCD$がある。
$AB=3,$ $BC=CD=\sqrt{ 3 },$ $\cos\angle ABC=\displaystyle \frac{\sqrt{ 3 }}{6}$のとき、次のものを求めよ。
(1)対角線$AC$の長さ
(2)辺$AD$の長さ
(3)円$O$の半径
【数学Ⅰ/三角比】正弦定理を使って辺の比を求める問題

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$\triangle ABC$において、$\displaystyle \frac{\sin A}{4}=\displaystyle \frac{\sin B}{5}=\displaystyle \frac{\sin C}{2}$が成立しているとき、次の問いに答えよ。
(1)3辺の比$a:b:c$を求めよ。
(2)$\cos B$の値を求めよ。
この動画を見る
$\triangle ABC$において、$\displaystyle \frac{\sin A}{4}=\displaystyle \frac{\sin B}{5}=\displaystyle \frac{\sin C}{2}$が成立しているとき、次の問いに答えよ。
(1)3辺の比$a:b:c$を求めよ。
(2)$\cos B$の値を求めよ。
【数学Ⅰ/三角比】余弦定理の使い方

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$\triangle ABC$において、次の値を求めよ。
(1)$a=2\sqrt{ 3 },b=3,c=30^{ \circ }$のとき、$C$。
(2)$a=8,b=5,c=7$のとき、$C$。
この動画を見る
$\triangle ABC$において、次の値を求めよ。
(1)$a=2\sqrt{ 3 },b=3,c=30^{ \circ }$のとき、$C$。
(2)$a=8,b=5,c=7$のとき、$C$。
【数学Ⅰ/三角比】正弦定理の使い方

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$\triangle ABC$において、$a=2\sqrt{ 2 },b=2,A=45^{ \circ }$のとき、$B$および外接円の半径$R$を求めよ。
この動画を見る
$\triangle ABC$において、$a=2\sqrt{ 2 },b=2,A=45^{ \circ }$のとき、$B$および外接円の半径$R$を求めよ。
cosで合成 2通りで解説!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2}cosθ+\frac{\sqrt 3}{2} sinθ$を
$▢cos(θ - ○)$の形に直せ
この動画を見る
$\frac{1}{2}cosθ+\frac{\sqrt 3}{2} sinθ$を
$▢cos(θ - ○)$の形に直せ
sin sin sin sin sin sin sin sin sin sin sin sin
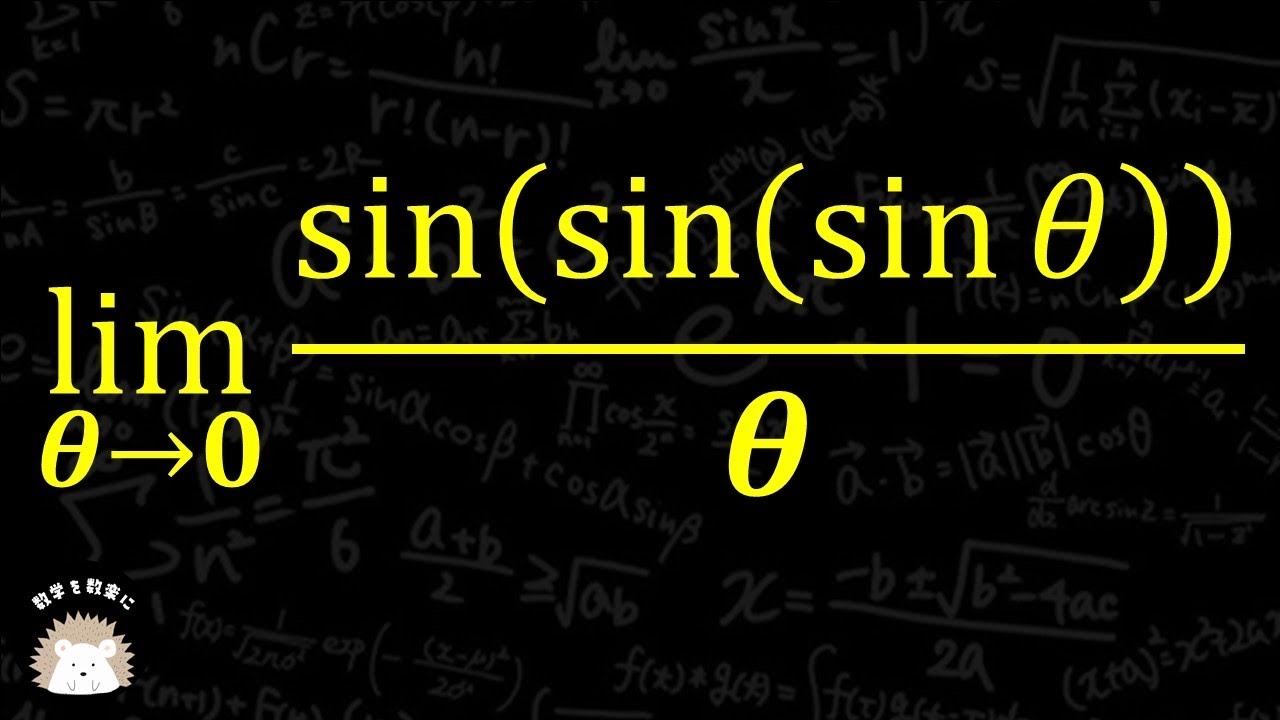
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\displaystyle \lim_{ θ \to 0 } \frac{sin(sin(sin θ))}{θ}
$
この動画を見る
$
\displaystyle \lim_{ θ \to 0 } \frac{sin(sin(sin θ))}{θ}
$
図形的イメージ
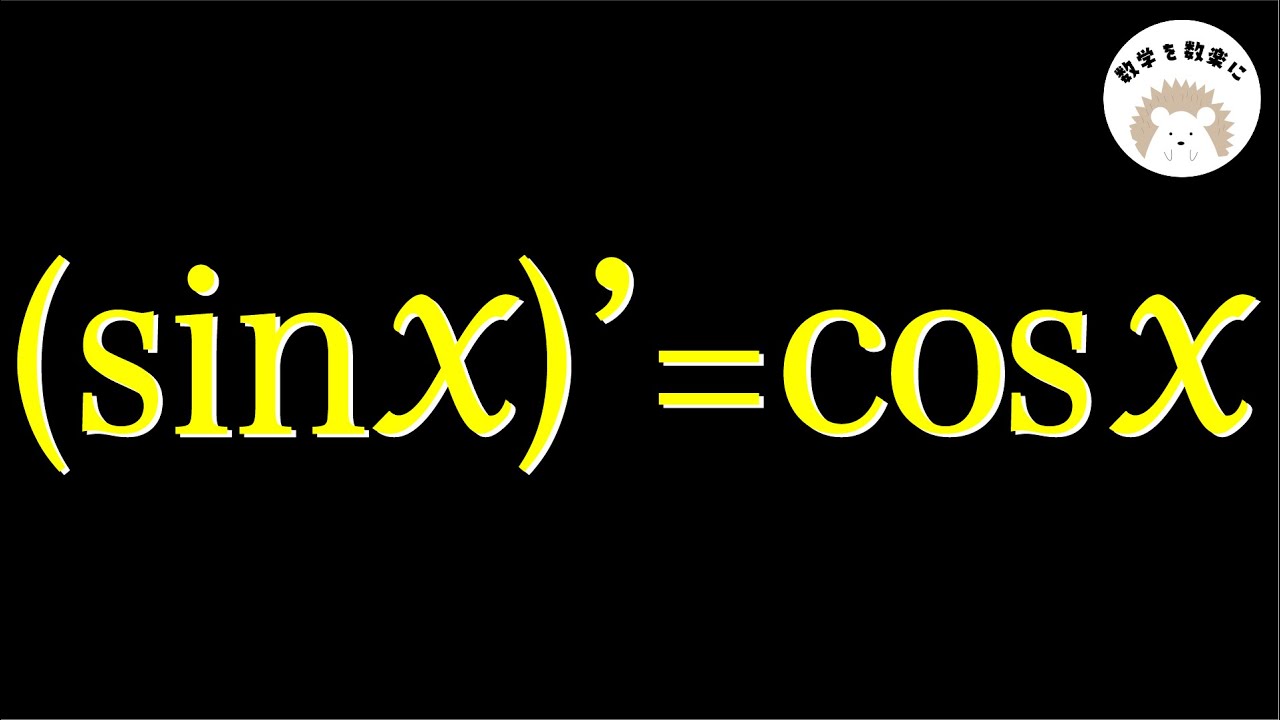
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(sinx)' = cosx
この動画を見る
(sinx)' = cosx
福田の共通テスト解答速報〜2022年共通テスト数学IA問題1[3]。三角比と図形の問題。

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第1問\ [3] 外接円の半径が3である$\triangle ABC$を考える。点Aから直線BCへ引いた垂線と直線BC
との交点をDとする。
(1)$AB=5, AC=4$とする。このとき$\sin\angle ABC=\frac{\boxed{ソ}}{\boxed{タ}}, AD=\frac{\boxed{チツ}}{\boxed{テ}}$ である。
(2) 2辺AB,ACの長さの間に$2AB+AC=14$の関係があるとする。
このとき、ABの長さの取り得る値の範囲は$\boxed{ト} \leqq AB \leqq \boxed{ナ}$であり、
$AD=\frac{\boxed{ニヌ}}{\boxed{ネ}}AB^2+\frac{\boxed{ノ}}{\boxed{ハ}}AB$と表せるので、ADの長さの最大値は$\boxed{ヒ}$である。
2022共通テスト数学過去問
この動画を見る
第1問\ [3] 外接円の半径が3である$\triangle ABC$を考える。点Aから直線BCへ引いた垂線と直線BC
との交点をDとする。
(1)$AB=5, AC=4$とする。このとき$\sin\angle ABC=\frac{\boxed{ソ}}{\boxed{タ}}, AD=\frac{\boxed{チツ}}{\boxed{テ}}$ である。
(2) 2辺AB,ACの長さの間に$2AB+AC=14$の関係があるとする。
このとき、ABの長さの取り得る値の範囲は$\boxed{ト} \leqq AB \leqq \boxed{ナ}$であり、
$AD=\frac{\boxed{ニヌ}}{\boxed{ネ}}AB^2+\frac{\boxed{ノ}}{\boxed{ハ}}AB$と表せるので、ADの長さの最大値は$\boxed{ヒ}$である。
2022共通テスト数学過去問
超有名問題
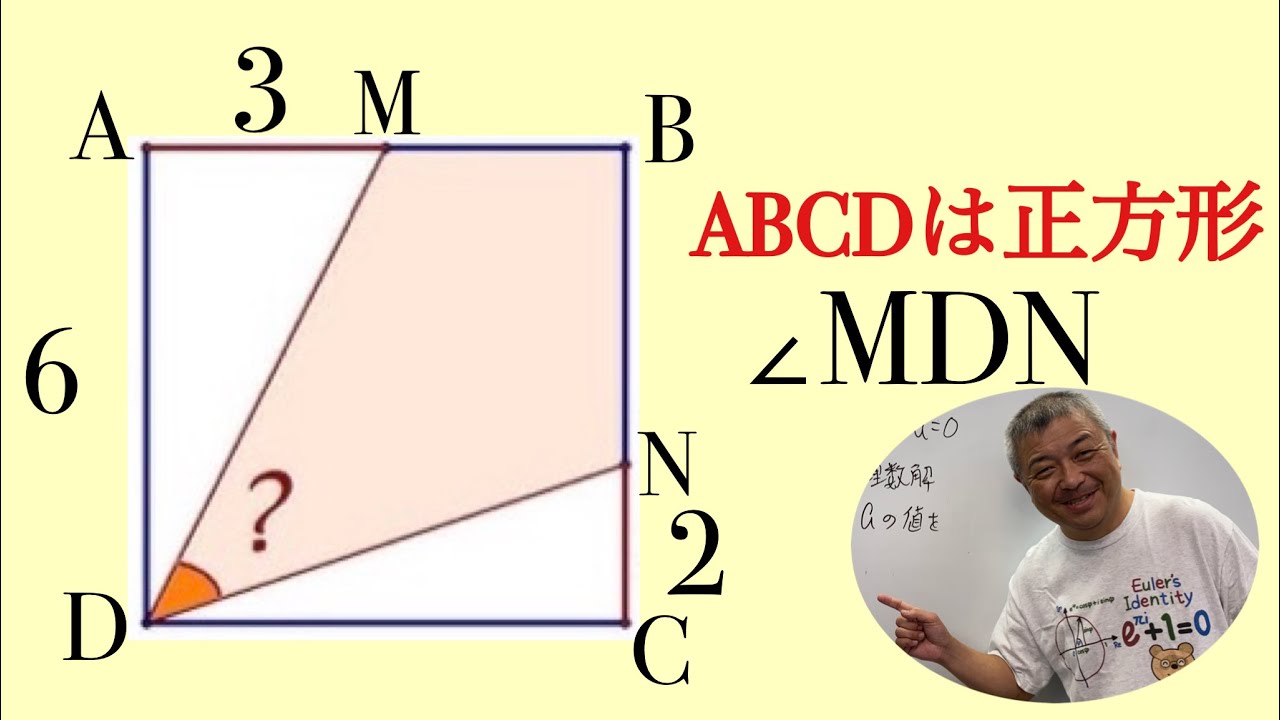
全米をsin撼させた問題です。
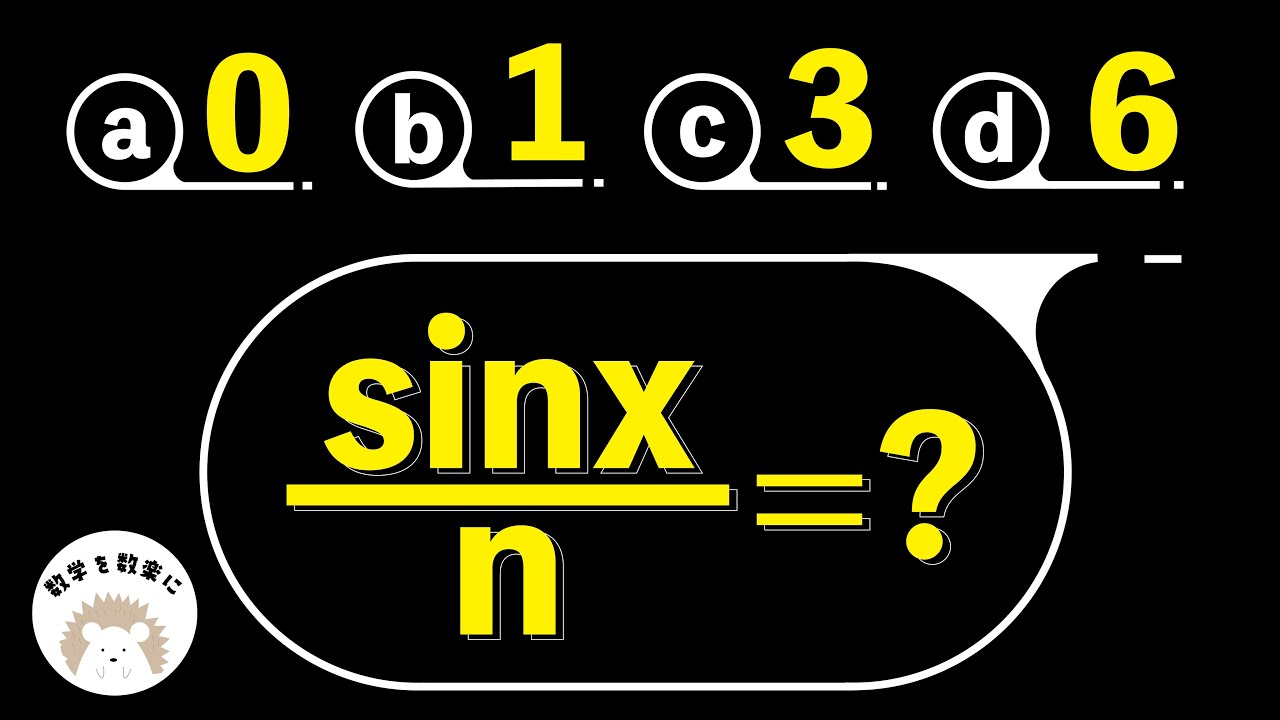
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{sinx}{n} = ?$
(a) 0
(b) 1
(c) 3
(d) 6
この動画を見る
$\frac{sinx}{n} = ?$
(a) 0
(b) 1
(c) 3
(d) 6
福田の共通テスト直前演習〜2021年共通テスト数学IA問題1[2]。三角比に関する問題。

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$[2]右の図のように、$\triangle ABC$の外側に辺AB,BC,CAをそれぞれ1辺とする
正方形ADEB,BFGC,CHIAをかき、2点EとF、GとH、IとDをそれぞれ
線分で結んだ図形を考える。以下において
$BC=a, CA=b, AB=c$
$\angle CAB=A, \angle ABC=B, \angle BCA=C$ とする。
(1)$b=6, c=5, \cos A=\frac{3}{5}$のとき、$\sin A=\frac{\boxed{セ}}{\boxed{ソ}}$であり、
$\triangle ABC$の面積は$\boxed{タチ}$、$\triangle AID$の面積は$\boxed{ツテ}$である。
(2)正方形BFGC,CHIA,ADEBの面積をそれぞれS_1,S_2,S_3とする。
このとき、$S_1-S_2-S_3$ は
・$0° \lt A \lt 90°$のとき$\boxed{ト}$ ・$A=90°$のとき$\boxed{ナ}$
・$90° \lt A \lt 180°$のとき$\boxed{ニ}$
$\boxed{ト}~\boxed{ニ}$の解答群
⓪0である ①正の値である ②負の値である ③正の値も負の値もとる
(3)$\triangle AID,\triangle BEF,\triangle CGH$の面積をそれぞれ$T_1,T_2,T_3$とする。
このとき、$\boxed{ヌ}$である。
$\boxed{ヌ}$の解答群
⓪$a \lt b \lt c$ならば$T_1 \gt T_2 \gt T_3$
①$a \lt b \lt c$ならば$T_1 \lt T_2 \lt T_3$
②Aが鈍角ならば$T_1 \lt T_2$ かつ$T_1 \lt T_3$
③$a,b,c$の値に関係なく、$T_1 = T_2 = T_3$
(4)$\triangle ABC,\triangle AID,\triangle BEF,\triangle CGH$のうち、外接円の半径が最も小さいもの
を求める。$0° \lt A \lt 90°$のとき、$ID \boxed{ネ} BC$であり、
$(\triangle AID$の外接円の半径)$\boxed{ノ}(\triangle ABCの外接円の半径)$
であるから、外接円の半径が最も小さい三角形は
$0° \lt A \lt B \lt C \lt 90°$のとき、$\boxed{ハ}$である。
$0° \lt A \lt B \lt 90° \lt C$のとき、$\boxed{ヒ}$である。
$\boxed{ネ}、\boxed{ノ}$の解答群
⓪$\lt$ ①$=$ ②$\gt$
$\boxed{ハ}、\boxed{ヒ}$の解答群
⓪$\triangle ABC$ ①$\triangle AID$ ②$\triangle BEF$ ③$\triangle CGH$
2021共通テスト数学過去問
この動画を見る
${\Large\boxed{1}}$[2]右の図のように、$\triangle ABC$の外側に辺AB,BC,CAをそれぞれ1辺とする
正方形ADEB,BFGC,CHIAをかき、2点EとF、GとH、IとDをそれぞれ
線分で結んだ図形を考える。以下において
$BC=a, CA=b, AB=c$
$\angle CAB=A, \angle ABC=B, \angle BCA=C$ とする。
(1)$b=6, c=5, \cos A=\frac{3}{5}$のとき、$\sin A=\frac{\boxed{セ}}{\boxed{ソ}}$であり、
$\triangle ABC$の面積は$\boxed{タチ}$、$\triangle AID$の面積は$\boxed{ツテ}$である。
(2)正方形BFGC,CHIA,ADEBの面積をそれぞれS_1,S_2,S_3とする。
このとき、$S_1-S_2-S_3$ は
・$0° \lt A \lt 90°$のとき$\boxed{ト}$ ・$A=90°$のとき$\boxed{ナ}$
・$90° \lt A \lt 180°$のとき$\boxed{ニ}$
$\boxed{ト}~\boxed{ニ}$の解答群
⓪0である ①正の値である ②負の値である ③正の値も負の値もとる
(3)$\triangle AID,\triangle BEF,\triangle CGH$の面積をそれぞれ$T_1,T_2,T_3$とする。
このとき、$\boxed{ヌ}$である。
$\boxed{ヌ}$の解答群
⓪$a \lt b \lt c$ならば$T_1 \gt T_2 \gt T_3$
①$a \lt b \lt c$ならば$T_1 \lt T_2 \lt T_3$
②Aが鈍角ならば$T_1 \lt T_2$ かつ$T_1 \lt T_3$
③$a,b,c$の値に関係なく、$T_1 = T_2 = T_3$
(4)$\triangle ABC,\triangle AID,\triangle BEF,\triangle CGH$のうち、外接円の半径が最も小さいもの
を求める。$0° \lt A \lt 90°$のとき、$ID \boxed{ネ} BC$であり、
$(\triangle AID$の外接円の半径)$\boxed{ノ}(\triangle ABCの外接円の半径)$
であるから、外接円の半径が最も小さい三角形は
$0° \lt A \lt B \lt C \lt 90°$のとき、$\boxed{ハ}$である。
$0° \lt A \lt B \lt 90° \lt C$のとき、$\boxed{ヒ}$である。
$\boxed{ネ}、\boxed{ノ}$の解答群
⓪$\lt$ ①$=$ ②$\gt$
$\boxed{ハ}、\boxed{ヒ}$の解答群
⓪$\triangle ABC$ ①$\triangle AID$ ②$\triangle BEF$ ③$\triangle CGH$
2021共通テスト数学過去問
【数Ⅰ】図形と計量:正四面体の体積を一瞬で求める方法

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【中学数学 三平方の定理 立体図形】
1辺の長さがaの正四面体の体積を求めよ
この動画を見る
【中学数学 三平方の定理 立体図形】
1辺の長さがaの正四面体の体積を求めよ
【数Ⅰ】三角比総まとめ【三角比の基本をざっくりと振り返ろう】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
三角比の基本に関して解説していきます.
この動画を見る
三角比の基本に関して解説していきます.
【数Ⅰ】円に内接する四角形【余弦定理を使い倒せ!】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 四角形ABCDは円に内接しており,AB=2,BC=4,CD=3,DA=3である.
(1)cosA,BDの長さを求めよ.
(2)四角形ABCDの面積を求めよ.$
この動画を見る
$ 四角形ABCDは円に内接しており,AB=2,BC=4,CD=3,DA=3である.
(1)cosA,BDの長さを求めよ.
(2)四角形ABCDの面積を求めよ.$
【数Ⅰ】面積公式・ヘロンの公式・内接円の半径【小学生からの脱却!】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
面積公式・ヘロンの公式・内接円の半径に関して解説していきます.
この動画を見る
面積公式・ヘロンの公式・内接円の半径に関して解説していきます.
【数Ⅰ】正弦定理・余弦定理の使い方【定理のキモチ】

福田のわかった数学〜高校1年生061〜三角形の形状決定問題(2)

単元:
#数Ⅰ#数Ⅱ#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形の形状決定(2)
次の等式が成り立つとき、$\triangle ABC$はどんな形の三角形か。
$\sin A\cos A=\sin B\cos B$
この動画を見る
数学$\textrm{I}$ 三角形の形状決定(2)
次の等式が成り立つとき、$\triangle ABC$はどんな形の三角形か。
$\sin A\cos A=\sin B\cos B$
福田のわかった数学〜高校1年生060〜三角形の形状決定問題(1)

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$三角形の形状決定(1)
次の等式が成り立つとき、$\triangle ABC$はどんな三角形か。
$a^2+b^2+c^2=bc(\frac{1}{2}+\cos A)+ca(\frac{1}{2}+\cos B)+ab(\frac{1}{2}+\cos C)$
この動画を見る
数学$\textrm{I}$三角形の形状決定(1)
次の等式が成り立つとき、$\triangle ABC$はどんな三角形か。
$a^2+b^2+c^2=bc(\frac{1}{2}+\cos A)+ca(\frac{1}{2}+\cos B)+ab(\frac{1}{2}+\cos C)$
福田のわかった数学〜高校1年生059〜図形の計量(10)正四面体の各辺に接する球の半径

単元:
#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(10)
1辺の長さがaの正四面体の全ての辺に接する球の半径を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(10)
1辺の長さがaの正四面体の全ての辺に接する球の半径を求めよ。
