 三角比への応用(正弦・余弦・面積)
三角比への応用(正弦・余弦・面積)
 三角比への応用(正弦・余弦・面積)
三角比への応用(正弦・余弦・面積)
福田のわかった数学〜高校1年生057〜図形の計量(8)正四面体の内接球の半径

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(8)
1辺の長さがaの正四面体の各面に接する内接球の半径を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(8)
1辺の長さがaの正四面体の各面に接する内接球の半径を求めよ。
別に積分しろとは言ってません。(広陵(改))
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
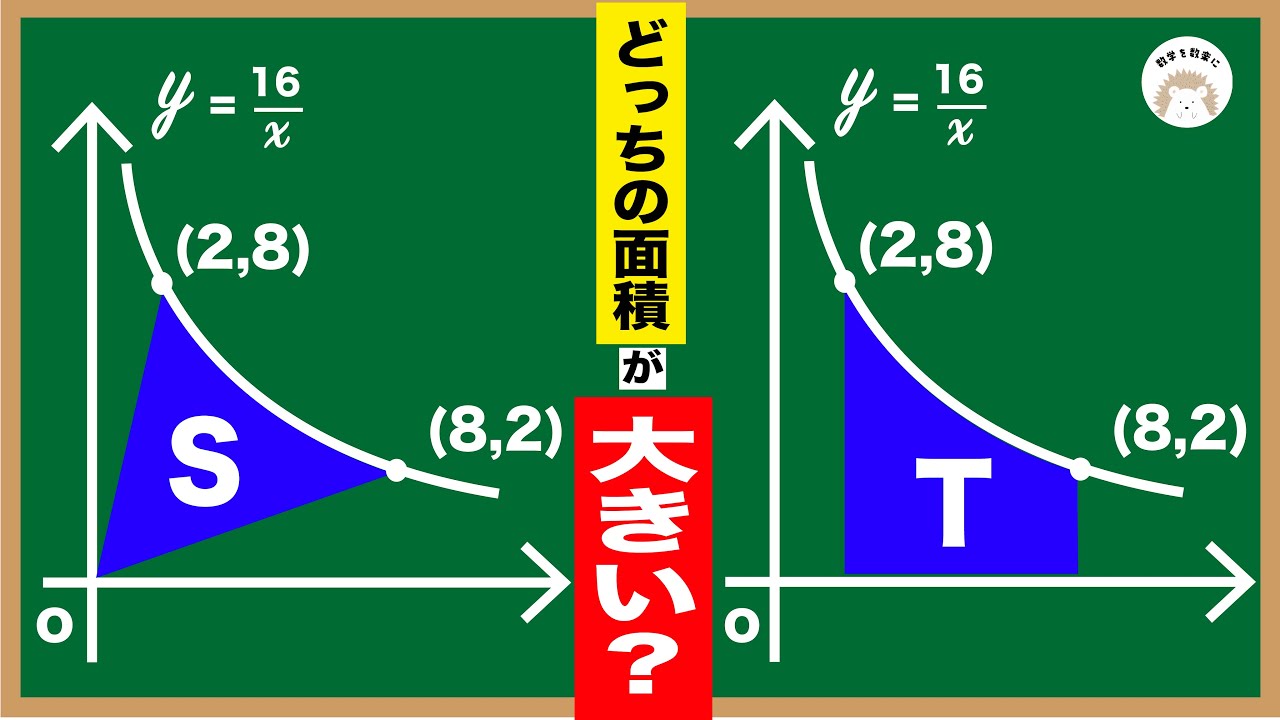
SとTどっちの面積が大きい?
*図は動画内参照
広陵高等学校
この動画を見る
SとTどっちの面積が大きい?
*図は動画内参照
広陵高等学校
福田のわかった数学〜高校1年生056〜図形の計量(7)等面四面体の体積

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(7)
4つの面のどれも3辺の長さが
5,6,7の三角形である四面体
(等面四面体)の体積を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(7)
4つの面のどれも3辺の長さが
5,6,7の三角形である四面体
(等面四面体)の体積を求めよ。
解けそうで解けない三角形の面積 城北
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
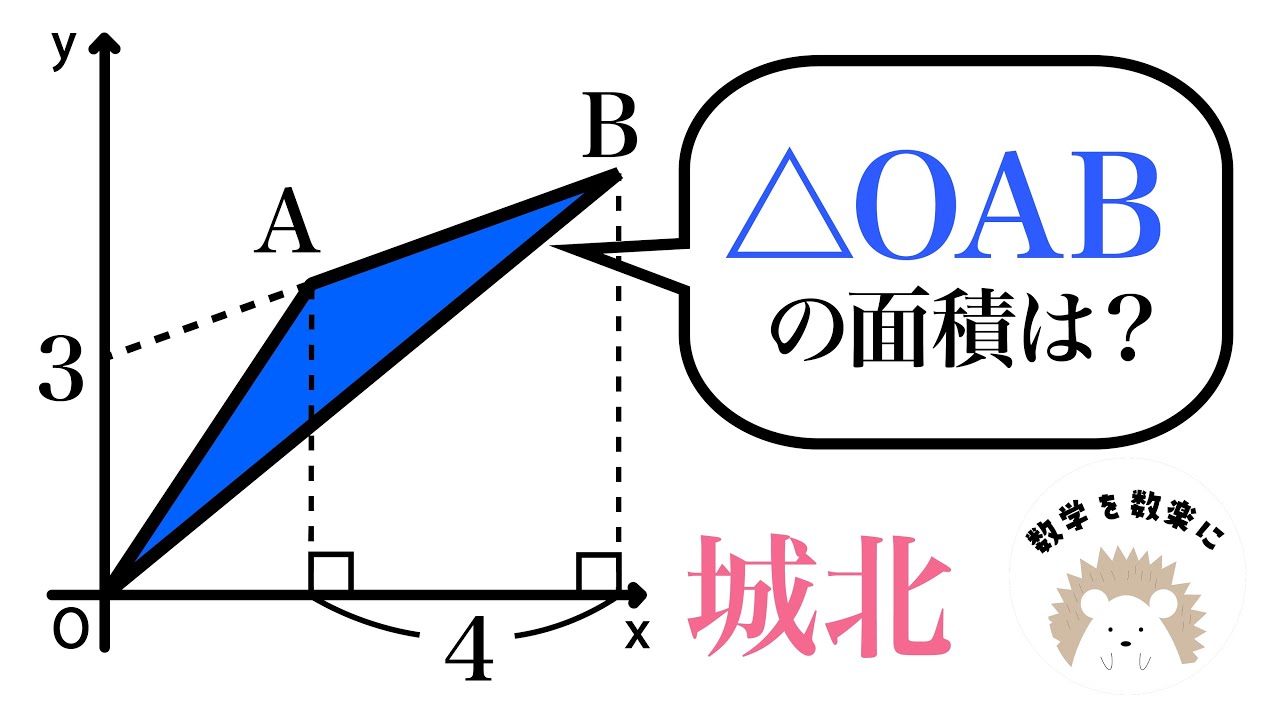
△OAB=?
*図は動画内参照
城北高等学校
この動画を見る
△OAB=?
*図は動画内参照
城北高等学校
福田のわかった数学〜高校1年生055〜図形の計量(6)正四面体の体積

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(6)
一辺の長さがaの正四面体の体積を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(6)
一辺の長さがaの正四面体の体積を求めよ。
福田のわかった数学〜高校1年生054〜図形の計量(5)四面体の体積(1)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(5)
四面体ABCDについて、
$AB=8,\ BC=4,\ CD=5,\ DA=8,\ BD=6,\ AC=8$
のとき体積を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(5)
四面体ABCDについて、
$AB=8,\ BC=4,\ CD=5,\ DA=8,\ BD=6,\ AC=8$
のとき体積を求めよ。
福田のわかった数学〜高校1年生053〜図形の計量(4)三角形の成立条件と最大角

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(4)
三辺の長さが$x^2+x+1, -2x-1, x^2+2x$である三角形の最大角を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(4)
三辺の長さが$x^2+x+1, -2x-1, x^2+2x$である三角形の最大角を求めよ。
福田のわかった数学〜高校1年生052〜図形の計量(3)台形の対角線のなす角
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
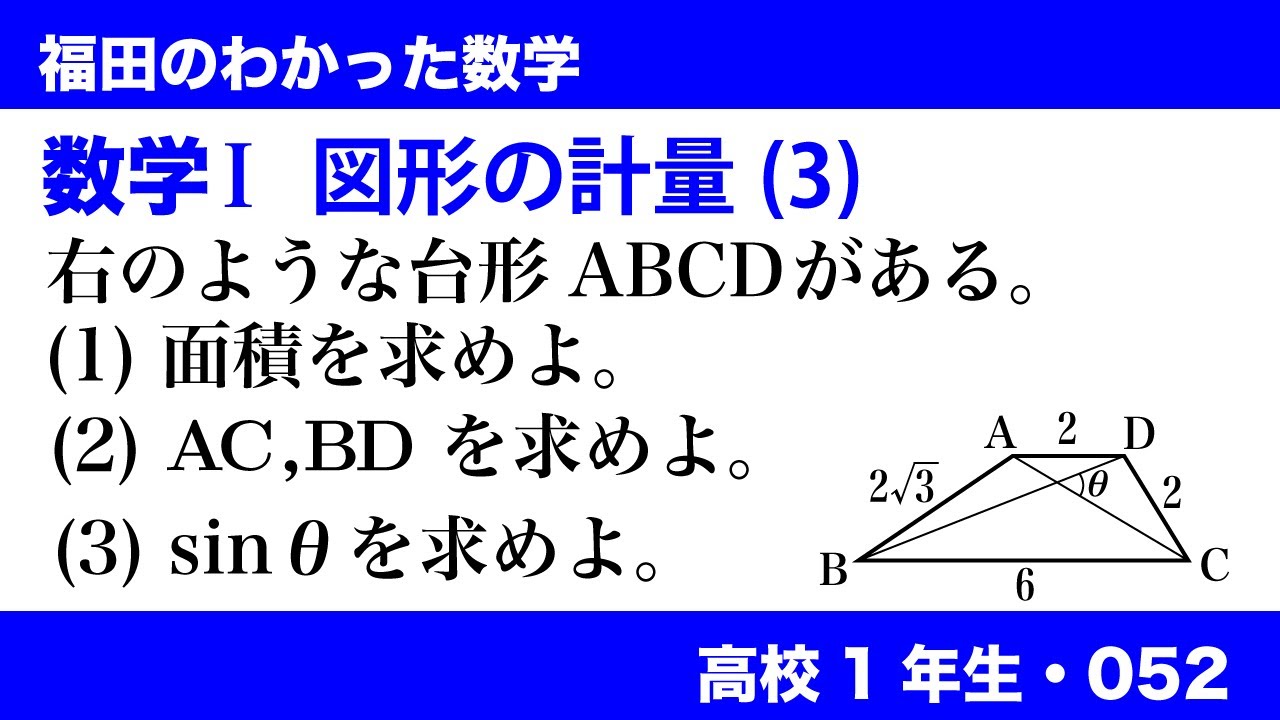
数学$\textrm{I}$ 図形の計量(3)
右のような台形ABCDがある。(※動画参照)
(1)面積を求めよ。
(2)AC,BDを求めよ。
(3)$\sin\theta$を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(3)
右のような台形ABCDがある。(※動画参照)
(1)面積を求めよ。
(2)AC,BDを求めよ。
(3)$\sin\theta$を求めよ。
福田のわかった数学〜高校1年生051〜図形の計量(2)四角形の対角線と面積
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
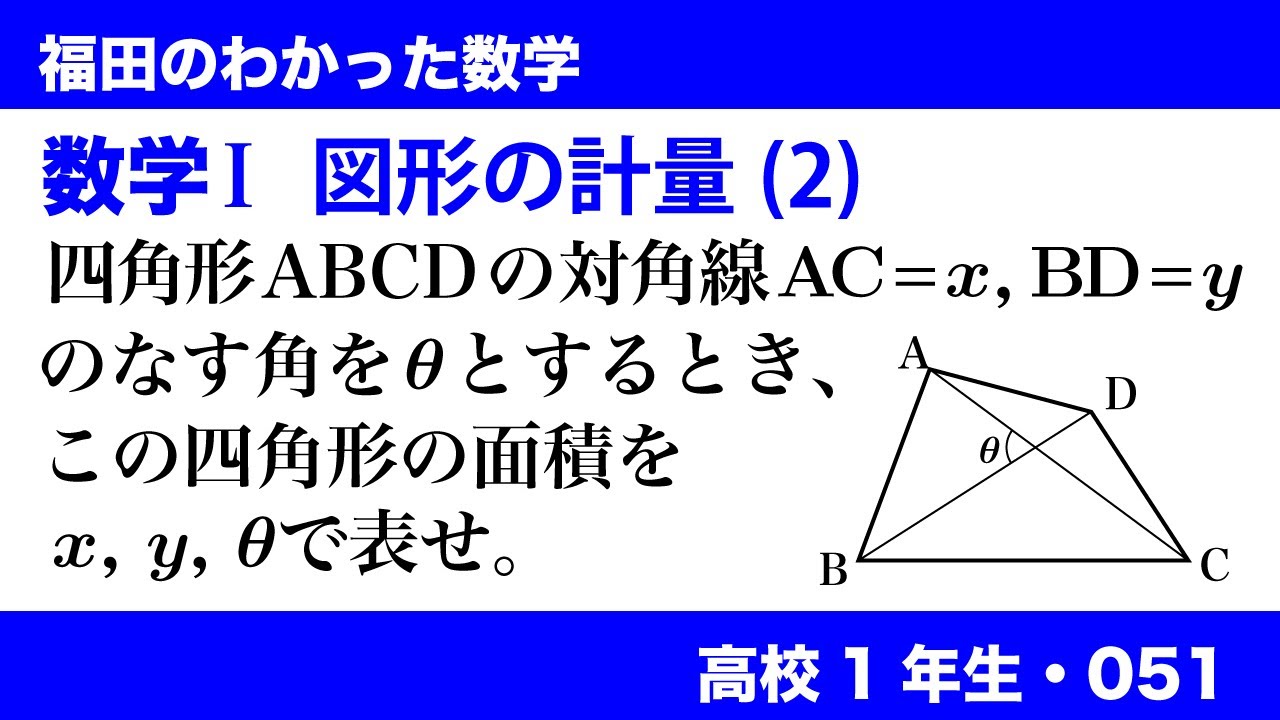
数学$\textrm{I}$図形の計量(2)
四角形ABCDの対角線$AC=x,\ BD=y$のなす角を$\theta$とするとき、
この四角形の面積を$x,\ y,\ \theta$で表せ。
この動画を見る
数学$\textrm{I}$図形の計量(2)
四角形ABCDの対角線$AC=x,\ BD=y$のなす角を$\theta$とするとき、
この四角形の面積を$x,\ y,\ \theta$で表せ。
【三角比 総まとめ!】三角比で必要な知識を「全て」まとめて解説!〔高校数学 数学〕

単元:
#数Ⅰ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
三角比で必要な知識を全てまとめました。
この動画を見る
三角比で必要な知識を全てまとめました。
福田のわかった数学〜高校1年生050〜図形の計量(1)内接四角形の面積

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(1)
$AB=3,\ BC=5,\ CD=5,\ DA=6$である
円に内接する四角形ABCDにおいて、
ACの長さ、四角形ABCDの面積Sを求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(1)
$AB=3,\ BC=5,\ CD=5,\ DA=6$である
円に内接する四角形ABCDにおいて、
ACの長さ、四角形ABCDの面積Sを求めよ。
大阪桐蔭 角の和

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
赤の角の和は何度?
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
赤の角の和は何度?
*図は動画内参照
大阪桐蔭高等学校
福田のわかった数学〜高校1年生049〜三角形への応用(6)正弦定理の捉え方

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形への応用(6)
$\triangle ABC$において、
$\sin A:\sin B:\sin C=3:5:7$
のとき、最も大きい角の大きさは?
この動画を見る
数学$\textrm{I}$ 三角形への応用(6)
$\triangle ABC$において、
$\sin A:\sin B:\sin C=3:5:7$
のとき、最も大きい角の大きさは?
福田のわかった数学〜高校1年生048〜三角形への応用(5)三角形を解く

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形への応用(5)
$\triangle ABC$において、$a=2,\ b=2\sqrt2,\ A=30°$
のとき、残りの辺と角の大きさを求めよ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(5)
$\triangle ABC$において、$a=2,\ b=2\sqrt2,\ A=30°$
のとき、残りの辺と角の大きさを求めよ。
福田のわかった数学〜高校1年生第47回。三角形への応用(4)内心
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
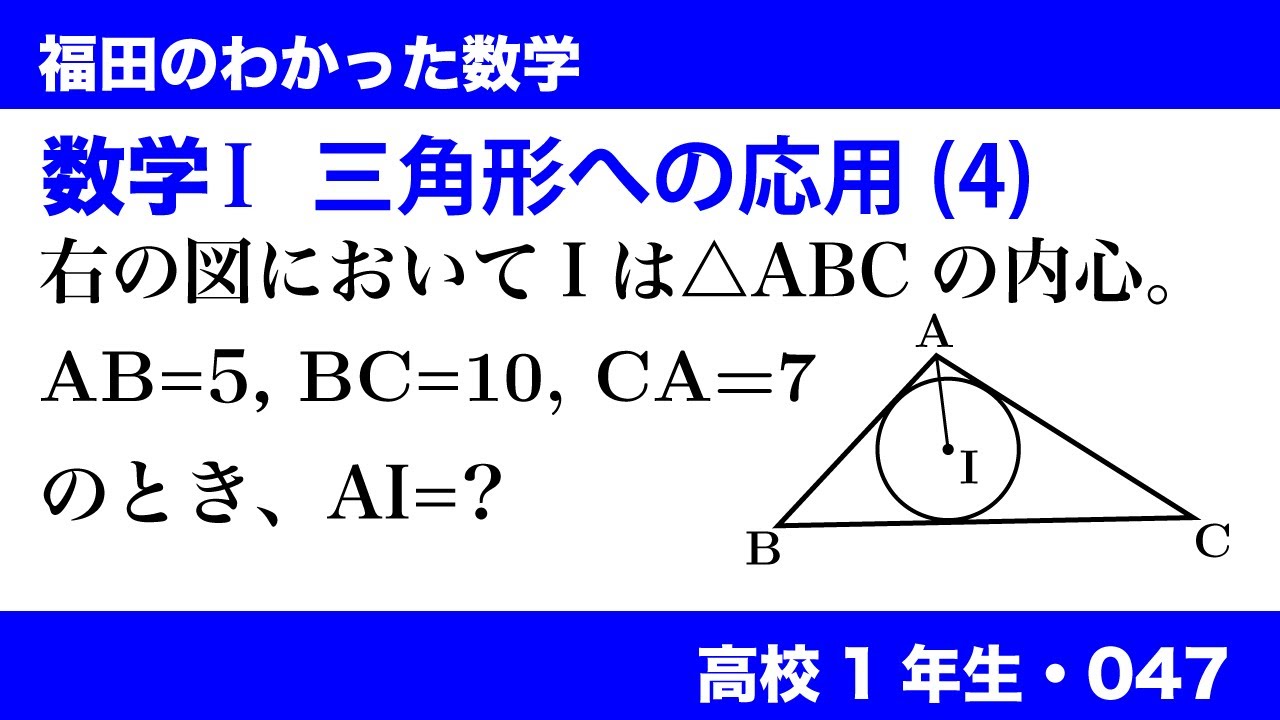
右の図において$I$は$\triangle ABC$の内心.$AB=5,BC=10,CA=7$のとき,$AI=?$
この動画を見る
右の図において$I$は$\triangle ABC$の内心.$AB=5,BC=10,CA=7$のとき,$AI=?$
福田のわかった数学〜高校1年生047〜三角形への応用(4)内心に関する問題

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
定義に従って$f(x)=x^n$を微分せよ.($n$は自然数)
この動画を見る
定義に従って$f(x)=x^n$を微分せよ.($n$は自然数)
福田のわかった数学〜高校1年生046〜三角形への応用(3)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形への応用(3)
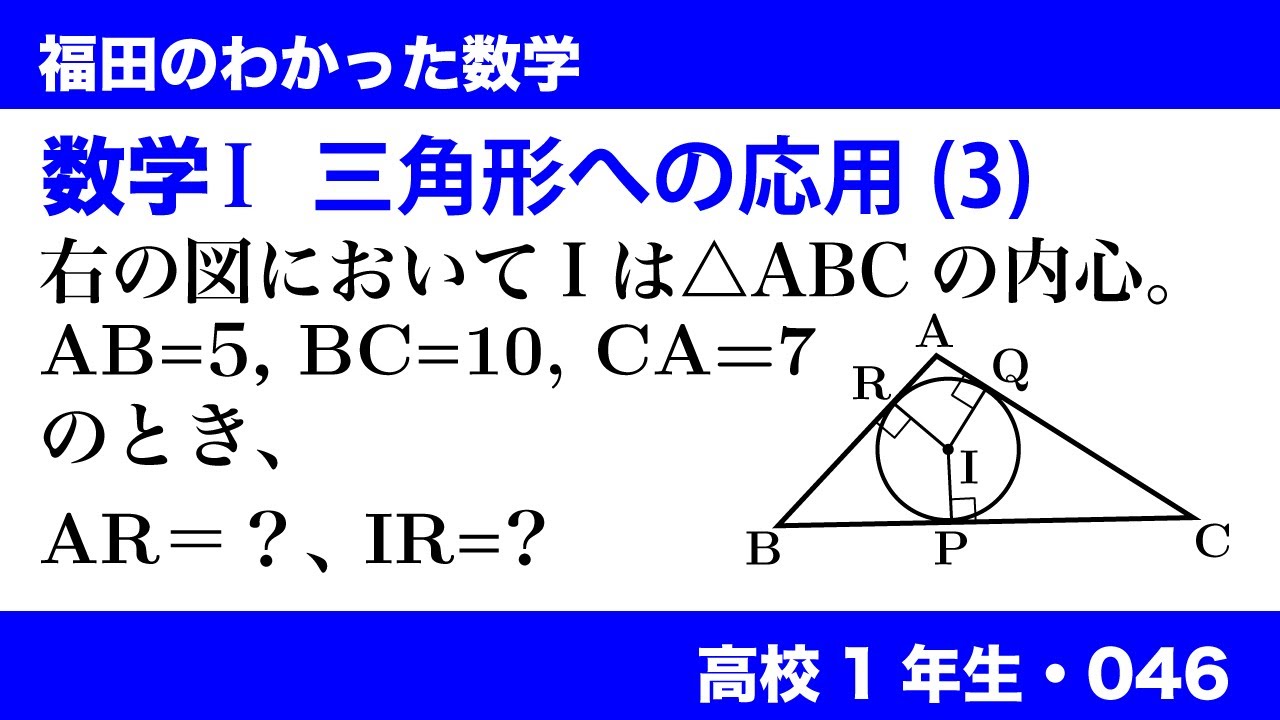
右の図(※動画参照)において、$I$は$\triangle ABC$の内心である。$AB=5,\ BC=10$
$CA=7$のとき、$AR,\ IR$を求めよ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(3)
右の図(※動画参照)において、$I$は$\triangle ABC$の内心である。$AB=5,\ BC=10$
$CA=7$のとき、$AR,\ IR$を求めよ。
【定理・公式の使い方を整理!】三角比の定理の使い方を総整理!〔高校数学 数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
1⃣
$\tan\theta=\sqrt{ 2 }$のとき、$\cos\theta$と$\sin\theta$を求めなさい($\theta$は鋭角)
2⃣
次の三角比を$90^{ \circ }$以下の角の三角比で表せ
(1)$\sin110^{ \circ }$
(2)$\cos120^{ \circ }$
(3)$\tan130^{ \circ }$
3⃣
動画内の図の$\triangle ABC$において$a$の長さを求め、面積も求めなさい
この動画を見る
1⃣
$\tan\theta=\sqrt{ 2 }$のとき、$\cos\theta$と$\sin\theta$を求めなさい($\theta$は鋭角)
2⃣
次の三角比を$90^{ \circ }$以下の角の三角比で表せ
(1)$\sin110^{ \circ }$
(2)$\cos120^{ \circ }$
(3)$\tan130^{ \circ }$
3⃣
動画内の図の$\triangle ABC$において$a$の長さを求め、面積も求めなさい
定理・公式の使い方を整理!】三角比の定理の使い方を総整理!〔高校数学 数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
1.$\tan θ=\sqrt{ 2 }$のとき、$\cosθ$と$sinθ$を求めなさい($θ$は鋭角)
2.次の三角比を$90^\circ$以下の角の三角比で表せ
(1)$sin110^\circ$ (2)$cos120^\circ$ (3)$tan130^\circ$
3.次の△ABCにおいて$a$の長さを求め、面積も求めなさい
※図は動画参照
この動画を見る
1.$\tan θ=\sqrt{ 2 }$のとき、$\cosθ$と$sinθ$を求めなさい($θ$は鋭角)
2.次の三角比を$90^\circ$以下の角の三角比で表せ
(1)$sin110^\circ$ (2)$cos120^\circ$ (3)$tan130^\circ$
3.次の△ABCにおいて$a$の長さを求め、面積も求めなさい
※図は動画参照
【数Ⅰ】高2生必見!!2020年度 第2回 K塾高2模試 大問2-2_図形と計量

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCにおいて、$AB=7、BC=8、CA=3$とする。
(1)$\cos\angle BAC$の値を求めよ。
(2)三角形ABCの面積を求めよ。
(3)三角形ABCの外接円において、点Aを含まない方の弧BC上に、$ \sin\angle BCP:\sin\angle CBP=1:3$となるように点Pをとる。
このとき、線分BPの長さと四角形 ABPCの面積を求めよ。
この動画を見る
三角形ABCにおいて、$AB=7、BC=8、CA=3$とする。
(1)$\cos\angle BAC$の値を求めよ。
(2)三角形ABCの面積を求めよ。
(3)三角形ABCの外接円において、点Aを含まない方の弧BC上に、$ \sin\angle BCP:\sin\angle CBP=1:3$となるように点Pをとる。
このとき、線分BPの長さと四角形 ABPCの面積を求めよ。
福田のわかった数学〜高校1年生045〜三角形への応用(2)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形への応用(2)
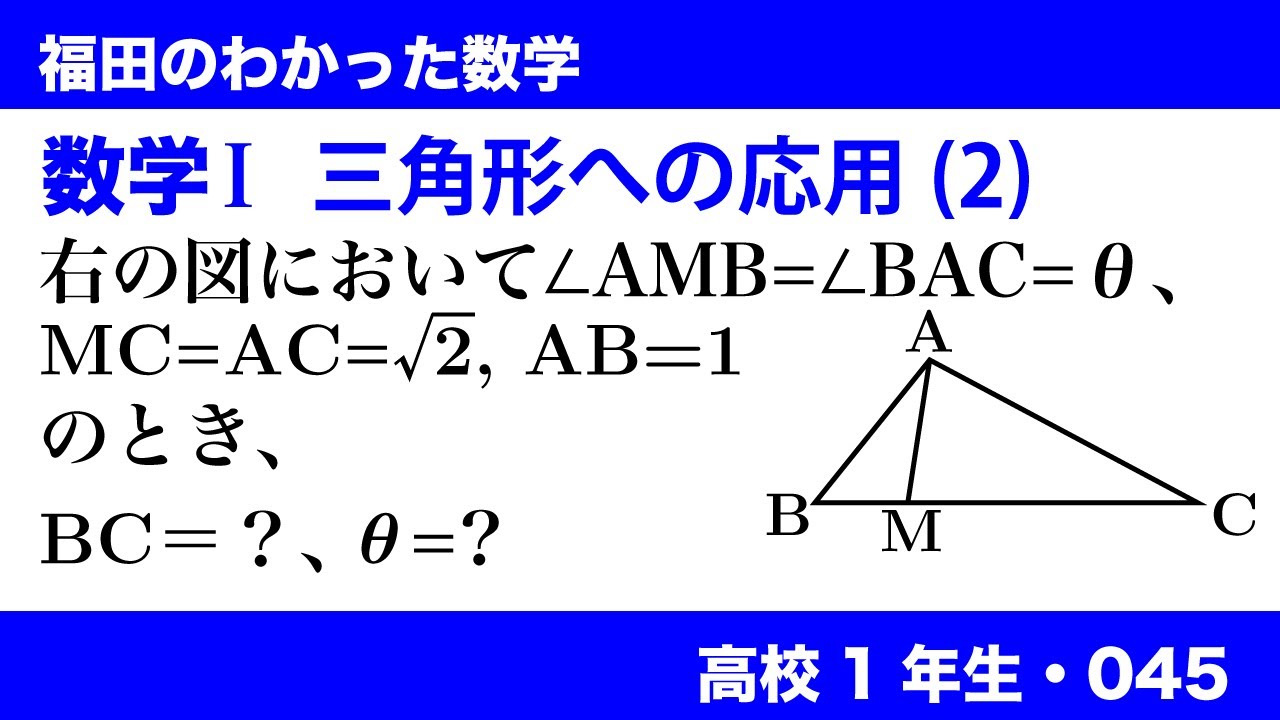
右の図(※動画参照)において$\angle AMB=\angle BAC=\theta$、
$MC=AC=\sqrt2, AB=1$のとき
$BC$を求め、$\theta$の値を求めよ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(2)
右の図(※動画参照)において$\angle AMB=\angle BAC=\theta$、
$MC=AC=\sqrt2, AB=1$のとき
$BC$を求め、$\theta$の値を求めよ。
【三角比の応用を整理!】三角比を使う定理の使い方を解説〔高校数学 数学〕

福田のわかった数学〜高校1年生044〜三角形への応用(1)正弦定理の証明

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形への応用(1)
三角形ABCの外接円の半径をRとする。
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
が成り立つことを示せ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(1)
三角形ABCの外接円の半径をRとする。
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
が成り立つことを示せ。
福田の数学〜慶應義塾大学2021年環境情報学部第1問〜三角形の内部にある外接している5つの円
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#方べきの定理と2つの円の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
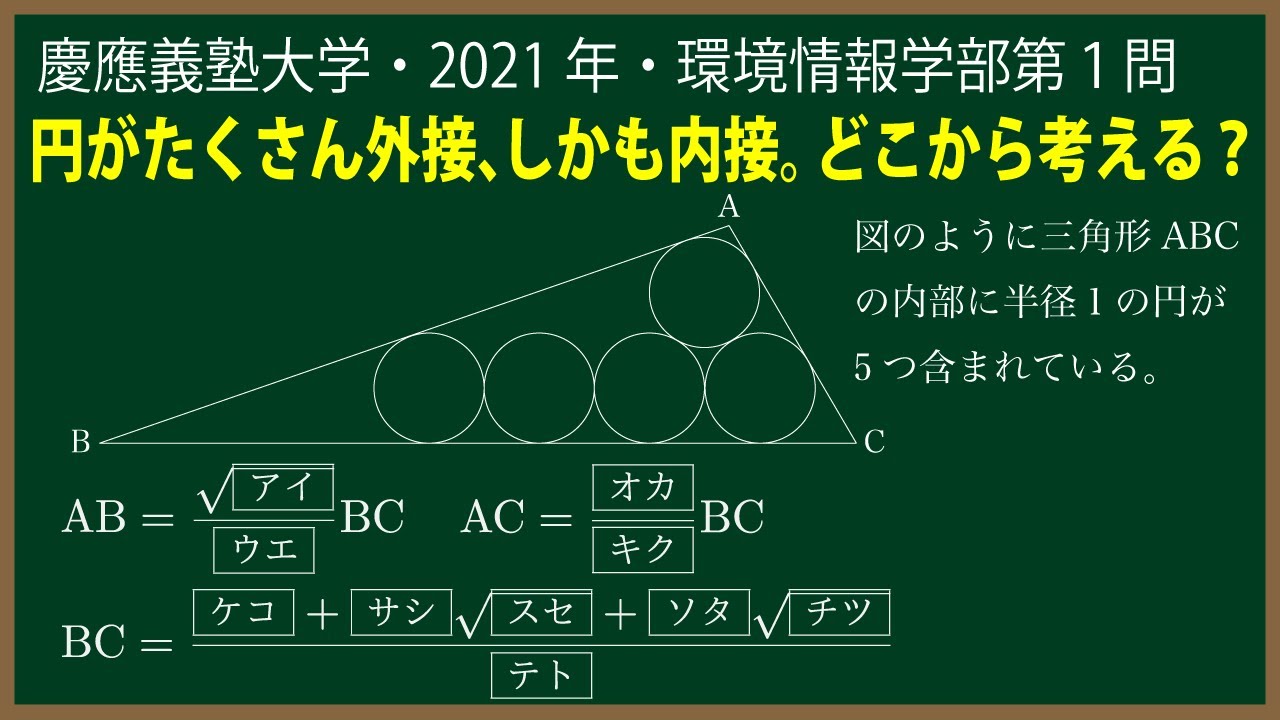
図(※動画参照)のように三角形$\rm ABC$の内部に半径$1$の円が5つ含まれている。4つの円は辺$\rm BC$に接しながら横一列に互いに接しながら並び、左端の円は辺$\rm AB$に接し、右端の円は辺$\rm AC$に接している。また、もう一つの円は、辺$\rm AB$と辺$\rm AC$に接し、4つの円の右側の2つの円に接している。このとき
$\textrm{AB}=\dfrac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\textrm{BC}$
$\rm AC=\dfrac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}BC$
$\rm BC=\dfrac{1}{\boxed{\ \ テト\ \ }}(\boxed{\ \ ケコ\ \ }+$$\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}+$$\boxed{\ \ ソタ\ \ }\sqrt{\boxed{\ \ チツ\ \ }})$ $(\boxed{\ \ スセ\ \ } \lt \boxed{\ \ チツ\ \ })$
である。
2021慶應義塾大学環境情報学部過去問
この動画を見る
${\Large\boxed{1}}$
図(※動画参照)のように三角形$\rm ABC$の内部に半径$1$の円が5つ含まれている。4つの円は辺$\rm BC$に接しながら横一列に互いに接しながら並び、左端の円は辺$\rm AB$に接し、右端の円は辺$\rm AC$に接している。また、もう一つの円は、辺$\rm AB$と辺$\rm AC$に接し、4つの円の右側の2つの円に接している。このとき
$\textrm{AB}=\dfrac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\textrm{BC}$
$\rm AC=\dfrac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}BC$
$\rm BC=\dfrac{1}{\boxed{\ \ テト\ \ }}(\boxed{\ \ ケコ\ \ }+$$\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}+$$\boxed{\ \ ソタ\ \ }\sqrt{\boxed{\ \ チツ\ \ }})$ $(\boxed{\ \ スセ\ \ } \lt \boxed{\ \ チツ\ \ })$
である。
2021慶應義塾大学環境情報学部過去問
補助線を引け!解説2通り
福田の数学〜早稲田大学2021年人間科学部第2問(2)〜3辺の長さから三角形の面積を求める

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(2)3辺の長さがそれぞれ$5,16,19$の三角形の面積は$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{2}}$
(2)3辺の長さがそれぞれ$5,16,19$の三角形の面積は$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$である。
2021早稲田大学人間科学部過去問
【高校数学】三角形の角の大きさと辺の長さの関係~余弦定理から分かる~ 3-7【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
余弦定理から分かる三角形の角の大きさと辺の長さの関係についての説明動画です
この動画を見る
余弦定理から分かる三角形の角の大きさと辺の長さの関係についての説明動画です
数学「大学入試良問集」【6−6 外接球と四面体】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
(1)$\angle BAC$を求めよ。
(2)$\triangle ABC$の外接円の半径を求めよ。
(3)4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
この動画を見る
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
(1)$\angle BAC$を求めよ。
(2)$\triangle ABC$の外接円の半径を求めよ。
(3)4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
【高校数学】余弦定理の証明~上級者向け~ 3-6.5【数学Ⅰ】

数学「大学入試良問集」【6−3 内接四角形】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
四角形$ABCD$が、半径$\displaystyle \frac{65}{8}$の円に内接している。
この四角形の週の長さが$44$で、辺$BC$と辺$CD$の長さがいずれも$13$であるとき、残りの2辺$AB$と$DA$の長さを求めよ。
この動画を見る
四角形$ABCD$が、半径$\displaystyle \frac{65}{8}$の円に内接している。
この四角形の週の長さが$44$で、辺$BC$と辺$CD$の長さがいずれも$13$であるとき、残りの2辺$AB$と$DA$の長さを求めよ。
