 図形と計量
図形と計量
 図形と計量
図形と計量
円と直角三角形 B
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
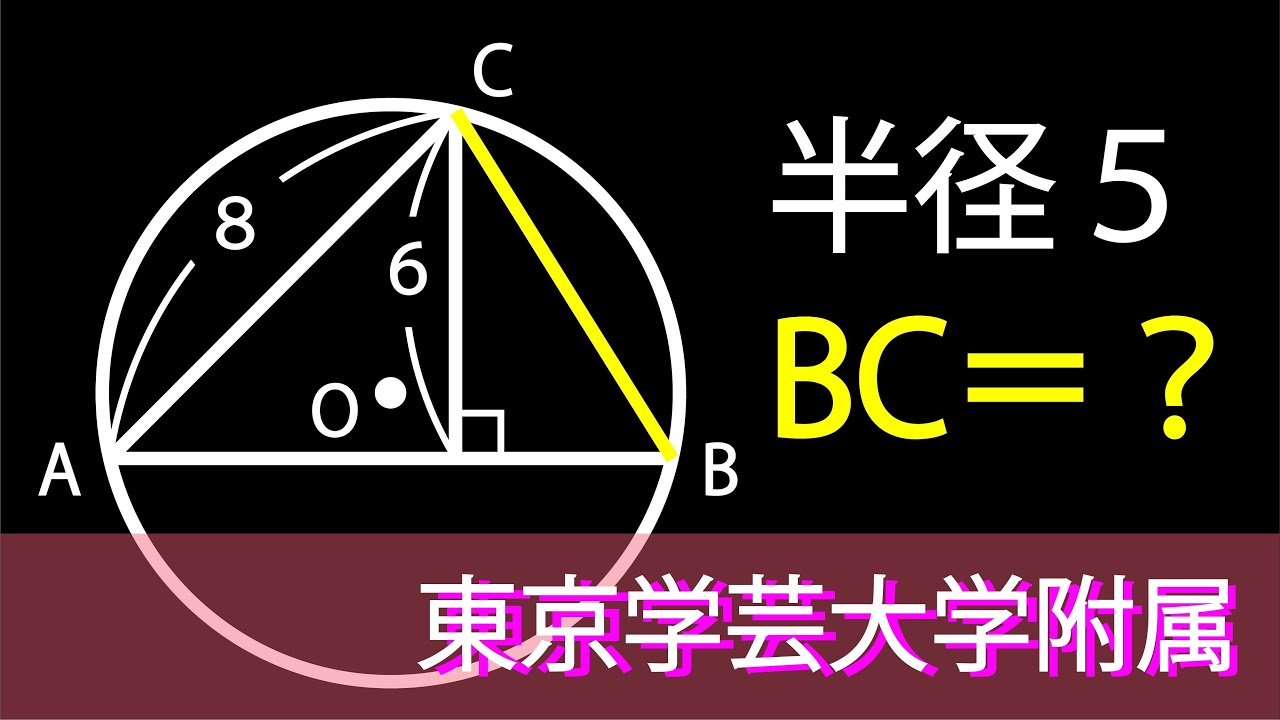
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
円 学芸大学附属 B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
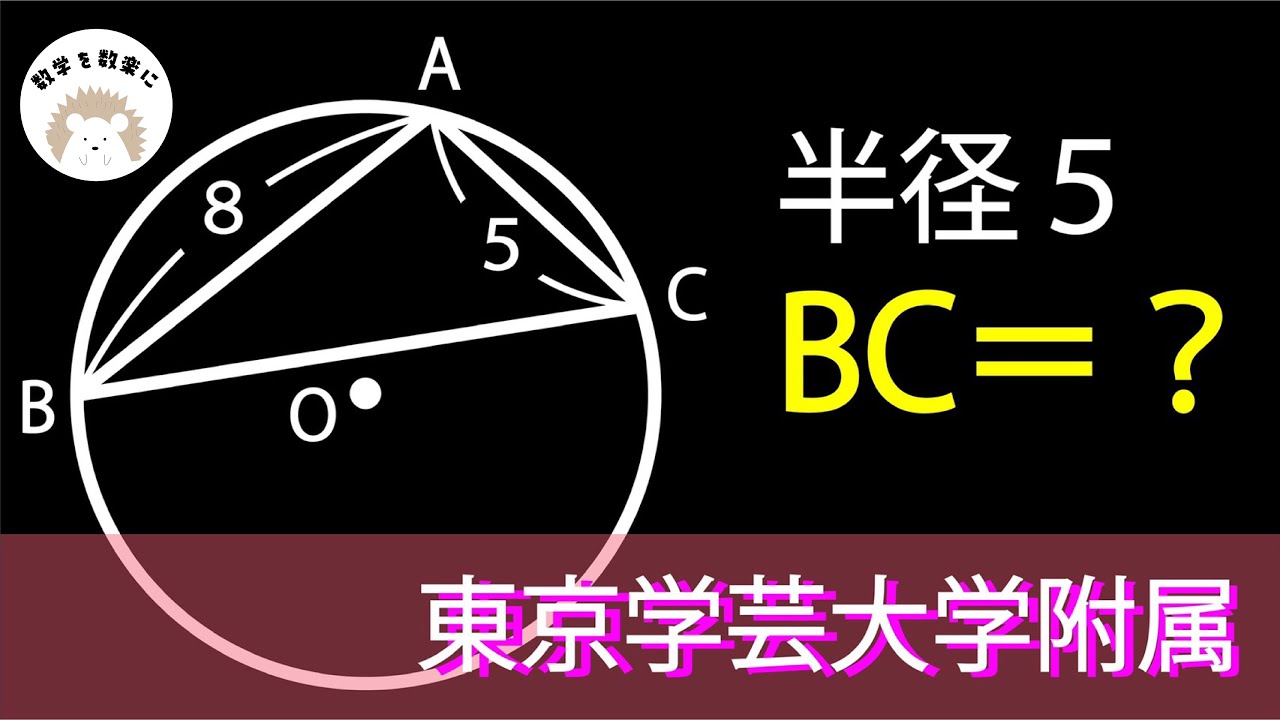
円の半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
円の半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
福田の数学〜早稲田大学2021年人間科学部第7問〜双曲線と図形問題

単元:
#数Ⅰ#大学入試過去問(数学)#平面上の曲線#図形と計量#2次曲線#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
補助線を引け!解説2通り
垂線の長さの和=❓ B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
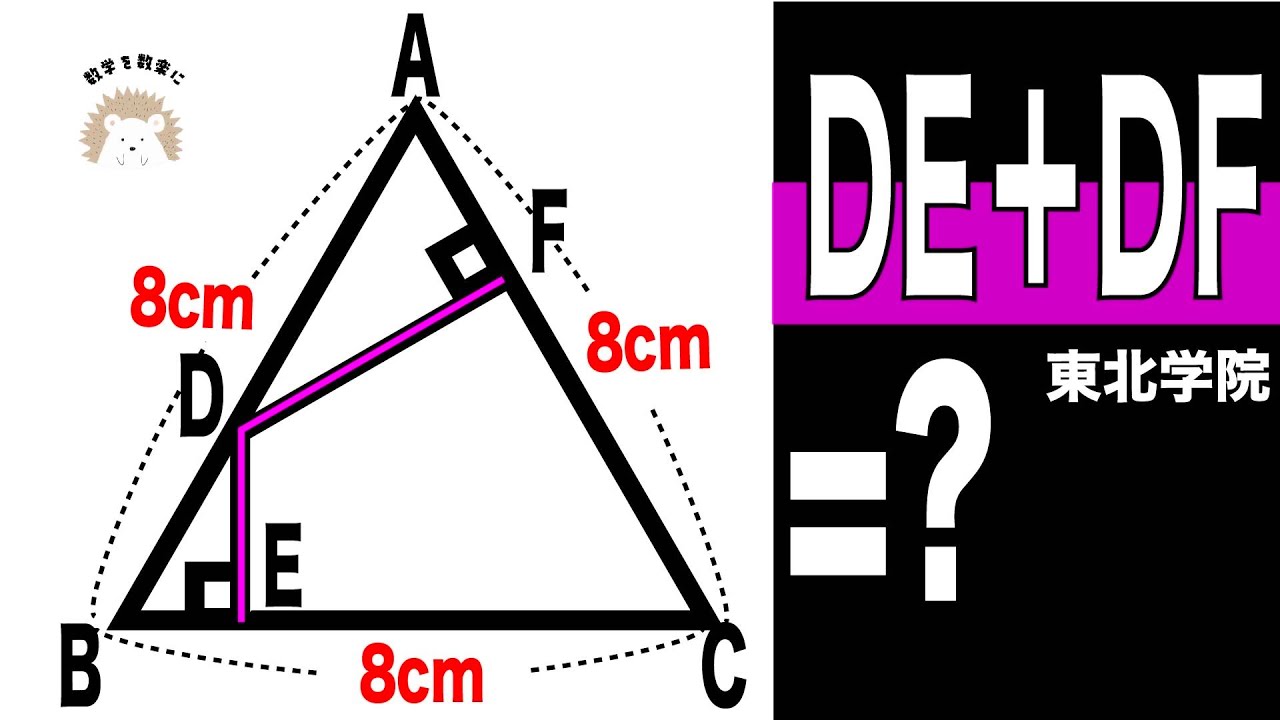
DE+EF=?
*図は動画内参照
東北学院高等学校
この動画を見る
DE+EF=?
*図は動画内参照
東北学院高等学校
福田の数学〜早稲田大学2021年人間科学部第2問(2)〜3辺の長さから三角形の面積を求める

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(2)3辺の長さがそれぞれ$5,16,19$の三角形の面積は$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{2}}$
(2)3辺の長さがそれぞれ$5,16,19$の三角形の面積は$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$である。
2021早稲田大学人間科学部過去問
【高校数学】三角関数の性質の考え方~θ+2nπ, -θ, θ+π, θ+π/2~ 4-3 【数学Ⅱ】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
たくさんある三角比の公式
覚えないといけないと思っていませんか!?
暗記は不要です!!
この動画を見る
たくさんある三角比の公式
覚えないといけないと思っていませんか!?
暗記は不要です!!
【数Ⅰ】図形と計量:三角比の表④演習 (1)sin60°(2)cos45°(3)tan120°(4)cos90°の値を求めよ。

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)sin60°(2)cos45°(3)tan120°(4)cos90°の値を求めよ。
この動画を見る
(1)sin60°(2)cos45°(3)tan120°(4)cos90°の値を求めよ。
【数Ⅰ】図形と計量:三角比の表③

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・sin0°, sin90°, sin180°の値を求めよ。
・cos0°, cos90°, cos180°の値を求めよ。
・tan0°, tan90°, tan180°の値を求めよ。
この動画を見る
・sin0°, sin90°, sin180°の値を求めよ。
・cos0°, cos90°, cos180°の値を求めよ。
・tan0°, tan90°, tan180°の値を求めよ。
早稲田実業高 円の性質・角の二等分線の定理
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
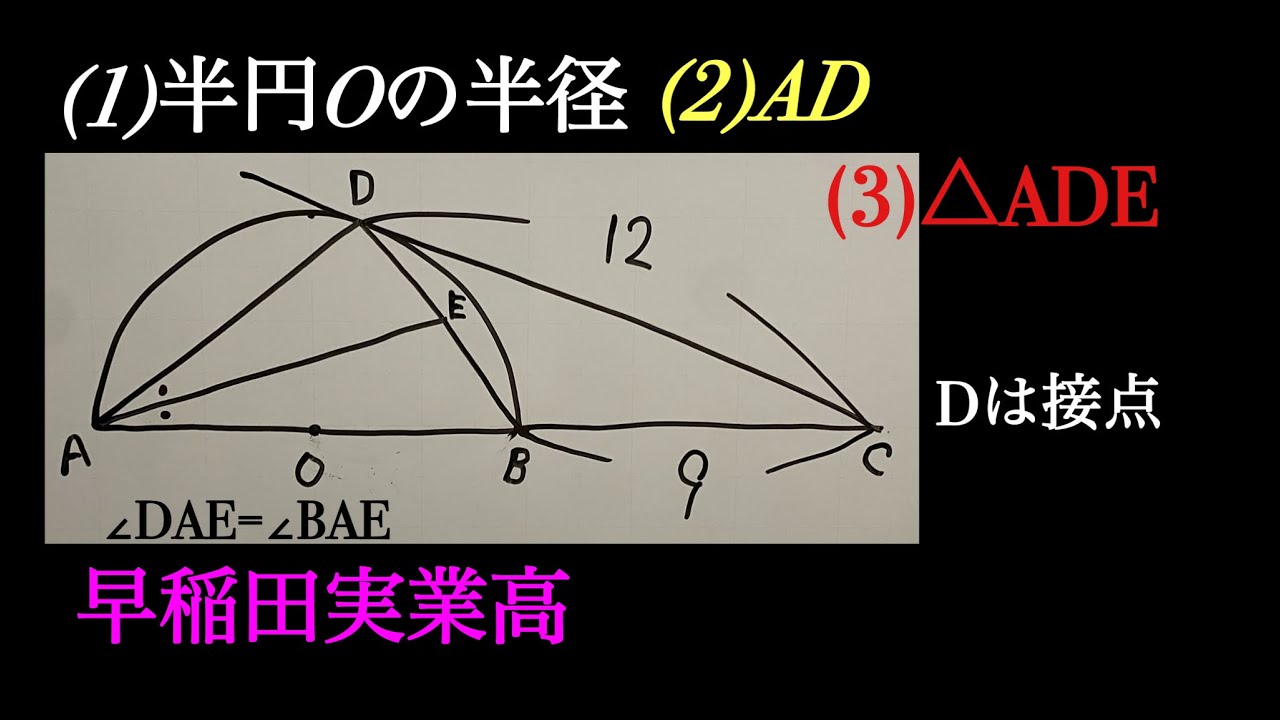
(1)半円の半径を求めよ.
(2)$AD$の長さを求めよ.
(3)$\triangle ADE$の長さを求めよ.
早稲田実業高過去問
この動画を見る
(1)半円の半径を求めよ.
(2)$AD$の長さを求めよ.
(3)$\triangle ADE$の長さを求めよ.
早稲田実業高過去問
【高校数学】弧度法を簡単に分かりやすく~ラジアンとは~ 4-1.5【数学Ⅱ】

角度 解けたら楽しい レベルC
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
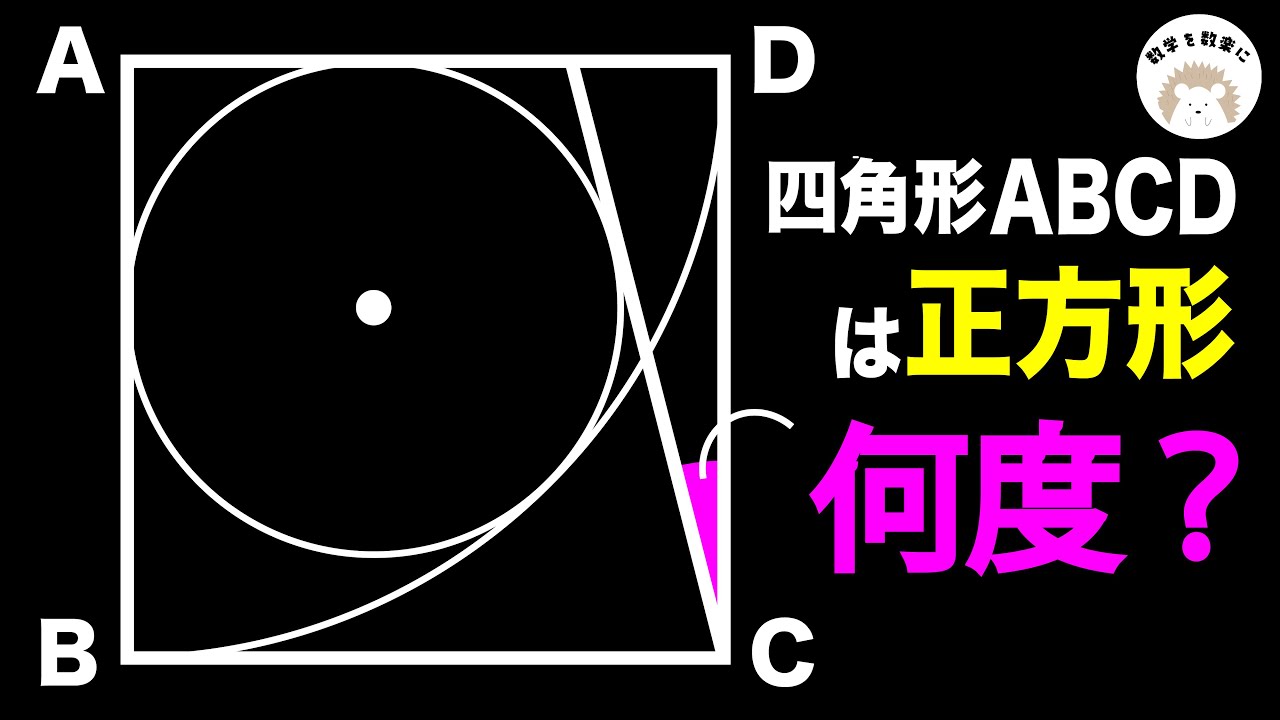
四角形ABCDは正方形
$\angle x=?$
*図は動画内参照
この動画を見る
四角形ABCDは正方形
$\angle x=?$
*図は動画内参照
【高校数学】三角形の角の大きさと辺の長さの関係~余弦定理から分かる~ 3-7【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
余弦定理から分かる三角形の角の大きさと辺の長さの関係についての説明動画です
この動画を見る
余弦定理から分かる三角形の角の大きさと辺の長さの関係についての説明動画です
【数Ⅰ】図形と計量:三角比の表②

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・sin120°, sin135°, sin150°の値を求めよ。
・cos120°, cos135°, cos150°の値を求めよ。
・tan120°, tan135°, tan150°の値を求めよ。
この動画を見る
・sin120°, sin135°, sin150°の値を求めよ。
・cos120°, cos135°, cos150°の値を求めよ。
・tan120°, tan135°, tan150°の値を求めよ。
【数Ⅰ】図形と計量:三角比の表①30°45°60°から!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・sin30°, sin45°, sin60°の値を求めよ。
・cos30°, cos45°, cos60°の値を求めよ。
・tan30°, tan45°, tan60°の値を求めよ。
この動画を見る
・sin30°, sin45°, sin60°の値を求めよ。
・cos30°, cos45°, cos60°の値を求めよ。
・tan30°, tan45°, tan60°の値を求めよ。
数学「大学入試良問集」【6−6 外接球と四面体】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
(1)$\angle BAC$を求めよ。
(2)$\triangle ABC$の外接円の半径を求めよ。
(3)4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
この動画を見る
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
(1)$\angle BAC$を求めよ。
(2)$\triangle ABC$の外接円の半径を求めよ。
(3)4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
数学「大学入試良問集」【6−5 母線の等しい四面体】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
1辺の長さが2の正三角形$ABC$を底面とし、
$OA=OB=OC=2a(a \gt 1)$
である四面体$OABC$について、辺$AB$の中点を$M$とし、頂点$O$から直線$CM$に下した垂線を$OH$とする。
$\angle OMC=\theta$とするとき、次の各問いに答えよ。
(1)$\cos\theta$を$a$を用いて表せ。
(2)$OH$の長さを$a$を用いて表せ。
(3)$OH$の長さが$2\sqrt{ 3 }$になるときの$a$の値を求めよ。
この動画を見る
1辺の長さが2の正三角形$ABC$を底面とし、
$OA=OB=OC=2a(a \gt 1)$
である四面体$OABC$について、辺$AB$の中点を$M$とし、頂点$O$から直線$CM$に下した垂線を$OH$とする。
$\angle OMC=\theta$とするとき、次の各問いに答えよ。
(1)$\cos\theta$を$a$を用いて表せ。
(2)$OH$の長さを$a$を用いて表せ。
(3)$OH$の長さが$2\sqrt{ 3 }$になるときの$a$の値を求めよ。
【高校数学】余弦定理の証明~上級者向け~ 3-6.5【数学Ⅰ】

数学「大学入試良問集」【6−3 内接四角形】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
四角形$ABCD$が、半径$\displaystyle \frac{65}{8}$の円に内接している。
この四角形の週の長さが$44$で、辺$BC$と辺$CD$の長さがいずれも$13$であるとき、残りの2辺$AB$と$DA$の長さを求めよ。
この動画を見る
四角形$ABCD$が、半径$\displaystyle \frac{65}{8}$の円に内接している。
この四角形の週の長さが$44$で、辺$BC$と辺$CD$の長さがいずれも$13$であるとき、残りの2辺$AB$と$DA$の長さを求めよ。
どっちがでかい?
数学「大学入試良問集」【6−2 隣接する内接円】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
3辺$AB,BC,CA$の長さがそれぞれ$7,6,5$の三角形$ABC$において、三角形$ABC$の面積を$S$、三角形$ABC$の内接円$I$のを半径$r$とする。
さらに、2辺$AB,BC$および内接円$I$に接する円の半径を$r_1$とし、半径$r_1$の円は、内接円$I$とは異なるものとする。
(1)$\cos\ B,\sin\displaystyle \frac{B}{2}$の値を求めよ。
(2)$S,r$の値を求めよ。
(3)$\sin\displaystyle \frac{B}{2}$を$r,r_1$を用いて表せ。
(4)$r_1$の値を求めよ。
この動画を見る
3辺$AB,BC,CA$の長さがそれぞれ$7,6,5$の三角形$ABC$において、三角形$ABC$の面積を$S$、三角形$ABC$の内接円$I$のを半径$r$とする。
さらに、2辺$AB,BC$および内接円$I$に接する円の半径を$r_1$とし、半径$r_1$の円は、内接円$I$とは異なるものとする。
(1)$\cos\ B,\sin\displaystyle \frac{B}{2}$の値を求めよ。
(2)$S,r$の値を求めよ。
(3)$\sin\displaystyle \frac{B}{2}$を$r,r_1$を用いて表せ。
(4)$r_1$の値を求めよ。
【高校数学】余弦定理~基礎事項と使い方の確認~ 3-6【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$\triangle ABC$において、$b=2,c=3,A=60^{ \circ }$のとき、$a$を求めよ。
2⃣
$\triangle ABC$において、$a=8,b=5,c=7$のとき、$C$を求めよ。
この動画を見る
1⃣
$\triangle ABC$において、$b=2,c=3,A=60^{ \circ }$のとき、$a$を求めよ。
2⃣
$\triangle ABC$において、$a=8,b=5,c=7$のとき、$C$を求めよ。
おうぎ形の折り返しB 中1も解ける!
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
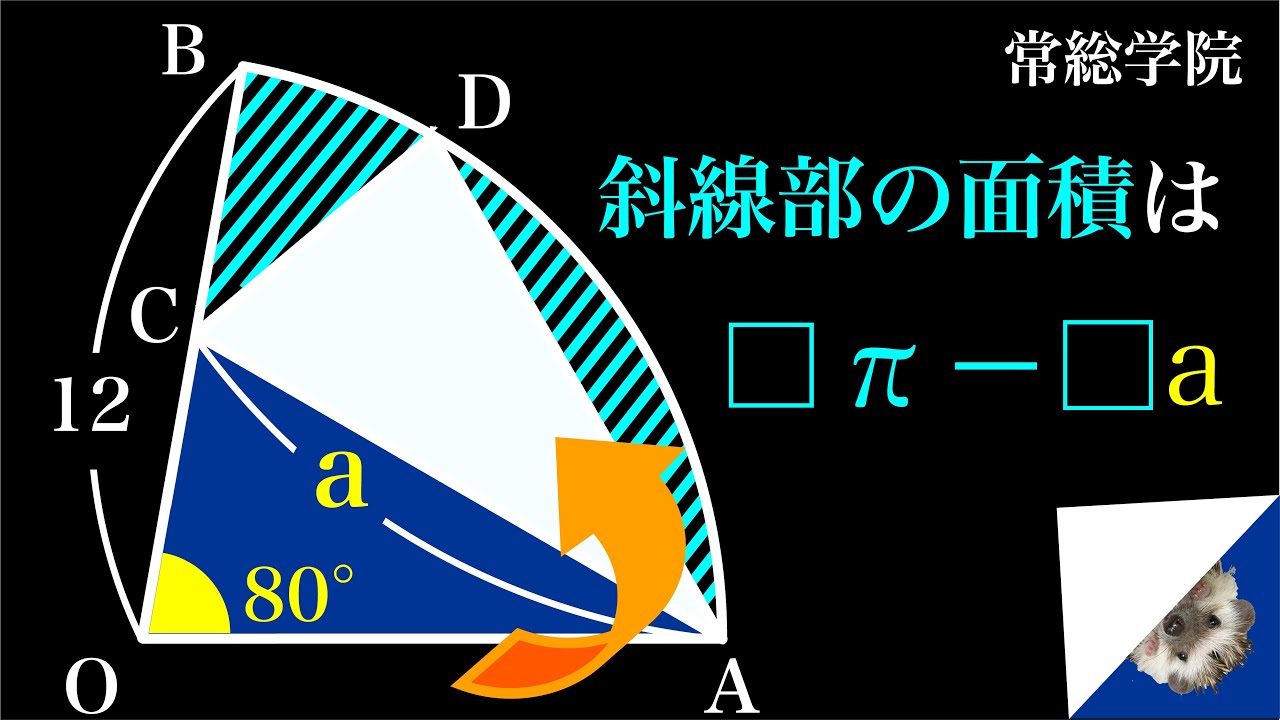
斜線部の面積=?
*図は動画内参照
この動画を見る
斜線部の面積=?
*図は動画内参照
【高校数学】正弦定理の証明~上級者向け~ 3-5.5【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【上級者向け】正弦定理の証明説明動画です
この動画を見る
【上級者向け】正弦定理の証明説明動画です
【高校数学】正弦定理~基礎事項と使い方の確認~ 3-5【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\triangle ABC$において、$a=10,B=60,C=70^{ \circ }$のとき、$b$を求めよ。
この動画を見る
$\triangle ABC$において、$a=10,B=60,C=70^{ \circ }$のとき、$b$を求めよ。
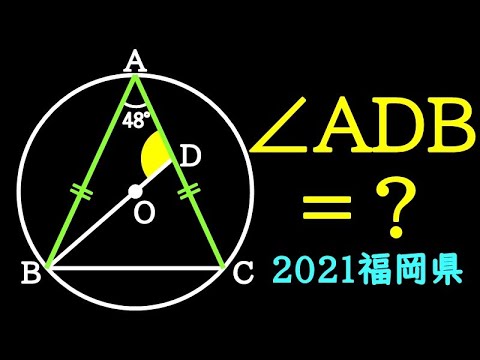
人生色々 補助線の引き方も色々(3通りの解説) A
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle ADB=?$
*図は動画内参照
2021福岡県
この動画を見る
$\angle ADB=?$
*図は動画内参照
2021福岡県
【正弦定理】超簡単な証明。式なしで証明できるwww【数学】
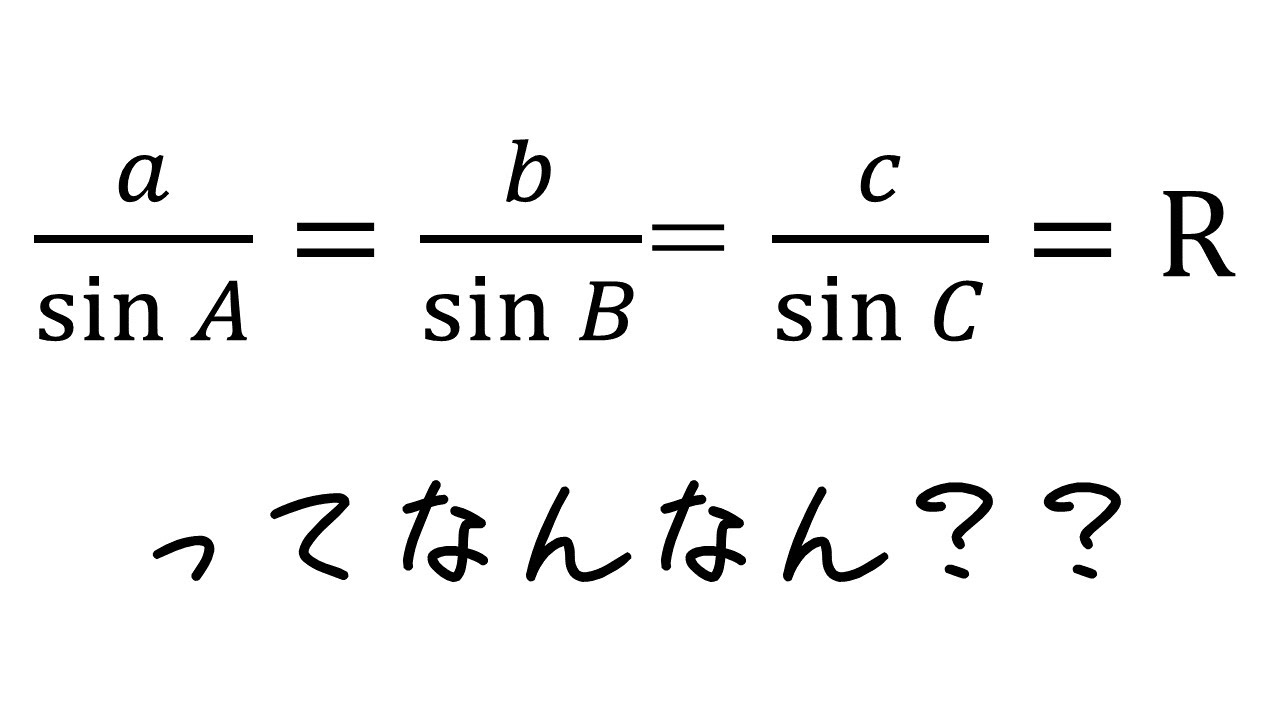
【差がつく】余弦定理の証明、できますか?【高校・数学】

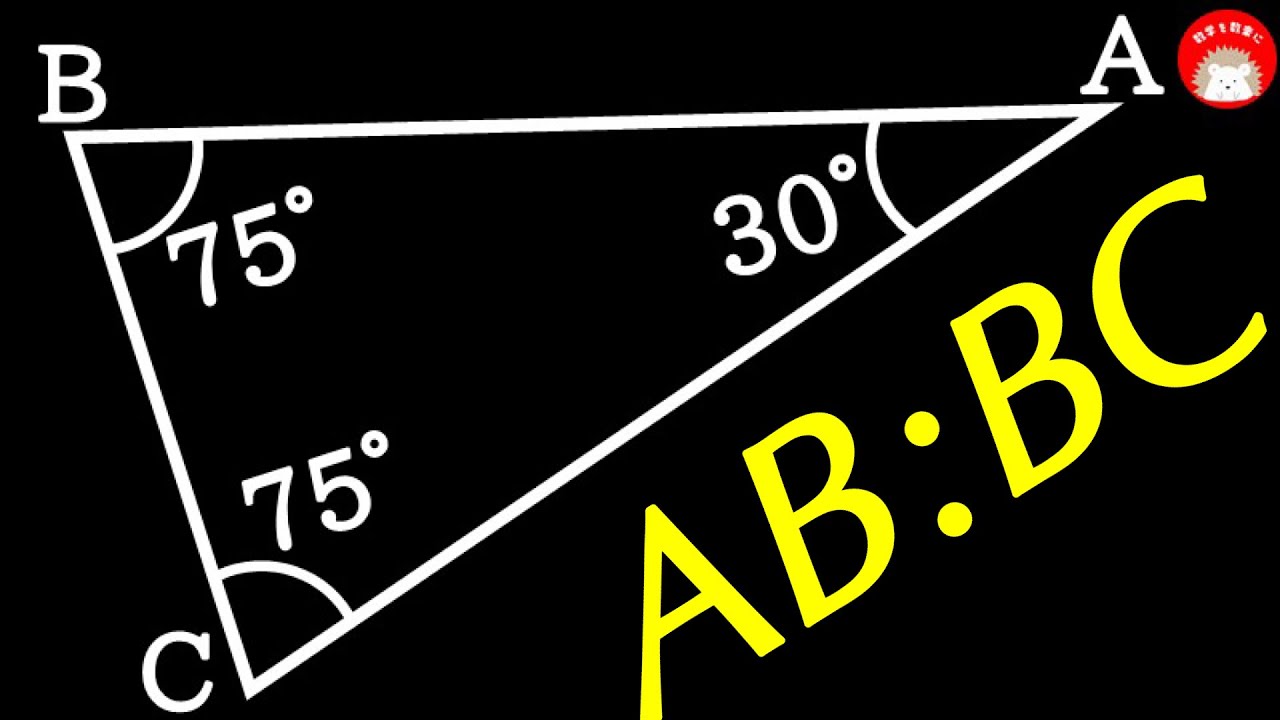
高校入試なので、正弦定理は制限して下さい。A 2021 愛知県

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の半径=6
BC=?
*図は動画内参照
2021愛知県
この動画を見る
円の半径=6
BC=?
*図は動画内参照
2021愛知県
【数学Ⅱ】半角の公式は覚えるな!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
(1) $\cos \displaystyle \frac{\pi}{8}$
(2) $\sin \displaystyle \frac{\pi}{8}$
(3) $\cos \displaystyle \frac{\pi}{12}$
この動画を見る
(1) $\cos \displaystyle \frac{\pi}{8}$
(2) $\sin \displaystyle \frac{\pi}{8}$
(3) $\cos \displaystyle \frac{\pi}{12}$
