 図形と計量
図形と計量
 図形と計量
図形と計量
面積比!! A
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
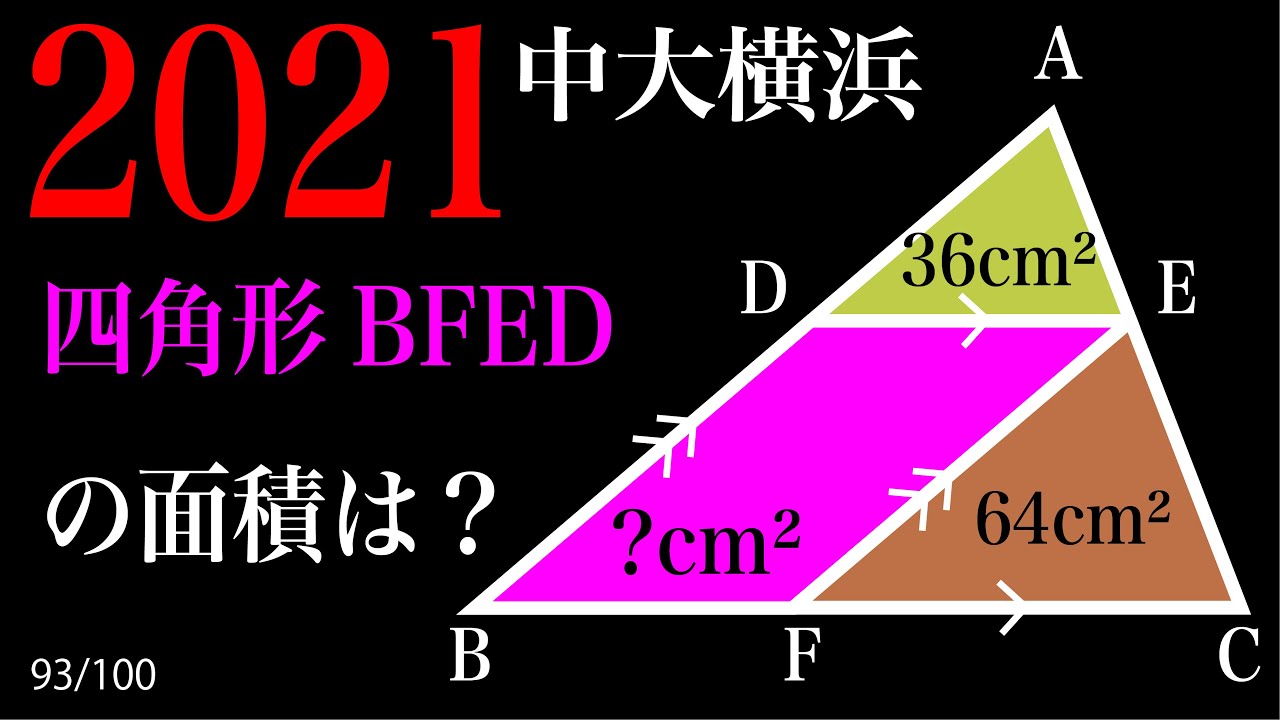
四角形BFEDの面積は?
*図は動画内参照
2021中央大学附属横浜高等学校
この動画を見る
四角形BFEDの面積は?
*図は動画内参照
2021中央大学附属横浜高等学校
関数と図形 東工大附属(改) B
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
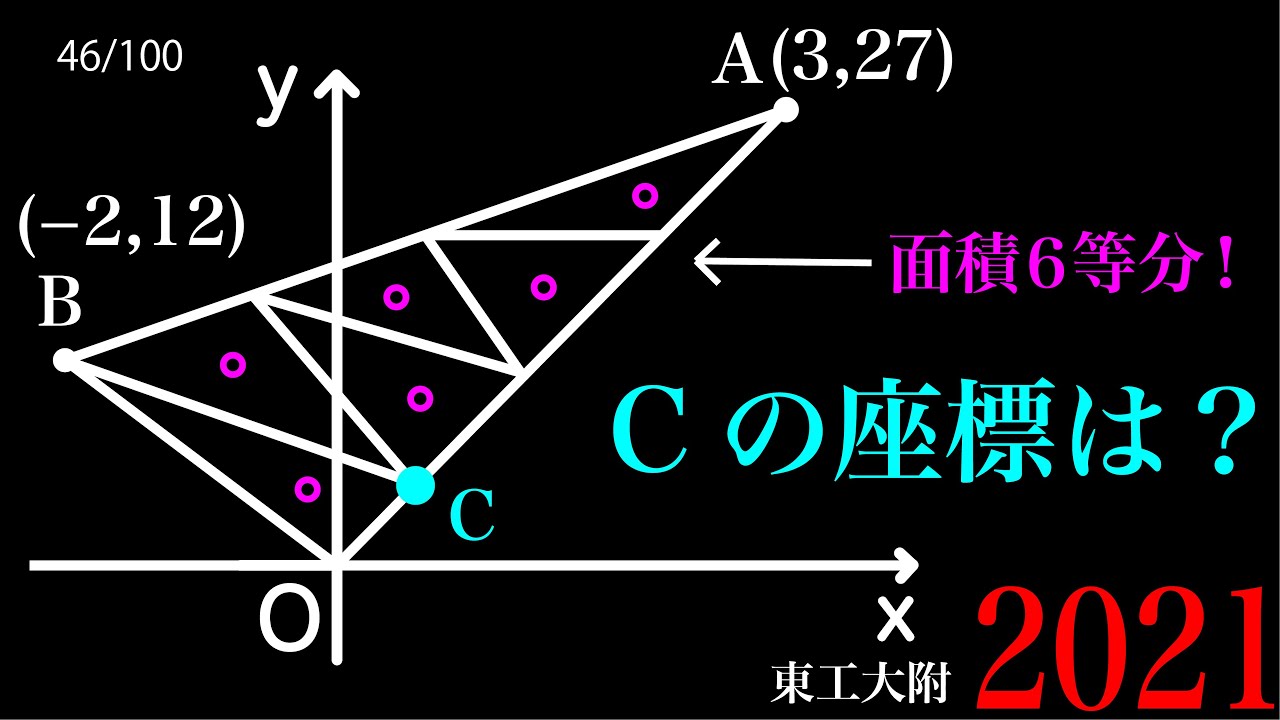
面積6等分
Cの座標は?
*図は動画内参照
2021東京工業大学附属科学技術高等学校
この動画を見る
面積6等分
Cの座標は?
*図は動画内参照
2021東京工業大学附属科学技術高等学校
【超危険】三角比が簡単に覚えられすぎちゃう!?【数学・物理】
単元:
#数Ⅰ#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
三角比$\sin \cos \tan$の覚え方解説動画です
この動画を見る
三角比$\sin \cos \tan$の覚え方解説動画です
円にできる三角形の個数 B

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
A~Hから3点選んで結び三角形を作る
(1)二等辺三角形は何コ?
(2)直角三角形は何コ?
*図は動画内参照
2021東京農業大学第一高等学校
この動画を見る
A~Hから3点選んで結び三角形を作る
(1)二等辺三角形は何コ?
(2)直角三角形は何コ?
*図は動画内参照
2021東京農業大学第一高等学校
2021 愛知高校 図形 B

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積は?
*図は動画内参照
2021愛知高等学校
この動画を見る
斜線部の面積は?
*図は動画内参照
2021愛知高等学校
共通テスト第2日程2021年数学詳しい解説〜共通テスト第2日程2021年IA第5問〜図形の性質

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第5問}$
点$Z$を端点とする半直線$ZX$と半直線$ZY$があり、$0° \lt \angle XZY \lt 90°$とする。
また、$0° \lt \angle SZX \lt \angle XZY$かつ$0° \lt \angle SZY \lt \angle XZY$を満たす点$S$をとる。
点$S$を通り、半直線$ZX$と半直線$ZY$の両方に接する円を作図したい。
円$O$を、次の$(Step\ 1)~(Step\ 5)$の手順で作図する。
手順
$(Step\ 1) \angle XZY$の二等分線$l$上に点$C$をとり、下図(※動画参照)のように半直線$ZX$
と半直線$ZY$の両方に接する円$C$を作図する。また、円$C$と半直線$ZX$との接点を$D,$
半直線$ZY$との接点を$E$とする。
$(Step\ 2)$ 円Cと直線$ZS$との交点の一つを$G$とする。
$(Step\ 3)$ 半直線$ZX$上に点$H$を$DG//HS$を満たすようにとる。
$(Step\ 4)$ 点$H$を通り、半直線$ZX$に垂直な直線を引き、$l$との交点を$O$とする。
$(Step\ 5)$ 点$O$を中心とする半径$OH$の円$O$をかく。
(1)$(Step\ 1)~(Step\ 5)$の手順で作図した円$O$が求める円であることは、次の構想に
基づいて下のように説明できる。
構想:円$O$が点$S$を通り、半直線$ZX$と半直線$ZY$の両方に接する円であることを
示すには、$OH=\boxed{\boxed{\ \ ア\ \ }}$が成り立つことを示せばよい。
作図の手順より、$\triangle ZDG$と$\triangle ZHS$との関係、および$\triangle ZDC$と$\triangle ZHO$との
関係に着目すると
$DG:\boxed{\boxed{\ \ イ\ \ }}=\boxed{\boxed{\ \ ウ\ \ }}:\boxed{\boxed{\ \ エ\ \ }}$
$DC:\boxed{\boxed{\ \ オ\ \ }}=\boxed{\boxed{\ \ ウ\ \ }}:\boxed{\boxed{\ \ エ\ \ }}$
であるから、$DG:\boxed{\boxed{\ \ イ\ \ }}=DC:\boxed{\boxed{\ \ オ\ \ }}$となる。
ここで、3点$S,O,H$が一直線上にある場合は、$\angle CDG=\angle \boxed{\boxed{\ \ カ\ \ }}$で
あるので、$\triangle CDG$と$\triangle \boxed{\boxed{\ \ カ\ \ }}$との関係に着目すると、$CD=CG$より
$OH=\boxed{\boxed{\ \ ア\ \ }}$であることがわかる。
なお、3点$S,O,H$が一直線上にある場合は、$DG=\boxed{\ \ キ\ \ }DC$となり、
$DG:\boxed{\boxed{\ \ イ\ \ }}=DC:\boxed{\boxed{\ \ オ\ \ }}$より$OH=\boxed{\boxed{\ \ ア\ \ }}$である
ことがわかる。
$\boxed{\boxed{\ \ ア\ \ }}~\boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$DH$ ①$HO$ ②$HS$ ③$OD$ ④$OG$
⑤$OS$ ⑥$ZD$ ⑦$ZH$ ⑧$ZO$ ⑨$ZS$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$OHD$ ①$OHG$ ②$OHS$ ③$ZDS$
④$ZHG$ ⑤$ZHS$ ⑥$ZOS$ ⑦$ZCG$
(2)点$S$を通り、半直線$ZX$と半直線$ZY$の両方に接する円は二つ作図できる。
特に、点$S$が$\angle XZY$の二等分線$l$上にある場合を考える。半径が大きい方の
円の中心を$O_1$とし、半径が小さい方の円の中心を$O_2$とする。また、円$O_2$と
半直線$ZY$が接する点を$I$とする。円$O_1$と半直線$ZY$が接する点を$J$とし、円$O_1$と
半直線$ZX$が接する点を$K$とする。
作図をした結果、円$O_1$の半径は$5$, 円$O_2$の半径は3であったとする。このとき、
$IJ=\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケコ\ \ }}$である。さらに、円$O_1$と円$O_2$の接点$S$に
おける共通接線と半直線$ZY$との交点を$L$とし、
直線$LK$と円$O_1$との交点で点$K$とは異なる点を$M$とすると
$LM・LK=\boxed{\ \ サシ\ \ }$
である。
また、$ZI=\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セソ\ \ }}$であるので、直線$LK$と直線$l$との交点を$N$とすると
$\displaystyle \frac{LN}{NK}=\displaystyle \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}, SN=\displaystyle \frac{\boxed{\ \ ツ\ \ }}{\boxed{\ \ テ\ \ }}$
である。
2021共通テスト過去問
この動画を見る
${\large第5問}$
点$Z$を端点とする半直線$ZX$と半直線$ZY$があり、$0° \lt \angle XZY \lt 90°$とする。
また、$0° \lt \angle SZX \lt \angle XZY$かつ$0° \lt \angle SZY \lt \angle XZY$を満たす点$S$をとる。
点$S$を通り、半直線$ZX$と半直線$ZY$の両方に接する円を作図したい。
円$O$を、次の$(Step\ 1)~(Step\ 5)$の手順で作図する。
手順
$(Step\ 1) \angle XZY$の二等分線$l$上に点$C$をとり、下図(※動画参照)のように半直線$ZX$
と半直線$ZY$の両方に接する円$C$を作図する。また、円$C$と半直線$ZX$との接点を$D,$
半直線$ZY$との接点を$E$とする。
$(Step\ 2)$ 円Cと直線$ZS$との交点の一つを$G$とする。
$(Step\ 3)$ 半直線$ZX$上に点$H$を$DG//HS$を満たすようにとる。
$(Step\ 4)$ 点$H$を通り、半直線$ZX$に垂直な直線を引き、$l$との交点を$O$とする。
$(Step\ 5)$ 点$O$を中心とする半径$OH$の円$O$をかく。
(1)$(Step\ 1)~(Step\ 5)$の手順で作図した円$O$が求める円であることは、次の構想に
基づいて下のように説明できる。
構想:円$O$が点$S$を通り、半直線$ZX$と半直線$ZY$の両方に接する円であることを
示すには、$OH=\boxed{\boxed{\ \ ア\ \ }}$が成り立つことを示せばよい。
作図の手順より、$\triangle ZDG$と$\triangle ZHS$との関係、および$\triangle ZDC$と$\triangle ZHO$との
関係に着目すると
$DG:\boxed{\boxed{\ \ イ\ \ }}=\boxed{\boxed{\ \ ウ\ \ }}:\boxed{\boxed{\ \ エ\ \ }}$
$DC:\boxed{\boxed{\ \ オ\ \ }}=\boxed{\boxed{\ \ ウ\ \ }}:\boxed{\boxed{\ \ エ\ \ }}$
であるから、$DG:\boxed{\boxed{\ \ イ\ \ }}=DC:\boxed{\boxed{\ \ オ\ \ }}$となる。
ここで、3点$S,O,H$が一直線上にある場合は、$\angle CDG=\angle \boxed{\boxed{\ \ カ\ \ }}$で
あるので、$\triangle CDG$と$\triangle \boxed{\boxed{\ \ カ\ \ }}$との関係に着目すると、$CD=CG$より
$OH=\boxed{\boxed{\ \ ア\ \ }}$であることがわかる。
なお、3点$S,O,H$が一直線上にある場合は、$DG=\boxed{\ \ キ\ \ }DC$となり、
$DG:\boxed{\boxed{\ \ イ\ \ }}=DC:\boxed{\boxed{\ \ オ\ \ }}$より$OH=\boxed{\boxed{\ \ ア\ \ }}$である
ことがわかる。
$\boxed{\boxed{\ \ ア\ \ }}~\boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$DH$ ①$HO$ ②$HS$ ③$OD$ ④$OG$
⑤$OS$ ⑥$ZD$ ⑦$ZH$ ⑧$ZO$ ⑨$ZS$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$OHD$ ①$OHG$ ②$OHS$ ③$ZDS$
④$ZHG$ ⑤$ZHS$ ⑥$ZOS$ ⑦$ZCG$
(2)点$S$を通り、半直線$ZX$と半直線$ZY$の両方に接する円は二つ作図できる。
特に、点$S$が$\angle XZY$の二等分線$l$上にある場合を考える。半径が大きい方の
円の中心を$O_1$とし、半径が小さい方の円の中心を$O_2$とする。また、円$O_2$と
半直線$ZY$が接する点を$I$とする。円$O_1$と半直線$ZY$が接する点を$J$とし、円$O_1$と
半直線$ZX$が接する点を$K$とする。
作図をした結果、円$O_1$の半径は$5$, 円$O_2$の半径は3であったとする。このとき、
$IJ=\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケコ\ \ }}$である。さらに、円$O_1$と円$O_2$の接点$S$に
おける共通接線と半直線$ZY$との交点を$L$とし、
直線$LK$と円$O_1$との交点で点$K$とは異なる点を$M$とすると
$LM・LK=\boxed{\ \ サシ\ \ }$
である。
また、$ZI=\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セソ\ \ }}$であるので、直線$LK$と直線$l$との交点を$N$とすると
$\displaystyle \frac{LN}{NK}=\displaystyle \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}, SN=\displaystyle \frac{\boxed{\ \ ツ\ \ }}{\boxed{\ \ テ\ \ }}$
である。
2021共通テスト過去問
智弁和歌山2021 A
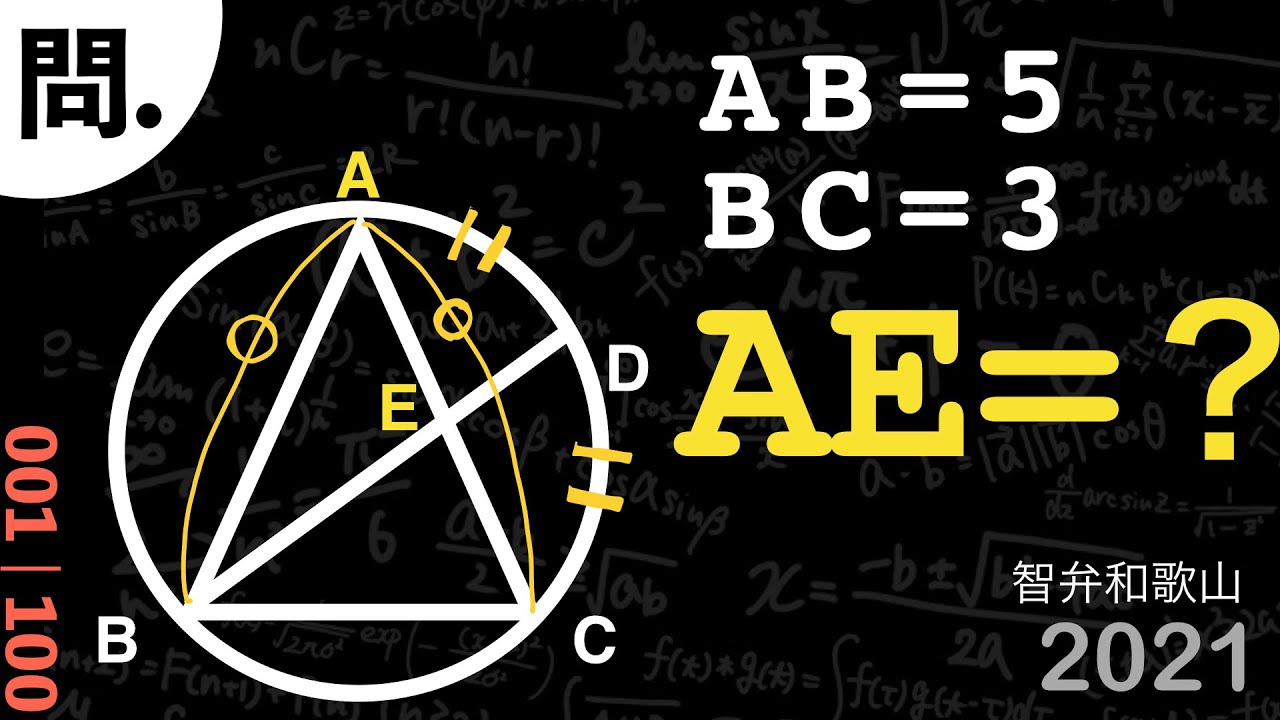
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=5,BC=3,AE=?
*図は動画内参照
2021智辯学園和歌山高等学校
この動画を見る
AB=5,BC=3,AE=?
*図は動画内参照
2021智辯学園和歌山高等学校
共通テスト第2日程2021年数学詳しい解説〜共通テスト第2日程2021年IA第1問〜2次関数と三角比

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1] $a,b$を定数とするとき、$x$についての不等式
$|ax-b-7| \lt 3$ $\cdots$①
を考える。
(1)$a=-3,b=-2$とする。①を満たす整数全体の集合を$P$とする。
この集合$P$を、要素を書き並べて表すと
$P=\left\{\boxed{\ \ アイ\ \ }, \boxed{\ \ ウエ\ \ }\right\}$
となる。ただし、$\boxed{\ \ アイ\ \ }, \boxed{\ \ ウエ\ \ }$の解答の順序は問わない。
(2)$a=\displaystyle \frac{1}{\sqrt2}$とする。
$(\textrm{i})b=1$のとき、①を満たす整数は全部で$\boxed{\ \ オ\ \ }$個である。
$(\textrm{ii})$①を満たす整数が全部で$(\boxed{\ \ オ\ \ }+1)$個であるような正の整数$b$
のうち、最小のものは$\boxed{\ \ カ\ \ }$である。
[2]平面上に2点$A,B$があり、$AB=8$である。直線$AB$上にない点$P$をとり、
$\triangle ABP$をつくり、その外接円の半径を$R$とする。
太郎さんは、図1(※動画参照)のように、コンピュータソフトを使って点$P$
をいろいろな位置に取った。
図1は、点$P$をいろいろな位置にとったときの$\triangle$の外接円をかいたものである。
(1)太郎さんは、点$P$のとり方によって外接円の半径が異なることに気づき、
次の問題1を考えることにした。
問題1:点$P$をいろいろな位置にとるとき、外接円の半径$R$が最小となる
$\triangle ABP$はどのような三角形か。
正弦定理により、$2R=\displaystyle \frac{\boxed{\ \ キ\ \ }}{\sin\angle APB}$である。よって、
Rが最小となるのは$\angle APB=\boxed{\ \ クケ\ \ }°$の三角形である。
このとき、$R=\boxed{\ \ コ\ \ }$である。
(2)太郎さんは、図2(※動画参照)のように、問題1の点$P$のとり方に
条件を付けて、次の問題2を考えた。
問題2:直線$AB$に平行な直線を$l$とし、直線l上で点$P$をいろいろな
位置にとる。このとき、外接円の半径$R$が最小となる$\triangle ABP$は
どのような三角形か。
太郎さんは、この問題を解決するために、次の構想を立てた。
問題2の解決の構想
問題1の考察から、線分$AB$を直径とする円を$C$とし、円$C$に着目
する。直線lは、その位置によって、円$C$と共有点を持つ場合と
もたない場合があるので、それぞれの場合に分けて考える。
直線$AB$と直線lとの距離を$h$とする。直線lが円$C$と共有点を
持つ場合は、$h \leqq \boxed{\ \ サ\ \ }$のときであり、共有点をもたない場合は、
$h \gt \boxed{\ \ サ\ \ }$のときである。
$(\textrm{i})h \leqq \boxed{\ \ サ\ \ }$のとき
直線$l$が円$C$と共有点をもつので、$R$が最小となる$\triangle ABP$は、
$h \lt \boxed{\ \ サ\ \ }$のとき$\boxed{\boxed{\ \ シ\ \ }}$であり、$h=\boxed{\ \ サ\ \ }$のとき直角二等辺三角形
である。
$(\textrm{ii})h \gt \boxed{\ \ サ\ \ }$のとき
線分$AB$の垂直二等分線を$m$とし、直線$m$と直線$l$との交点を$P_1$とする。
直線$l$上にあり点$P_1$とは異なる点を$P_2$とするとき$\sin\angle AP_1B$
と$\sin\angle AP_2B$の大小を考える。
$\triangle ABP_2$の外接円と直線$m$との共有点のうち、直線$AB$に関して点$P_2$
と同じ側にある点を$P_3$とすると、$\angle AP_3B \boxed{\boxed{\ \ ス\ \ }}\angle AP_2B$である。
また、$\angle AP_3B \lt \angle AP_1B \lt 90°$より$\sin \angle AP_3B \boxed{\boxed{\ \ セ\ \ }}\angle AP_1B$である。
このとき$(\triangle ABP_1$の外接円の半径$) \boxed{\boxed{\ \ ソ\ \ }} (\triangle ABP_2$の外接円の半径)
であり、$R$が最小となる$\triangle ABP$は$\boxed{\boxed{\ \ タ\ \ }}$である。
$\boxed{\boxed{\ \ シ\ \ }}, \boxed{\boxed{\ \ タ\ \ }}$については、最も適当なものを、次の⓪~④のうち
から一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
⓪鈍角三角形 ①直角三角形 ②正三角形
③二等辺三角形 ④直角二等辺三角形
$\boxed{\boxed{\ \ ス\ \ }}~\boxed{\boxed{\ \ ソ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\lt$ ①$=$ ②$\gt$
(3)問題2の考察を振り返って、$h=8$のとき、$\triangle ABP$の外接円の半径$R$
が最小である場合について考える。このとき、$\sin\angle APB=\displaystyle \frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$
であり、$R=\boxed{\ \ テ\ \ }$である。
2021共通テスト過去問
この動画を見る
${\large第1問}$
[1] $a,b$を定数とするとき、$x$についての不等式
$|ax-b-7| \lt 3$ $\cdots$①
を考える。
(1)$a=-3,b=-2$とする。①を満たす整数全体の集合を$P$とする。
この集合$P$を、要素を書き並べて表すと
$P=\left\{\boxed{\ \ アイ\ \ }, \boxed{\ \ ウエ\ \ }\right\}$
となる。ただし、$\boxed{\ \ アイ\ \ }, \boxed{\ \ ウエ\ \ }$の解答の順序は問わない。
(2)$a=\displaystyle \frac{1}{\sqrt2}$とする。
$(\textrm{i})b=1$のとき、①を満たす整数は全部で$\boxed{\ \ オ\ \ }$個である。
$(\textrm{ii})$①を満たす整数が全部で$(\boxed{\ \ オ\ \ }+1)$個であるような正の整数$b$
のうち、最小のものは$\boxed{\ \ カ\ \ }$である。
[2]平面上に2点$A,B$があり、$AB=8$である。直線$AB$上にない点$P$をとり、
$\triangle ABP$をつくり、その外接円の半径を$R$とする。
太郎さんは、図1(※動画参照)のように、コンピュータソフトを使って点$P$
をいろいろな位置に取った。
図1は、点$P$をいろいろな位置にとったときの$\triangle$の外接円をかいたものである。
(1)太郎さんは、点$P$のとり方によって外接円の半径が異なることに気づき、
次の問題1を考えることにした。
問題1:点$P$をいろいろな位置にとるとき、外接円の半径$R$が最小となる
$\triangle ABP$はどのような三角形か。
正弦定理により、$2R=\displaystyle \frac{\boxed{\ \ キ\ \ }}{\sin\angle APB}$である。よって、
Rが最小となるのは$\angle APB=\boxed{\ \ クケ\ \ }°$の三角形である。
このとき、$R=\boxed{\ \ コ\ \ }$である。
(2)太郎さんは、図2(※動画参照)のように、問題1の点$P$のとり方に
条件を付けて、次の問題2を考えた。
問題2:直線$AB$に平行な直線を$l$とし、直線l上で点$P$をいろいろな
位置にとる。このとき、外接円の半径$R$が最小となる$\triangle ABP$は
どのような三角形か。
太郎さんは、この問題を解決するために、次の構想を立てた。
問題2の解決の構想
問題1の考察から、線分$AB$を直径とする円を$C$とし、円$C$に着目
する。直線lは、その位置によって、円$C$と共有点を持つ場合と
もたない場合があるので、それぞれの場合に分けて考える。
直線$AB$と直線lとの距離を$h$とする。直線lが円$C$と共有点を
持つ場合は、$h \leqq \boxed{\ \ サ\ \ }$のときであり、共有点をもたない場合は、
$h \gt \boxed{\ \ サ\ \ }$のときである。
$(\textrm{i})h \leqq \boxed{\ \ サ\ \ }$のとき
直線$l$が円$C$と共有点をもつので、$R$が最小となる$\triangle ABP$は、
$h \lt \boxed{\ \ サ\ \ }$のとき$\boxed{\boxed{\ \ シ\ \ }}$であり、$h=\boxed{\ \ サ\ \ }$のとき直角二等辺三角形
である。
$(\textrm{ii})h \gt \boxed{\ \ サ\ \ }$のとき
線分$AB$の垂直二等分線を$m$とし、直線$m$と直線$l$との交点を$P_1$とする。
直線$l$上にあり点$P_1$とは異なる点を$P_2$とするとき$\sin\angle AP_1B$
と$\sin\angle AP_2B$の大小を考える。
$\triangle ABP_2$の外接円と直線$m$との共有点のうち、直線$AB$に関して点$P_2$
と同じ側にある点を$P_3$とすると、$\angle AP_3B \boxed{\boxed{\ \ ス\ \ }}\angle AP_2B$である。
また、$\angle AP_3B \lt \angle AP_1B \lt 90°$より$\sin \angle AP_3B \boxed{\boxed{\ \ セ\ \ }}\angle AP_1B$である。
このとき$(\triangle ABP_1$の外接円の半径$) \boxed{\boxed{\ \ ソ\ \ }} (\triangle ABP_2$の外接円の半径)
であり、$R$が最小となる$\triangle ABP$は$\boxed{\boxed{\ \ タ\ \ }}$である。
$\boxed{\boxed{\ \ シ\ \ }}, \boxed{\boxed{\ \ タ\ \ }}$については、最も適当なものを、次の⓪~④のうち
から一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
⓪鈍角三角形 ①直角三角形 ②正三角形
③二等辺三角形 ④直角二等辺三角形
$\boxed{\boxed{\ \ ス\ \ }}~\boxed{\boxed{\ \ ソ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\lt$ ①$=$ ②$\gt$
(3)問題2の考察を振り返って、$h=8$のとき、$\triangle ABP$の外接円の半径$R$
が最小である場合について考える。このとき、$\sin\angle APB=\displaystyle \frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$
であり、$R=\boxed{\ \ テ\ \ }$である。
2021共通テスト過去問
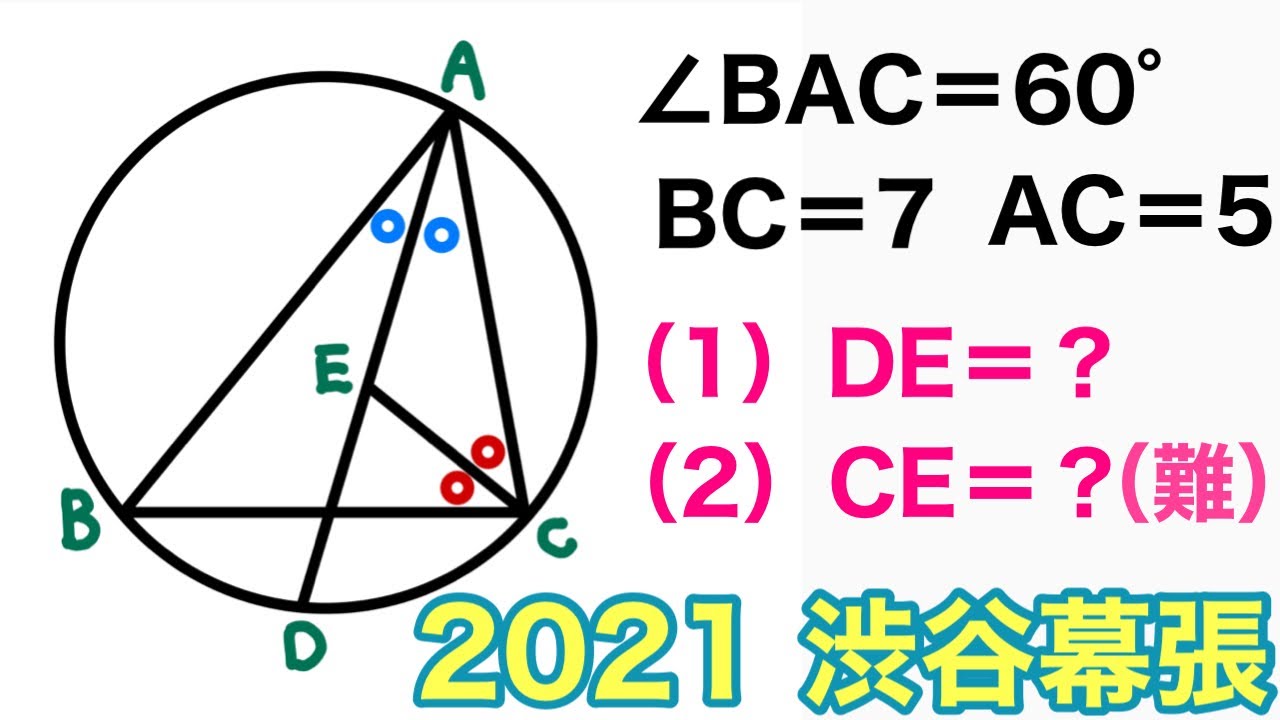
2021渋谷幕張 円 D
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle BAC=60°$
(1)DE=?
(2)CE=?
*図は動画内参照
2021渋谷教育学園幕張高等学校
この動画を見る
$\angle BAC=60°$
(1)DE=?
(2)CE=?
*図は動画内参照
2021渋谷教育学園幕張高等学校
共通テスト2021年数学詳しい解説〜共通テスト2021年IA第1問〜2次関数、三角比

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1]$c$を正の整数とする。$x$の2次方程式
$2x^2+(4c-3)x+2c^2$$-c-11=0$ $\cdots$①
について考える。
(1)$c=1$のとき、①のっ左辺を因数分解すると
$\left(\boxed{\ \ ア\ \ }\ x+\boxed{\ \ イ\ \ }\right)\left(x-\boxed{\ \ ウ\ \ }\right)$
であるから、①の解は
$x=-\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ア\ \ }},\ \boxed{\ \ ウ\ \ }$
である。
(2)$c=2$のとき、①の解は
$x=\displaystyle \frac{-\boxed{\ \ エ\ \ }\pm\sqrt{\boxed{\ \ オカ\ \ }}}{\boxed{\ \ キ\ \ }}$
であり、大きい方の解を$\alpha$とすると
$\displaystyle \frac{5}{\alpha}=\displaystyle \frac{\boxed{\ \ ク\ \ }\pm\sqrt{\boxed{\ \ ケコ\ \ }}}{\boxed{\ \ サ\ \ }}$
である。また、$m \lt \displaystyle \frac{5}{\alpha} \lt m+1$を満たす整数$m$は$\boxed{\ \ シ\ \ }$である。
(3)太郎さんと花子さんは、①の解について考察している。
太郎:①の解は$c$の値によって、ともに有理数である場合も
あれば、ともに無理数である場合もあるね。$c$がどの
ような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すれば
いいんじゃないかな。
①の解が異なる二つの有理数であるような正の整数$c$の個数は
$\boxed{\ \ ス\ \ }$個である。
[2]右の図のように(※動画参照)、$\triangle ABC$の外側に辺$AB,BC,CA$
をそれぞれ1辺とする正方形$ADEB,BFGC,CHIA$をかき、
2点$E$と$F,G$と$H,I$と$D$をそれぞれ線分で結んだ図形を考える。
以下において
$BC=a, CA=b, AB=c$
$\angle CAB=A, \angle ABC=B, $$\angle BCA=C$
とする。
(1)$b=6,c=5,\cos A=\displaystyle \frac{3}{5}$のとき、$\sin A=\displaystyle \frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}$であり、
$\triangle ABC$の面積は$\boxed{\ \ タチ\ \ }、\triangle AID$の面積は$\boxed{\ \ ツテ\ \ }$である。
(2)正方形$BFGC, CHIA, ADEB$の面積をそれぞれ$S_1,S_2,S_3$とする。
このとき、$S_1-S_2-S_3$は
・$0° \lt A \lt 90°$のとき、$\boxed{\boxed{\ \ ト\ \ }}$。
・$A=90°$のとき、$\boxed{\boxed{\ \ ナ\ \ }}$。
・$90° \lt A \lt 180°$のとき、$\boxed{\boxed{\ \ ニ\ \ }}$。
$\boxed{\boxed{\ \ ト\ \ }}~\boxed{\boxed{\ \ ニ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$0$である
①正の値である
②負の値である
③正の値も負の値もとる
(3)$\triangle AID,\triangle BEF,\triangle CGH$の面積をそれぞれ$T_1,T_2,T_3$とする。
このとき、$\boxed{\boxed{\ \ ヌ\ \ }}$である。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪$a \lt b \lt c$ならば、$T_1 \gt T_2 \gt T_3$
①$a \lt b \lt c$ならば、$T_1 \lt T_2 \lt T_3$
②$A$が鈍角ならば、$T_1 \lt T_2かつT_2 \lt T_3$
③$a,b,c$の値に関係なく、$T_1=T_2=T_3$
(4)$\triangle ABC,\triangle AID,\triangle BEF,\triangle CGH$のうち、外接円の半径が最も小さい
ものを求める。
$0° \lt A \lt 90°$のとき、$ID \boxed{\boxed{\ \ ネ\ \ }}BC$であり
($\triangle AID$の外接円の半径)$\boxed{\boxed{\ \ ノ\ \ }}$($\triangle ABC$の外接円の半径)
であるから、外接円の半径が最も小さい三角形は
・$0° \lt A \lt B \lt C \lt 90°$のとき、$\boxed{\boxed{\ \ ハ\ \ }}$である。
・$0° \lt A \lt B \lt 90° \lt $Cのとき、$\boxed{\boxed{\ \ ヒ\ \ }}$である。
$\boxed{\boxed{\ \ ネ\ \ }},\boxed{\boxed{\ \ ノ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\lt$ ①$=$ ②$\gt$
$\boxed{\boxed{\ \ ハ\ \ }},\boxed{\boxed{\ \ ヒ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\triangle ABC$ ①$\triangle AID$ ②$\triangle BEF$ ③$\triangle CGH$
2021共通テスト過去問
この動画を見る
${\large第1問}$
[1]$c$を正の整数とする。$x$の2次方程式
$2x^2+(4c-3)x+2c^2$$-c-11=0$ $\cdots$①
について考える。
(1)$c=1$のとき、①のっ左辺を因数分解すると
$\left(\boxed{\ \ ア\ \ }\ x+\boxed{\ \ イ\ \ }\right)\left(x-\boxed{\ \ ウ\ \ }\right)$
であるから、①の解は
$x=-\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ア\ \ }},\ \boxed{\ \ ウ\ \ }$
である。
(2)$c=2$のとき、①の解は
$x=\displaystyle \frac{-\boxed{\ \ エ\ \ }\pm\sqrt{\boxed{\ \ オカ\ \ }}}{\boxed{\ \ キ\ \ }}$
であり、大きい方の解を$\alpha$とすると
$\displaystyle \frac{5}{\alpha}=\displaystyle \frac{\boxed{\ \ ク\ \ }\pm\sqrt{\boxed{\ \ ケコ\ \ }}}{\boxed{\ \ サ\ \ }}$
である。また、$m \lt \displaystyle \frac{5}{\alpha} \lt m+1$を満たす整数$m$は$\boxed{\ \ シ\ \ }$である。
(3)太郎さんと花子さんは、①の解について考察している。
太郎:①の解は$c$の値によって、ともに有理数である場合も
あれば、ともに無理数である場合もあるね。$c$がどの
ような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すれば
いいんじゃないかな。
①の解が異なる二つの有理数であるような正の整数$c$の個数は
$\boxed{\ \ ス\ \ }$個である。
[2]右の図のように(※動画参照)、$\triangle ABC$の外側に辺$AB,BC,CA$
をそれぞれ1辺とする正方形$ADEB,BFGC,CHIA$をかき、
2点$E$と$F,G$と$H,I$と$D$をそれぞれ線分で結んだ図形を考える。
以下において
$BC=a, CA=b, AB=c$
$\angle CAB=A, \angle ABC=B, $$\angle BCA=C$
とする。
(1)$b=6,c=5,\cos A=\displaystyle \frac{3}{5}$のとき、$\sin A=\displaystyle \frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}$であり、
$\triangle ABC$の面積は$\boxed{\ \ タチ\ \ }、\triangle AID$の面積は$\boxed{\ \ ツテ\ \ }$である。
(2)正方形$BFGC, CHIA, ADEB$の面積をそれぞれ$S_1,S_2,S_3$とする。
このとき、$S_1-S_2-S_3$は
・$0° \lt A \lt 90°$のとき、$\boxed{\boxed{\ \ ト\ \ }}$。
・$A=90°$のとき、$\boxed{\boxed{\ \ ナ\ \ }}$。
・$90° \lt A \lt 180°$のとき、$\boxed{\boxed{\ \ ニ\ \ }}$。
$\boxed{\boxed{\ \ ト\ \ }}~\boxed{\boxed{\ \ ニ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$0$である
①正の値である
②負の値である
③正の値も負の値もとる
(3)$\triangle AID,\triangle BEF,\triangle CGH$の面積をそれぞれ$T_1,T_2,T_3$とする。
このとき、$\boxed{\boxed{\ \ ヌ\ \ }}$である。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪$a \lt b \lt c$ならば、$T_1 \gt T_2 \gt T_3$
①$a \lt b \lt c$ならば、$T_1 \lt T_2 \lt T_3$
②$A$が鈍角ならば、$T_1 \lt T_2かつT_2 \lt T_3$
③$a,b,c$の値に関係なく、$T_1=T_2=T_3$
(4)$\triangle ABC,\triangle AID,\triangle BEF,\triangle CGH$のうち、外接円の半径が最も小さい
ものを求める。
$0° \lt A \lt 90°$のとき、$ID \boxed{\boxed{\ \ ネ\ \ }}BC$であり
($\triangle AID$の外接円の半径)$\boxed{\boxed{\ \ ノ\ \ }}$($\triangle ABC$の外接円の半径)
であるから、外接円の半径が最も小さい三角形は
・$0° \lt A \lt B \lt C \lt 90°$のとき、$\boxed{\boxed{\ \ ハ\ \ }}$である。
・$0° \lt A \lt B \lt 90° \lt $Cのとき、$\boxed{\boxed{\ \ ヒ\ \ }}$である。
$\boxed{\boxed{\ \ ネ\ \ }},\boxed{\boxed{\ \ ノ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\lt$ ①$=$ ②$\gt$
$\boxed{\boxed{\ \ ハ\ \ }},\boxed{\boxed{\ \ ヒ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\triangle ABC$ ①$\triangle AID$ ②$\triangle BEF$ ③$\triangle CGH$
2021共通テスト過去問
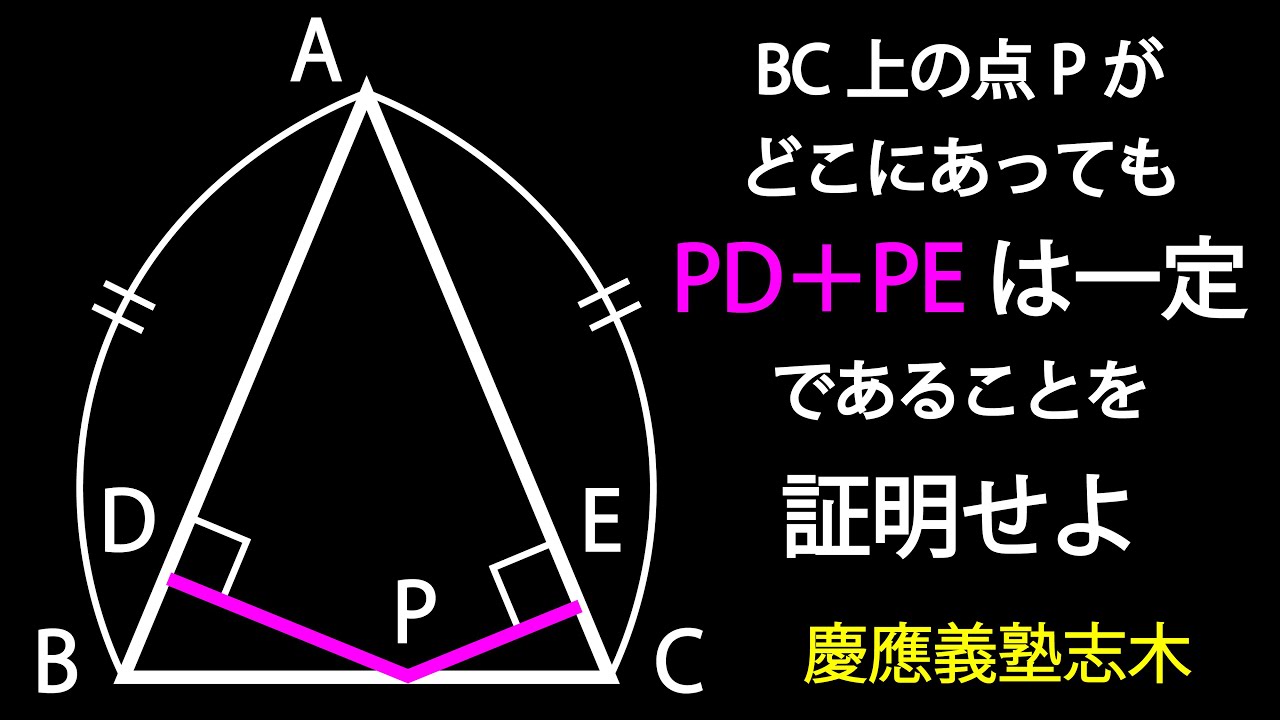
一定であることの証明 慶應志木
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
PD+PE=一定であることを証明せよ。
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
PD+PE=一定であることを証明せよ。
*図は動画内参照
慶應義塾志木高等学校
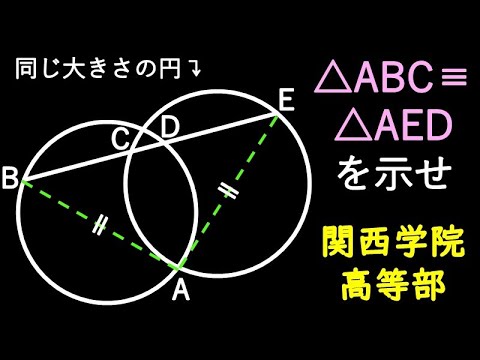
円 三角形の合同の証明 B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
同じ大きさの円
△ABC≡△AEDを示せ
*図は動画内参照
関西学院高等部
この動画を見る
同じ大きさの円
△ABC≡△AEDを示せ
*図は動画内参照
関西学院高等部
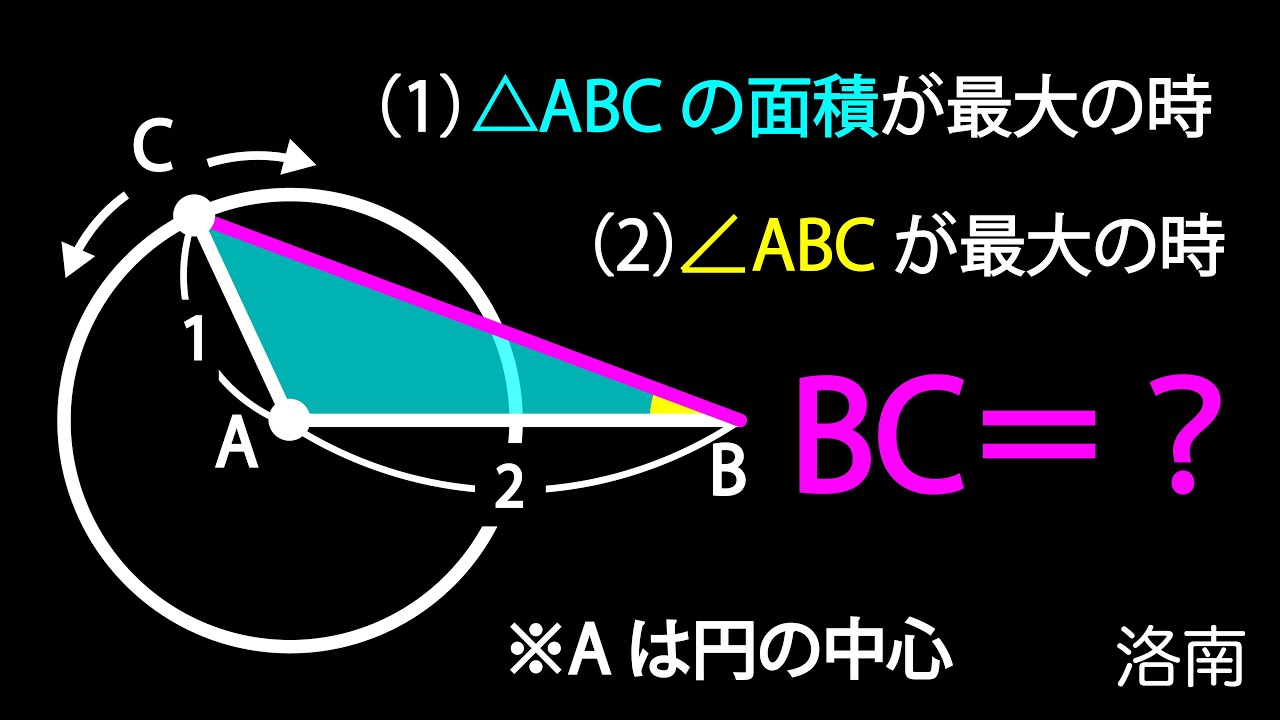
円 面積最大 角度最大 A
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)△ABCの面積が最大の時
(2)$\angle ABC$が最大の時
BC=?
*図は動画内参照
洛南高等学校
この動画を見る
(1)△ABCの面積が最大の時
(2)$\angle ABC$が最大の時
BC=?
*図は動画内参照
洛南高等学校
「正弦定理・余弦定理・面積公式」【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
正弦定理・余弦定理・面積公式の解説動画です
この動画を見る
正弦定理・余弦定理・面積公式の解説動画です
「三角比の最大値と最小値」【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
三角比の最大値と最小値の解説動画です
この動画を見る
三角比の最大値と最小値の解説動画です
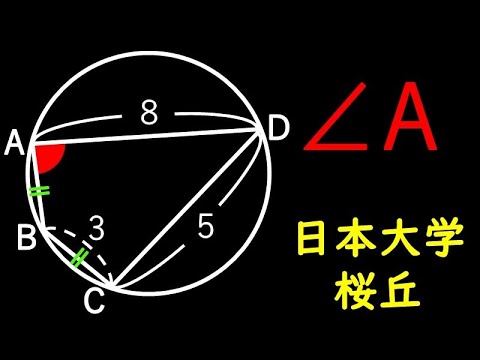
角度を求める C 日大桜ヶ丘
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle A=?$
*図は動画内参照
日本大学櫻丘高等学校
この動画を見る
$\angle A=?$
*図は動画内参照
日本大学櫻丘高等学校
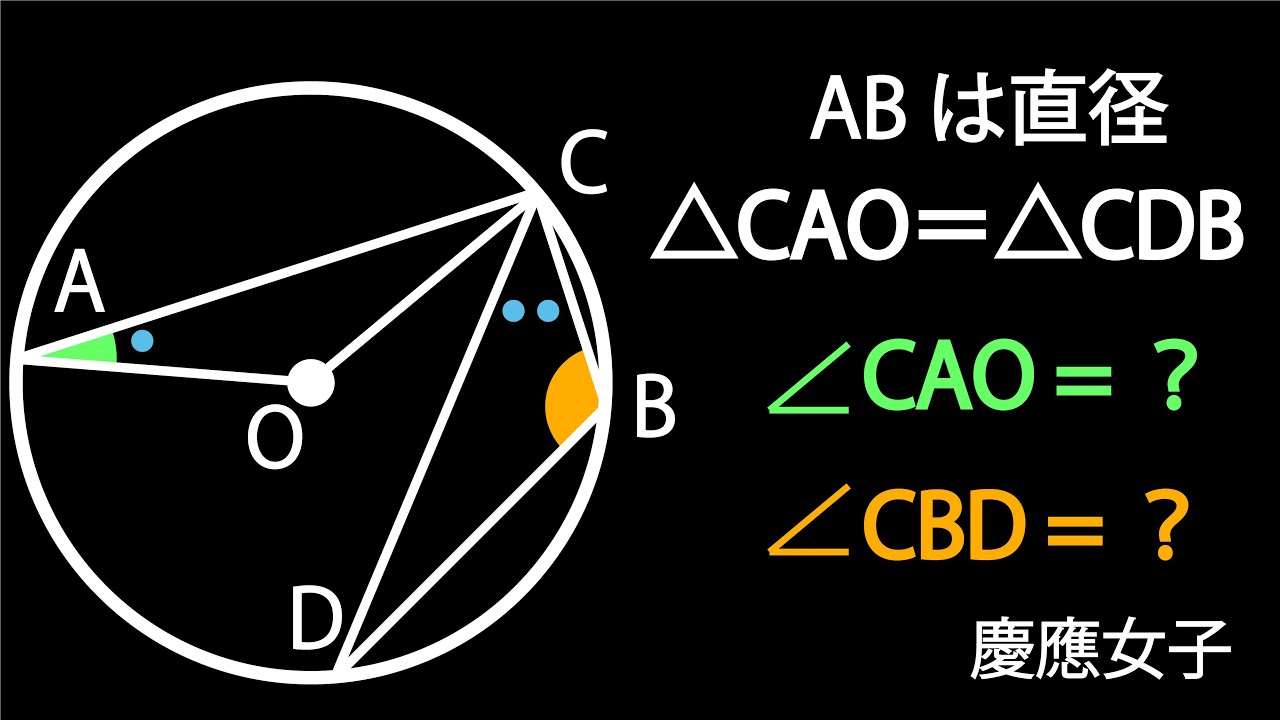
円と角度 慶應女子B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△CAO=△CDB
$\angle CAO = ?$
$\angle CBD = ?$
*図は動画内参照
慶應義塾女子高等学校
この動画を見る
△CAO=△CDB
$\angle CAO = ?$
$\angle CBD = ?$
*図は動画内参照
慶應義塾女子高等学校
「三角比(方程式と不等式)」【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の三角方程式、不等式を解け。
ただし、$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$とする。
(1)
$\cos\theta=\displaystyle \frac{1}{2}$
$\theta=60^{ \circ }$
(2)
$\sin\theta=\displaystyle \frac{1}{\sqrt{ 2 }}$
$\theta=45^{ \circ },135^{ \circ }$
(3)
$\tan\theta=\displaystyle \frac{1}{\sqrt{ 3 }}$
$\theta=150^{ \circ }$
(4)
$2\cos\theta+\sqrt{ 3 }=0$
$\cos\theta=-\displaystyle \frac{\sqrt{ 3 }}{2}$より
$\theta=150^{ \circ }$
(5)
$\sqrt{ 3 }\tan\theta-3=0$
$\tan\theta=\sqrt{ 3 }$より
$\theta=60^{ \circ }$
(6)
$2\sin^2\theta-5\cos\theta+1=0$
$2(1-\cos^2\theta)-5\cos\theta+1=0$
$2\cos^2\theta+5\cos\theta-3=0$
$-1 \leqq \cos\theta \leqq 1$より$\cos\theta+3=0$
したがって$2\cos\theta-1=0$
$\cos\theta=\displaystyle \frac{1}{2}$より$\theta=60^{ \circ }$
この動画を見る
次の三角方程式、不等式を解け。
ただし、$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$とする。
(1)
$\cos\theta=\displaystyle \frac{1}{2}$
$\theta=60^{ \circ }$
(2)
$\sin\theta=\displaystyle \frac{1}{\sqrt{ 2 }}$
$\theta=45^{ \circ },135^{ \circ }$
(3)
$\tan\theta=\displaystyle \frac{1}{\sqrt{ 3 }}$
$\theta=150^{ \circ }$
(4)
$2\cos\theta+\sqrt{ 3 }=0$
$\cos\theta=-\displaystyle \frac{\sqrt{ 3 }}{2}$より
$\theta=150^{ \circ }$
(5)
$\sqrt{ 3 }\tan\theta-3=0$
$\tan\theta=\sqrt{ 3 }$より
$\theta=60^{ \circ }$
(6)
$2\sin^2\theta-5\cos\theta+1=0$
$2(1-\cos^2\theta)-5\cos\theta+1=0$
$2\cos^2\theta+5\cos\theta-3=0$
$-1 \leqq \cos\theta \leqq 1$より$\cos\theta+3=0$
したがって$2\cos\theta-1=0$
$\cos\theta=\displaystyle \frac{1}{2}$より$\theta=60^{ \circ }$
補助線のセンス問われます 円と三平方の定理 中央大附属

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径=2
BH=?
*図は動画内参照
中央大学附属高等学校
この動画を見る
半径=2
BH=?
*図は動画内参照
中央大学附属高等学校
「三角比sin(90°–θ)など」【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の値を求めよ。
$\sin7^{ \circ }-\cos83^{ \circ }-\sin97^{ \circ }-\cos173^{ \circ }$
この動画を見る
次の値を求めよ。
$\sin7^{ \circ }-\cos83^{ \circ }-\sin97^{ \circ }-\cos173^{ \circ }$
「三角比の値と相互関係」【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
1.$\sin\theta,\cos\theta,\tan\theta$のうち、1つが次のように与えられたとき、他の2つの値を求めよ。
(1)$\sin\theta=\displaystyle \frac{1}{3}(0^{ \circ } \leqq \theta \leqq 180^{ \circ })$
$\sin^2\theta+\cos^2\theta=1$より
$\left[ \dfrac{ 1 }{ 3 } \right]+\cos^2\theta=1$
$\cos^2\theta=\displaystyle \frac{8}{9}$ $\Rightarrow\cos\theta=\pm \displaystyle \frac{2\sqrt{ 2 }}{3}$
$\tan\theta=\displaystyle \frac{\sin\theta}{\cos\theta}$より
$\tan\theta=\displaystyle \frac{1}{3}\div\left[ \pm \dfrac{ 2\sqrt{ 2 } }{ 3 } \right]$
$=\pm \displaystyle \frac{1}{2\sqrt{ 2 }}=\pm \displaystyle \frac{\sqrt{ 2 }}{4}$
(2)$\tan\theta=-3(0^{ \circ } \leqq \theta \leqq 180^{ \circ })$
$1+\tan^2\theta=\displaystyle \frac{1}{\cos^2\theta}$より
$2+(-3)^2=\displaystyle \frac{1}{\cos^2\theta}$
$\cos^2\theta=\displaystyle \frac{1}{10}$
ここで、$\tan\theta \lt 0$より$\cos\theta \lt 0$であるから
$\cos\theta=-\displaystyle \frac{1}{\sqrt{ 10 }}$
$\tan\theta=\displaystyle \frac{\sin\theta}{ \cos\theta }$より$\sin\theta=\tan\theta\cos\theta$
$\tan\theta=-3\left[ -\dfrac{ 1 }{ \sqrt{ 10 } } \right]=\displaystyle \frac{3}{ \sqrt{ 10 } }$
この動画を見る
1.$\sin\theta,\cos\theta,\tan\theta$のうち、1つが次のように与えられたとき、他の2つの値を求めよ。
(1)$\sin\theta=\displaystyle \frac{1}{3}(0^{ \circ } \leqq \theta \leqq 180^{ \circ })$
$\sin^2\theta+\cos^2\theta=1$より
$\left[ \dfrac{ 1 }{ 3 } \right]+\cos^2\theta=1$
$\cos^2\theta=\displaystyle \frac{8}{9}$ $\Rightarrow\cos\theta=\pm \displaystyle \frac{2\sqrt{ 2 }}{3}$
$\tan\theta=\displaystyle \frac{\sin\theta}{\cos\theta}$より
$\tan\theta=\displaystyle \frac{1}{3}\div\left[ \pm \dfrac{ 2\sqrt{ 2 } }{ 3 } \right]$
$=\pm \displaystyle \frac{1}{2\sqrt{ 2 }}=\pm \displaystyle \frac{\sqrt{ 2 }}{4}$
(2)$\tan\theta=-3(0^{ \circ } \leqq \theta \leqq 180^{ \circ })$
$1+\tan^2\theta=\displaystyle \frac{1}{\cos^2\theta}$より
$2+(-3)^2=\displaystyle \frac{1}{\cos^2\theta}$
$\cos^2\theta=\displaystyle \frac{1}{10}$
ここで、$\tan\theta \lt 0$より$\cos\theta \lt 0$であるから
$\cos\theta=-\displaystyle \frac{1}{\sqrt{ 10 }}$
$\tan\theta=\displaystyle \frac{\sin\theta}{ \cos\theta }$より$\sin\theta=\tan\theta\cos\theta$
$\tan\theta=-3\left[ -\dfrac{ 1 }{ \sqrt{ 10 } } \right]=\displaystyle \frac{3}{ \sqrt{ 10 } }$
「三角比(図形と計量)」【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
三角比(図形と計量)の解説動画です
この動画を見る
三角比(図形と計量)の解説動画です
数検準1級1次過去問【2020年12月】3番:三角形の面積(ベクトル)

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比への応用(正弦・余弦・面積)#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$ $0(0,0,0),A(-2,1,1)B(-1,2,0)$を頂点に持つ
$\triangle{OAB}$の面積$S$を求めよ.
この動画を見る
$\boxed{3}$ $0(0,0,0),A(-2,1,1)B(-1,2,0)$を頂点に持つ
$\triangle{OAB}$の面積$S$を求めよ.
東大 三角比と漸化式

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
この動画を見る
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
cos15°を余弦定理と正弦定理で求める方法

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
cos15°を余弦定理と正弦定理で求める方法解説動画です
この動画を見る
cos15°を余弦定理と正弦定理で求める方法解説動画です
14兵庫県教員採用試験(数学:1-5番 解と係数の関係)

単元:
#数Ⅰ#数Ⅱ#複素数と方程式#図形と計量#三角比(三角比・拡張・相互関係・単位円)#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(5)
$8x^2+kx-3=0,x=sinθ,cosθ$のときkの値を求めよ。
この動画を見る
1⃣-(5)
$8x^2+kx-3=0,x=sinθ,cosθ$のときkの値を求めよ。
【数Ⅰ】図形と計量: 0°≦x≦180°のとき、関数y=sin²x+cosx+1の最大値、最小値を求めましょう。

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
教材:
#高校リード問題集#高校リード問題集数Ⅰ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0°≦x≦180°$のとき、関数$y=sin²x+cosx+1$の最大値、最小値を求めよ。
この動画を見る
$0°≦x≦180°$のとき、関数$y=sin²x+cosx+1$の最大値、最小値を求めよ。
京都府採用試験数学【2016】

単元:
#数Ⅰ#数A#数Ⅱ#数と式#場合の数と確率#平面上のベクトル#複素数平面#図形と計量#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#整数の性質#場合の数#確率#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#微分とその応用#積分とその応用#複素数平面#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#数学(高校生)#数C#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
*図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
この動画を見る
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
*図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
【数学】正弦定理の証明は覚えなくても、当たり前のように発想できます【発想の仕方の解説】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学】正弦定理の証明についての説明動画です
-----------------
(1)$\triangle ABC$において、$A=75^{ \circ },C=60^{ \circ },b=6$のとき、$C$の値を求めよ。
(2)動画内の図のような$\triangle ABC$において、辺$C$の大きさを求めよ。
この動画を見る
【数学】正弦定理の証明についての説明動画です
-----------------
(1)$\triangle ABC$において、$A=75^{ \circ },C=60^{ \circ },b=6$のとき、$C$の値を求めよ。
(2)動画内の図のような$\triangle ABC$において、辺$C$の大きさを求めよ。
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IA第2問〜三角比、データの分析
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#データの分析#三角比への応用(正弦・余弦・面積)#データの分析#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第2問}$
[1]$\triangle ABC$において、$BC=2\sqrt2$とする。$\angle ACB$の二等分線と辺$AB$の交点
を$D$とし、$CD=\sqrt2,\cos\angle BCD=\displaystyle\frac{3}{4}$とする。このとき、$BD=\boxed{\ \ ア\ \ }$
であり、
$\sin\angle ADC=\frac{\sqrt{\boxed{\ \ イウ\ \ }}}{\boxed{\ \ エ\ \ }}$
である。$\displaystyle\frac{AC}{AD}=\sqrt{\boxed{\ \ オ\ \ }}$ であるから
$AD=\boxed{\ \ カ\ \ }$
である。また、$\triangle ABC$の外接円の半径は$\displaystyle\frac{\boxed{\ \ キ\ \ }\sqrt{\boxed{\ \ ク\ \ }}}{\boxed{\ \ ケ\ \ }}$ である。
[2](1)次の$\boxed{\ \ コ\ \ },\boxed{\ \ サ\ \ }$に当てはまるものを、下の⓪~⑤のうちから
一つずつ選べ。ただし、解答の順序は問わない。
99個の観測地からなるデータがある。四分位数について述べた記述
で、どのようなデータでも成り立つものは$\boxed{\ \ コ\ \ }$と$\boxed{\ \ サ\ \ }$である。
⓪平均値は第1四分位数と第3四分位数の間にある。
①四分位範囲は標準偏差より大きい。
②中央値よりっ地裁観測地の個数は49個である。
③最大値に等しい観測値を1個削除しても第1四分位数は変わらない。
④第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地の個数は51個である。
⑤第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地からなるデータの範囲はもとの
データの四分位範囲に等しい。
(2)図1(※動画参照)は、平成27年の男の市区町村別平均寿命のデータを47の都道府県
P1,P2,$\cdots$,P47ごとに箱ひげ図にして、並べたものである。
次の$(\textrm{I}),(\textrm{II}),(\textrm{III})$は図1に関する記述である。
$(\textrm{I})$四分位範囲はどの都道府県においても1以下である。
$(\textrm{II})$箱ひげ図は中央値が小さい値から大きい値の順に上から
下へ並んである。
$(\textrm{III})$P1のデータのどの値とP47のデータのどの値とを
比較しても1.5以上の差がある。
次の$\boxed{\ \ シ\ \ }$に当てはまるものを、下の⓪~⑦のうちから一つ選べ。
$(\textrm{I}),(\textrm{II}),(\textrm{III})$の正誤の組み合わせとして正しいものは$\boxed{\ \ シ\ \ }$である。
(※選択肢は動画参照)
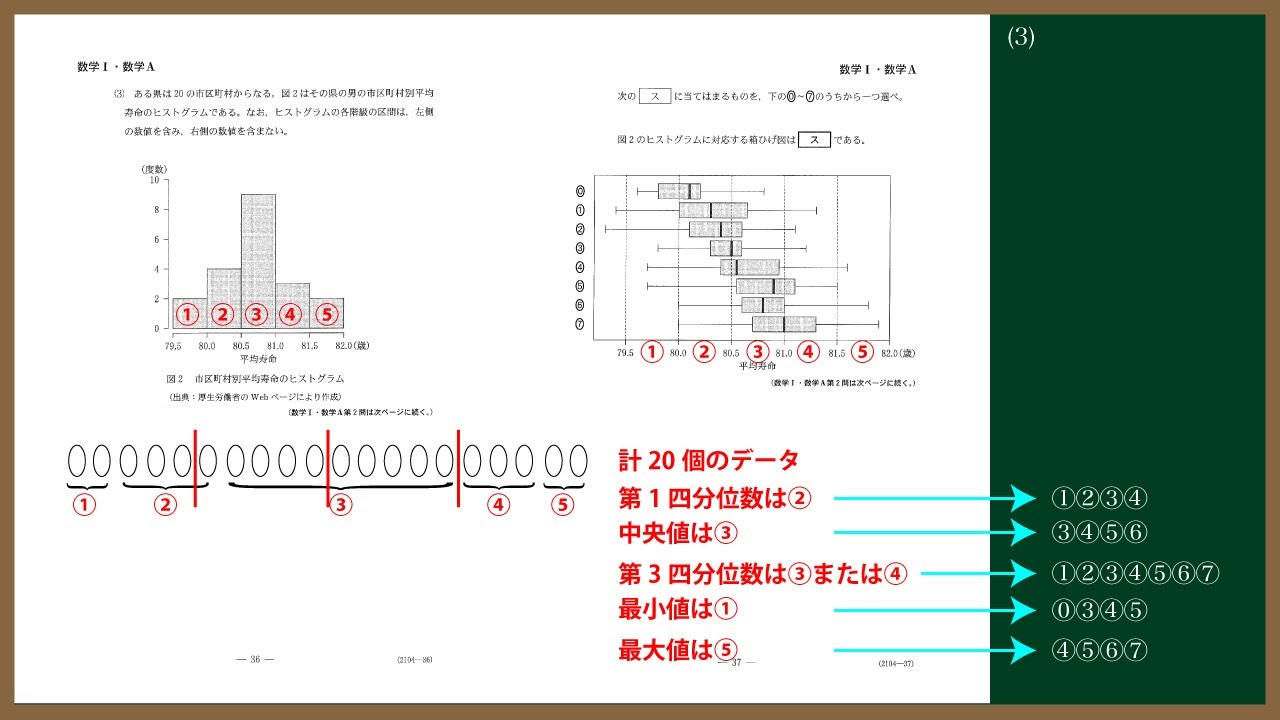
(3)ある県は20の市区町村からなる、図2(※動画参照)はその県の男の市区町村別平均
寿命のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を
含み、右側の数値を含まない。
次の$\boxed{\ \ ス\ \ }$に当てはまるものを、下の⓪~⑦のうちから一つ選べ。
図2のヒストグラムに対応する箱ひげ図は$\boxed{\ \ ス\ \ }$である。
(※選択肢は動画参照)
(4)図3(※動画参照)は、平成27年の男の都道府県別平均寿命と女の都道府県別平均
寿命の散布図である。2個の点が重なって区別できないところは黒丸にしている。
図には補助的に切片が5.5から7.5まで0.5刻みで傾き1の直線を5本付加している。
次の$\boxed{\ \ セ\ \ }$に当てはまるものを、下の⓪~③のうちから一つ選べ。
都道府県ごとに男女の平均寿命の差をとったデータに対するヒストグラム
は$\boxed{\ \ セ\ \ }$である。なお、ヒストグラムの各階級の区間は、
左側の数値を含み、右側の数値を含まない。
(※選択肢は動画参照)
2020センター試験過去問
この動画を見る
${\large第2問}$
[1]$\triangle ABC$において、$BC=2\sqrt2$とする。$\angle ACB$の二等分線と辺$AB$の交点
を$D$とし、$CD=\sqrt2,\cos\angle BCD=\displaystyle\frac{3}{4}$とする。このとき、$BD=\boxed{\ \ ア\ \ }$
であり、
$\sin\angle ADC=\frac{\sqrt{\boxed{\ \ イウ\ \ }}}{\boxed{\ \ エ\ \ }}$
である。$\displaystyle\frac{AC}{AD}=\sqrt{\boxed{\ \ オ\ \ }}$ であるから
$AD=\boxed{\ \ カ\ \ }$
である。また、$\triangle ABC$の外接円の半径は$\displaystyle\frac{\boxed{\ \ キ\ \ }\sqrt{\boxed{\ \ ク\ \ }}}{\boxed{\ \ ケ\ \ }}$ である。
[2](1)次の$\boxed{\ \ コ\ \ },\boxed{\ \ サ\ \ }$に当てはまるものを、下の⓪~⑤のうちから
一つずつ選べ。ただし、解答の順序は問わない。
99個の観測地からなるデータがある。四分位数について述べた記述
で、どのようなデータでも成り立つものは$\boxed{\ \ コ\ \ }$と$\boxed{\ \ サ\ \ }$である。
⓪平均値は第1四分位数と第3四分位数の間にある。
①四分位範囲は標準偏差より大きい。
②中央値よりっ地裁観測地の個数は49個である。
③最大値に等しい観測値を1個削除しても第1四分位数は変わらない。
④第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地の個数は51個である。
⑤第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地からなるデータの範囲はもとの
データの四分位範囲に等しい。
(2)図1(※動画参照)は、平成27年の男の市区町村別平均寿命のデータを47の都道府県
P1,P2,$\cdots$,P47ごとに箱ひげ図にして、並べたものである。
次の$(\textrm{I}),(\textrm{II}),(\textrm{III})$は図1に関する記述である。
$(\textrm{I})$四分位範囲はどの都道府県においても1以下である。
$(\textrm{II})$箱ひげ図は中央値が小さい値から大きい値の順に上から
下へ並んである。
$(\textrm{III})$P1のデータのどの値とP47のデータのどの値とを
比較しても1.5以上の差がある。
次の$\boxed{\ \ シ\ \ }$に当てはまるものを、下の⓪~⑦のうちから一つ選べ。
$(\textrm{I}),(\textrm{II}),(\textrm{III})$の正誤の組み合わせとして正しいものは$\boxed{\ \ シ\ \ }$である。
(※選択肢は動画参照)
(3)ある県は20の市区町村からなる、図2(※動画参照)はその県の男の市区町村別平均
寿命のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を
含み、右側の数値を含まない。
次の$\boxed{\ \ ス\ \ }$に当てはまるものを、下の⓪~⑦のうちから一つ選べ。
図2のヒストグラムに対応する箱ひげ図は$\boxed{\ \ ス\ \ }$である。
(※選択肢は動画参照)
(4)図3(※動画参照)は、平成27年の男の都道府県別平均寿命と女の都道府県別平均
寿命の散布図である。2個の点が重なって区別できないところは黒丸にしている。
図には補助的に切片が5.5から7.5まで0.5刻みで傾き1の直線を5本付加している。
次の$\boxed{\ \ セ\ \ }$に当てはまるものを、下の⓪~③のうちから一つ選べ。
都道府県ごとに男女の平均寿命の差をとったデータに対するヒストグラム
は$\boxed{\ \ セ\ \ }$である。なお、ヒストグラムの各階級の区間は、
左側の数値を含み、右側の数値を含まない。
(※選択肢は動画参照)
2020センター試験過去問
