 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
sin cos
cos36°🟰❓
cos36°🟰❓

cos36°🟰❓

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
次の値を求めよ
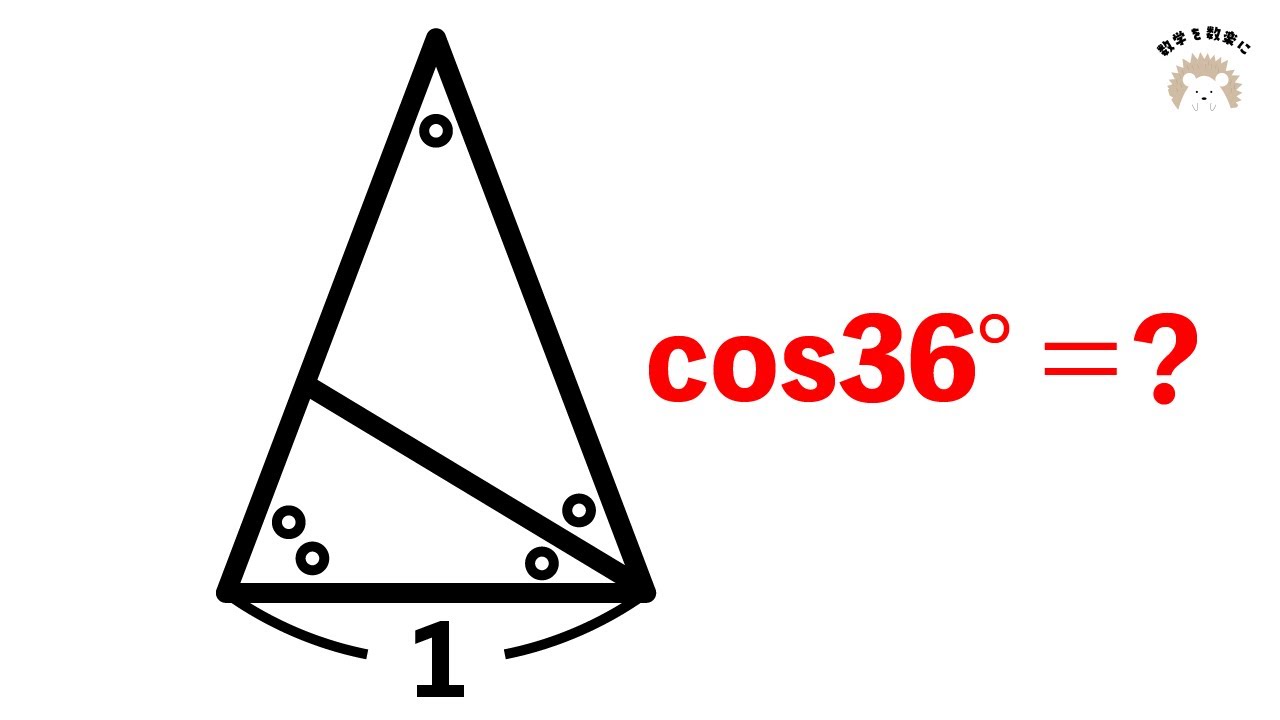
$\cos{36^{\circ}}=?$
この動画を見る
次の値を求めよ
$\cos{36^{\circ}}=?$
平方根 式の値 立教新座
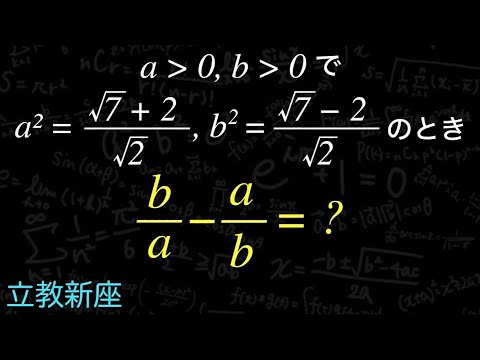
単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a \gt 0,b \gt 0で
a^{ 2 }=\dfrac{\sqrt{ 7 }+2}{\sqrt{ 2 }},b^{ 2 }=\dfrac{\sqrt{ 7 }-2}{\sqrt{ 2 }}のとき、
\dfrac{b}{a}-\dfrac{a}{b}=$?
この動画を見る
$a \gt 0,b \gt 0で
a^{ 2 }=\dfrac{\sqrt{ 7 }+2}{\sqrt{ 2 }},b^{ 2 }=\dfrac{\sqrt{ 7 }-2}{\sqrt{ 2 }}のとき、
\dfrac{b}{a}-\dfrac{a}{b}=$?
これできる?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
これできる?
※問題文は動画内参照
この動画を見る
これできる?
※問題文は動画内参照
福田の数学〜明治大学2024全学部統一IⅡAB第1問(4)〜図形の計量
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
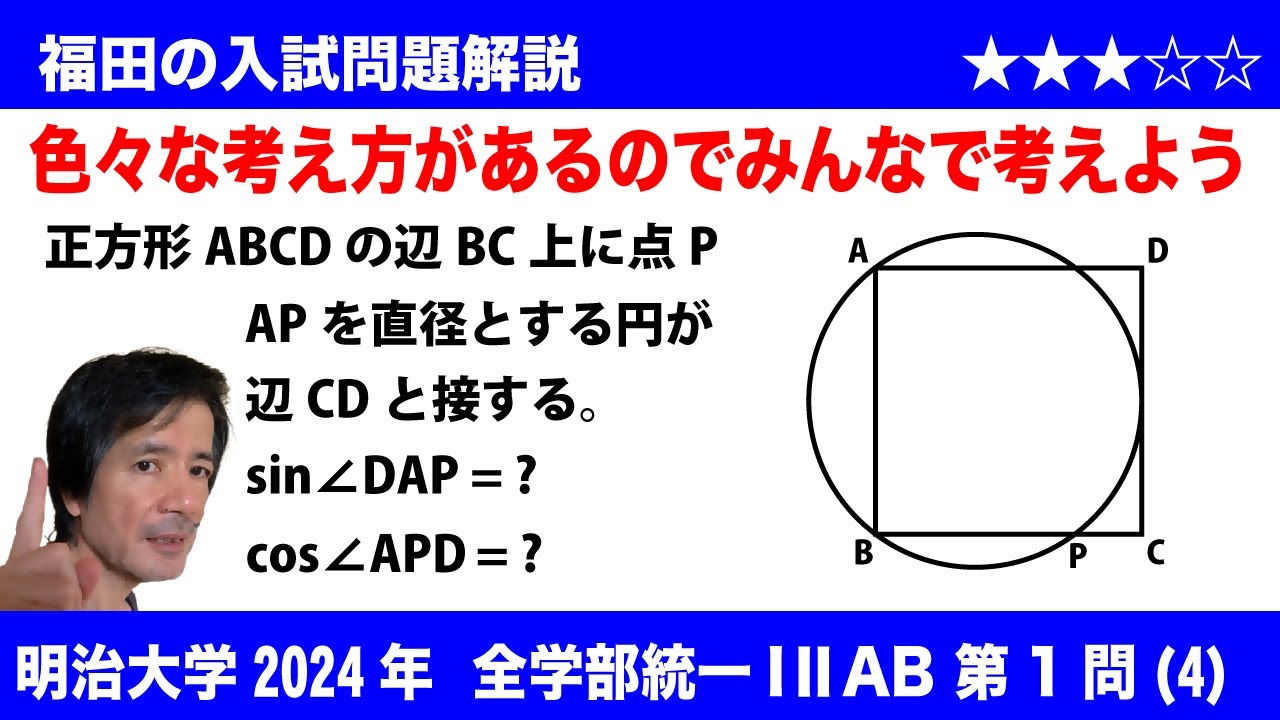
平面上に正方形ABCD (※図は動画内参照) がある。点Pが辺BC上にあり、線分APを直径とする円が辺CDと接するものとする。このとき $\cos{\angle\mathrm{DAP}}=\frac{\fbox{セ}}{\fbox{ソ}}$ であり、また $\sin{\angle\mathrm{APD}}=\frac{\fbox{タチ}\sqrt{\fbox{ツテ}}}{\fbox{トナ}}$ である。
この動画を見る
平面上に正方形ABCD (※図は動画内参照) がある。点Pが辺BC上にあり、線分APを直径とする円が辺CDと接するものとする。このとき $\cos{\angle\mathrm{DAP}}=\frac{\fbox{セ}}{\fbox{ソ}}$ であり、また $\sin{\angle\mathrm{APD}}=\frac{\fbox{タチ}\sqrt{\fbox{ツテ}}}{\fbox{トナ}}$ である。
福田の数学〜明治大学2024全学部統一IⅡAB第1問(3)〜平均と分散

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次のデータは、ある7人制ラグビーチームの7人の選手の身長を調べたものである。
$181,\,185,\,184,\,176,\,172,\,x,\,y$
このデータの平均が$177$、分散が$40$のとき、$x < y$ とすると$x=\fbox{シ},\,y=\fbox{ス}$である。
この動画を見る
次のデータは、ある7人制ラグビーチームの7人の選手の身長を調べたものである。
$181,\,185,\,184,\,176,\,172,\,x,\,y$
このデータの平均が$177$、分散が$40$のとき、$x < y$ とすると$x=\fbox{シ},\,y=\fbox{ス}$である。
#自治医科大学2024#式変形_21#元高校教員

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算(整式・展開・因数分解)#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$x^{\frac{1}{3}}+x^{-\frac{1}{3}}$のとき
$\displaystyle \frac{x+x^{-1}}{2}$の値を求めよ。
出典:自治医科大学 式変形問題
この動画を見る
$x^{\frac{1}{3}}+x^{-\frac{1}{3}}$のとき
$\displaystyle \frac{x+x^{-1}}{2}$の値を求めよ。
出典:自治医科大学 式変形問題
よく間違える二次関数の変域

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$-1\leqq x\leqq 2$のとき、$x^2$の範囲を求めよ。
この動画を見る
$-1\leqq x\leqq 2$のとき、$x^2$の範囲を求めよ。
福田の数学〜中央大学2024理工学部第1問〜3つの関数の大小関係と絶対不等式

単元:
#数Ⅰ#2次関数#2次関数とグラフ#微分とその応用#積分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
この動画を見る
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
#福島大学2024#元高校教員

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
ますただ
問題文全文(内容文):
$\sqrt{ 2023\times2025+1 }$の値を求めよ。
出典:2024年福島大学
この動画を見る
$\sqrt{ 2023\times2025+1 }$の値を求めよ。
出典:2024年福島大学
ポイントは実数 摂南大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-6xy+10y^2-6y+9=0$
$x=? y=?$
(ただし、$x,y$は実数)
この動画を見る
$x^2-6xy+10y^2-6y+9=0$
$x=? y=?$
(ただし、$x,y$は実数)
ポイントは実数 摂南大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-6xy+10y^2-6y+9=0$
のときの$x,y$を求めよ。
$(ただしx,yは実数)$
この動画を見る
$x^2-6xy+10y^2-6y+9=0$
のときの$x,y$を求めよ。
$(ただしx,yは実数)$
大学入試問題#901「基本だけど初手大事」 #電気通信大学(2024)

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \sqrt{ 2-\sqrt{ x} }$ $dx$
出典:2024年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{4} \sqrt{ 2-\sqrt{ x} }$ $dx$
出典:2024年電気通信大学
2次方程式の応用 (高校数学)

単元:
#2次関数#2次方程式と2次不等式#2次関数とグラフ
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式 $(x-l) (x-2) -(x-k) =0$ の解を $\alpha, \beta (\alpha<\beta)$ とするとき、$\alpha, \beta, 1, 2, k$ を小さい順に並べよ(ただし、$1<k<2$)
この動画を見る
2次方程式 $(x-l) (x-2) -(x-k) =0$ の解を $\alpha, \beta (\alpha<\beta)$ とするとき、$\alpha, \beta, 1, 2, k$ を小さい順に並べよ(ただし、$1<k<2$)
2次方程式の応用 (高校数学)

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$(x-1)(x-2)-(x-k)=0の解を\mathit{α ,β}(\mathit{α}<\mathit{β})とするとき
\mathit{α,β},1,2,kを小さい順に並べよ。(ただし、1<\mathit{k}<2$)
この動画を見る
2次方程式$(x-1)(x-2)-(x-k)=0の解を\mathit{α ,β}(\mathit{α}<\mathit{β})とするとき
\mathit{α,β},1,2,kを小さい順に並べよ。(ただし、1<\mathit{k}<2$)
福田の数学〜中央大学2024経済学部第1問(2)〜集合の要素の個数

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
この動画を見る
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
【数学】中高一貫校用問題集数式・関数編:2次関数の決定

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)$x^2$の係数が2で、そのグラフが点(1,3)を通り、頂点が直線$y=2x-3$上にあるような2次関数を求めよ。
(2)2次関数$y=x^2-2ax+b$のグラフが点(1,3)を通り、頂点が直線$y=x-10$上にあるとき、定数a,bの値を求めよ。
(3)2次関数$y=2x^2+ax+b$のグラフが点(3,5)を通り、頂点が直線$y=2x-5$上にあるとき、定数a,bの値を求めよ。
この動画を見る
次の問いに答えよ。
(1)$x^2$の係数が2で、そのグラフが点(1,3)を通り、頂点が直線$y=2x-3$上にあるような2次関数を求めよ。
(2)2次関数$y=x^2-2ax+b$のグラフが点(1,3)を通り、頂点が直線$y=x-10$上にあるとき、定数a,bの値を求めよ。
(3)2次関数$y=2x^2+ax+b$のグラフが点(3,5)を通り、頂点が直線$y=2x-5$上にあるとき、定数a,bの値を求めよ。
福田の数学〜中央大学2024経済学部第1問(1)〜絶対値の付いた2次不等式の解

まず二乗したものを求める

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=2+\sqrt{3} \\
b^2=2-\sqrt{3}
\end{array}
\right.
\end{eqnarray}
$
のとき、$ab$の値を求めよ
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=2+\sqrt{3} \\
b^2=2-\sqrt{3}
\end{array}
\right.
\end{eqnarray}
$
のとき、$ab$の値を求めよ
連立方程式 2通りで解説!! コメント欄に訂正あり。

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
次の連立方程式を解け
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy=2 \\
yz=6 \\
zx=3
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の連立方程式を解け
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy=2 \\
yz=6 \\
zx=3
\end{array}
\right.
\end{eqnarray}$
最大値=❓ 分数関数 (高校数学)

中学生にはきついよ 因数分解 東京農大一

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#東京農工大学
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$4a^4b^4-29a^2b^2+25$
この動画を見る
因数分解せよ
$4a^4b^4-29a^2b^2+25$
【高校入試では珍しい…!】二次方程式:函館ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#数と式#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$kx^2-6x+1=0 の解の個数が1個となるようなkの値を2個求めなさい。$
この動画を見る
$kx^2-6x+1=0 の解の個数が1個となるようなkの値を2個求めなさい。$
√の中に8がいっぱい!!
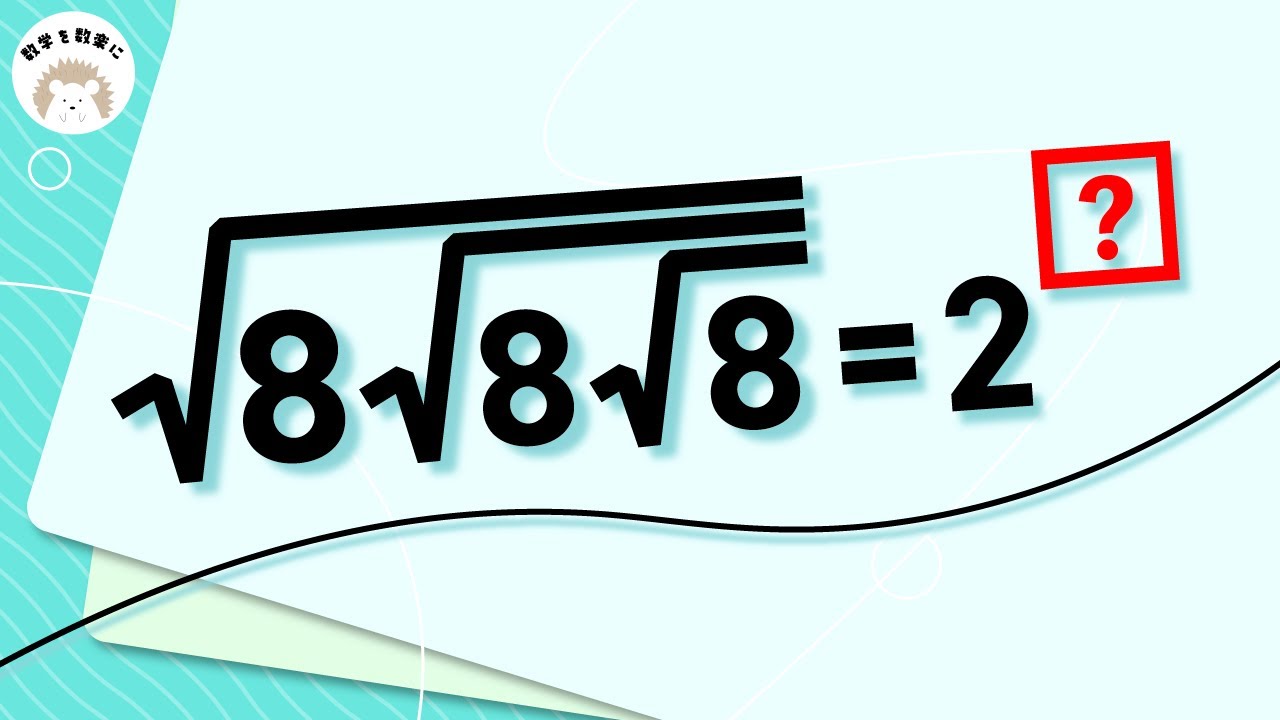
単元:
#数Ⅰ#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#指数関数
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{8\sqrt{8\sqrt8}}=2$
この動画を見る
$\sqrt{8\sqrt{8\sqrt8}}=2$
福田のおもしろ数学210〜2つ対称式の条件から和を求める

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算(整式・展開・因数分解)#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
この動画を見る
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
単元:
#数Ⅰ#情報Ⅰ(高校生)#データの分析#データの分析#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
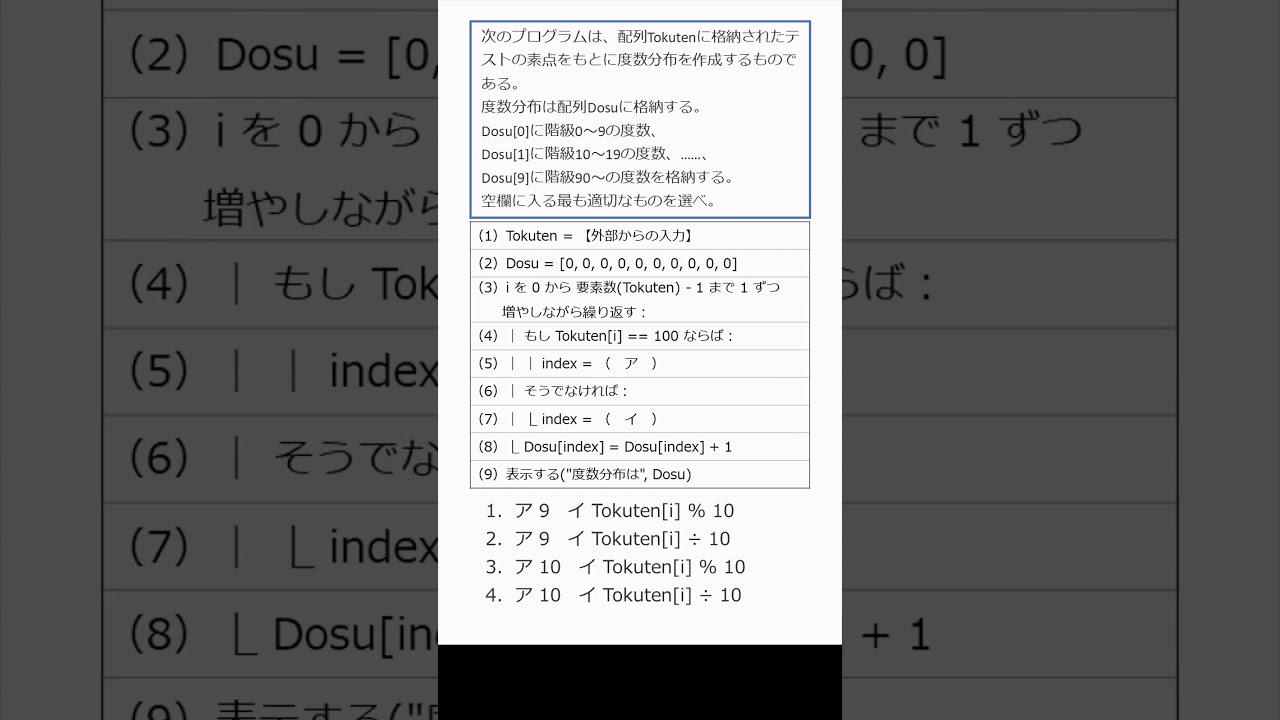
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
【問題文】
次のプログラムは、配列 Tokutenに格納されたテストの素点をもとに、度数分布を作成するものである。
度数分布は配列 度数に格納する。
度数[0]に階級0~9の度数、度数[1]に階級10~19の度数、……、度数[9]に階級90~の度数を格納する。
空欄に入る最も適切なものを選べ。
この動画を見る
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
【問題文】
次のプログラムは、配列 Tokutenに格納されたテストの素点をもとに、度数分布を作成するものである。
度数分布は配列 度数に格納する。
度数[0]に階級0~9の度数、度数[1]に階級10~19の度数、……、度数[9]に階級90~の度数を格納する。
空欄に入る最も適切なものを選べ。
最後まで油断するなよ因数分解

最後まで油断するなよ因数分解

