 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
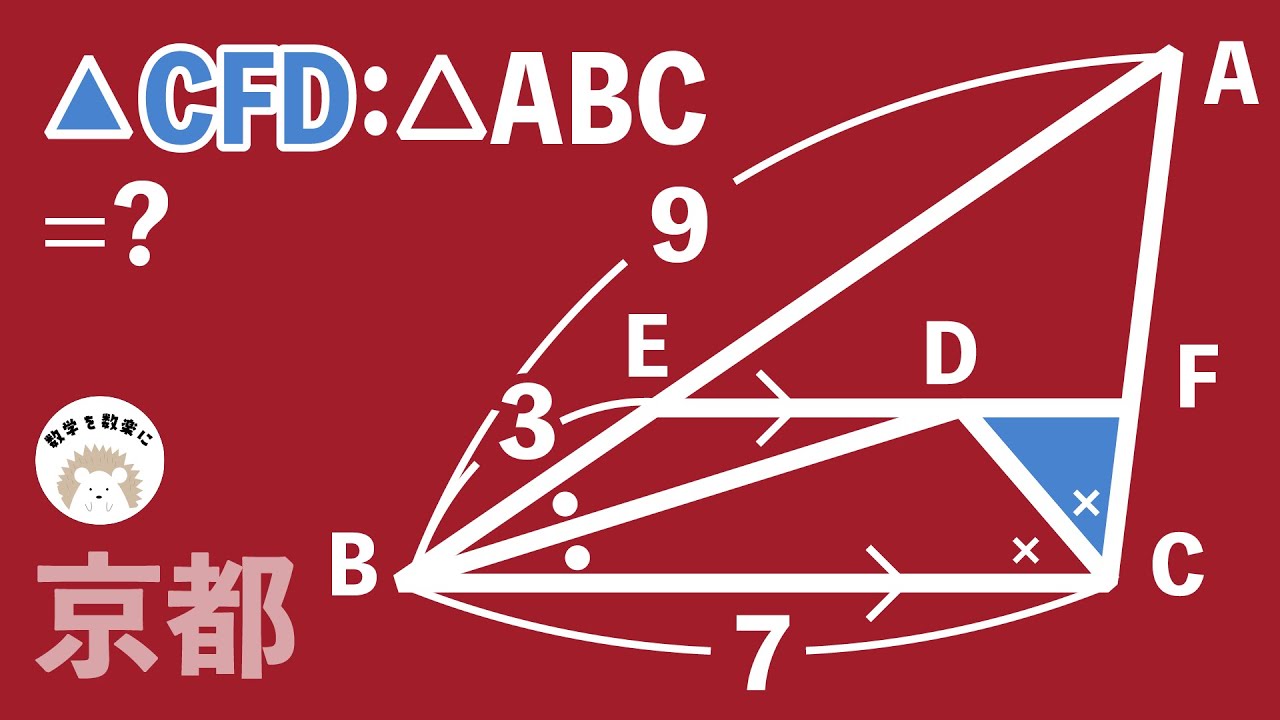
クイズノックもノックアウト!? 面積比 京都府
難しい因数分解やろうぜ【高校数学】

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
難しい因数分解
(1)$a(l^2-c^2)+l(c^2-a^2)+c(a^2-l^2)$
(2)$a^2(b+c)+b^2(c+a)+c^2(a+b)+2abc$
(3)$2x^2+5xy+2y^2-x+y-1$
(4)$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$
(5)$x^2-y^2-zx+yz$
(6)$a(b+c)^2+b(c+a)^2+c(a+b)^2-4abc$
この動画を見る
難しい因数分解
(1)$a(l^2-c^2)+l(c^2-a^2)+c(a^2-l^2)$
(2)$a^2(b+c)+b^2(c+a)+c^2(a+b)+2abc$
(3)$2x^2+5xy+2y^2-x+y-1$
(4)$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$
(5)$x^2-y^2-zx+yz$
(6)$a(b+c)^2+b(c+a)^2+c(a+b)^2-4abc$
超不人気!確率漸化式だよ

単元:
#数Ⅰ#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
点Pは原点を出発して確率$p(0\leqq P\leqq 1)$で$+1$, $1-p$で$+2$進む.
自然数nの地点に到達する確率$P_n$を求めよ.
大阪教育大過去問
この動画を見る
点Pは原点を出発して確率$p(0\leqq P\leqq 1)$で$+1$, $1-p$で$+2$進む.
自然数nの地点に到達する確率$P_n$を求めよ.
大阪教育大過去問
図形と計量 三角比の相互関係の利用2 【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sin^4\theta-\cos^4\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
この動画を見る
$\sin^4\theta-\cos^4\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
図形と計量 三角比の相互関係の利用【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
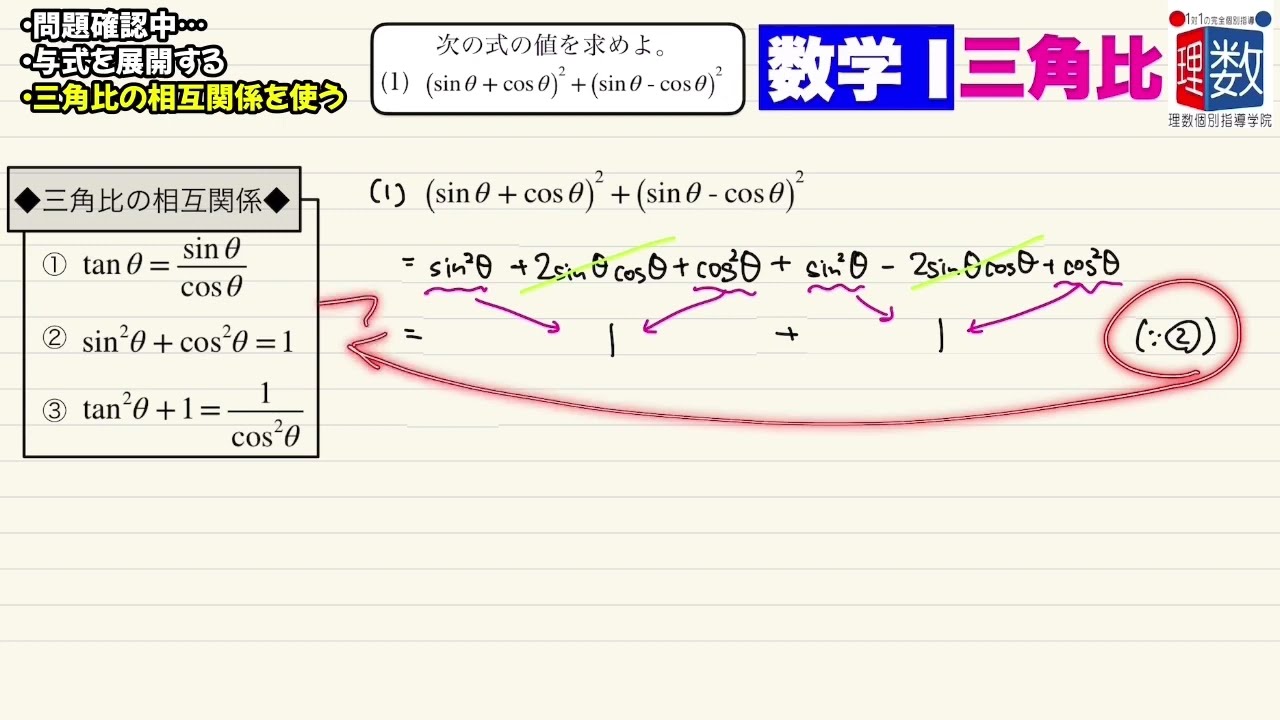
次の式の値を求めよ。
(1)$(\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2$
(2)$(1-\sin\theta)(1+\sin\theta)-\dfrac{1}{1+\tan^2\theta}$
この動画を見る
次の式の値を求めよ。
(1)$(\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2$
(2)$(1-\sin\theta)(1+\sin\theta)-\dfrac{1}{1+\tan^2\theta}$
図形と計量 有名角以外を含む三角比計算【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
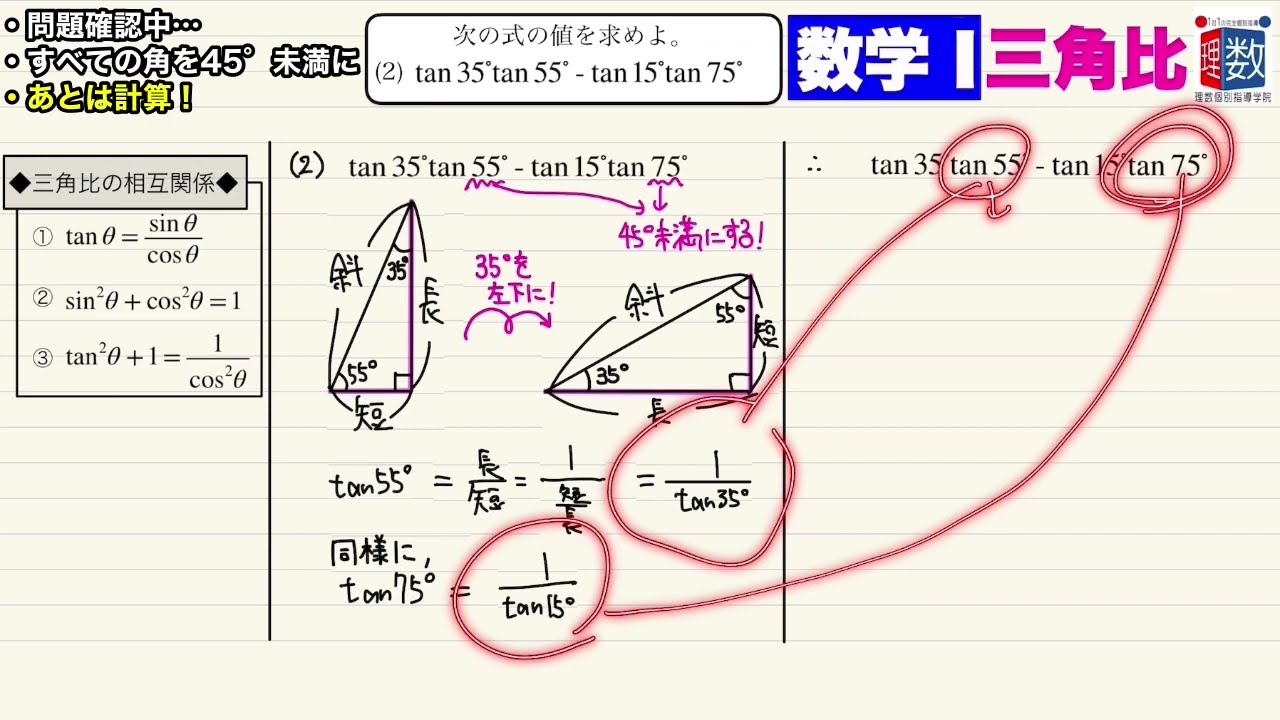
次の式の値を求めよ。
(1) $\sin^240°+\sin^250°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^250°$
この動画を見る
次の式の値を求めよ。
(1) $\sin^240°+\sin^250°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^250°$
福田の数学〜東北大学2023年文系第3問〜軸の動く最大最小

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
【スムーズに!スマートに!】一次方程式:関西大倉高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.
関西大倉高校過去問
この動画を見る
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.
関西大倉高校過去問
福田の数学〜東北大学2023年文系第1問〜三角形の面積と内接円と外接円の半径
単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#三角関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
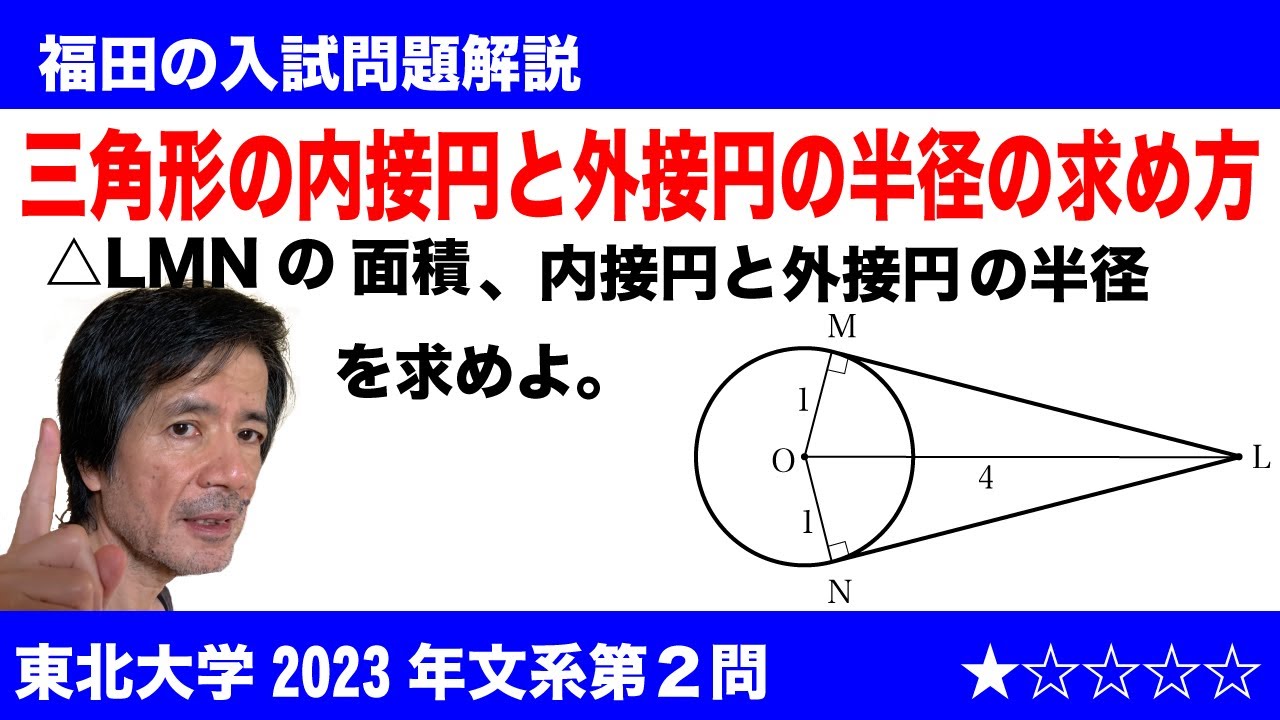
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
筆算不要!!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {999 \times 997 +1}$
この動画を見る
$\sqrt {999 \times 997 +1}$
【数検準2級】高校数学:数学検定準2級2次:問5

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問5. 次の問いに答えなさい。
(7) 地点Aから、湖を隔てた地点Bまでの距離を測定するために、地点Aから100m、地点Bから60m離れたところに地点Pをとります。地点Pから地点A、Bをみて$\angle APB$の大きさを調べたところ、$\angle APB=120°$でした。
このとき、2地点A、B間の距離は何mですか。余弦定理を用いて求めなさい。
この動画を見る
問5. 次の問いに答えなさい。
(7) 地点Aから、湖を隔てた地点Bまでの距離を測定するために、地点Aから100m、地点Bから60m離れたところに地点Pをとります。地点Pから地点A、Bをみて$\angle APB$の大きさを調べたところ、$\angle APB=120°$でした。
このとき、2地点A、B間の距離は何mですか。余弦定理を用いて求めなさい。
シンプルだけど気付きにくい 円の問題 筑波大附属
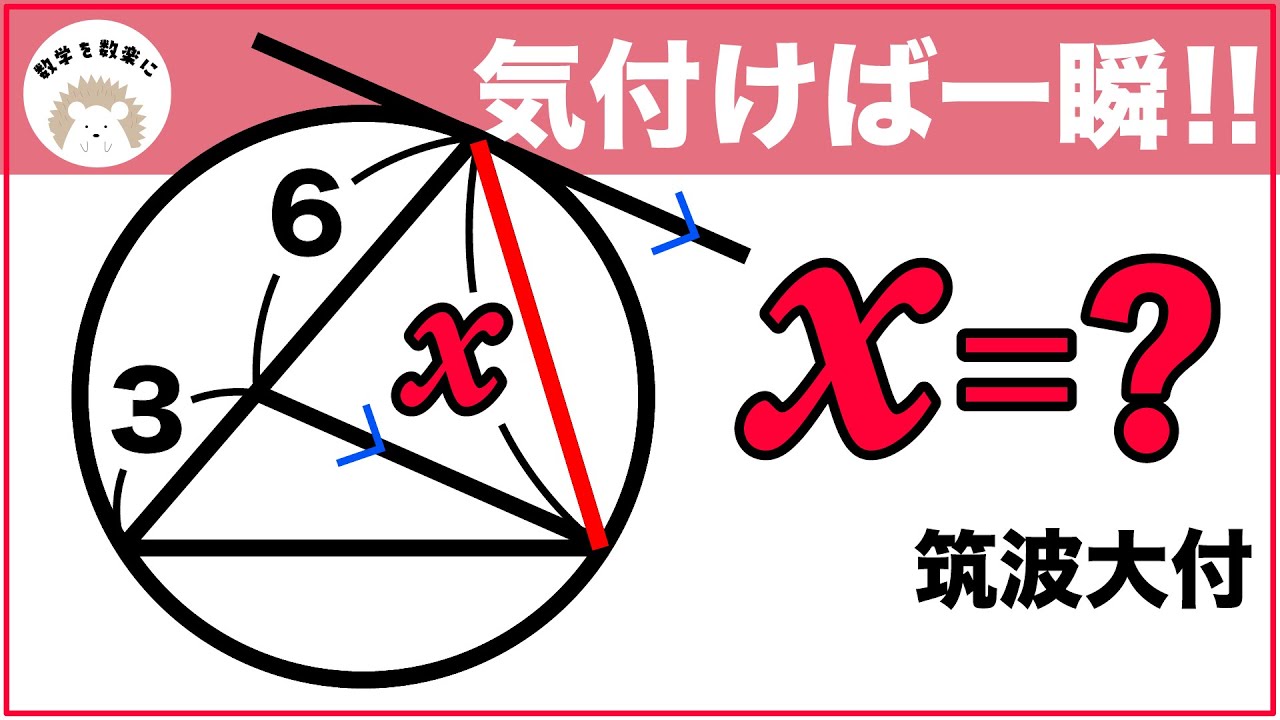
式の値 早稲田実業

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
この動画を見る
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
絶対値を含む方程式
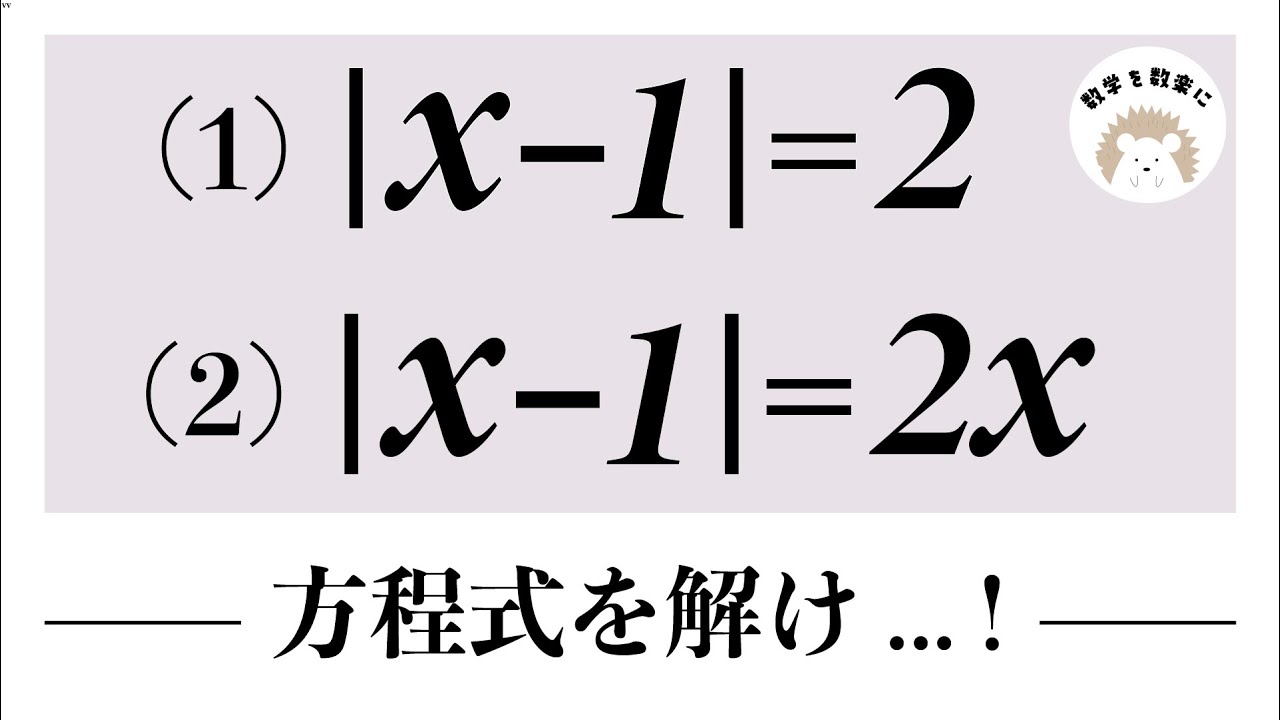
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
この動画を見る
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
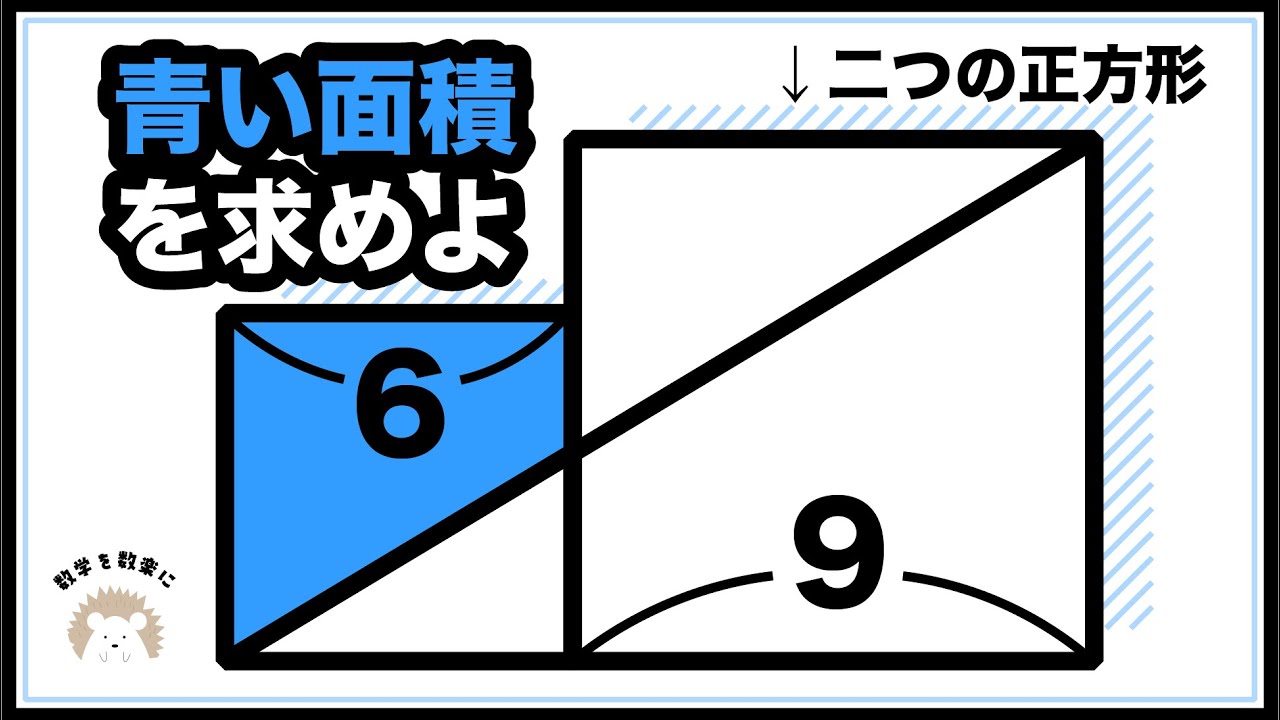
2つの正方形
6乗−6乗の因数分解

ハートで分けろ 高校数学 式の値
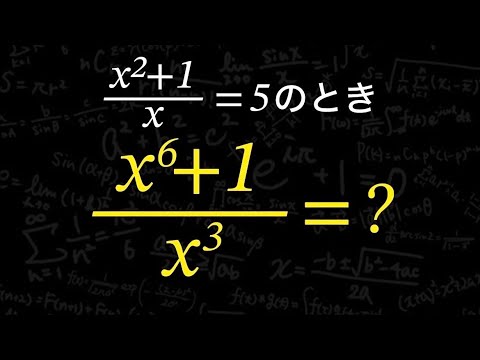
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$
この動画を見る
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$
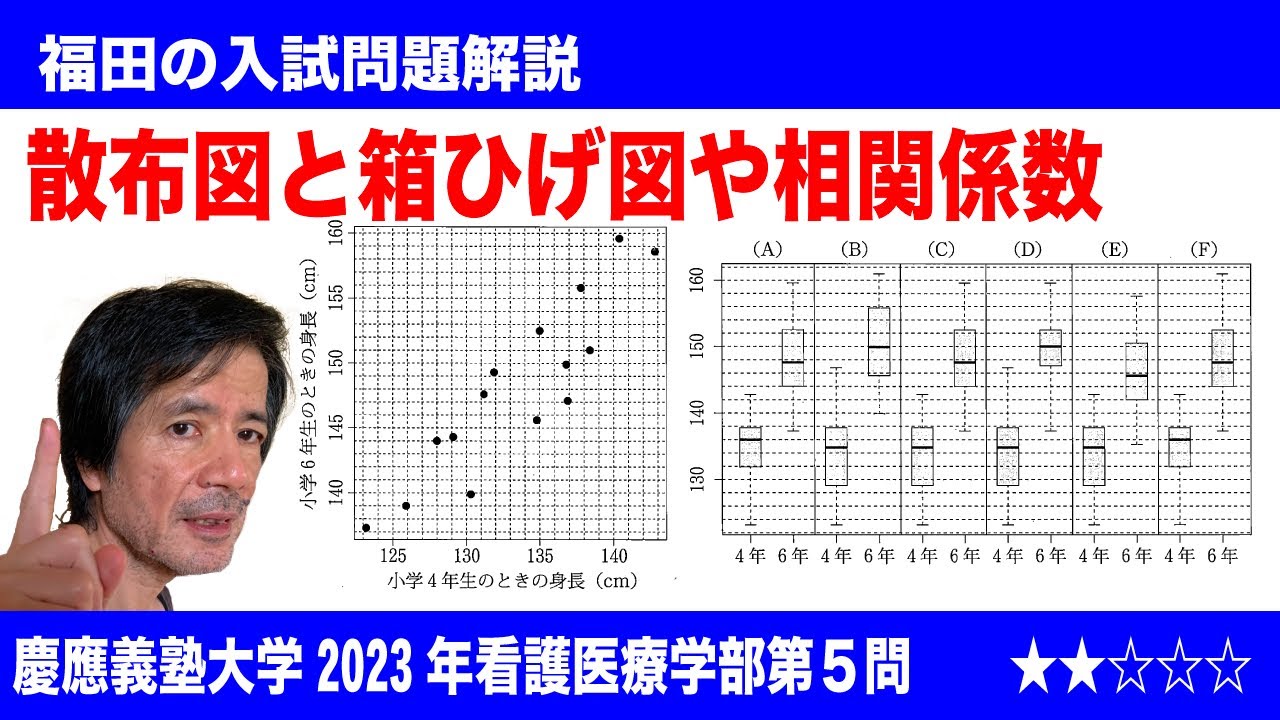
福田の数学〜慶應義塾大学2023年看護医療学部第5問〜散布図と箱ひげ図の関係と相関係数
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
工夫して解こうよ!平方根の計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(\sqrt 3 + 1)^2}{\sqrt 2} + \frac{(\sqrt 6 - \sqrt 2 )^2}{2 \sqrt 2}$
滝高等学校
この動画を見る
$\frac{(\sqrt 3 + 1)^2}{\sqrt 2} + \frac{(\sqrt 6 - \sqrt 2 )^2}{2 \sqrt 2}$
滝高等学校
【数検準2級】高校数学:数学検定準2級2次:問4

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問4. a,bを定数とします。放物線$y=-x^2+4ax+b$ について、次の問いに答えなさい。
(5) 頂点の座標をa,bを用いて表しなさい。この問題は答えだけを書いてください。
(6) 放物線 $y=-x^2$ をx軸方向に1、y軸方向に5だけ平行移動したところ、上の放物線になりました。このとき、a,bの値をそれぞれ求めなさい。
この動画を見る
問4. a,bを定数とします。放物線$y=-x^2+4ax+b$ について、次の問いに答えなさい。
(5) 頂点の座標をa,bを用いて表しなさい。この問題は答えだけを書いてください。
(6) 放物線 $y=-x^2$ をx軸方向に1、y軸方向に5だけ平行移動したところ、上の放物線になりました。このとき、a,bの値をそれぞれ求めなさい。
tan1°✖️ tan2°✖️tan3°✖️・・・✖️tan89°

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$tan1^ \circ \times tan2^ \circ \times tan3^ \circ \times \cdots tan88^ \circ \times tan89^ \circ$
この動画を見る
$tan1^ \circ \times tan2^ \circ \times tan3^ \circ \times \cdots tan88^ \circ \times tan89^ \circ$
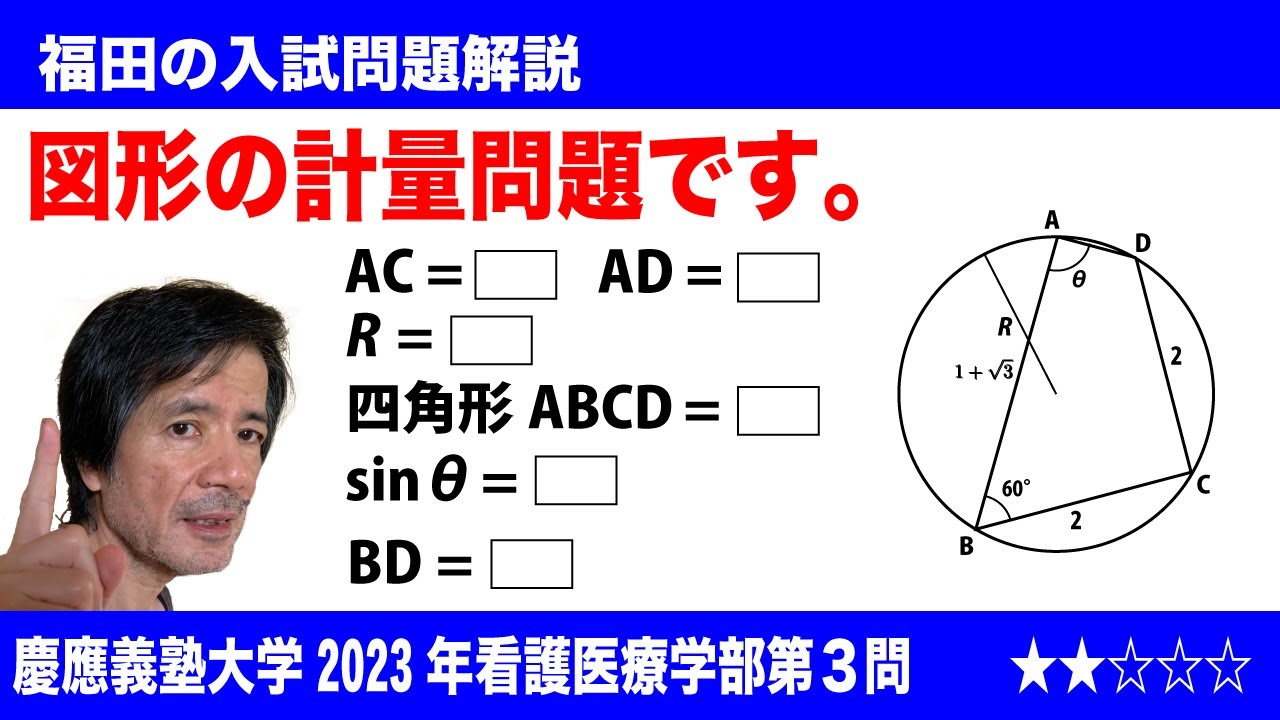
福田の数学〜慶應義塾大学2023年看護医療学部第3問〜三角比と図形の計量
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 半径Rの円に内接する四角形ABCDにおいて
AB=1+$\sqrt3$, BC=CD=2, $\angle$ABC=60°
であるとき、$\angle$ADCの大きさは$\angle$ADC=$\boxed{\ \ ソ\ \ }$であり、AC,AD,Rの長さはそれぞれAC=$\boxed{\ \ タ\ \ }$, AD=$\boxed{\ \ チ\ \ }$, R=$\boxed{\ \ ツ\ \ }$である。
また、四角形ABCDの面積は$\boxed{\ \ テ\ \ }$である。さらに、θ=$\angle$DABとするとき、$\sin\theta$=$\boxed{\ \ ト\ \ }$であり、BDの長さはBD=$\boxed{\ \ ナ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{3}$ 半径Rの円に内接する四角形ABCDにおいて
AB=1+$\sqrt3$, BC=CD=2, $\angle$ABC=60°
であるとき、$\angle$ADCの大きさは$\angle$ADC=$\boxed{\ \ ソ\ \ }$であり、AC,AD,Rの長さはそれぞれAC=$\boxed{\ \ タ\ \ }$, AD=$\boxed{\ \ チ\ \ }$, R=$\boxed{\ \ ツ\ \ }$である。
また、四角形ABCDの面積は$\boxed{\ \ テ\ \ }$である。さらに、θ=$\angle$DABとするとき、$\sin\theta$=$\boxed{\ \ ト\ \ }$であり、BDの長さはBD=$\boxed{\ \ ナ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
データの分析 データが変更されたときの平均、分散の関係【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
この動画を見る
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
2024を素因数分解

データの分析 平均と分散だけ与えられたデータ【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
20個の値からなるデータがあり、そのうちの8個の値の平均値は3,分散は4、残りの12個の値の平均値は8、分散は9である。
(1)このデータの平均値を求めよ。
(2)このデータの分散を求めよ。
この動画を見る
20個の値からなるデータがあり、そのうちの8個の値の平均値は3,分散は4、残りの12個の値の平均値は8、分散は9である。
(1)このデータの平均値を求めよ。
(2)このデータの分散を求めよ。
福田の数学〜慶應義塾大学2023年看護医療学部第2問(2)〜ルートが自然数になる条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
2=3
数と式 真偽の調べ方【いつものシミズ君がていねいに解説】

単元:
#数Ⅰ#数と式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,bは実数とする。次の命題の真偽を求めよ。
(1)$ab=0$ならば$a^2+b^2=0$である。
(2)$a^2=4$ならば$\vert a+1\vert \geqq 1$である。
(3)$ab$が有理数であるならば、a、bはともに有理数である。
(4)$a+b、ab$がともに有理数ならば、a、bはともに有理数である。
全体集合を$U$とし、条件$p、q$を満たす全体の集合を、それぞれ$P.Q$とする。
命題$p$(補集合)⇒$q$が真であるとき、$P、Q$について常に成り立つ事をすべて選べ。
①$P=Q$
②$Q⊂P$
③$Q$(補集合)$⊂P$
④$P⊂Q$(補集合)
⑤$P∪Q$(補集合)$=P$
⑥$P∪Q$(補集合)$=Q$(補集合)
⑦$P∩Q=∅$
⑧$P∪Q=U$
この動画を見る
a,bは実数とする。次の命題の真偽を求めよ。
(1)$ab=0$ならば$a^2+b^2=0$である。
(2)$a^2=4$ならば$\vert a+1\vert \geqq 1$である。
(3)$ab$が有理数であるならば、a、bはともに有理数である。
(4)$a+b、ab$がともに有理数ならば、a、bはともに有理数である。
全体集合を$U$とし、条件$p、q$を満たす全体の集合を、それぞれ$P.Q$とする。
命題$p$(補集合)⇒$q$が真であるとき、$P、Q$について常に成り立つ事をすべて選べ。
①$P=Q$
②$Q⊂P$
③$Q$(補集合)$⊂P$
④$P⊂Q$(補集合)
⑤$P∪Q$(補集合)$=P$
⑥$P∪Q$(補集合)$=Q$(補集合)
⑦$P∩Q=∅$
⑧$P∪Q=U$
数と式 集合の考え方【いつものシミズ君がていねいに解説】

単元:
#数Ⅰ#数と式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。$U$の部分集合A、Bについて
$A∩B={2}$ $A$(補集合)$∩B={4,6,8}$ $A$(補集合)$∩B$(補集合)$={1.9}$
であるとき、次の$∩$を求めよ。
(1)$A∪B$
(2)$B$
(3)$A∩B$(補集合)
$U={x|1≦x≦10、xは整数}$を全体集合とする。$U$の部分集合
$A={1,2,3,4,8},B={3,4,5,6},C{2,3,6,7}$
について、次の集合を求めよ。
(1)$A∩B∩C$
(2)$A∪B∪C$
(3)$A∩B∩C$(補集合)
(4)$A$(補集合)$∩B∩C$(補集合)
(5)$(A∩B∩C)$(補集合)
(6)$(A∪C)∩B$(補集合)
$A={1、3、3a-2}$, $B={-5、a+2、a^2-2a+1}$,$A∩B={1、4}$のとき
定数aの値と和集合$A∪B$を求めよ。
この動画を見る
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。$U$の部分集合A、Bについて
$A∩B={2}$ $A$(補集合)$∩B={4,6,8}$ $A$(補集合)$∩B$(補集合)$={1.9}$
であるとき、次の$∩$を求めよ。
(1)$A∪B$
(2)$B$
(3)$A∩B$(補集合)
$U={x|1≦x≦10、xは整数}$を全体集合とする。$U$の部分集合
$A={1,2,3,4,8},B={3,4,5,6},C{2,3,6,7}$
について、次の集合を求めよ。
(1)$A∩B∩C$
(2)$A∪B∪C$
(3)$A∩B∩C$(補集合)
(4)$A$(補集合)$∩B∩C$(補集合)
(5)$(A∩B∩C)$(補集合)
(6)$(A∪C)∩B$(補集合)
$A={1、3、3a-2}$, $B={-5、a+2、a^2-2a+1}$,$A∩B={1、4}$のとき
定数aの値と和集合$A∪B$を求めよ。
tan30° =❓ tan15°=❓
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
tan30°=
tan15°=
*図は動画内参照
この動画を見る
tan30°=
tan15°=
*図は動画内参照
