 空間における垂直と平行と多面体(オイラーの法則)
空間における垂直と平行と多面体(オイラーの法則)
 空間における垂直と平行と多面体(オイラーの法則)
空間における垂直と平行と多面体(オイラーの法則)
福田のおもしろ数学507〜三角形の面がm個ありどの頂点にも4本の辺が集まる多面体

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある凸多面体において、
三角形の面が$m$枚あり、
(他の形の面も含まれている可能性がある)
すべての頂点にはちょうど$4$枚の辺が集まって
いるとする。
このとき、$m$の最小値を求めて下さい。
この動画を見る
ある凸多面体において、
三角形の面が$m$枚あり、
(他の形の面も含まれている可能性がある)
すべての頂点にはちょうど$4$枚の辺が集まって
いるとする。
このとき、$m$の最小値を求めて下さい。
福田のおもしろ数学433〜四面体に関する計量問題
単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
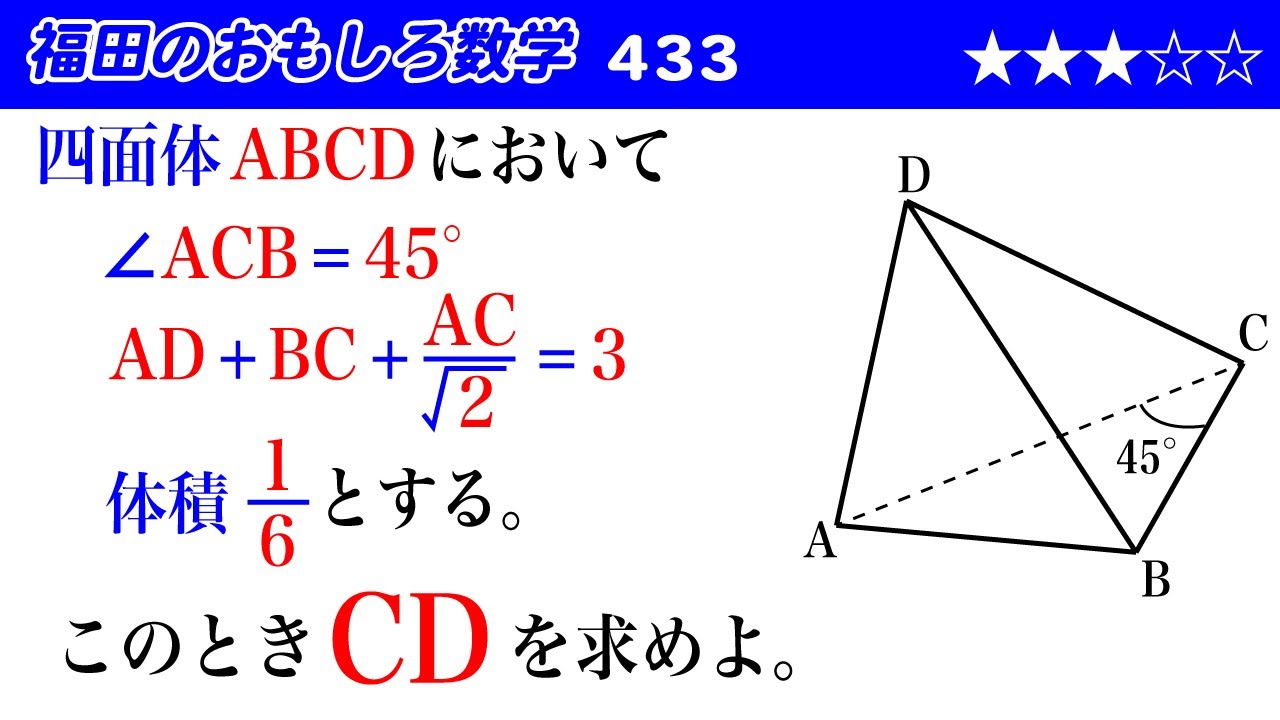
四面体$ABCD$において
$\angle ACB=45°$
$AD+BC+\dfrac{AC}{\sqrt2}=3$
体積$\dfrac{1}{6}$とする。
このとき$CD$を求めよ。
図は動画内参照
この動画を見る
四面体$ABCD$において
$\angle ACB=45°$
$AD+BC+\dfrac{AC}{\sqrt2}=3$
体積$\dfrac{1}{6}$とする。
このとき$CD$を求めよ。
図は動画内参照
これなに?

これ知ってる?

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
正四面体の体積を一瞬で出す方法を解説していきます.
この動画を見る
正四面体の体積を一瞬で出す方法を解説していきます.
福田のおもしろ数学034〜各面が合同な三角形でできた四面体の体積〜等面四面体
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
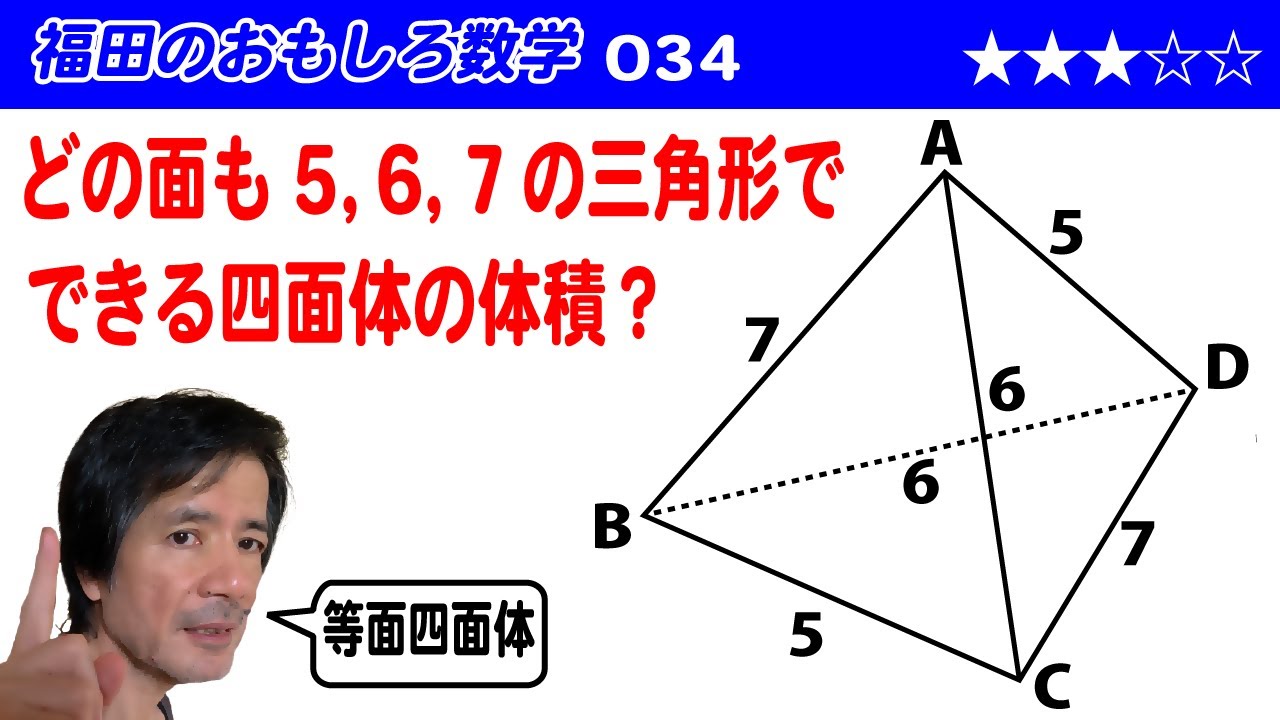
どの面も、5,6,7の長さの三角形でできている四面体の体積を求めよ
この動画を見る
どの面も、5,6,7の長さの三角形でできている四面体の体積を求めよ
六角形バリアは不可能じゃね?

単元:
#図形の性質#空間における垂直と平行と多面体(オイラーの法則)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
葬送のフリーレンのバリアなどで六角形で球を作っている件に関して解説していきます。
この動画を見る
葬送のフリーレンのバリアなどで六角形で球を作っている件に関して解説していきます。
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
福田の数学〜共通テスト対策にもってこい〜明治大学2023年全学部統一ⅠⅡAB第3問〜四面体の体積
単元:
#数A#大学入試過去問(数学)#図形の性質#センター試験・共通テスト関連#学校別大学入試過去問解説(数学)#共通テスト#空間における垂直と平行と多面体(オイラーの法則)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
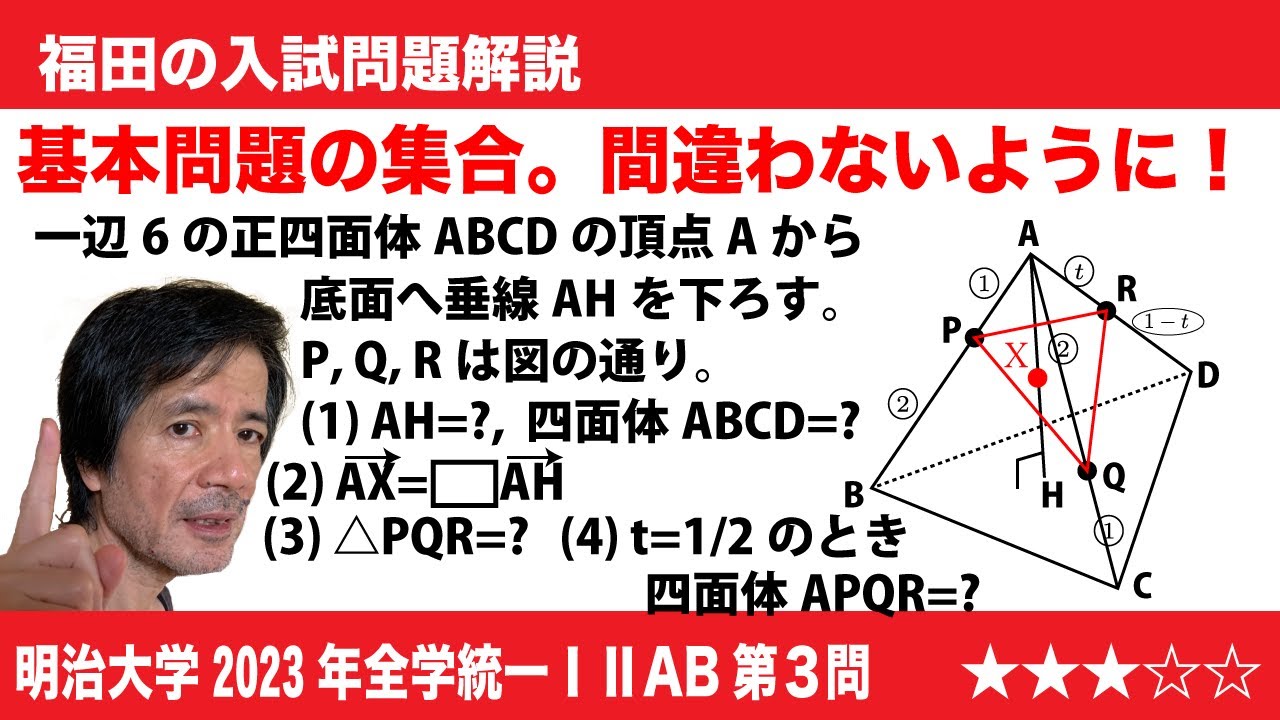
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
この動画を見る
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
福田の数学〜どれだけの情報を引き出せるかが勝負〜早稲田大学2023年商学部第2問〜球に内接する四面体の体積の最大

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 中心O、半径1の球に内接する四面体で、その4頂点$T_1$, $T_2$, $T_3$, $T_4$が次の条件(i), (ii)を満たすものを考える。
(i)|$\overrightarrow{T_1T_2}$|=$\sqrt 3$
(ii)$k$($\overrightarrow{OT_1}$+$\overrightarrow{OT_2}$)+$\overrightarrow{OT_3}$+$\overrightarrow{OT_4}$=$\overrightarrow{0}$
ここで、$k$は2未満の正の実数とする。次の設問に答えよ。
(1)線分$T_3T_4$の中点をMとしたとき、$\triangleT_1T_2M$の面積を$k$を用いて表せ。
(2)各$k$に対し、上の条件を満たす四面体の体積の最大値を$V(k)$とする。$V(k)$が最大になるときの$k$の値を求めよ。
この動画を見る
$\Large{\boxed{2}}$ 中心O、半径1の球に内接する四面体で、その4頂点$T_1$, $T_2$, $T_3$, $T_4$が次の条件(i), (ii)を満たすものを考える。
(i)|$\overrightarrow{T_1T_2}$|=$\sqrt 3$
(ii)$k$($\overrightarrow{OT_1}$+$\overrightarrow{OT_2}$)+$\overrightarrow{OT_3}$+$\overrightarrow{OT_4}$=$\overrightarrow{0}$
ここで、$k$は2未満の正の実数とする。次の設問に答えよ。
(1)線分$T_3T_4$の中点をMとしたとき、$\triangleT_1T_2M$の面積を$k$を用いて表せ。
(2)各$k$に対し、上の条件を満たす四面体の体積の最大値を$V(k)$とする。$V(k)$が最大になるときの$k$の値を求めよ。
福田の数学〜上智大学2023年理工学部第1問(3)〜正四面体を切った断面

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)一辺の長さが2である正四面体OABCにおいて、辺OAの中点をM、辺BCの中点をNとする。
(i)線分MNの長さは$\boxed{\ \ あ\ \ }$である。
(ii)0<$s$<1とし、線分MNを$s$:$(1-s)$に内分する点をPとする。Pを通りMNに垂直な平面で四面体OABCを切った断面は$\boxed{\ \ い\ \ }$であり、その面積は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }$の選択肢
(a)1 (b)$\sqrt 2$ (c)$\sqrt 3$ (d)2 (e)$\frac{1+\sqrt 5}{2}$ (f)$\frac{\sqrt 6}{2}$
$\boxed{\ \ い\ \ }$の選択肢
(a)正三角形 (b)正三角形でない二等辺三角形 (c)二等辺三角形でない三角形 (d)長方形 (e)長方形でない平行四辺形 (f)平行四辺形でない四角形
$\boxed{\ \ う\ \ }$の選択肢
(a)$s^2$ (b)$(1-s)^2$ (c)$s(1-s)$ (d)$s\sqrt{1-s^2}$
(e)$2s^2$ (f)$2(1-s)^2$ (g)$2s(1-s)$ (h)$2s\sqrt{1-s^2}$
(i)$4s^2$ (j)$4(1-s)^2$ (k)$4s(1-s)$ (l)$4s\sqrt{1-s^2}$
この動画を見る
$\Large{\boxed{1}}$ (3)一辺の長さが2である正四面体OABCにおいて、辺OAの中点をM、辺BCの中点をNとする。
(i)線分MNの長さは$\boxed{\ \ あ\ \ }$である。
(ii)0<$s$<1とし、線分MNを$s$:$(1-s)$に内分する点をPとする。Pを通りMNに垂直な平面で四面体OABCを切った断面は$\boxed{\ \ い\ \ }$であり、その面積は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }$の選択肢
(a)1 (b)$\sqrt 2$ (c)$\sqrt 3$ (d)2 (e)$\frac{1+\sqrt 5}{2}$ (f)$\frac{\sqrt 6}{2}$
$\boxed{\ \ い\ \ }$の選択肢
(a)正三角形 (b)正三角形でない二等辺三角形 (c)二等辺三角形でない三角形 (d)長方形 (e)長方形でない平行四辺形 (f)平行四辺形でない四角形
$\boxed{\ \ う\ \ }$の選択肢
(a)$s^2$ (b)$(1-s)^2$ (c)$s(1-s)$ (d)$s\sqrt{1-s^2}$
(e)$2s^2$ (f)$2(1-s)^2$ (g)$2s(1-s)$ (h)$2s\sqrt{1-s^2}$
(i)$4s^2$ (j)$4(1-s)^2$ (k)$4s(1-s)$ (l)$4s\sqrt{1-s^2}$
福田の数学〜上智大学2023年TEAP利用型文系第2問〜空間ベクトルと正八面体

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 図のような一辺の長さが1の正八面体ABCDEFがある。
2点P,Qはそれぞれ辺AD, BC上にあり
$\overrightarrow{PQ}$$\bot$$\overrightarrow{AD}$かつ$\overrightarrow{PQ}$$\bot$$\overrightarrow{BC}$
を満たすとする。
(1)$\overrightarrow{AD}$と$\overrightarrow{BC}$のなす角は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$である。
(2)|$\overrightarrow{AP}$|=$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$, |$\overrightarrow{BQ}$|=$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$である。
(3)|$\overrightarrow{PQ}$|=$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\sqrt{\boxed{\ \ ナ\ \ }}$である。
(4)平面EPQと直線BFの交点をRとすると|$\overrightarrow{BR}$|=$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$である。
この動画を見る
$\Large\boxed{2}$ 図のような一辺の長さが1の正八面体ABCDEFがある。
2点P,Qはそれぞれ辺AD, BC上にあり
$\overrightarrow{PQ}$$\bot$$\overrightarrow{AD}$かつ$\overrightarrow{PQ}$$\bot$$\overrightarrow{BC}$
を満たすとする。
(1)$\overrightarrow{AD}$と$\overrightarrow{BC}$のなす角は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$である。
(2)|$\overrightarrow{AP}$|=$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$, |$\overrightarrow{BQ}$|=$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$である。
(3)|$\overrightarrow{PQ}$|=$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\sqrt{\boxed{\ \ ナ\ \ }}$である。
(4)平面EPQと直線BFの交点をRとすると|$\overrightarrow{BR}$|=$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$である。
ほぼ使わない正二十面体の書き方

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#その他#数学(高校生)#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
正二十面体の書き方動画です
この動画を見る
正二十面体の書き方動画です
福田の数学〜筑波大学2023年理系第3問〜球面に内接する四面体

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標空間内の原点Oを中心とする半径$r$の球面S上に4つの頂点がある四面体ABCDが
$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=$\overrightarrow{0}$
を満たしているとする。また三角形ABCの重心をGとする。
(1)$\overrightarrow{OG}$を$\overrightarrow{OD}$を用いて表せ。
(2)$\overrightarrow{OA}$・$\overrightarrow{OB}$+$\overrightarrow{OB}$・$\overrightarrow{OC}$+$\overrightarrow{OC}$・$\overrightarrow{OA}$を$r$を用いて表せ。
(3)点Pが球面S上を動くとき、$\overrightarrow{PA}$・$\overrightarrow{PB}$+$\overrightarrow{PB}$・$\overrightarrow{PC}$+$\overrightarrow{PC}$・$\overrightarrow{PA}$の最大値を$r$を用いて表せ。さらに、最大値をとるときの点Pに対して、|$\overrightarrow{PG}$|を$r$を用いて表せ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{3}$ 座標空間内の原点Oを中心とする半径$r$の球面S上に4つの頂点がある四面体ABCDが
$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=$\overrightarrow{0}$
を満たしているとする。また三角形ABCの重心をGとする。
(1)$\overrightarrow{OG}$を$\overrightarrow{OD}$を用いて表せ。
(2)$\overrightarrow{OA}$・$\overrightarrow{OB}$+$\overrightarrow{OB}$・$\overrightarrow{OC}$+$\overrightarrow{OC}$・$\overrightarrow{OA}$を$r$を用いて表せ。
(3)点Pが球面S上を動くとき、$\overrightarrow{PA}$・$\overrightarrow{PB}$+$\overrightarrow{PB}$・$\overrightarrow{PC}$+$\overrightarrow{PC}$・$\overrightarrow{PA}$の最大値を$r$を用いて表せ。さらに、最大値をとるときの点Pに対して、|$\overrightarrow{PG}$|を$r$を用いて表せ。
2023筑波大学理系過去問
福田の数学〜神戸大学2023年理系第4問〜平面に下ろした垂線ベクトルと四面体の体積
単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#神戸大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
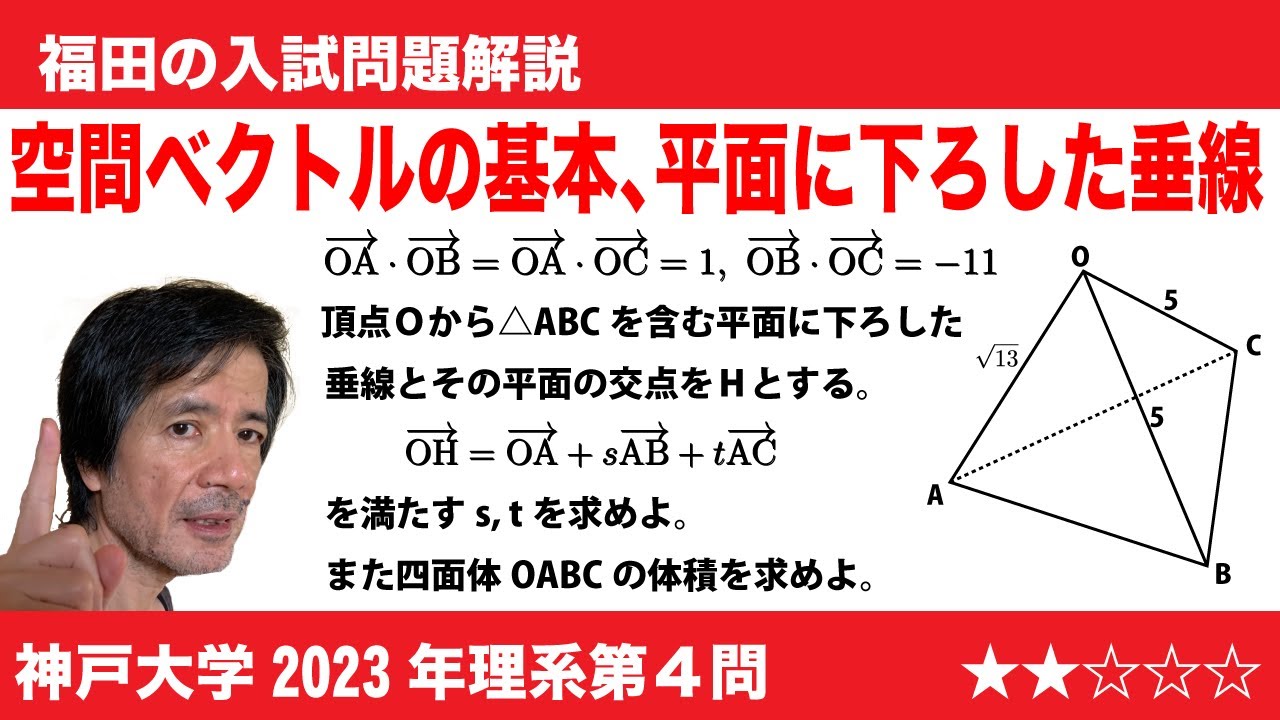
$\Large\boxed{4}$ 四面体OABCがあり、辺OA, OB, OCの長さはそれぞれ$\sqrt{13}$, 5, 5である。
$\overrightarrow{OA}$・$\overrightarrow{OB}$=$\overrightarrow{OA}$・$\overrightarrow{OC}$=1, $\overrightarrow{OB}$・$\overrightarrow{OC}$=-11 とする。頂点Oから$\triangle$ABCを含む平面に下ろした垂線とその平面の交点をHとする。以下の問いに答えよ。
(1)線分ABの長さを求めよ。
(2)実数$s$, $t$を$\overrightarrow{OH}$=$\overrightarrow{OA}$+$s\overrightarrow{AB}$+$t\overrightarrow{AC}$ を満たすように定めるとき、$s$と$t$の値を求めよ。
(3)四面体OABCの体積を求めよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{4}$ 四面体OABCがあり、辺OA, OB, OCの長さはそれぞれ$\sqrt{13}$, 5, 5である。
$\overrightarrow{OA}$・$\overrightarrow{OB}$=$\overrightarrow{OA}$・$\overrightarrow{OC}$=1, $\overrightarrow{OB}$・$\overrightarrow{OC}$=-11 とする。頂点Oから$\triangle$ABCを含む平面に下ろした垂線とその平面の交点をHとする。以下の問いに答えよ。
(1)線分ABの長さを求めよ。
(2)実数$s$, $t$を$\overrightarrow{OH}$=$\overrightarrow{OA}$+$s\overrightarrow{AB}$+$t\overrightarrow{AC}$ を満たすように定めるとき、$s$と$t$の値を求めよ。
(3)四面体OABCの体積を求めよ。
2023神戸大学理系過去問
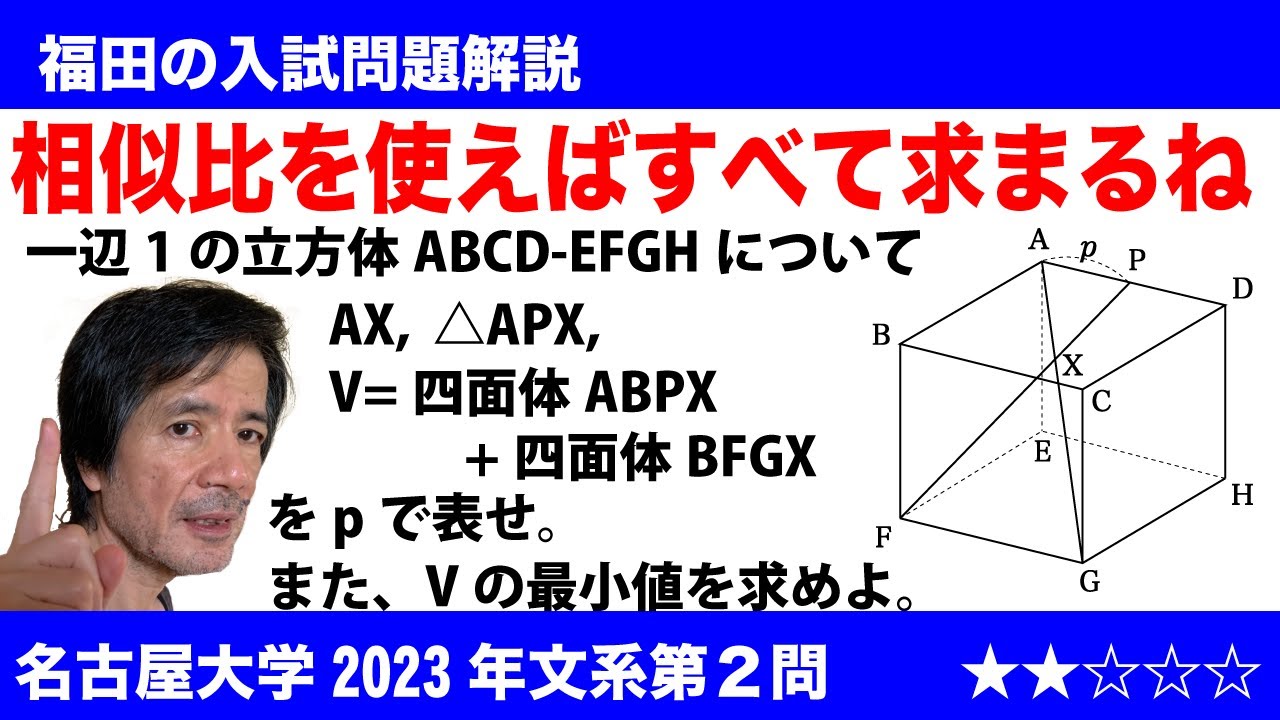
福田の数学〜名古屋大学2023年文系第2問〜空間図形と体積の最小
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#式と証明#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 図のような1辺の長さが1の立方体ABCD-EFGHにおいて、辺AD上に点Pをとり、線分APの長さをpとする。このとき、線分AGと線分FPは四角形ADGF上で交わる。その交点をXとする。(※図は動画参照)
(1)線分AXの長さをpを用いて表せ。
(2)三角形APXの面積をpを用いて表せ。
(3)四面体ABPXと四面体EFGXの体積の和をVとする。
Vをpを用いて表せ。
(4)点Pを辺AD上で動かすとき、Vの最小値を求めよ。
2023名古屋大学文系過去問
この動画を見る
$\Large\boxed{2}$ 図のような1辺の長さが1の立方体ABCD-EFGHにおいて、辺AD上に点Pをとり、線分APの長さをpとする。このとき、線分AGと線分FPは四角形ADGF上で交わる。その交点をXとする。(※図は動画参照)
(1)線分AXの長さをpを用いて表せ。
(2)三角形APXの面積をpを用いて表せ。
(3)四面体ABPXと四面体EFGXの体積の和をVとする。
Vをpを用いて表せ。
(4)点Pを辺AD上で動かすとき、Vの最小値を求めよ。
2023名古屋大学文系過去問
【数A】【難問】正二十面体の体積を求めよ。

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
教材:
#チャート式#青チャートⅠ・A#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1辺の長さが1の正二十面体の体積を求めなさい。
この動画を見る
1辺の長さが1の正二十面体の体積を求めなさい。
福田の数学〜東京大学2023年理系第6問〜線分の先端の可動範囲と関節を加えたときの可動範囲(PART1)

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ Oを原点とする座標空間において、不等式|x|≦1, |y|≦1, |z|≦1の表す立方体を考える。その立方体の表面のうち、z<1を満たす部分をSとする。
以下、座標空間内の2点A,Bが一致するとき、線分ABは点Aを表すものとし、その長さを0と定める。
(1)座標空間内の点Pが次の条件(i),(ii)をともに満たすとき、点Pが動きうる範囲Vの体積を求めよ。
(i)OP≦$\sqrt 3$
(ii)線分OPとSは、共有点をもたないか、点Pのみを共有点にもつ。
(2)座標空間内の点Nと点Pが次の条件(iii),(iv),(v)をすべて満たすとき、点Pが動きうる範囲Wの体積を求めよ。必要ならば、$\sin\alpha$=$\frac{1}{\sqrt 3}$を満たす実数α(0<α<$\frac{\pi}{2}$)を用いてよい。
(iii)ON+NP≦$\sqrt 3$
(iv)線分ONとSは共有点を持たない。
(v)線分NPとSは、共有点を持たないか、点Pのみを共有点を持つ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{6}$ Oを原点とする座標空間において、不等式|x|≦1, |y|≦1, |z|≦1の表す立方体を考える。その立方体の表面のうち、z<1を満たす部分をSとする。
以下、座標空間内の2点A,Bが一致するとき、線分ABは点Aを表すものとし、その長さを0と定める。
(1)座標空間内の点Pが次の条件(i),(ii)をともに満たすとき、点Pが動きうる範囲Vの体積を求めよ。
(i)OP≦$\sqrt 3$
(ii)線分OPとSは、共有点をもたないか、点Pのみを共有点にもつ。
(2)座標空間内の点Nと点Pが次の条件(iii),(iv),(v)をすべて満たすとき、点Pが動きうる範囲Wの体積を求めよ。必要ならば、$\sin\alpha$=$\frac{1}{\sqrt 3}$を満たす実数α(0<α<$\frac{\pi}{2}$)を用いてよい。
(iii)ON+NP≦$\sqrt 3$
(iv)線分ONとSは共有点を持たない。
(v)線分NPとSは、共有点を持たないか、点Pのみを共有点を持つ。
2023東京大学理系過去問
【数学】オイラーの定理の公式 笑っちゃう覚え方

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
オイラーの定理の公式 笑っちゃう覚え方に関して解説していきます.
この動画を見る
オイラーの定理の公式 笑っちゃう覚え方に関して解説していきます.
福田の数学〜早稲田大学2022年商学部第3問〜空間図形の計量

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
この動画を見る
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
福田の数学〜早稲田大学2022年理工学部第4問〜正八面体の内部に配置した6個の球の和集合の体積と共通部分の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$一辺の長さが$\sqrt3+1$である正八面体の頂点を右図(※動画参照)
のように$P_1,P_2,P_3,P_4,P_5,P_6$とする。$i=1,2,\ldots,6$に対して
$P_i$以外の5点を頂点とする四角錐のすべての面に
内接する球(内部含む)を$B_i$とする。$B_1$の体積をXとし、$B_1$と
$B_2$の共通部分の体積をYとし、$B_1,B_2,B_3$の共通部分の体積をZ
とする。さらに$B_1,B_2,\ldots,B_n$を合わせて得られる立体の体積を
$V_n\ \ (n=2,3,\ldots,6)$とする。以下の問いに答えよ。
(1)$V_n=aX+bY+cZ$となる整数a,b,cを$n=2,3,6$の場合
について求めよ。
(2)Xの値を求めよ。
(3)$V_2$の値を求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{4}}$一辺の長さが$\sqrt3+1$である正八面体の頂点を右図(※動画参照)
のように$P_1,P_2,P_3,P_4,P_5,P_6$とする。$i=1,2,\ldots,6$に対して
$P_i$以外の5点を頂点とする四角錐のすべての面に
内接する球(内部含む)を$B_i$とする。$B_1$の体積をXとし、$B_1$と
$B_2$の共通部分の体積をYとし、$B_1,B_2,B_3$の共通部分の体積をZ
とする。さらに$B_1,B_2,\ldots,B_n$を合わせて得られる立体の体積を
$V_n\ \ (n=2,3,\ldots,6)$とする。以下の問いに答えよ。
(1)$V_n=aX+bY+cZ$となる整数a,b,cを$n=2,3,6$の場合
について求めよ。
(2)Xの値を求めよ。
(3)$V_2$の値を求めよ。
2022早稲田大学理工学部過去問
福田の数学・入試問題解説〜東北大学2022年文系第4問〜空間における四面体の高さと体積

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
xyz空間内の点O(0,0,0),$A(1,\sqrt2,\sqrt3),B(-\sqrt3,0,1),C(\sqrt6,-\sqrt3,\sqrt2)$
を頂点とする四面体OABCを考える。3点OABを含む平面からの距離が1の点
のうち、点Oに最も近く、x座標が正のものをHとする。
(1)Hの座標を求めよ。
(2)3点OABを含む平面と点Cの距離を求めよ。
(3)四面体OABCの体積を求めよ。
2022東北大学文系過去問
この動画を見る
xyz空間内の点O(0,0,0),$A(1,\sqrt2,\sqrt3),B(-\sqrt3,0,1),C(\sqrt6,-\sqrt3,\sqrt2)$
を頂点とする四面体OABCを考える。3点OABを含む平面からの距離が1の点
のうち、点Oに最も近く、x座標が正のものをHとする。
(1)Hの座標を求めよ。
(2)3点OABを含む平面と点Cの距離を求めよ。
(3)四面体OABCの体積を求めよ。
2022東北大学文系過去問
福田の数学〜慶應義塾大学2022年薬学部第1問(7)〜直三角柱の切断面の面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形の性質#微分法と積分法#学校別大学入試過去問解説(数学)#立体図形#立体切断#空間における垂直と平行と多面体(オイラーの法則)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(7)1辺の長さが$\sqrt2$の正三角形を底面とし、高さが4の直三角柱を考える。
この直三角柱を以下の条件①と条件②を共に満たす平面で切断するとき、切断面の
面積の最小値は$\boxed{\ \ シ\ \ }$である。ただし、直三角柱は底面と側面が垂直である三角柱
のことである。
条件① 切断面が直角三角形になる。
条件② 切断面の図形のすべての辺が直三角柱の側面上にある。
2022慶應義塾大学薬学部過去問
この動画を見る
(7)1辺の長さが$\sqrt2$の正三角形を底面とし、高さが4の直三角柱を考える。
この直三角柱を以下の条件①と条件②を共に満たす平面で切断するとき、切断面の
面積の最小値は$\boxed{\ \ シ\ \ }$である。ただし、直三角柱は底面と側面が垂直である三角柱
のことである。
条件① 切断面が直角三角形になる。
条件② 切断面の図形のすべての辺が直三角柱の側面上にある。
2022慶應義塾大学薬学部過去問
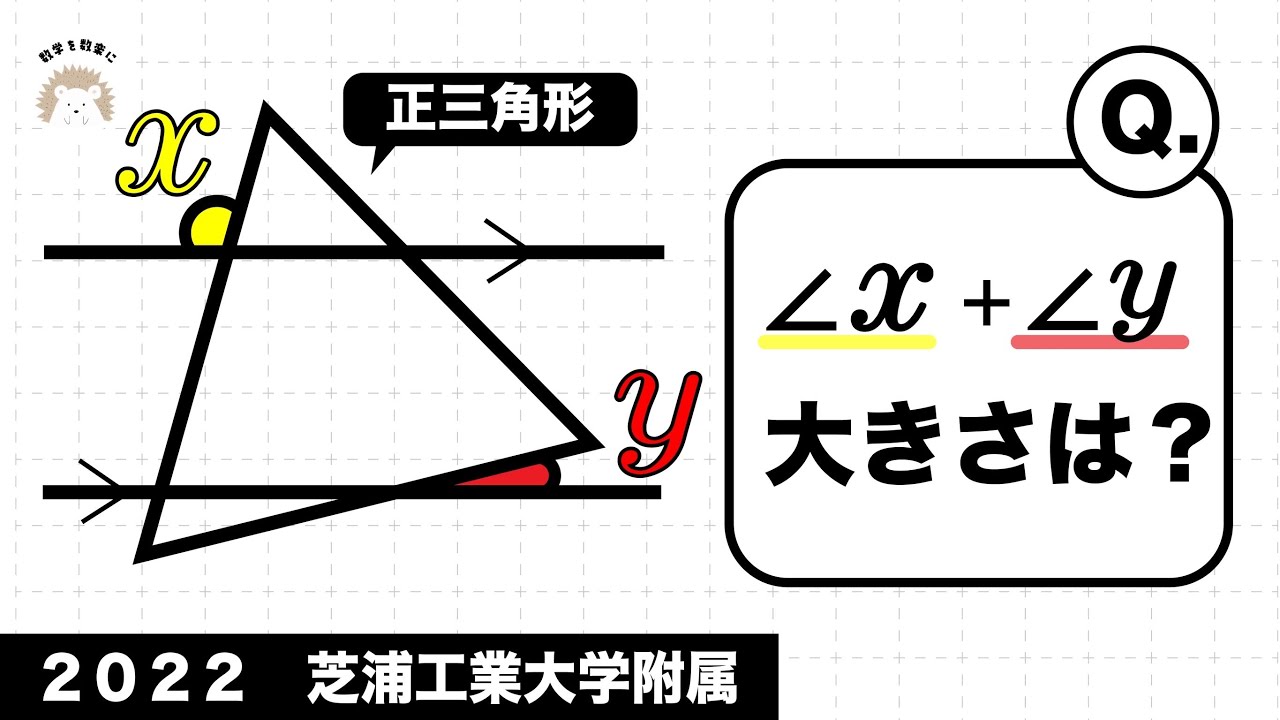
平行線と角の和 芝浦工大附属 2022年入試問題解説46問目
単元:
#数学(中学生)#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x+ \angle y$=?
*図は動画内参照
2022芝浦工業大学附属高等学校
この動画を見る
$\angle x+ \angle y$=?
*図は動画内参照
2022芝浦工業大学附属高等学校
空間上の3本の直線

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
空間内の3本の直線l,m,nに対して、l⊥m、かつl⊥nならば、
常にm$/\!/$n
この動画を見る
空間内の3本の直線l,m,nに対して、l⊥m、かつl⊥nならば、
常にm$/\!/$n
福田の数学〜慶應義塾大学2021年薬学部第1問(7)〜四面体の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (7)座標空間内に4点$A(0,-2,2),\ B(0,2,2),\ C(2,0,-2),\ D(-2,0,-2)$がある。
この4点を頂点とする四面体ABCDの体積は$\boxed{シ}$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{1}}$ (7)座標空間内に4点$A(0,-2,2),\ B(0,2,2),\ C(2,0,-2),\ D(-2,0,-2)$がある。
この4点を頂点とする四面体ABCDの体積は$\boxed{シ}$である。
2021慶應義塾大学薬学部過去問
名古屋大学文学部卒のゆる言語学者にオイラーの公式は理解できるのか?

福田の数学〜早稲田大学2021年商学部第2問〜空間図形の共通部分

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
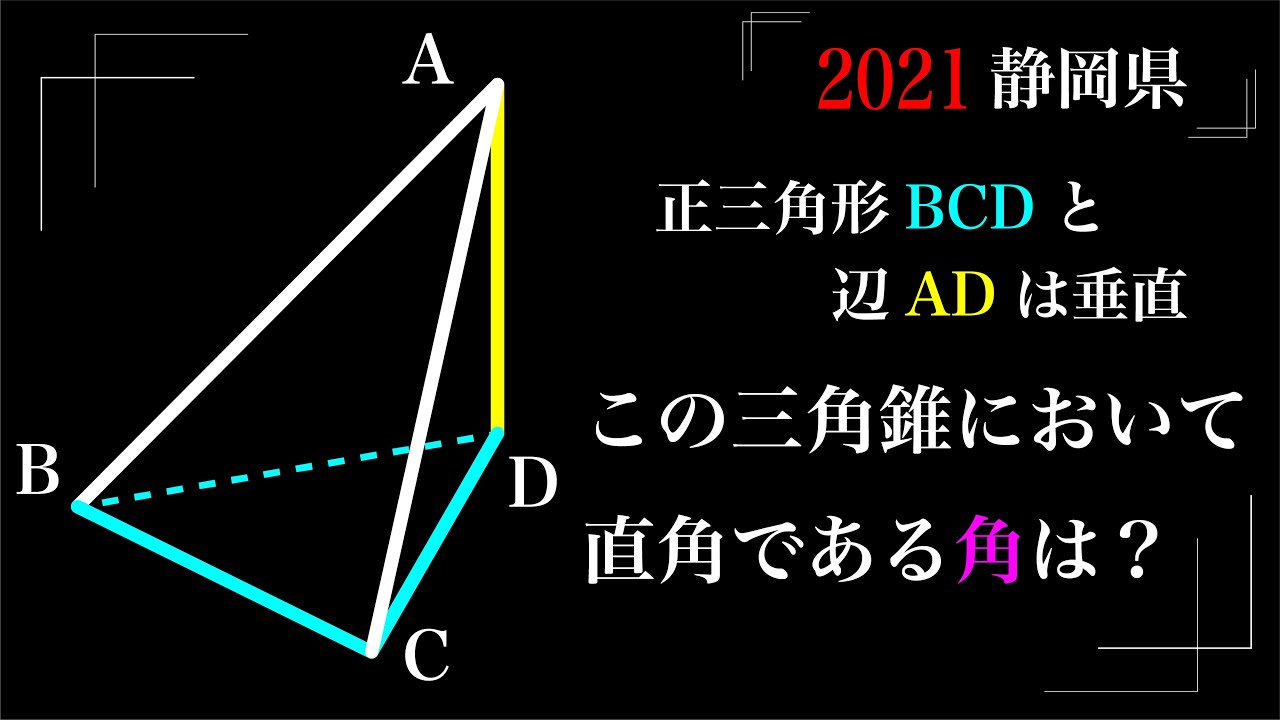
空間図形 垂直について 簡単だけど大切です。
単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$AD⊥△BCD$
直角である角は?
*図は動画内参照
2021静岡県
この動画を見る
$AD⊥△BCD$
直角である角は?
*図は動画内参照
2021静岡県
正十二角形の中の三角形の個数

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正十二角形の3つの頂点を結んでできる三角形の個数は$\boxed{ア}$コである。
そのうち
・2辺を共有する三角形は$\boxed{イ}$コ
・1辺を共有する三角形は$\boxed{ウ}$コ
・辺を共有しない三角形は$\boxed{エ}$コ
・直角三角形は$\boxed{オ}$コ
・正三角形は$\boxed{カ}$コ
・二等辺三角形は$\boxed{キ}$コ
ある。
*図は動画内参照
この動画を見る
正十二角形の3つの頂点を結んでできる三角形の個数は$\boxed{ア}$コである。
そのうち
・2辺を共有する三角形は$\boxed{イ}$コ
・1辺を共有する三角形は$\boxed{ウ}$コ
・辺を共有しない三角形は$\boxed{エ}$コ
・直角三角形は$\boxed{オ}$コ
・正三角形は$\boxed{カ}$コ
・二等辺三角形は$\boxed{キ}$コ
ある。
*図は動画内参照
四面体の体積(垂線はどこに落ちる??)慶應義塾 2021 C

単元:
#数学(中学生)#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
体積=?
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
体積=?
*図は動画内参照
2021慶應義塾高等学校
