 図形の性質
図形の性質
 図形の性質
図形の性質
福田の数学〜明治大学2022年全学部統一入試12AB第3問〜漸化式の図形への応用

単元:
#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数列#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
この動画を見る
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
座標平面上の直角三角形 立教新座
単元:
#数学(中学生)#中3数学#数A#図形の性質#2次関数#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
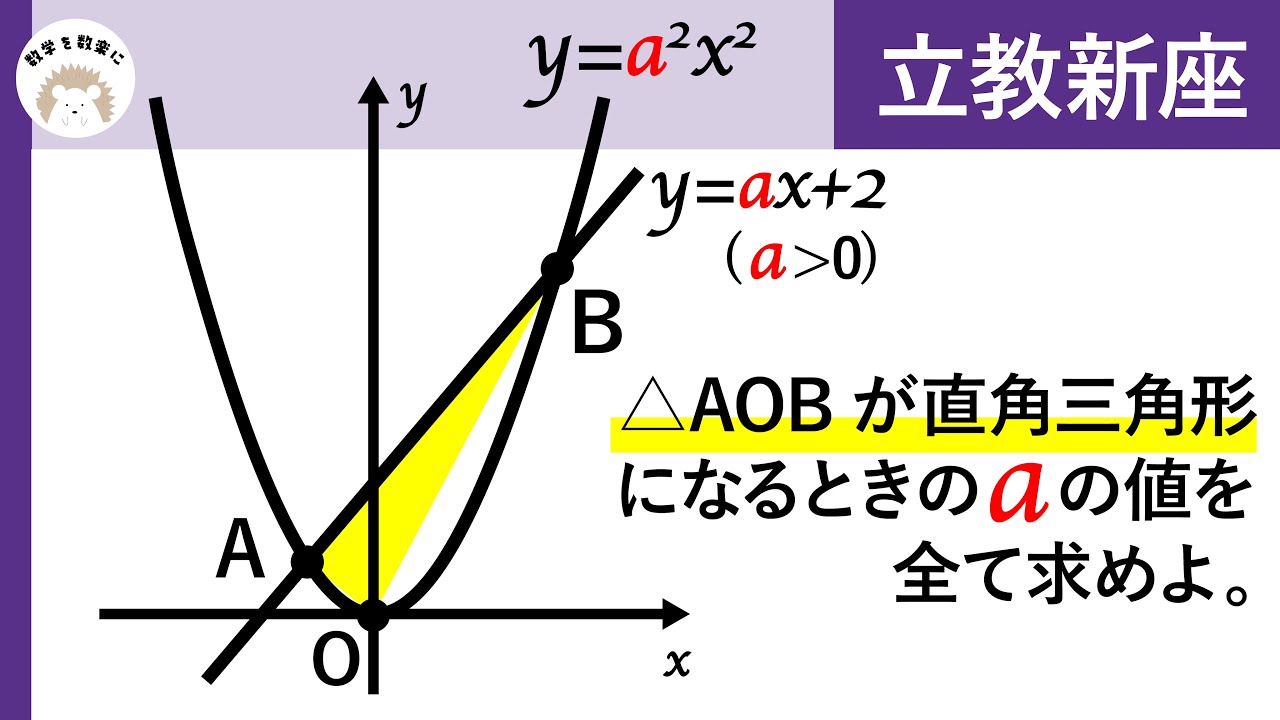
△AOBが直角三角形になるときのaの値を全て求めよ。
*図は動画内参照
立教新座高等学校
この動画を見る
△AOBが直角三角形になるときのaの値を全て求めよ。
*図は動画内参照
立教新座高等学校
角の三等分
福田の数学〜明治大学2022年全学部統一入試12AB第1問(4)〜角の二等分線と辺の長さの軽量

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
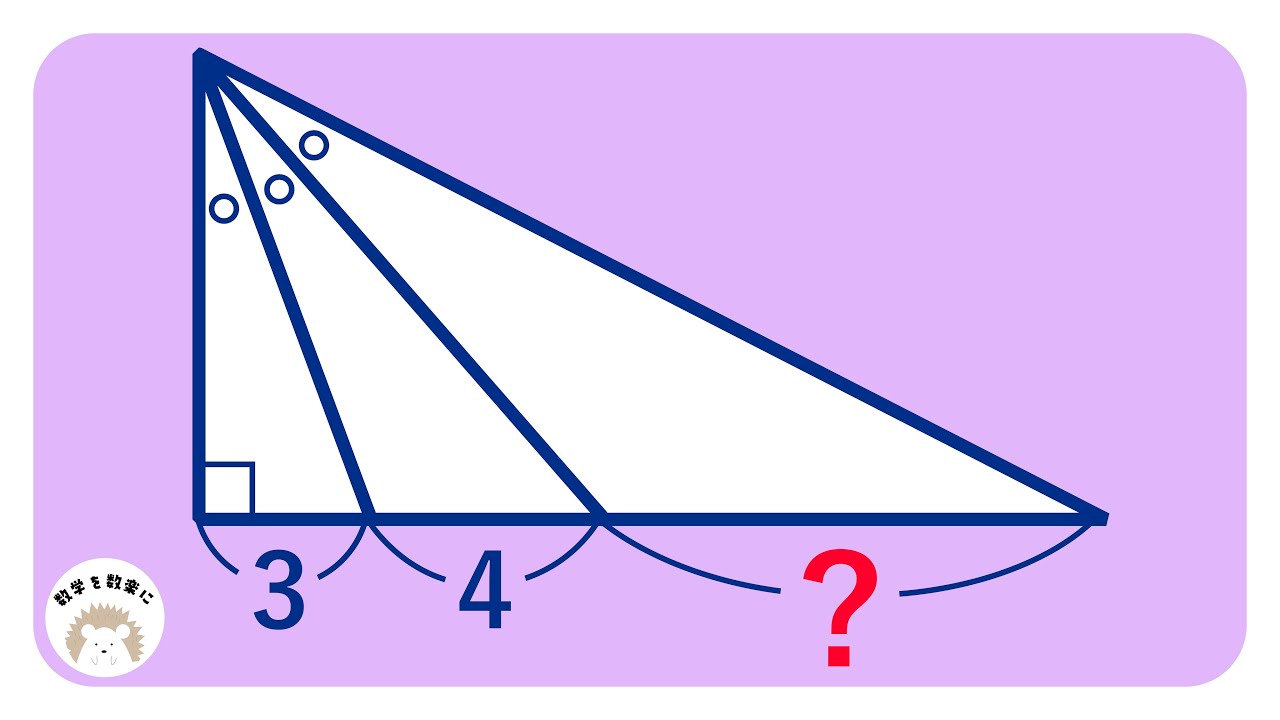
(4)三角形$ABC$の$\angle A$の二等分線と辺$BC$との交点をDとする。
$AB=8,\ AC=3,\ AD=4$とするとき、
$BD:CD=\boxed{\ \ ソ\ \ }:\boxed{\ \ タ\ \ }$であり、
$BC=\frac{\boxed{\ \ チツ\ \ }\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
2022明治大学全統過去問
この動画を見る
(4)三角形$ABC$の$\angle A$の二等分線と辺$BC$との交点をDとする。
$AB=8,\ AC=3,\ AD=4$とするとき、
$BD:CD=\boxed{\ \ ソ\ \ }:\boxed{\ \ タ\ \ }$であり、
$BC=\frac{\boxed{\ \ チツ\ \ }\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
2022明治大学全統過去問
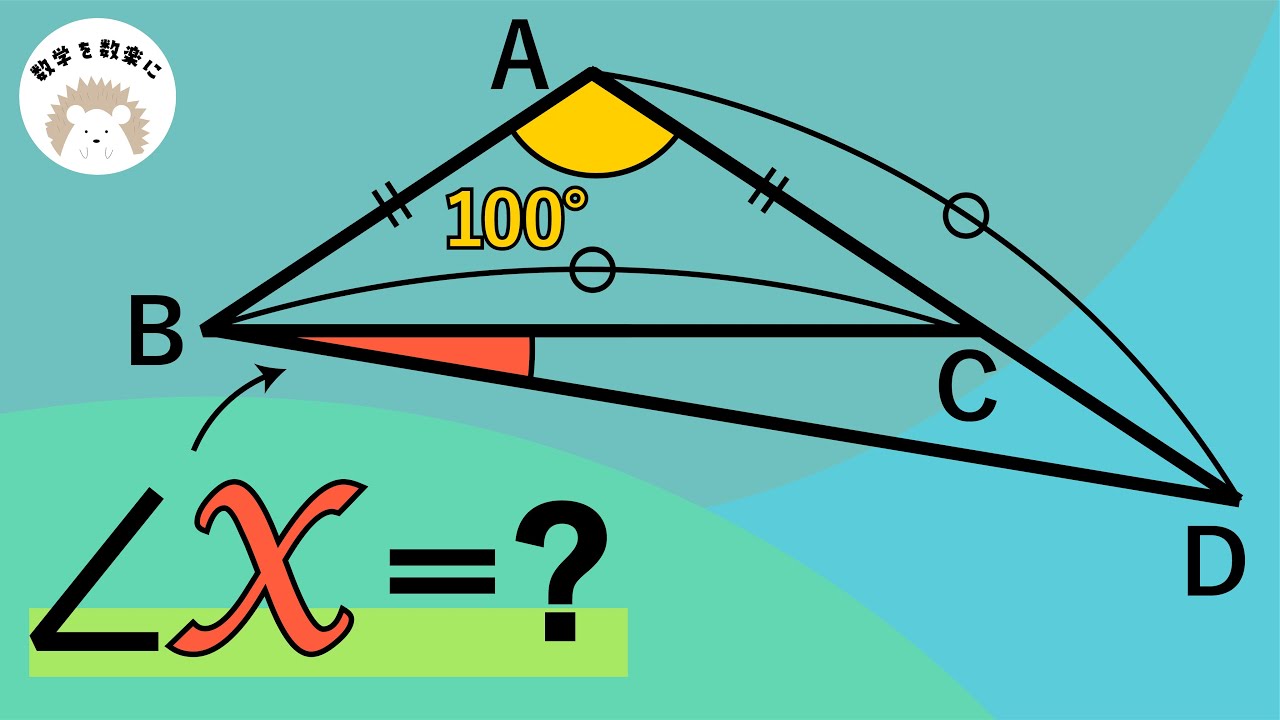
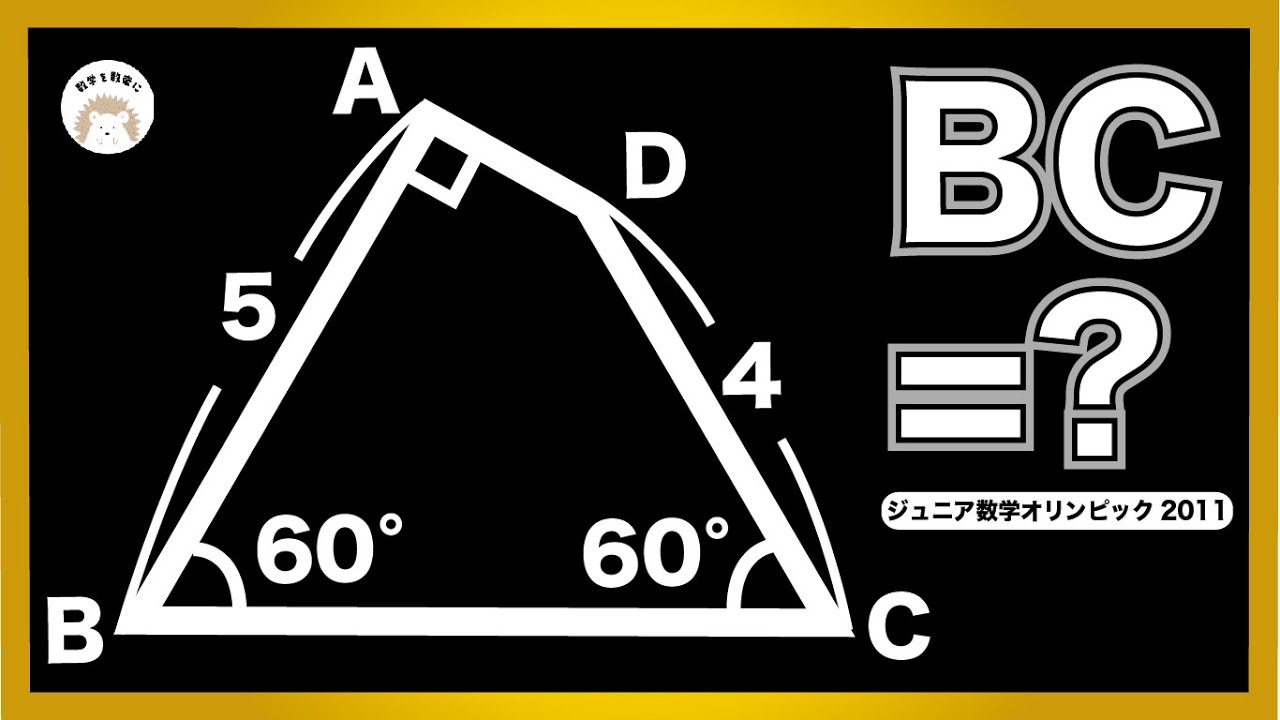
手強いよ。角度を求める問題。
見える人には〇〇が見える
仙台育英 正四面体の内接球の半径

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
内接球の半径=?
*図は動画内参照
仙台育英学園高等学校
この動画を見る
内接球の半径=?
*図は動画内参照
仙台育英学園高等学校
福田の数学〜早稲田大学2022年社会科学部第2問〜平面幾何と3次関数の増減

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
この動画を見る
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
福田の数学〜早稲田大学2022年商学部第3問〜空間図形の計量

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
この動画を見る
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
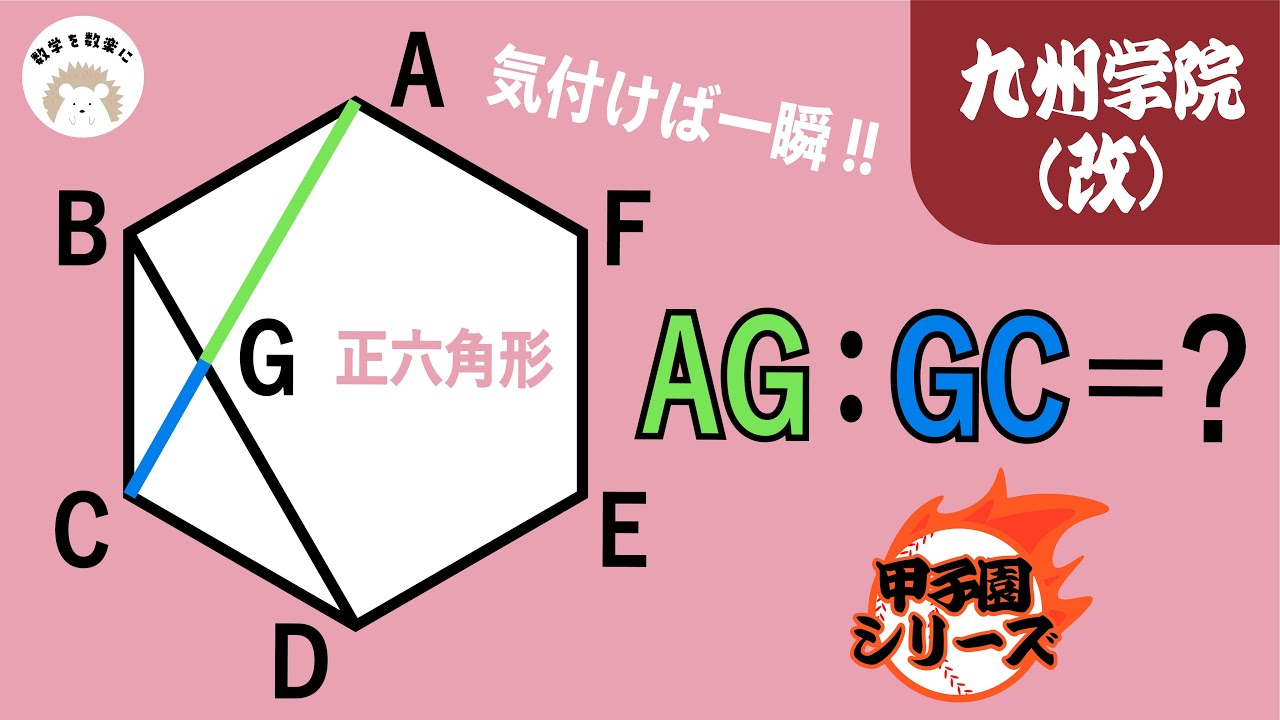
気付けば一瞬!! 正六角形 九州学院(熊本)
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AG:GC=?
*図は動画内参照
九州学院高等学校(改)
この動画を見る
AG:GC=?
*図は動画内参照
九州学院高等学校(改)
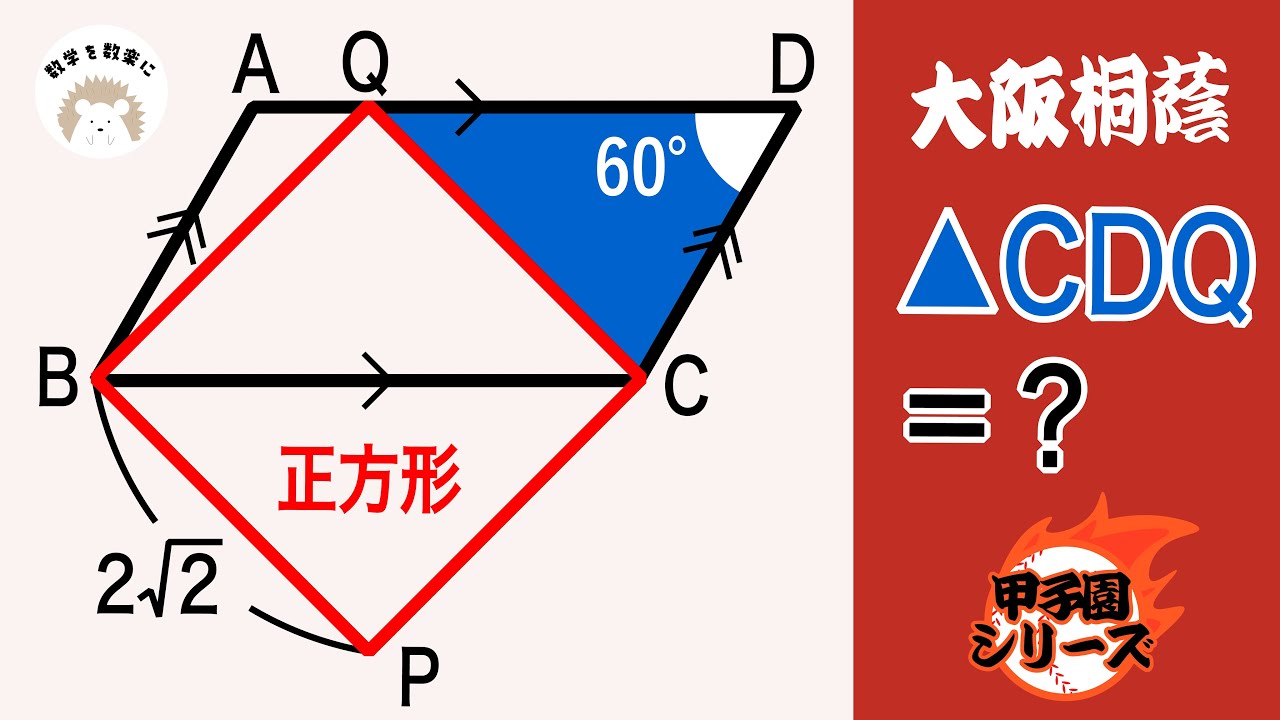
決め手は角度。大阪桐蔭
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△CDQ=?
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
△CDQ=?
*図は動画内参照
大阪桐蔭高等学校
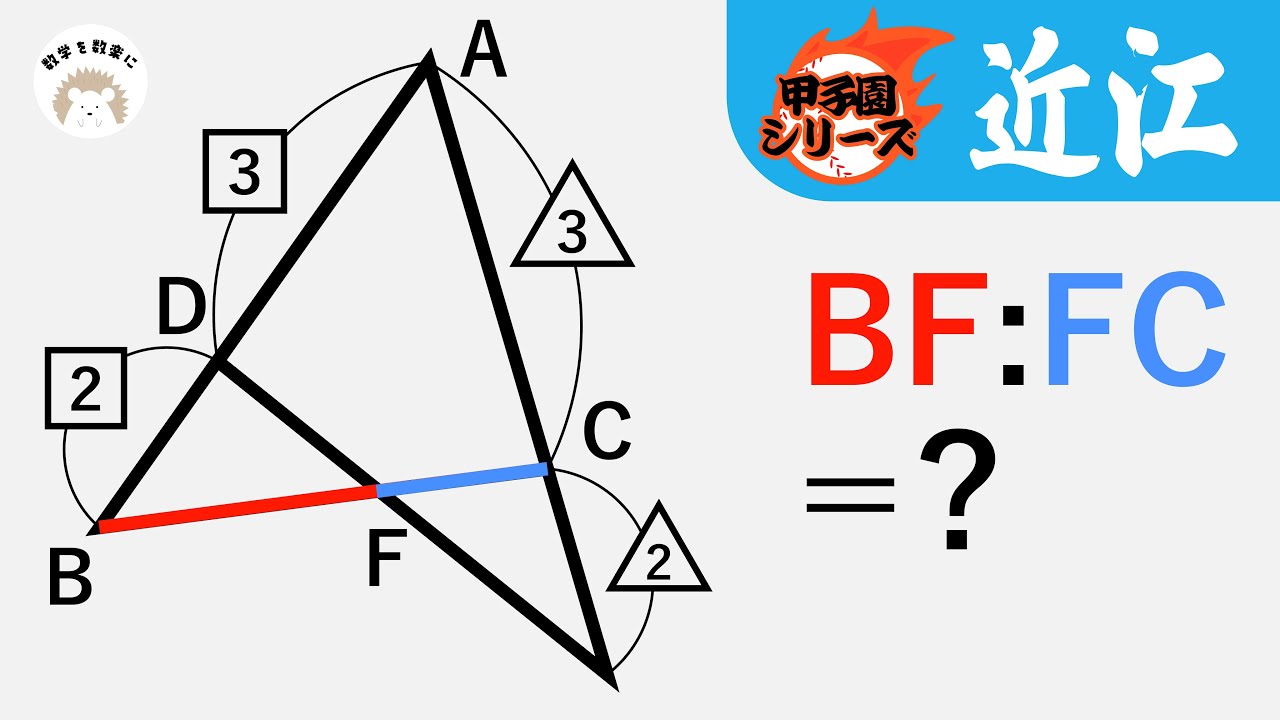
メネラウスの定理でも良いと思います。近江高校(滋賀)
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BF:FC=?
*図は動画内参照
近江高等学校
この動画を見る
BF:FC=?
*図は動画内参照
近江高等学校
図は正確とは限りません
福田の数学〜早稲田大学2022年理工学部第4問〜正八面体の内部に配置した6個の球の和集合の体積と共通部分の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$一辺の長さが$\sqrt3+1$である正八面体の頂点を右図(※動画参照)
のように$P_1,P_2,P_3,P_4,P_5,P_6$とする。$i=1,2,\ldots,6$に対して
$P_i$以外の5点を頂点とする四角錐のすべての面に
内接する球(内部含む)を$B_i$とする。$B_1$の体積をXとし、$B_1$と
$B_2$の共通部分の体積をYとし、$B_1,B_2,B_3$の共通部分の体積をZ
とする。さらに$B_1,B_2,\ldots,B_n$を合わせて得られる立体の体積を
$V_n\ \ (n=2,3,\ldots,6)$とする。以下の問いに答えよ。
(1)$V_n=aX+bY+cZ$となる整数a,b,cを$n=2,3,6$の場合
について求めよ。
(2)Xの値を求めよ。
(3)$V_2$の値を求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{4}}$一辺の長さが$\sqrt3+1$である正八面体の頂点を右図(※動画参照)
のように$P_1,P_2,P_3,P_4,P_5,P_6$とする。$i=1,2,\ldots,6$に対して
$P_i$以外の5点を頂点とする四角錐のすべての面に
内接する球(内部含む)を$B_i$とする。$B_1$の体積をXとし、$B_1$と
$B_2$の共通部分の体積をYとし、$B_1,B_2,B_3$の共通部分の体積をZ
とする。さらに$B_1,B_2,\ldots,B_n$を合わせて得られる立体の体積を
$V_n\ \ (n=2,3,\ldots,6)$とする。以下の問いに答えよ。
(1)$V_n=aX+bY+cZ$となる整数a,b,cを$n=2,3,6$の場合
について求めよ。
(2)Xの値を求めよ。
(3)$V_2$の値を求めよ。
2022早稲田大学理工学部過去問
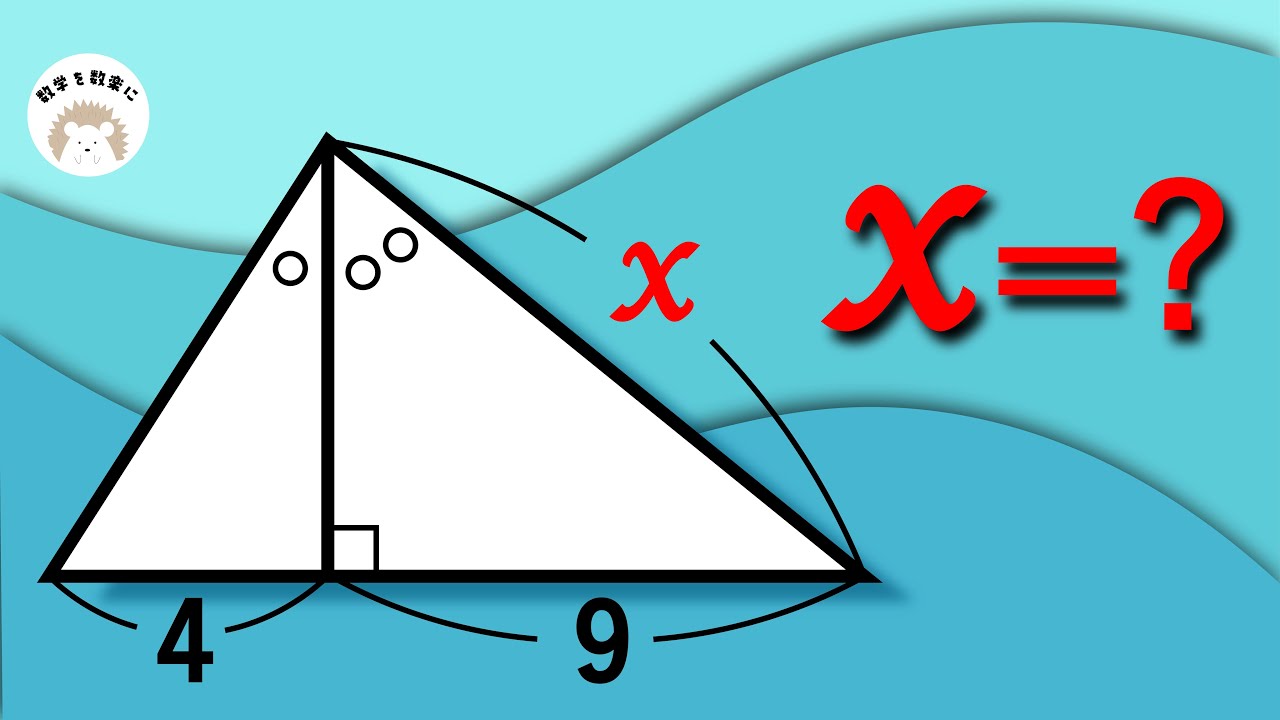
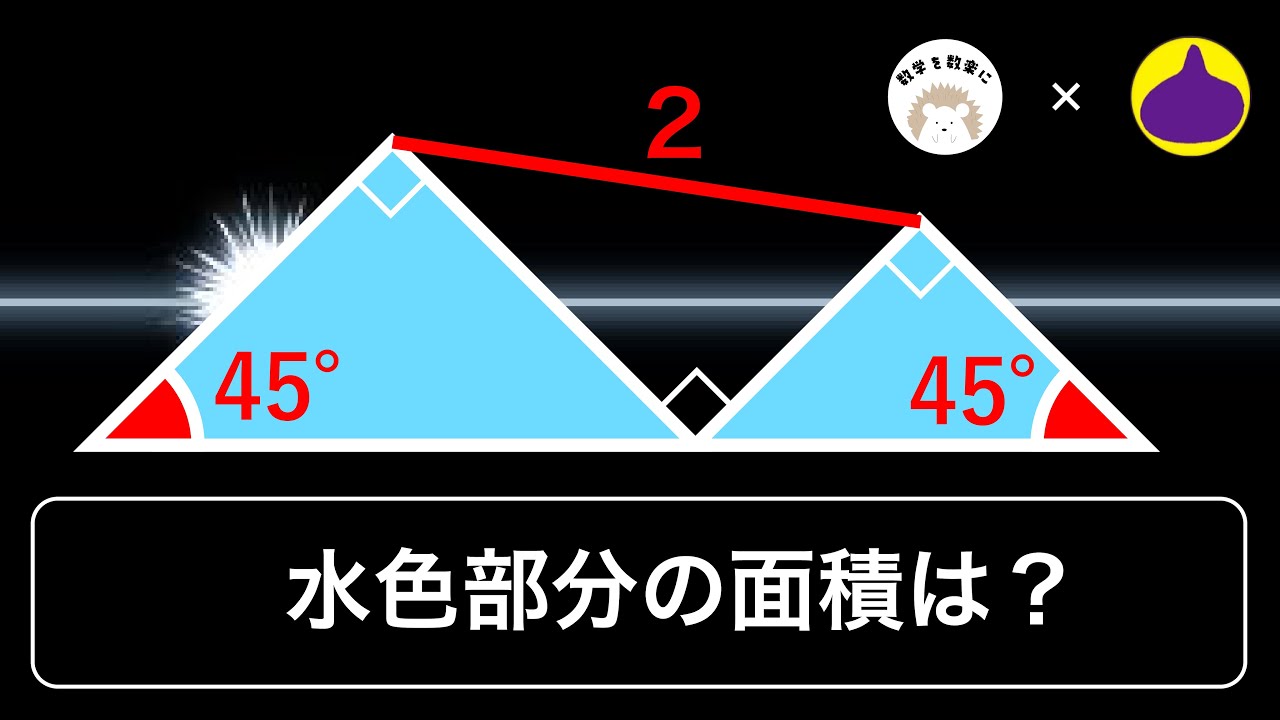
気付けば一瞬!!2つの直角二等辺三角形の面積の和
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2つの直角二等辺三角形の面積の和=?
*図は動画内参照
この動画を見る
2つの直角二等辺三角形の面積の和=?
*図は動画内参照
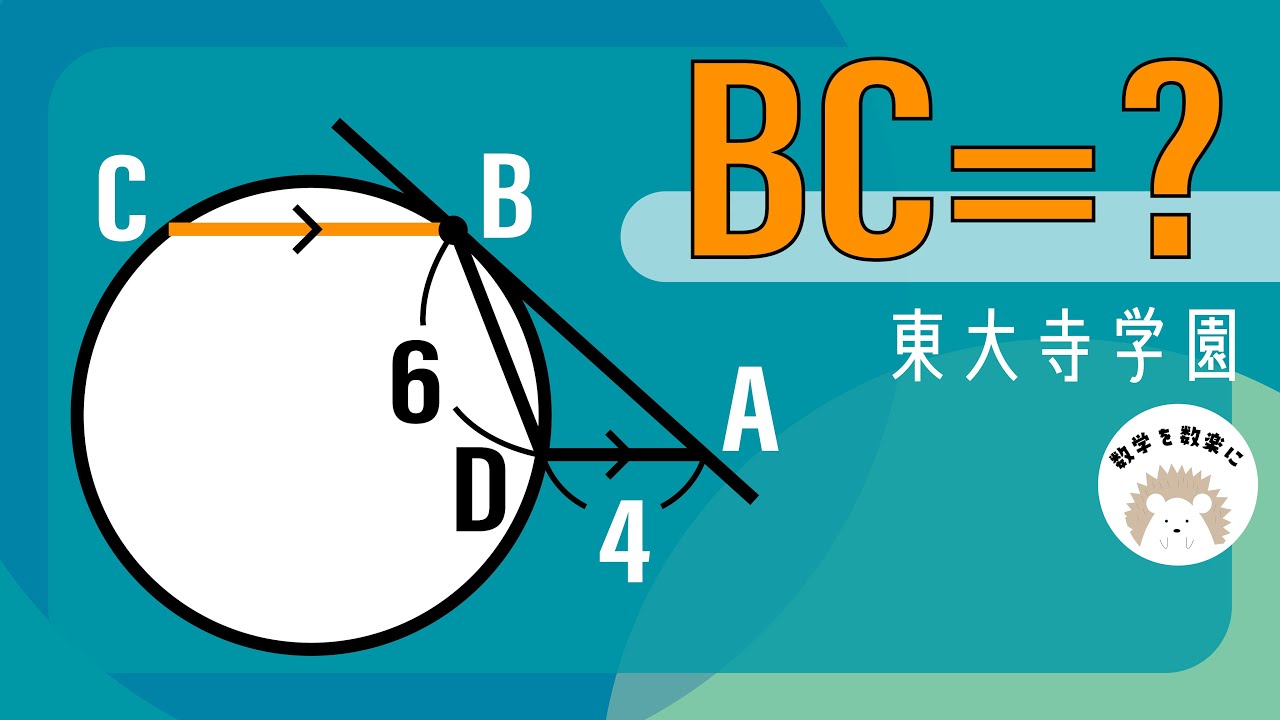
接線といったら〇〇定理
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BC=?
*図は動画内参照
東大寺学園高等学校
この動画を見る
BC=?
*図は動画内参照
東大寺学園高等学校
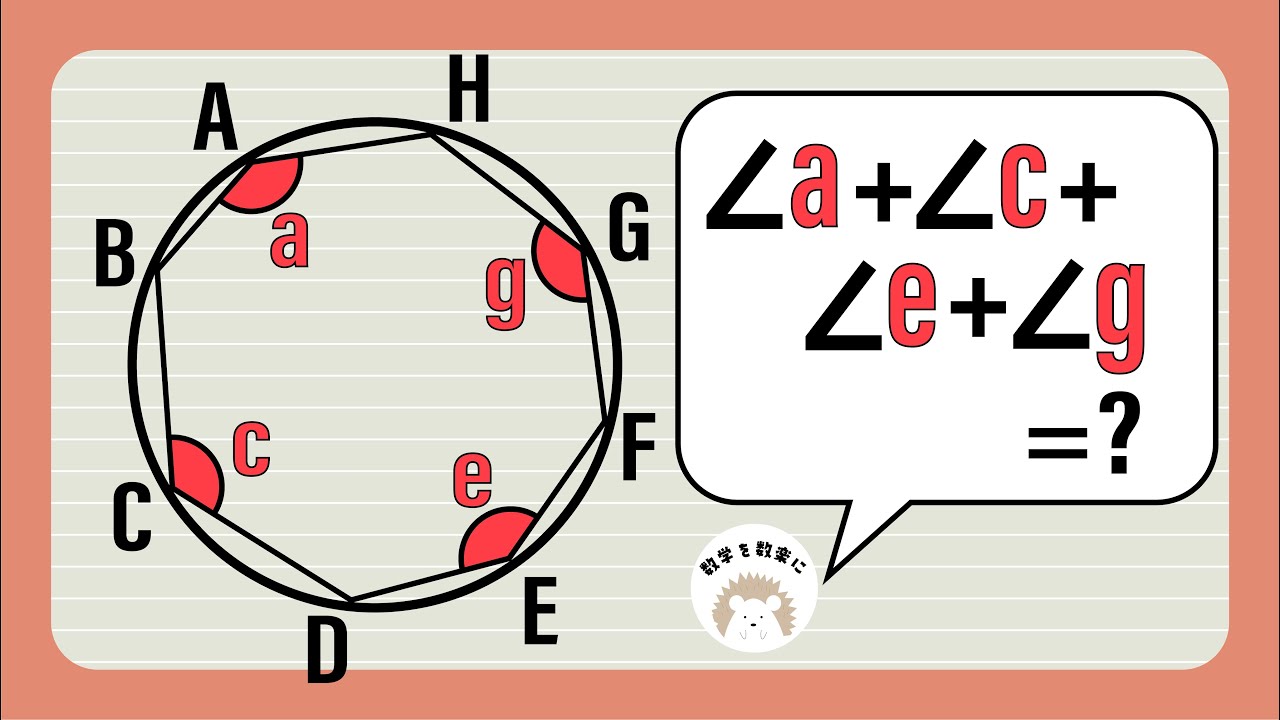
円と八角形と角の和
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a + \angle c + \angle e + \angle g = ?$
*図は動画内参照
この動画を見る
$\angle a + \angle c + \angle e + \angle g = ?$
*図は動画内参照
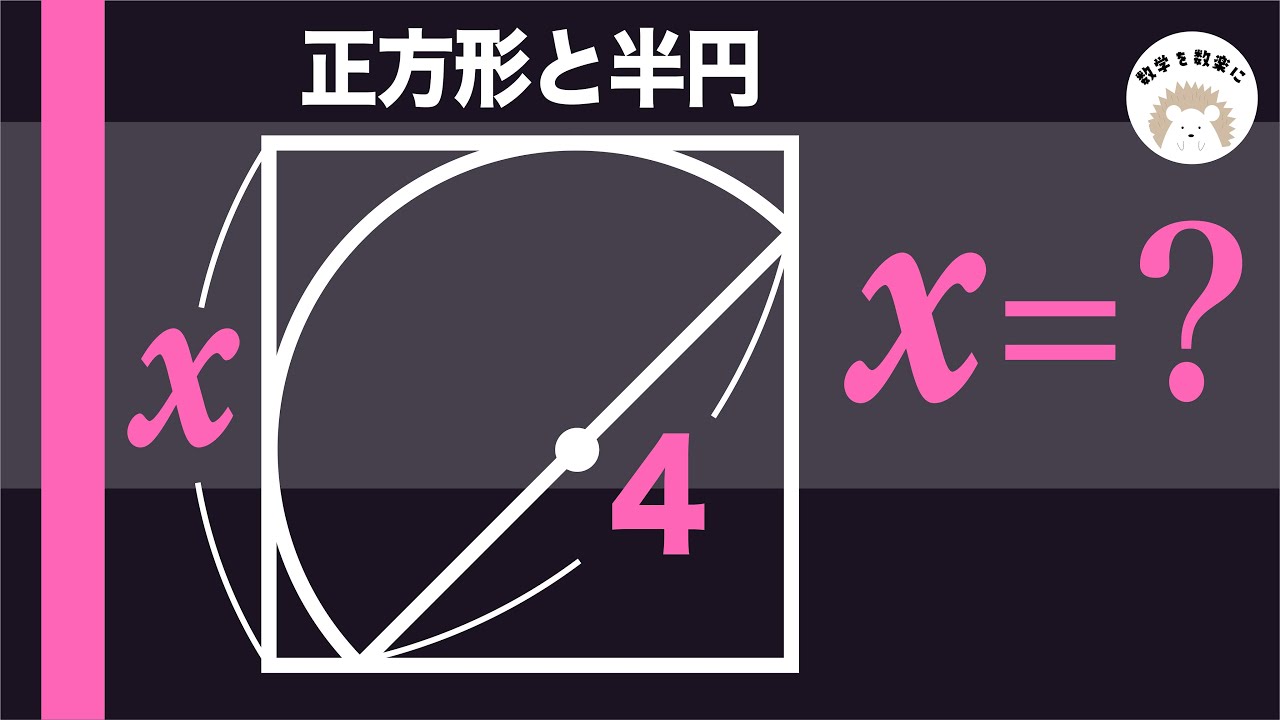
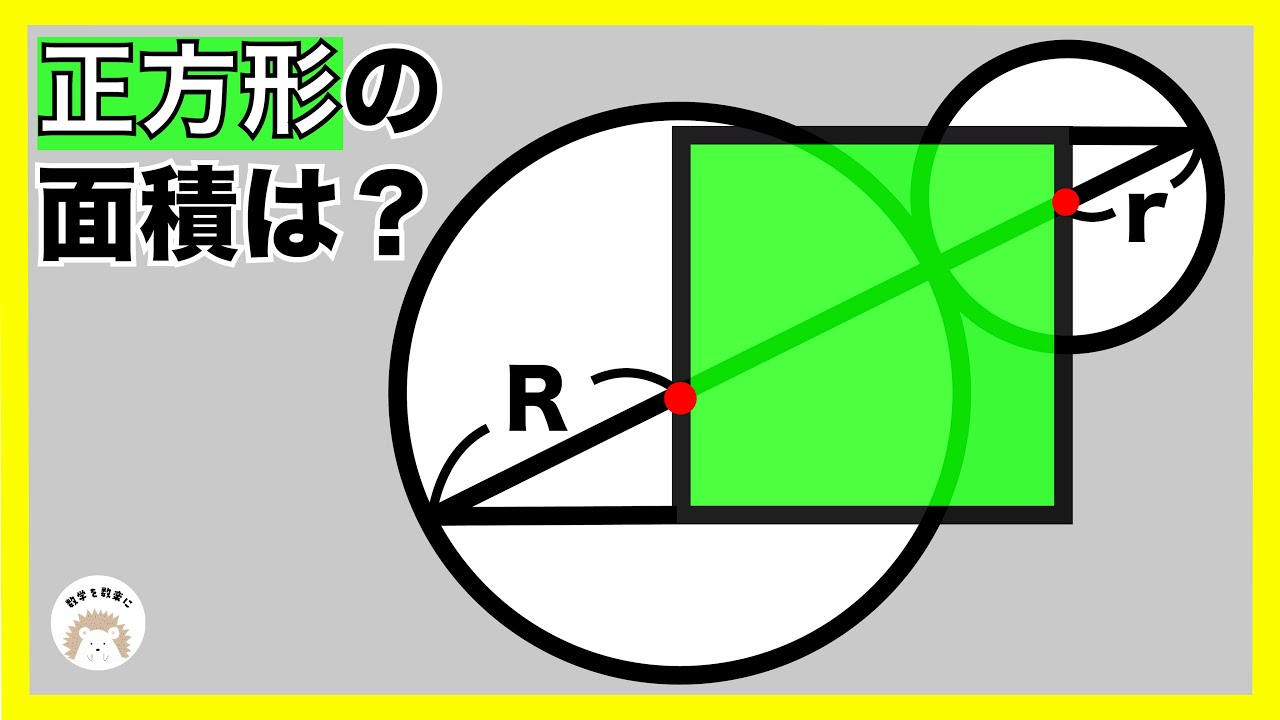
補助線引ける? 正方形と半円
ロニー先生再生リストあります
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正方形ABCDの面積をR、rで表せ。
*図は動画内参照
この動画を見る
正方形ABCDの面積をR、rで表せ。
*図は動画内参照
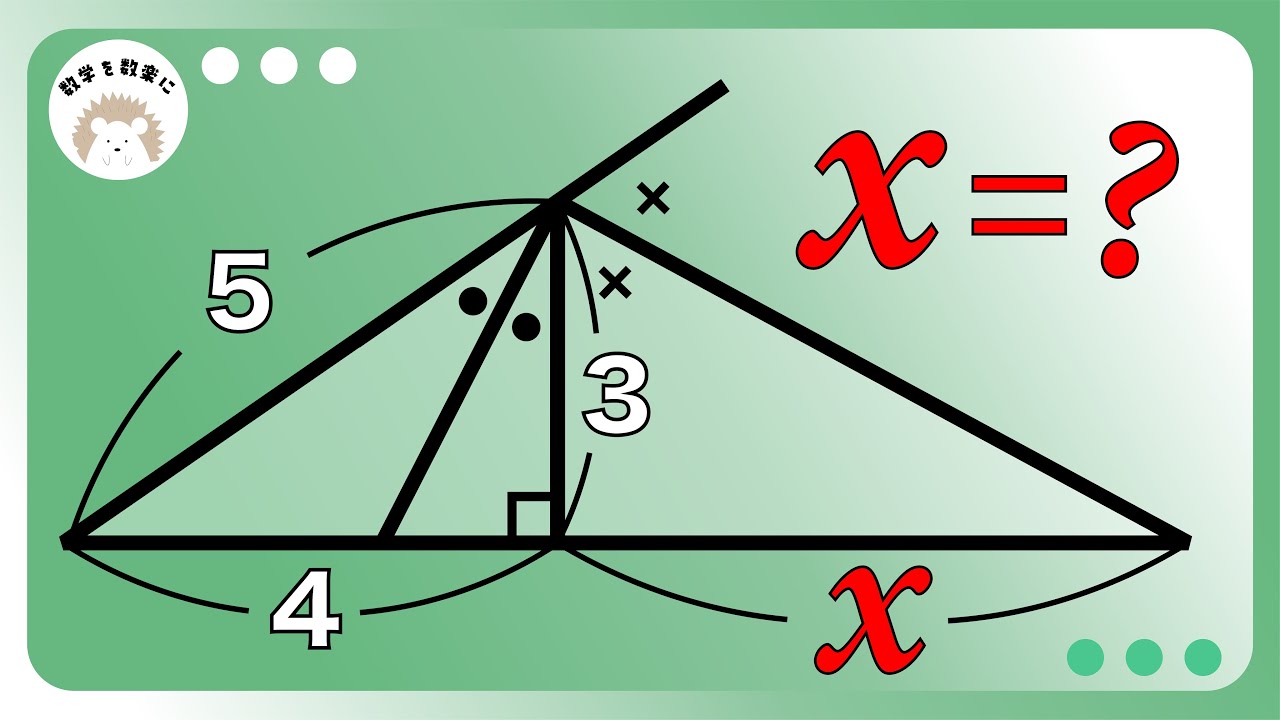
内角の二等分 外角の二等分
福田の数学〜慶應義塾大学2022年総合政策学部第5問〜等脚台形の外接円の中心の位置ベクトル

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}$いま、ADを下底、BCを上底とする台形ABCDにおいて、$\angle BAD=\angle CDA=60°,$
$|\overrightarrow{ AB }|=2,|\overrightarrow{ BC }|=1$となっている。
(1)$|\overrightarrow{ BD }|=\sqrt{\boxed{\ \ アイ\ \ }}$であり、台形ABCDの外接円の半径は$\frac{\sqrt{\boxed{\ \ ウエ\ \ }}}{\boxed{\ \ オカ\ \ }}$である。
(2)外接円の中心をOとするとき、内積$\overrightarrow{ AB }・\overrightarrow{ AO }=\boxed{\ \ キク\ \ },\overrightarrow{ AD }・\overrightarrow{ AO }=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(3)$\overrightarrow{ AO }=\frac{\boxed{\ \ スセ\ \ }}{\boxed{\ \ ソタ\ \ }}\ \overrightarrow{ AB }+\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \overrightarrow{ AD }$である。
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{5}}$いま、ADを下底、BCを上底とする台形ABCDにおいて、$\angle BAD=\angle CDA=60°,$
$|\overrightarrow{ AB }|=2,|\overrightarrow{ BC }|=1$となっている。
(1)$|\overrightarrow{ BD }|=\sqrt{\boxed{\ \ アイ\ \ }}$であり、台形ABCDの外接円の半径は$\frac{\sqrt{\boxed{\ \ ウエ\ \ }}}{\boxed{\ \ オカ\ \ }}$である。
(2)外接円の中心をOとするとき、内積$\overrightarrow{ AB }・\overrightarrow{ AO }=\boxed{\ \ キク\ \ },\overrightarrow{ AD }・\overrightarrow{ AO }=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(3)$\overrightarrow{ AO }=\frac{\boxed{\ \ スセ\ \ }}{\boxed{\ \ ソタ\ \ }}\ \overrightarrow{ AB }+\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \overrightarrow{ AD }$である。
2022慶應義塾大学総合政策学部過去問
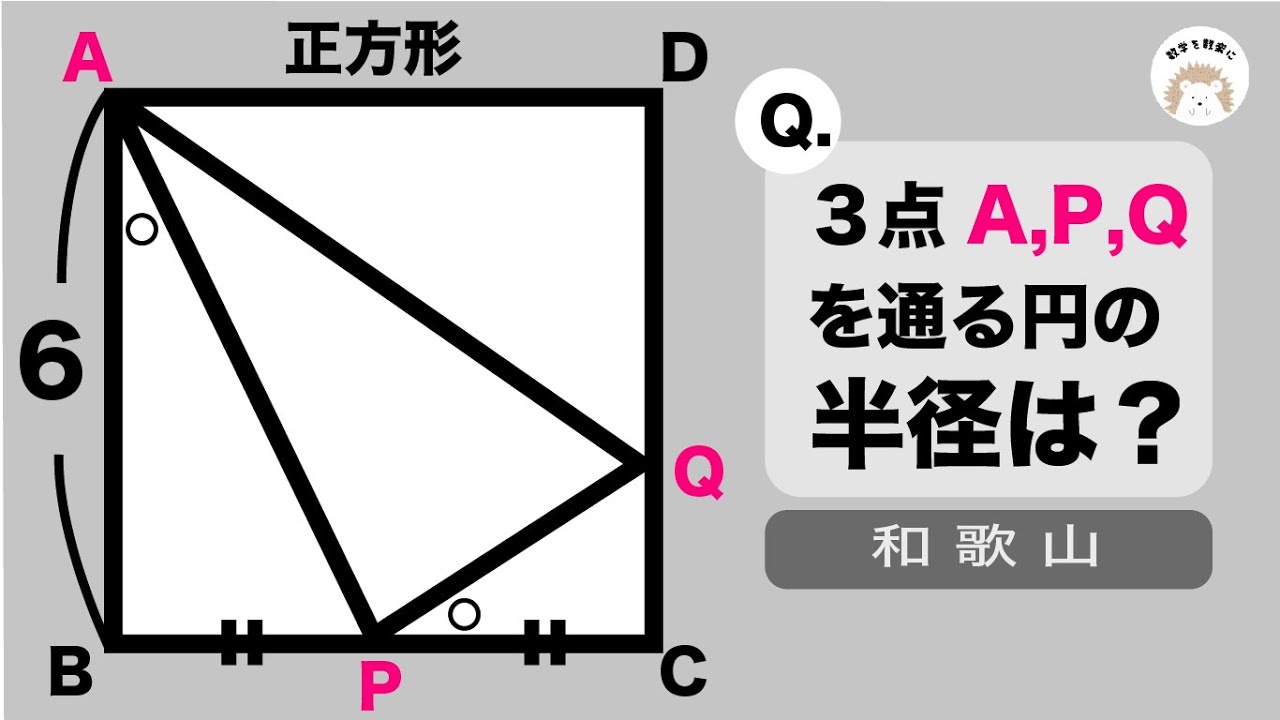
良問!!円の半径を求める 2022和歌山県ラスト問題
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
3点A,P,Qを通る円の半径は?
*図は動画内参照
2022和歌山県
この動画を見る
3点A,P,Qを通る円の半径は?
*図は動画内参照
2022和歌山県
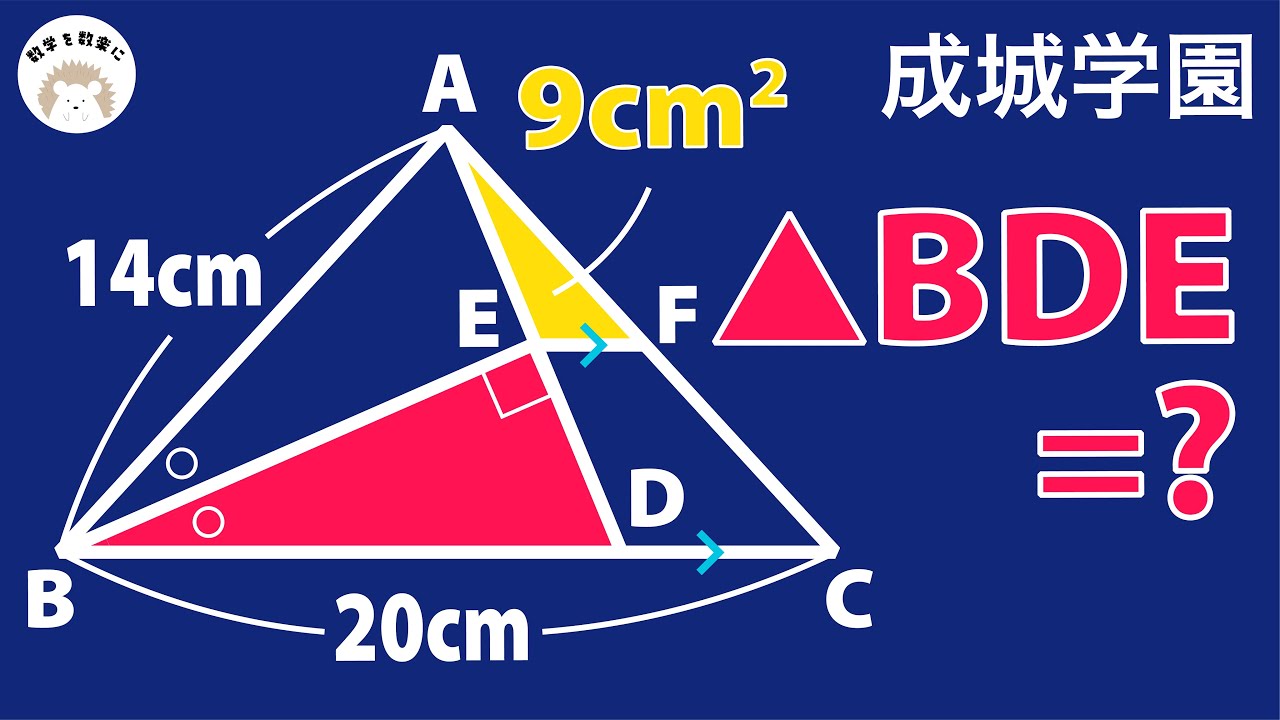
この一問で学べるものは多い。角の二等分 垂直 面積比 成城学園高校
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△AEF=9㎠
△BDE=?
*図は動画内参照
成城学園高等学校
この動画を見る
△AEF=9㎠
△BDE=?
*図は動画内参照
成城学園高等学校
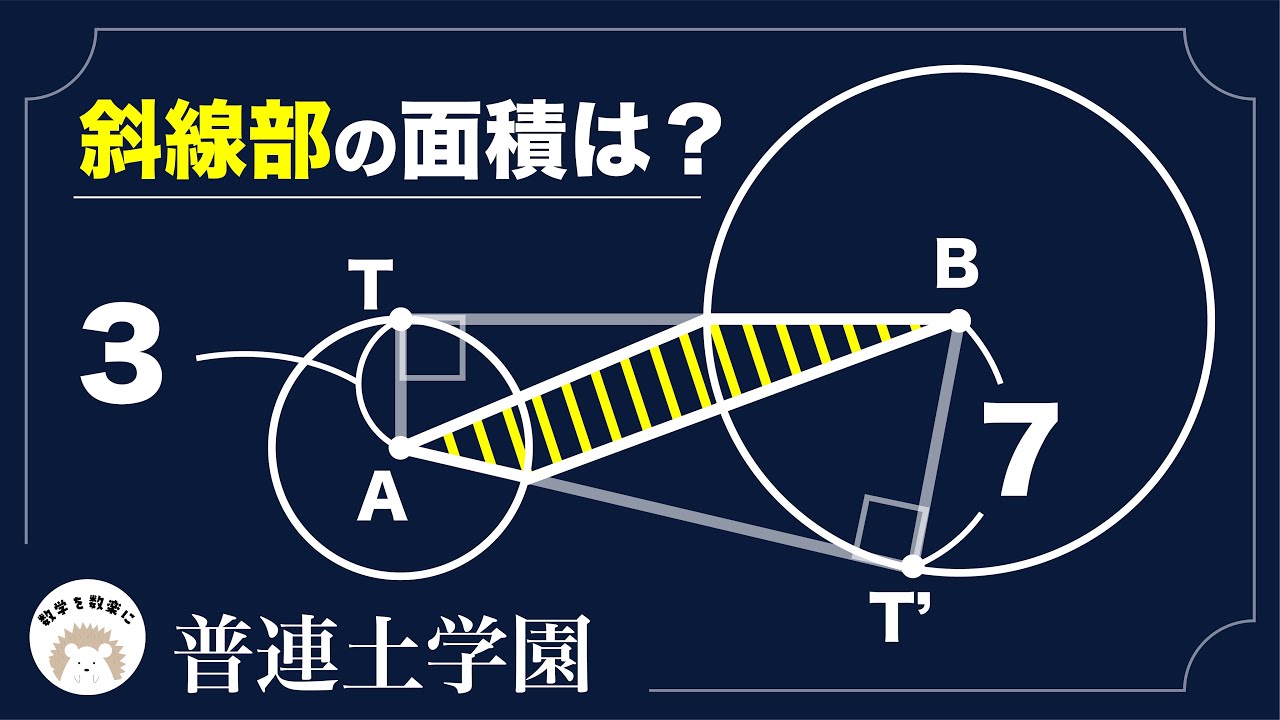
気付けば一瞬!!普連土学園
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積は?
*図は動画内参照
普連土学園高等学校
この動画を見る
斜線部の面積は?
*図は動画内参照
普連土学園高等学校
気が付けば一瞬!!面積の差
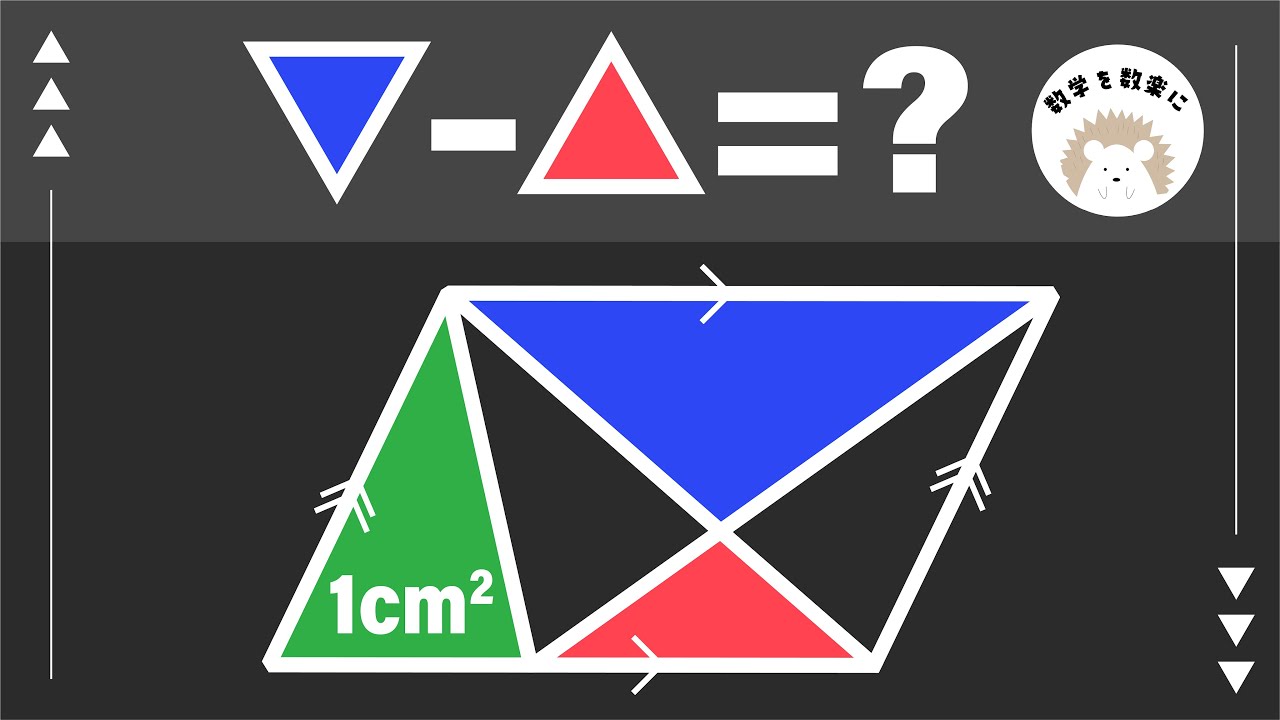
補助線引けるかな?気付けば一瞬!!
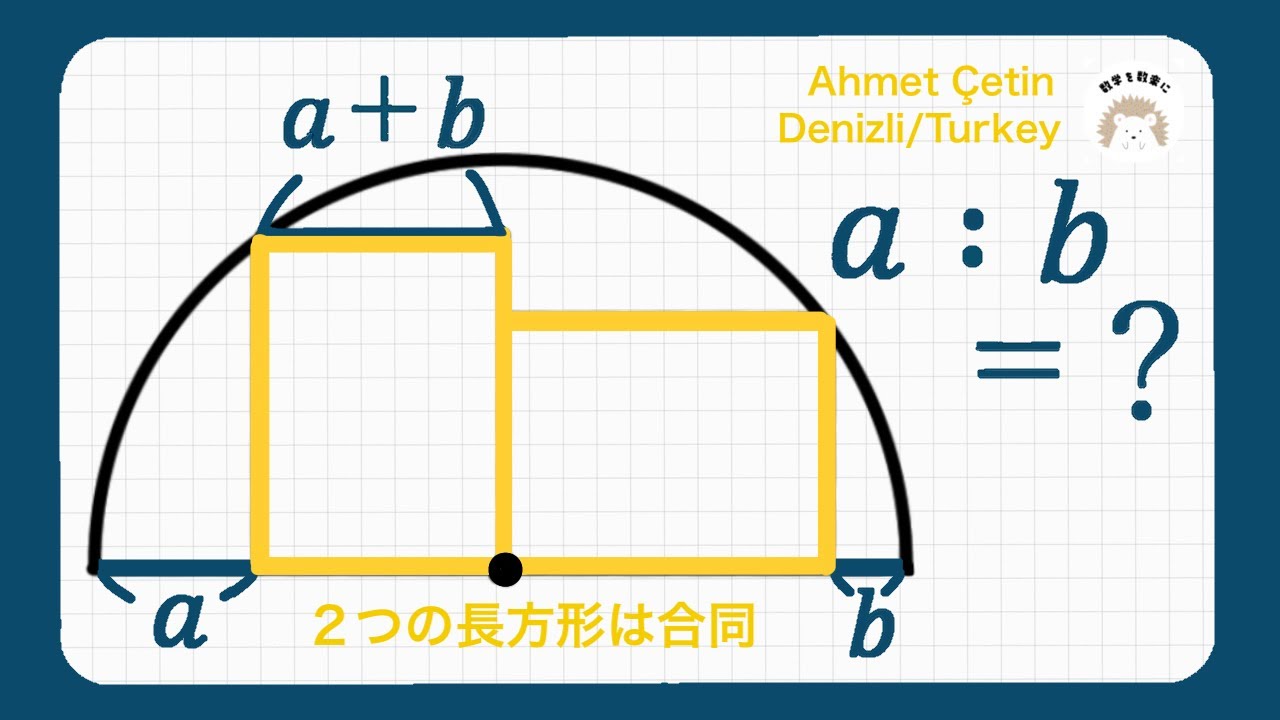
半円と2つの合同な長方形
単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2つの長方形は合同
a:b=?
*図は動画内参照
この動画を見る
2つの長方形は合同
a:b=?
*図は動画内参照
比を求める
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
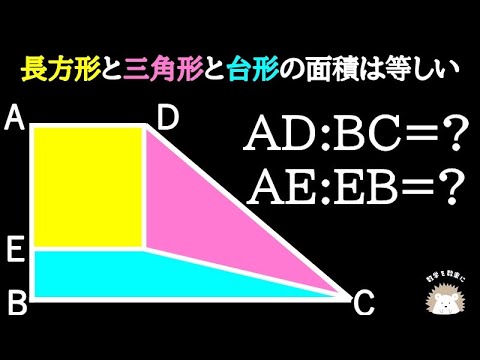
長方形と台形と三角形の面積が等しい
a:b=
x:y=
*図は動画内参照
この動画を見る
長方形と台形と三角形の面積が等しい
a:b=
x:y=
*図は動画内参照
正方形と円と正方形 算数です

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
*四角形は正方形
斜線部の面積は?
*図は動画内参照
この動画を見る
*四角形は正方形
斜線部の面積は?
*図は動画内参照
福田の数学・入試問題解説〜東北大学2022年文系第4問〜空間における四面体の高さと体積

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
xyz空間内の点O(0,0,0),$A(1,\sqrt2,\sqrt3),B(-\sqrt3,0,1),C(\sqrt6,-\sqrt3,\sqrt2)$
を頂点とする四面体OABCを考える。3点OABを含む平面からの距離が1の点
のうち、点Oに最も近く、x座標が正のものをHとする。
(1)Hの座標を求めよ。
(2)3点OABを含む平面と点Cの距離を求めよ。
(3)四面体OABCの体積を求めよ。
2022東北大学文系過去問
この動画を見る
xyz空間内の点O(0,0,0),$A(1,\sqrt2,\sqrt3),B(-\sqrt3,0,1),C(\sqrt6,-\sqrt3,\sqrt2)$
を頂点とする四面体OABCを考える。3点OABを含む平面からの距離が1の点
のうち、点Oに最も近く、x座標が正のものをHとする。
(1)Hの座標を求めよ。
(2)3点OABを含む平面と点Cの距離を求めよ。
(3)四面体OABCの体積を求めよ。
2022東北大学文系過去問
