 図形の性質
図形の性質
 図形の性質
図形の性質
正五角形と正三角形 京都府
福田のおもしろ数学012〜10秒チャレンジ〜重心によって分割される3つの三角形の面積が等しい証明

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
三角形において、その重心 G で分割された 3 つの三角形の面積は等しいことを証明せよ.
※図は動画内参照
この動画を見る
三角形において、その重心 G で分割された 3 つの三角形の面積は等しいことを証明せよ.
※図は動画内参照
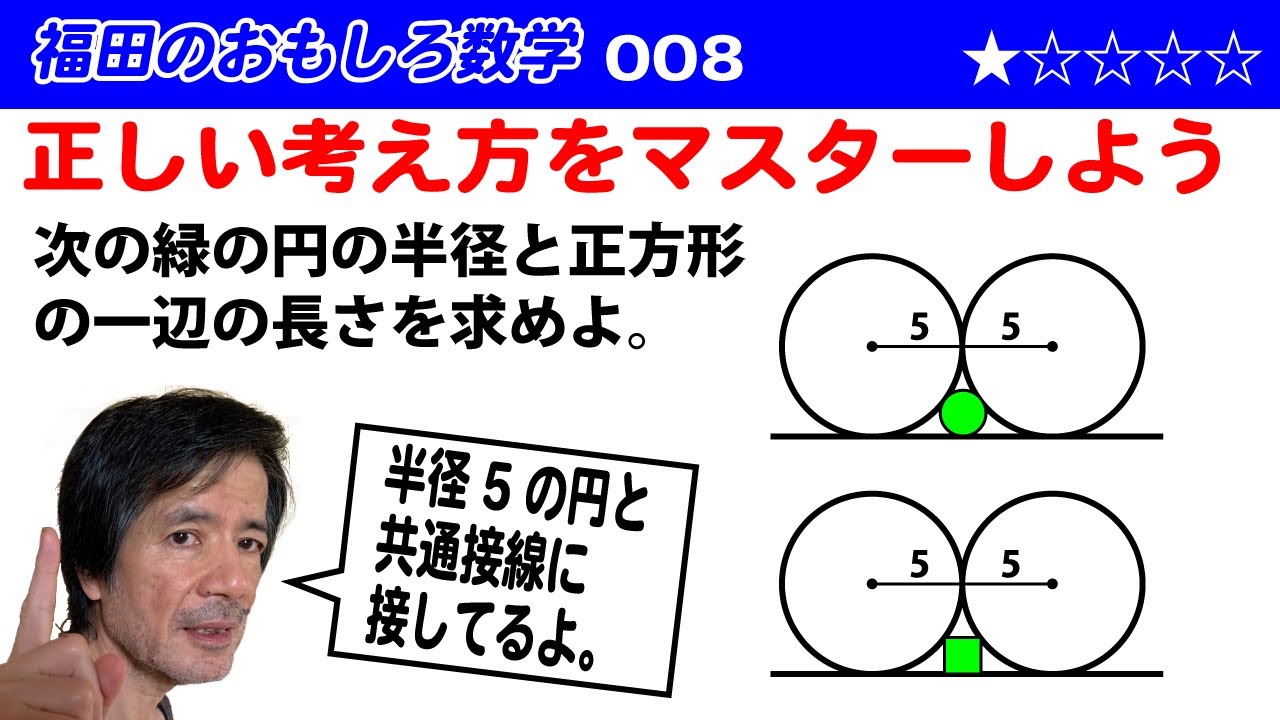
福田のおもしろ数学008〜正しいフォームを身につけよう〜外接する2円と共通接線に接する正方形
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の緑の円の半径と正方形の一片の長さを求めよ
※図は動画内参照
この動画を見る
次の緑の円の半径と正方形の一片の長さを求めよ
※図は動画内参照
正方形の面積2024
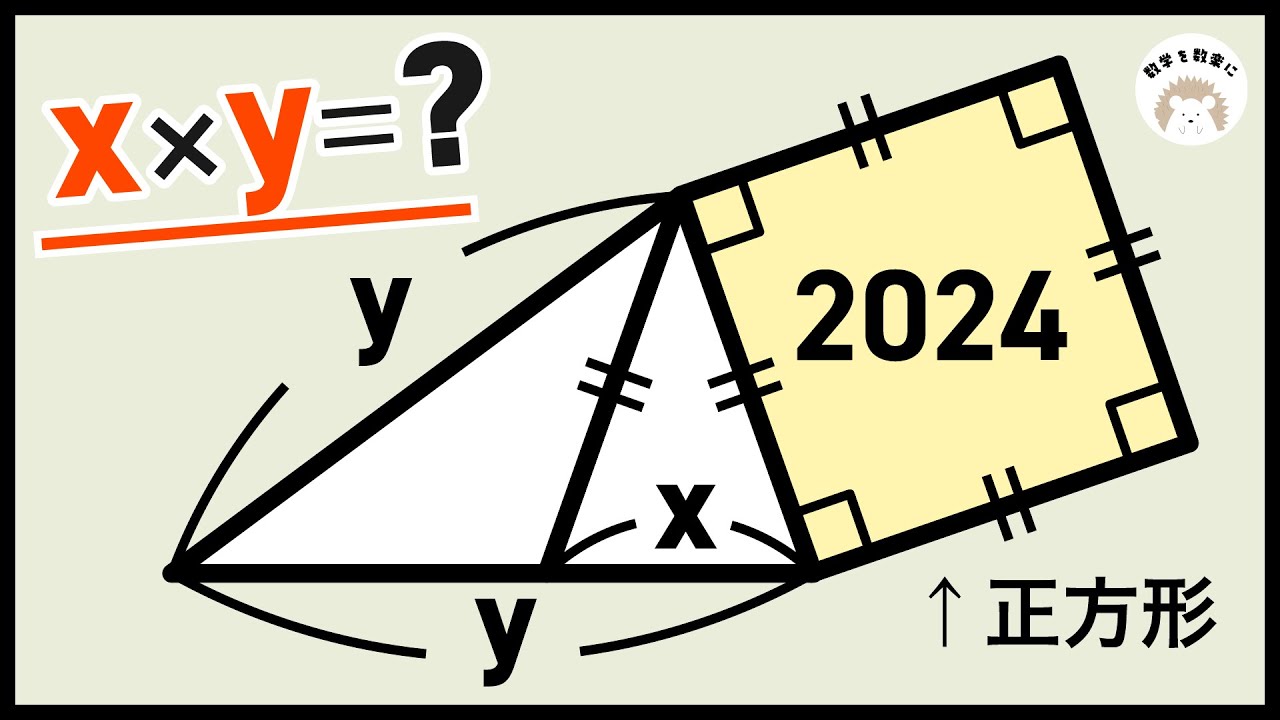
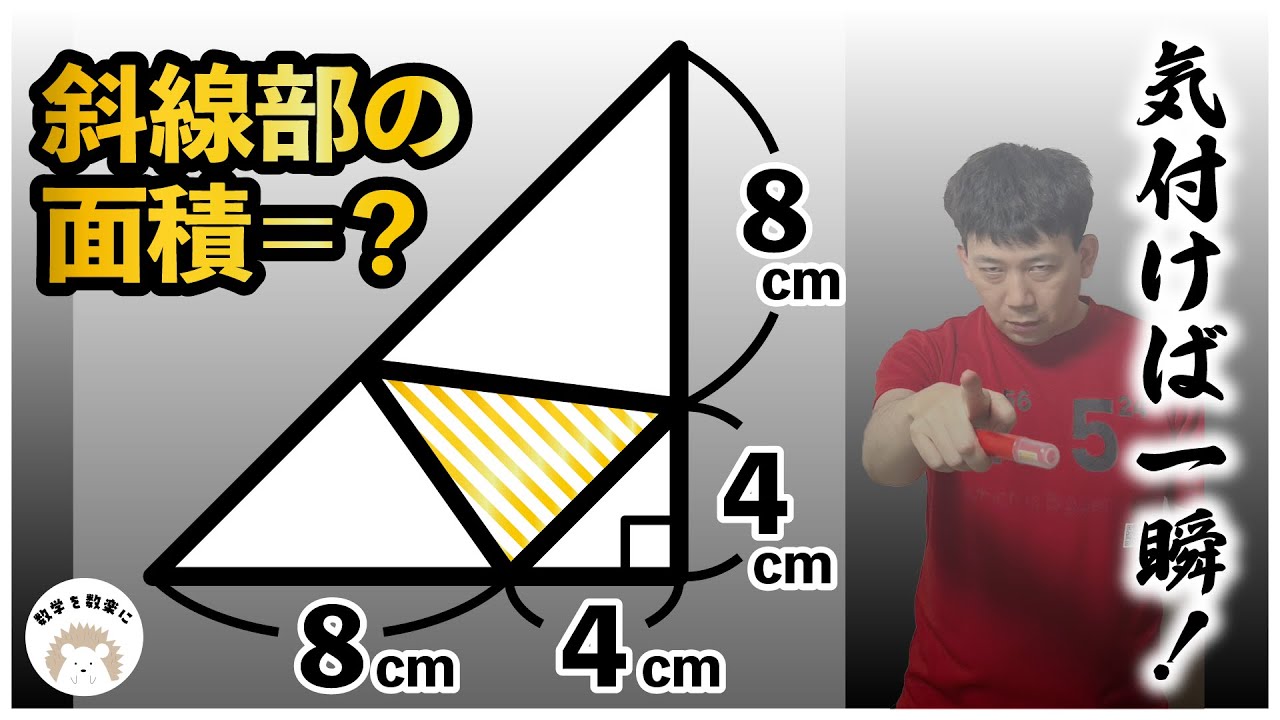
気付けば一瞬!!角の和

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a +\angle b +\angle c = ?$
*図は動画内参照
この動画を見る
$\angle a +\angle b +\angle c = ?$
*図は動画内参照
【共通テスト】数学IA 第5問図形の性質を解説してみました(2023年本試)【この動画だけ絶望的にわかりにくい】

単元:
#数A#図形の性質#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
動画内手順1の(Step 1)と(Step 4)により、4点C,G,H,[ウ]は同一円周上にあることが分かる。
よって、$\angle CHG =$[エ]である。
一方、点Eは円Oの周上にあることから、[エ]=[オ]がわかる。
よって、$\angle CHG =$[オ]であるので、4点C,G,H,[カ]は同一円周上にある。
この円が点[ウ]を通ることにより、$\angle OEH =$[アイ]$^{ \circ }$を示すことができる。
[ウ]の解答群
⓪B
①D
②F
③O
[エ]の解答群
⓪$\angle AEC$
①$\angle CDF$
②$\angle CGH$
③$\angle CBO$
④$\angle FOG$
[オ]の解答群
⓪$\angle AED$
①$\angle ADE$
②$\angle BOE$
③$\angle DEG$
④$\angle EOH$
[カ]の解答群
⓪A
①D
②E
③F
-----------------
動画内手順2のとき、$\angle PTS =$[キ]である。
円Oの半径が$\sqrt{ 5 }$で、$OT=3 \sqrt{ 6 }$であったとすると、3点O,P,Rを通る円の半径は$\displaystyle \frac{[ク]\sqrt{ [ケ] }}{[コ]}$であり、RT=[サ]である。
[キ]の解答群
⓪$\angle PQS$
①$\angle PST$
②$\angle QPS$
③$\angle QRS$
④$\angle SRT$
この動画を見る
動画内手順1の(Step 1)と(Step 4)により、4点C,G,H,[ウ]は同一円周上にあることが分かる。
よって、$\angle CHG =$[エ]である。
一方、点Eは円Oの周上にあることから、[エ]=[オ]がわかる。
よって、$\angle CHG =$[オ]であるので、4点C,G,H,[カ]は同一円周上にある。
この円が点[ウ]を通ることにより、$\angle OEH =$[アイ]$^{ \circ }$を示すことができる。
[ウ]の解答群
⓪B
①D
②F
③O
[エ]の解答群
⓪$\angle AEC$
①$\angle CDF$
②$\angle CGH$
③$\angle CBO$
④$\angle FOG$
[オ]の解答群
⓪$\angle AED$
①$\angle ADE$
②$\angle BOE$
③$\angle DEG$
④$\angle EOH$
[カ]の解答群
⓪A
①D
②E
③F
-----------------
動画内手順2のとき、$\angle PTS =$[キ]である。
円Oの半径が$\sqrt{ 5 }$で、$OT=3 \sqrt{ 6 }$であったとすると、3点O,P,Rを通る円の半径は$\displaystyle \frac{[ク]\sqrt{ [ケ] }}{[コ]}$であり、RT=[サ]である。
[キ]の解答群
⓪$\angle PQS$
①$\angle PST$
②$\angle QPS$
③$\angle QRS$
④$\angle SRT$
六角形バリアは不可能じゃね?

単元:
#図形の性質#空間における垂直と平行と多面体(オイラーの法則)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
葬送のフリーレンのバリアなどで六角形で球を作っている件に関して解説していきます。
この動画を見る
葬送のフリーレンのバリアなどで六角形で球を作っている件に関して解説していきます。
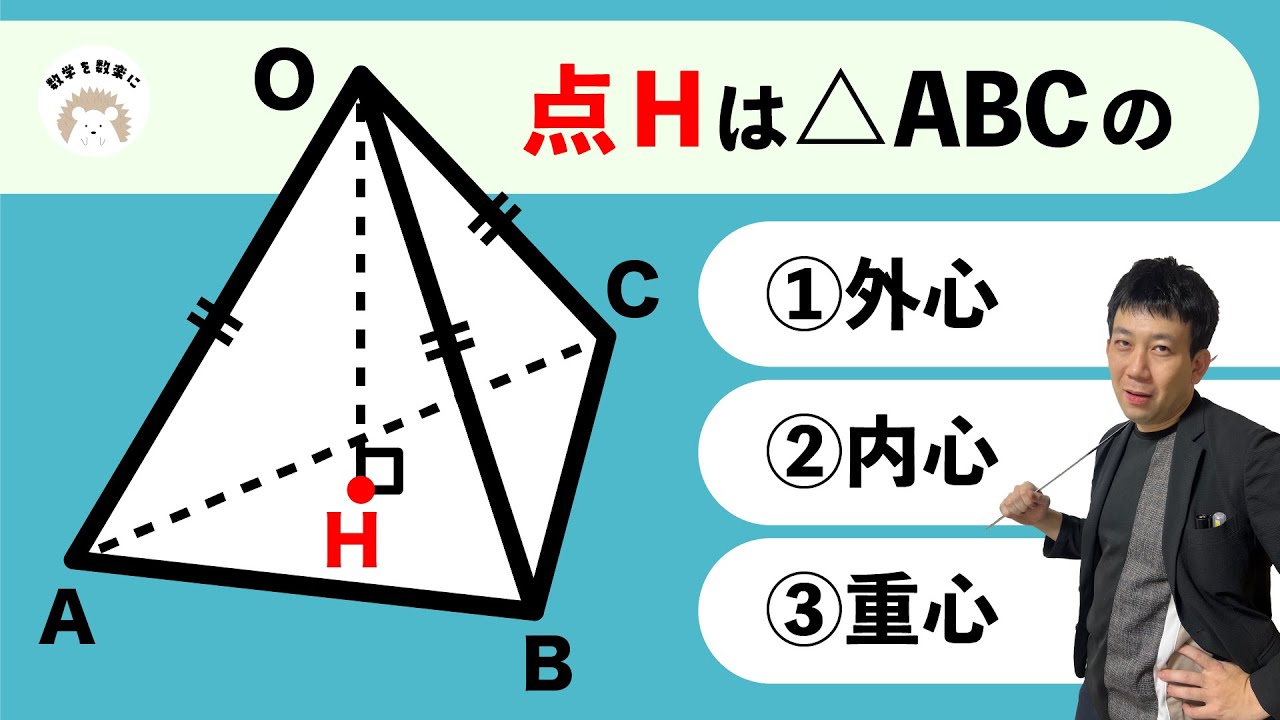
重心ではありませんよ。
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Hは△ABCの
①外心
②内心
③重心
*図は動画内参照
この動画を見る
点Hは△ABCの
①外心
②内心
③重心
*図は動画内参照
垂直二等分線の交点が一点で交わるのはなぜ?

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
各辺の垂直二等分線の交点が1点で交わるのはなぜ?
*図は動画内参照
この動画を見る
各辺の垂直二等分線の交点が1点で交わるのはなぜ?
*図は動画内参照
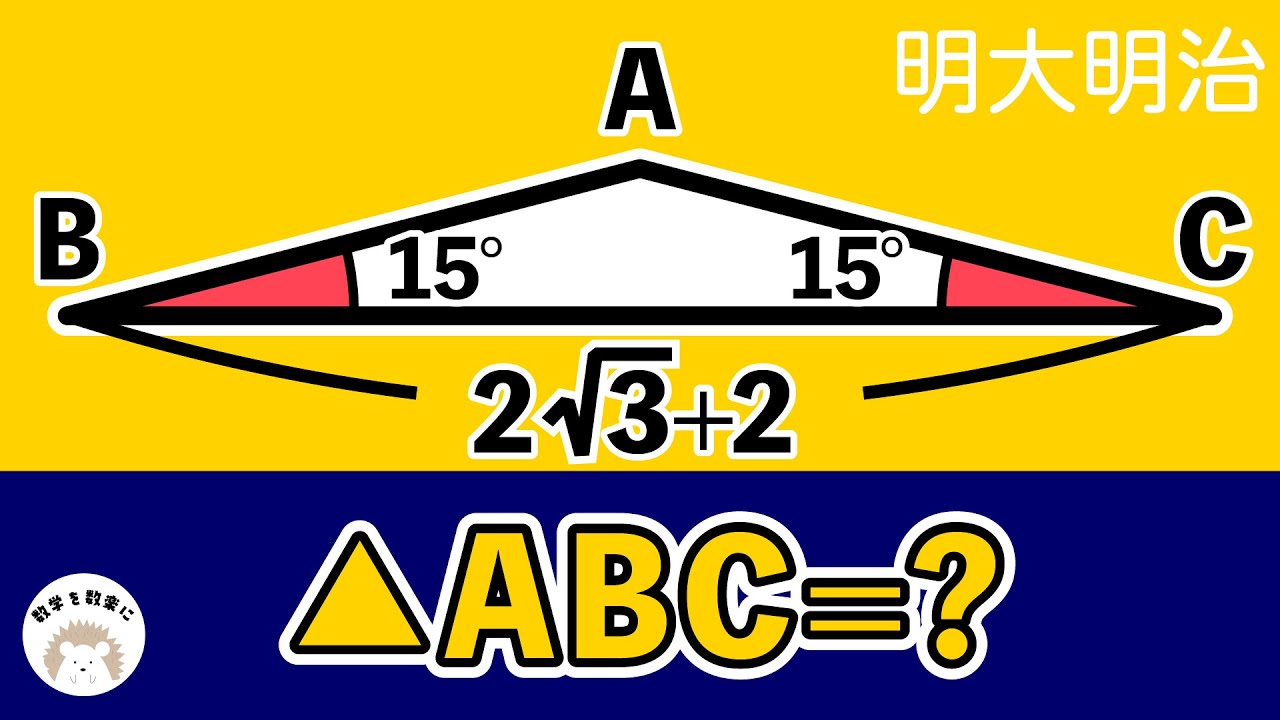
15度15度150度の二等辺三角形 明大明治
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=?
*図は動画内参照
明治大学付属明治高等学校
この動画を見る
△ABC=?
*図は動画内参照
明治大学付属明治高等学校
22.5°
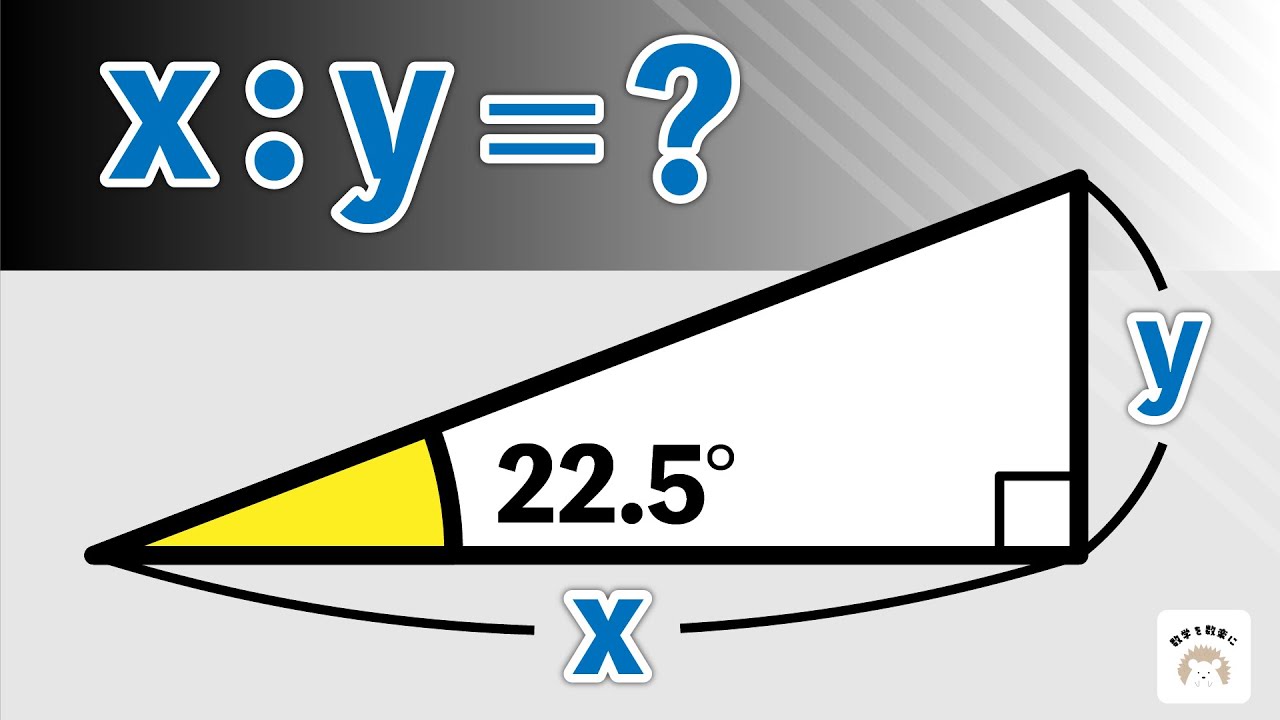
22.5°
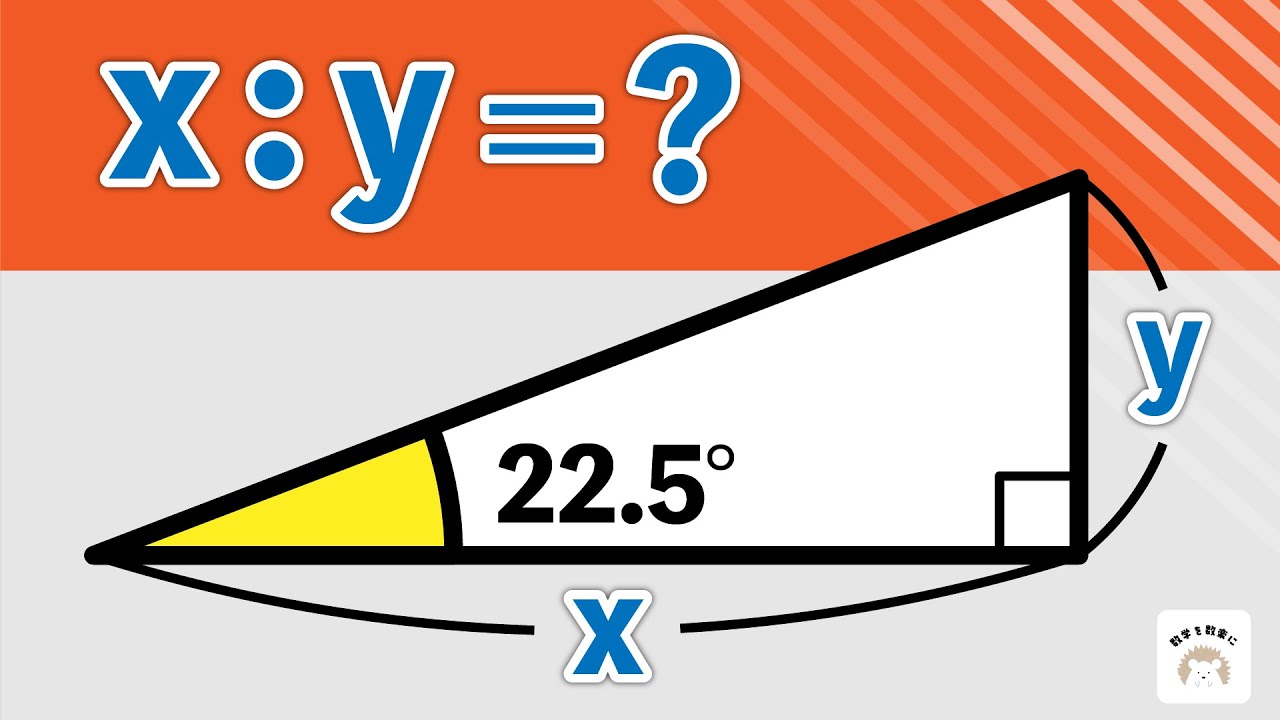
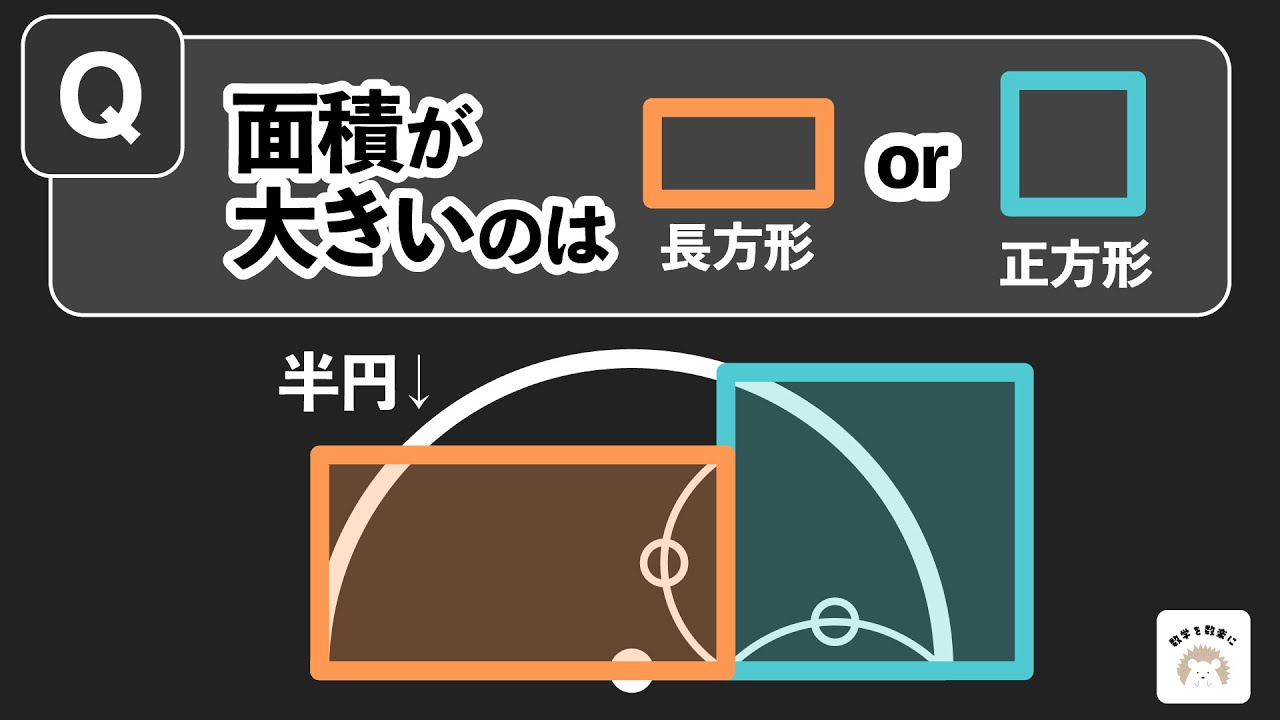
これだけでわかるの?面積が大きいのはどっち?
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
面積が大きいのは長方形 or 正方形
*図は動画内参照
この動画を見る
面積が大きいのは長方形 or 正方形
*図は動画内参照
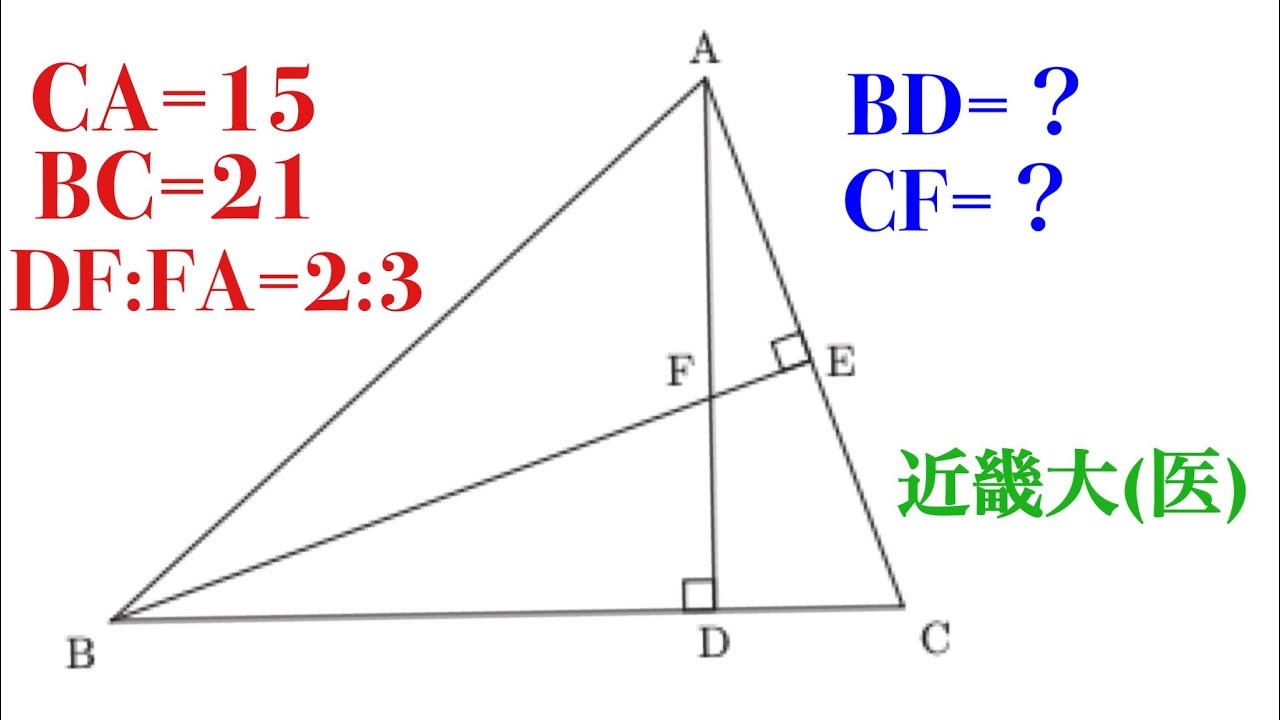
近畿大(医)メネラウスの定理の証明もやるよ
単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
BC=21 DF:FA=2:3のとき、CFは?
近畿大(医)過去問
この動画を見る
BC=21 DF:FA=2:3のとき、CFは?
近畿大(医)過去問
外角の二等分線と平行 奈良学園
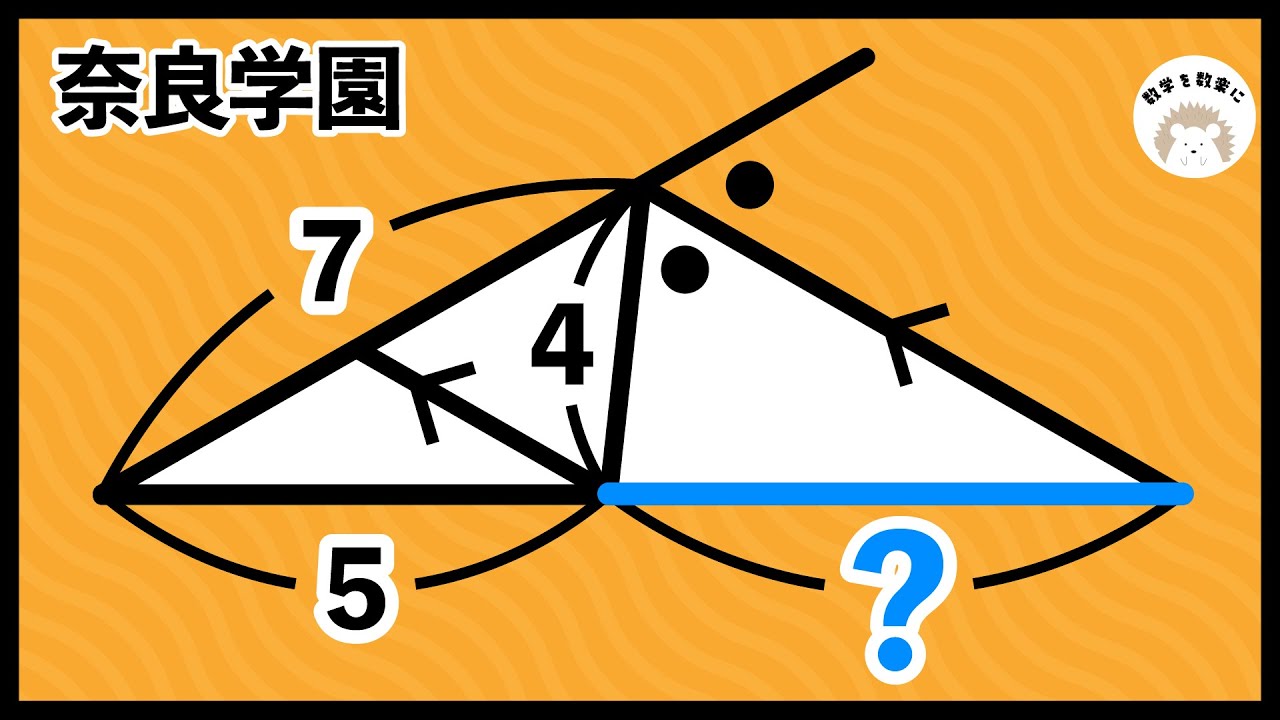
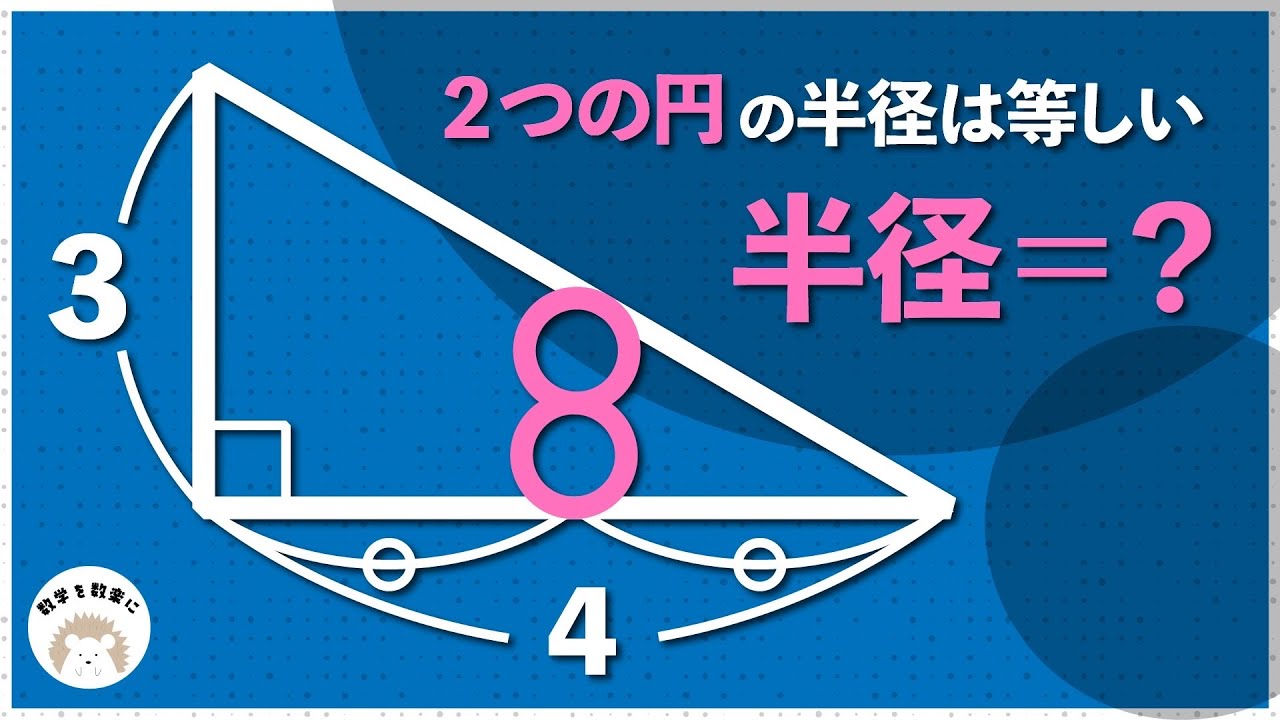
直角三角形と二つの円
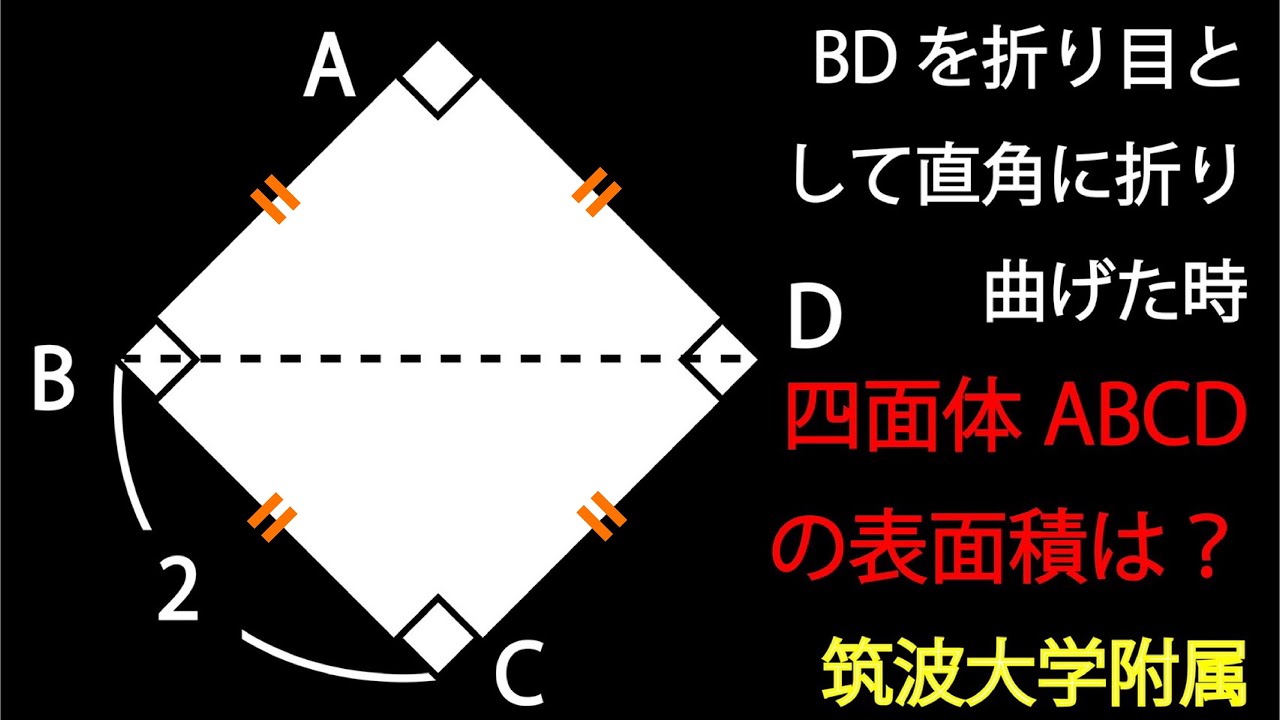
正方形を折り曲げる 筑波大附属
単元:
#数A#図形の性質#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BDを折り目として直角に折り曲げた時四面体ABCDの表面積は?
*図は動画内参照
筑波大学付属高等学校
この動画を見る
BDを折り目として直角に折り曲げた時四面体ABCDの表面積は?
*図は動画内参照
筑波大学付属高等学校
福田の数学〜三角比の基本の復習にどうぞ〜慶應義塾大学2023年経済学部第1問(1)〜三角形と外接円内接円の半径

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)$\triangle ABC$において
$sinA:sinB:sinC=3:7:8$
が成り立つとき、ある性の実数kを用いて
$a=\fbox{ア}k,b=\fbox{イ}k,c=\fbox{ウ}k$
と表すことができるので、この三角形の最も大きい角の余弦の値は$-\dfrac{\fbox{エ}}{\fbox{オ}}$であり、正弦の値は$-\fbox{カ}\sqrt{\fbox{キ}}$である。さらに$\triangle ABC$の面積が$54\sqrt{3}$であるとき、$k=\fbox{ク}$となるので、この三角形の外接円の半径は$\fbox{ケ}\sqrt{\fbox{コ}}$であり、内接円の半径は$\fbox{サ}\sqrt{\fbox{シ}}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
(1)$\triangle ABC$において
$sinA:sinB:sinC=3:7:8$
が成り立つとき、ある性の実数kを用いて
$a=\fbox{ア}k,b=\fbox{イ}k,c=\fbox{ウ}k$
と表すことができるので、この三角形の最も大きい角の余弦の値は$-\dfrac{\fbox{エ}}{\fbox{オ}}$であり、正弦の値は$-\fbox{カ}\sqrt{\fbox{キ}}$である。さらに$\triangle ABC$の面積が$54\sqrt{3}$であるとき、$k=\fbox{ク}$となるので、この三角形の外接円の半径は$\fbox{ケ}\sqrt{\fbox{コ}}$であり、内接円の半径は$\fbox{サ}\sqrt{\fbox{シ}}$である。
2023慶應義塾大学経済学部過去問
気付けば一瞬!!正八角形と正方形

どっちが長い?
気付けば一瞬!?立方体の中の三角形の面積
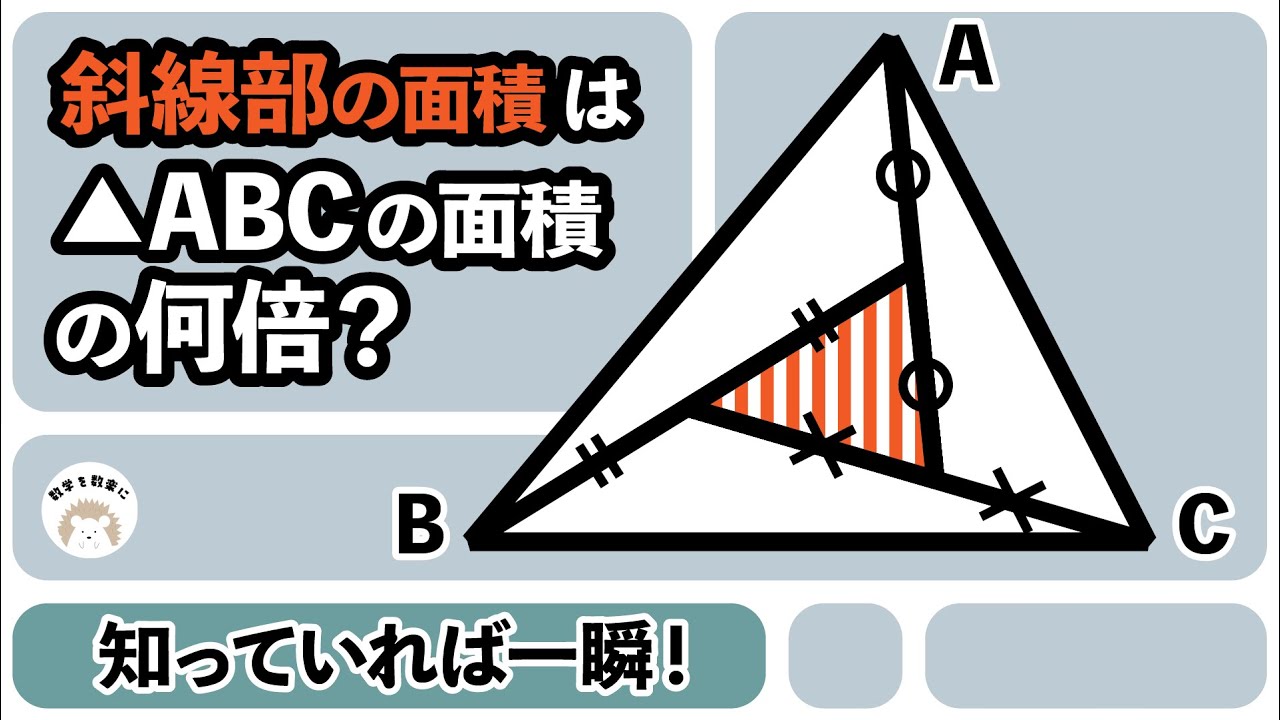
面積比!!知っていれば一瞬!!知ってなくても一瞬!?
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△DEFの面積は△ABCの面積の何倍?
*図は動画内参照
この動画を見る
△DEFの面積は△ABCの面積の何倍?
*図は動画内参照
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
小学生も解ける!? 2通りで解説 角度
気付けば一瞬!!面積
回転体の体積 立教新座

福田の数学〜共通テスト対策にもってこい〜明治大学2023年全学部統一ⅠⅡAB第3問〜四面体の体積
単元:
#数A#大学入試過去問(数学)#図形の性質#センター試験・共通テスト関連#学校別大学入試過去問解説(数学)#共通テスト#空間における垂直と平行と多面体(オイラーの法則)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
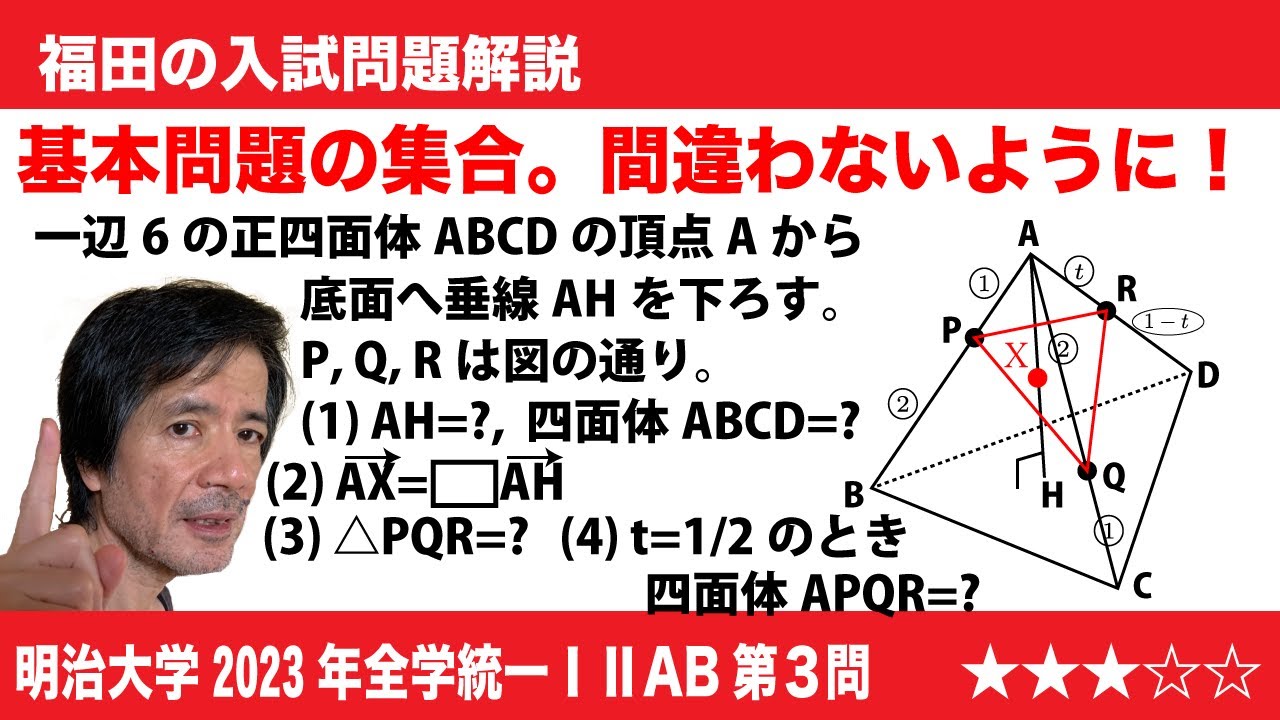
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
この動画を見る
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
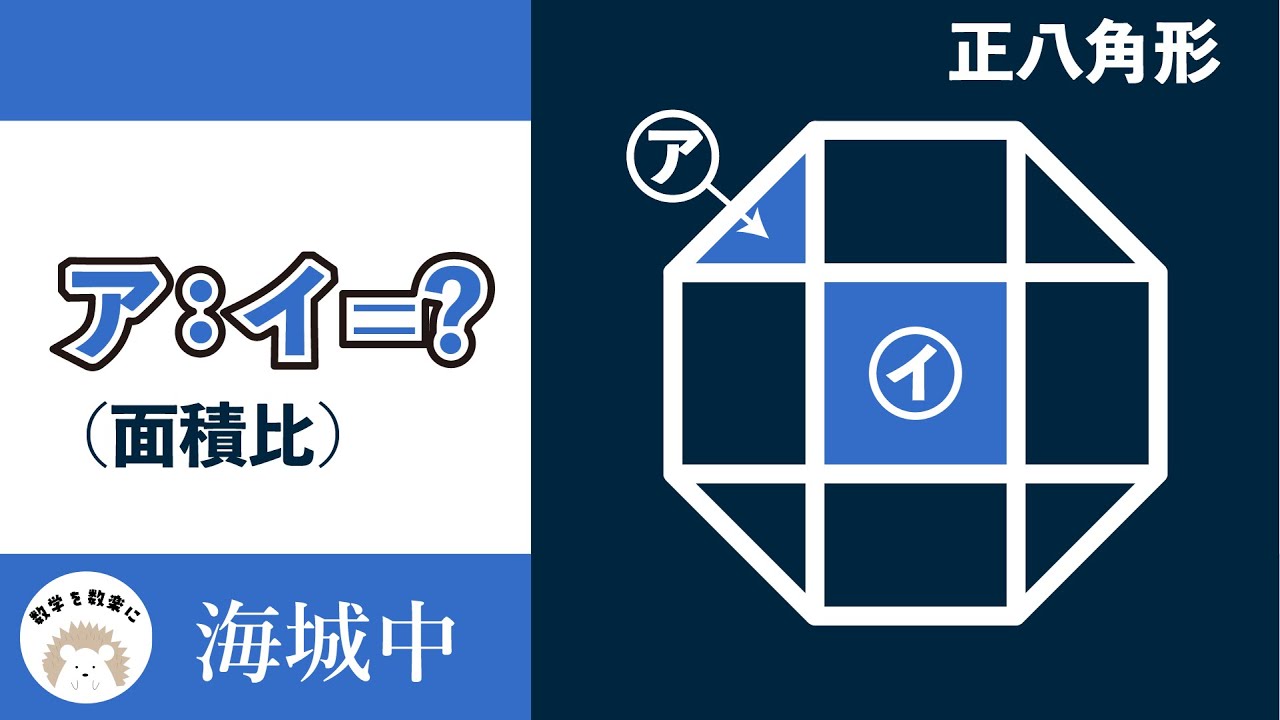
正八角形 面積比 海城中
気付けば一瞬!!正方形の面積

外心と内心が一致する三角形はどんな三角形?

