 図形の性質
図形の性質
 図形の性質
図形の性質
おうぎ形の面積 数学YouTuberが今流行りの数学YouTuberについて語る

2023高校入試解説17問目 3つの内接円 渋谷教育学園幕張
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
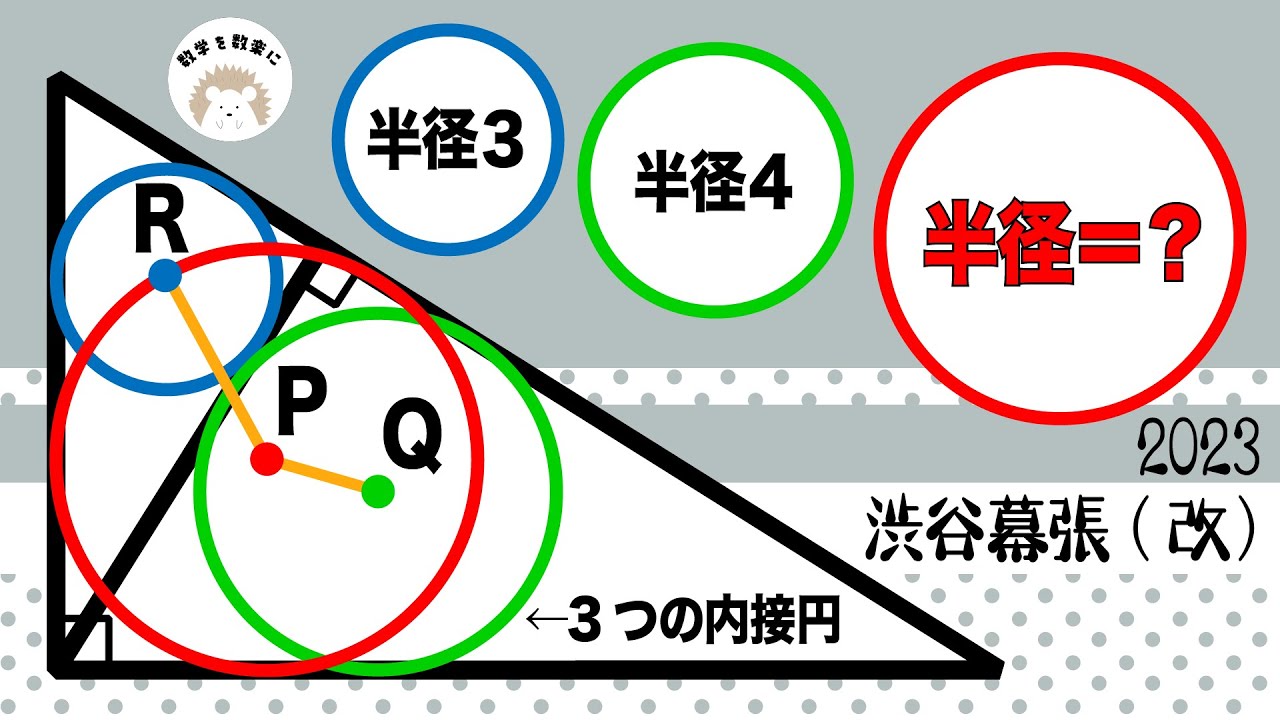
青○:半径3
緑○:半径4
赤○:半径=?
*図は動画内参照
2023渋谷教育学園幕張高等学校(改)
この動画を見る
青○:半径3
緑○:半径4
赤○:半径=?
*図は動画内参照
2023渋谷教育学園幕張高等学校(改)
福田の数学〜2023年共通テスト速報〜数学IA第5問図形の性質〜作図によって描いた図形の性質

単元:
#数A#図形の性質#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
【第5問】
(1) 円Oに対して、次の手順1で作図を行う。
[手順1]
(Step 1) 円Oと異なる2点で交わり、中心Oを通らない直線lを引く。円Oと直線lとの交点をA, Bとし、線分ABの中点Cをとる。
(Step 2) 円Oの周上に、点Dを$\angle COD$が鈍角となるようにとる。直線CDを引き、円Oとの交点でDとは異なる点をEとする。
(Step 3) 点Dを通り直線OCに垂直な直線を引き、直線OCとの交点をFとし、円Oとの交点でDとは異なる点をGとする。
(Step 4) 点Gにおける円Oの接線を引き、直線lとの交点をHとする。
このとき、直線lと点Dの位置によらず、直線EHは円Oの接線である。このことは、次の構想に基づいて、後のように説明できる。
[構想]
直線EHが円Oの接線であることを証明するためには、$\angle OEH=\boxed{\ \ アイ\ \ }°$であることを示せばよい。
手順1の(Step 1)と(Step 4)により、4点C, G, H, $\boxed{\boxed{\ \ ウ\ \ }}$は同一円周上にあることがわかる。よって、$\angle CHG=\boxed{\boxed{\ \ エ\ \ }}$である。一方、点Eは円Oの周上にあることから、$\boxed{\boxed{\ \ エ\ \ }}=\boxed{\boxed{\ \ オ\ \ }}$がわかる。よって、$\angle CHG=\boxed{\boxed{\ \ オ\ \ }}$であるので、4点C, G, H, $\boxed{\boxed{\ \ カ\ \ }}$は同一円周上にある。この円が点$\boxed{\boxed{\ \ ウ\ \ }}$を通ることにより、$\angle OEH=\boxed{\ \ アイ\ \ }°$を示すことができる。
$\boxed{\boxed{\ \ ウ\ \ }}$の解答群
⓪B ①D ②F ③O
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪$\angle AFC$ ①$\angle CDF$ ②$\angle CGH$ ③$\angle CBO$ ④$\angle FOG$
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$\angle AED$ ①$\angle ADE$ ②$\angle BOE$ ③$\angle DEG$ ④$\angle EOH$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪A ①D ②E ③F
(2) 円Oに対して、(1)の手順1とは直線lの引き方を変え、次の手順2で作図を行う。
[手順2]
(Step 1) 円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
(Step 2) 円Oの周上に、点Qを$\angle POQ$が鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
(Step 3) 点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
(Step 4) 点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、$\angle PTS=\boxed{\boxed{\ \ キ\ \ }}$である。
円Oの半径が$\sqrt 5$で、OT=$3\sqrt 6$であったとすると、3点O, P, Rを通る円の半径は$\frac{\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}}{\boxed{\ \ コ\ \ }}$であり、RT=$\boxed{\ \ サ\ \ }$である。
$\boxed{\boxed{\ \ キ\ \ }}$の解答群
⓪$\angle PQS$ ①$\angle PST$ ②$\angle QPS$ ③$\angle QRS$ ④$\angle SRT$
2023共通テスト過去問
この動画を見る
【第5問】
(1) 円Oに対して、次の手順1で作図を行う。
[手順1]
(Step 1) 円Oと異なる2点で交わり、中心Oを通らない直線lを引く。円Oと直線lとの交点をA, Bとし、線分ABの中点Cをとる。
(Step 2) 円Oの周上に、点Dを$\angle COD$が鈍角となるようにとる。直線CDを引き、円Oとの交点でDとは異なる点をEとする。
(Step 3) 点Dを通り直線OCに垂直な直線を引き、直線OCとの交点をFとし、円Oとの交点でDとは異なる点をGとする。
(Step 4) 点Gにおける円Oの接線を引き、直線lとの交点をHとする。
このとき、直線lと点Dの位置によらず、直線EHは円Oの接線である。このことは、次の構想に基づいて、後のように説明できる。
[構想]
直線EHが円Oの接線であることを証明するためには、$\angle OEH=\boxed{\ \ アイ\ \ }°$であることを示せばよい。
手順1の(Step 1)と(Step 4)により、4点C, G, H, $\boxed{\boxed{\ \ ウ\ \ }}$は同一円周上にあることがわかる。よって、$\angle CHG=\boxed{\boxed{\ \ エ\ \ }}$である。一方、点Eは円Oの周上にあることから、$\boxed{\boxed{\ \ エ\ \ }}=\boxed{\boxed{\ \ オ\ \ }}$がわかる。よって、$\angle CHG=\boxed{\boxed{\ \ オ\ \ }}$であるので、4点C, G, H, $\boxed{\boxed{\ \ カ\ \ }}$は同一円周上にある。この円が点$\boxed{\boxed{\ \ ウ\ \ }}$を通ることにより、$\angle OEH=\boxed{\ \ アイ\ \ }°$を示すことができる。
$\boxed{\boxed{\ \ ウ\ \ }}$の解答群
⓪B ①D ②F ③O
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪$\angle AFC$ ①$\angle CDF$ ②$\angle CGH$ ③$\angle CBO$ ④$\angle FOG$
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$\angle AED$ ①$\angle ADE$ ②$\angle BOE$ ③$\angle DEG$ ④$\angle EOH$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪A ①D ②E ③F
(2) 円Oに対して、(1)の手順1とは直線lの引き方を変え、次の手順2で作図を行う。
[手順2]
(Step 1) 円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
(Step 2) 円Oの周上に、点Qを$\angle POQ$が鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
(Step 3) 点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
(Step 4) 点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、$\angle PTS=\boxed{\boxed{\ \ キ\ \ }}$である。
円Oの半径が$\sqrt 5$で、OT=$3\sqrt 6$であったとすると、3点O, P, Rを通る円の半径は$\frac{\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}}{\boxed{\ \ コ\ \ }}$であり、RT=$\boxed{\ \ サ\ \ }$である。
$\boxed{\boxed{\ \ キ\ \ }}$の解答群
⓪$\angle PQS$ ①$\angle PST$ ②$\angle QPS$ ③$\angle QRS$ ④$\angle SRT$
2023共通テスト過去問
2023高校入試解説12問目 台形と半円 解き方2通り 日大習志野(改)

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
この動画を見る
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
角の二等分線➕平行線=❓

福田の1.5倍速演習〜合格する重要問題059〜慶應義塾大学2019年度薬学部第1問(7)〜球に内接する四角錐の体積の最大値

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (7)正四角錐ABCDEの全ての頂点は半径3の球面上にある。
この正四角錐の体積Vの最大値は$\boxed{\ \ ソ\ \ }$である。
2019慶應義塾大学薬学部過去問
この動画を見る
$\Large{\boxed{1}}$ (7)正四角錐ABCDEの全ての頂点は半径3の球面上にある。
この正四角錐の体積Vの最大値は$\boxed{\ \ ソ\ \ }$である。
2019慶應義塾大学薬学部過去問
2023高校入試解説8問目 内接円 西大和学園 内接円

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC∽△PRQ
△PRQ=?
*図は動画内参照
2023西大和学園高等学校
この動画を見る
△ABC∽△PRQ
△PRQ=?
*図は動画内参照
2023西大和学園高等学校
福田の1.5倍速演習〜合格する重要問題058〜慶應義塾大学2019年度環境情報学部第5問〜正方形の中の内接外接する円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ 図のように(※動画参照)、1つの正方形の中に、半径の異なる3種類の円が合計10個配置されている。
円$A_1$と$A_2$は半径が同じRで、それぞれ図のように正方形の2辺に内接している。
円$B_1,B_2,B_3,B_4,B_5,B_6$は半径が同じrで、円$B_1$と$B_2$は接し、
図のように両方とも円$A_1$に内接し円$A_2$に外接している。円$B_3$と$B_4$は接し、図のように両方とも円$A_1$と円$A_2$に内接している。円$B_5$と$B_6$は接し、
図のように両方とも円$A_1$に外接し円$A_2$に内接している。
円$C_1$と$C_2$は半径が同じ$r'$で、それぞれ図のように正方形の2辺に内接し、円$A_1$と$A_2$に外接している。なお、円$B_1,B_2,B_5,B_6$は正方形の辺に接していない。
このとき、正方形の1辺の長さをsとすると
$\left\{\begin{array}{1}
R=\displaystyle\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}r \\
s=\left(\boxed{\ \ オカ\ \ }\sqrt{R}+\boxed{\ \ キク\ \ }\sqrt{r'}\right)^{\boxed{ケコ}}\\
r'=\frac{\boxed{\ \ サシ\ \ }+\displaystyle\sqrt{10}+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }+\displaystyle5\sqrt{10}}}{\boxed{\ \ チツ\ \ }}r\\
\end{array}\right.$
である。
2019慶應義塾大学環境情報学部過去問
この動画を見る
$\Large{\boxed{5}}$ 図のように(※動画参照)、1つの正方形の中に、半径の異なる3種類の円が合計10個配置されている。
円$A_1$と$A_2$は半径が同じRで、それぞれ図のように正方形の2辺に内接している。
円$B_1,B_2,B_3,B_4,B_5,B_6$は半径が同じrで、円$B_1$と$B_2$は接し、
図のように両方とも円$A_1$に内接し円$A_2$に外接している。円$B_3$と$B_4$は接し、図のように両方とも円$A_1$と円$A_2$に内接している。円$B_5$と$B_6$は接し、
図のように両方とも円$A_1$に外接し円$A_2$に内接している。
円$C_1$と$C_2$は半径が同じ$r'$で、それぞれ図のように正方形の2辺に内接し、円$A_1$と$A_2$に外接している。なお、円$B_1,B_2,B_5,B_6$は正方形の辺に接していない。
このとき、正方形の1辺の長さをsとすると
$\left\{\begin{array}{1}
R=\displaystyle\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}r \\
s=\left(\boxed{\ \ オカ\ \ }\sqrt{R}+\boxed{\ \ キク\ \ }\sqrt{r'}\right)^{\boxed{ケコ}}\\
r'=\frac{\boxed{\ \ サシ\ \ }+\displaystyle\sqrt{10}+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }+\displaystyle5\sqrt{10}}}{\boxed{\ \ チツ\ \ }}r\\
\end{array}\right.$
である。
2019慶應義塾大学環境情報学部過去問
2023高校入試解説6問目 座標平面上の正三角形 西大和学園
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
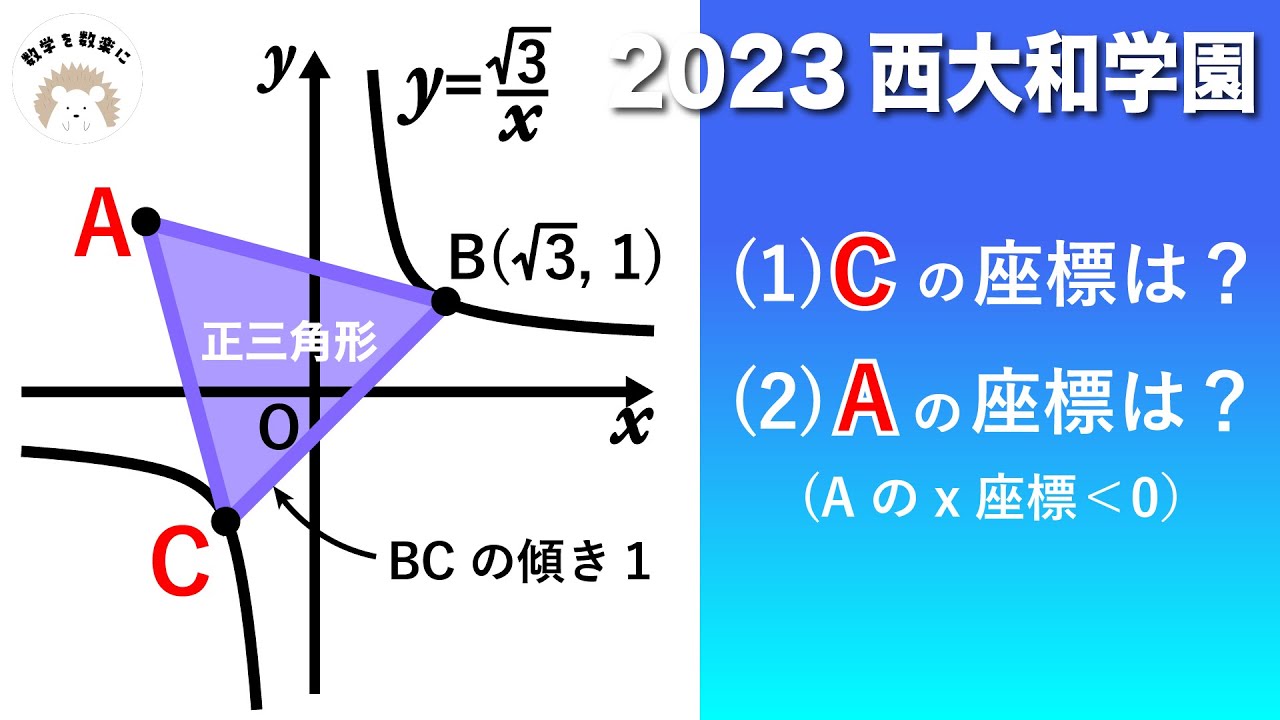
(1)Cの座標は?
(2)Aの座標は?
(Aのx座標<0)
*図は動画内参照
2023西大和学園高等学校
この動画を見る
(1)Cの座標は?
(2)Aの座標は?
(Aのx座標<0)
*図は動画内参照
2023西大和学園高等学校
面積二等分する直線を選べ!!大阪府
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
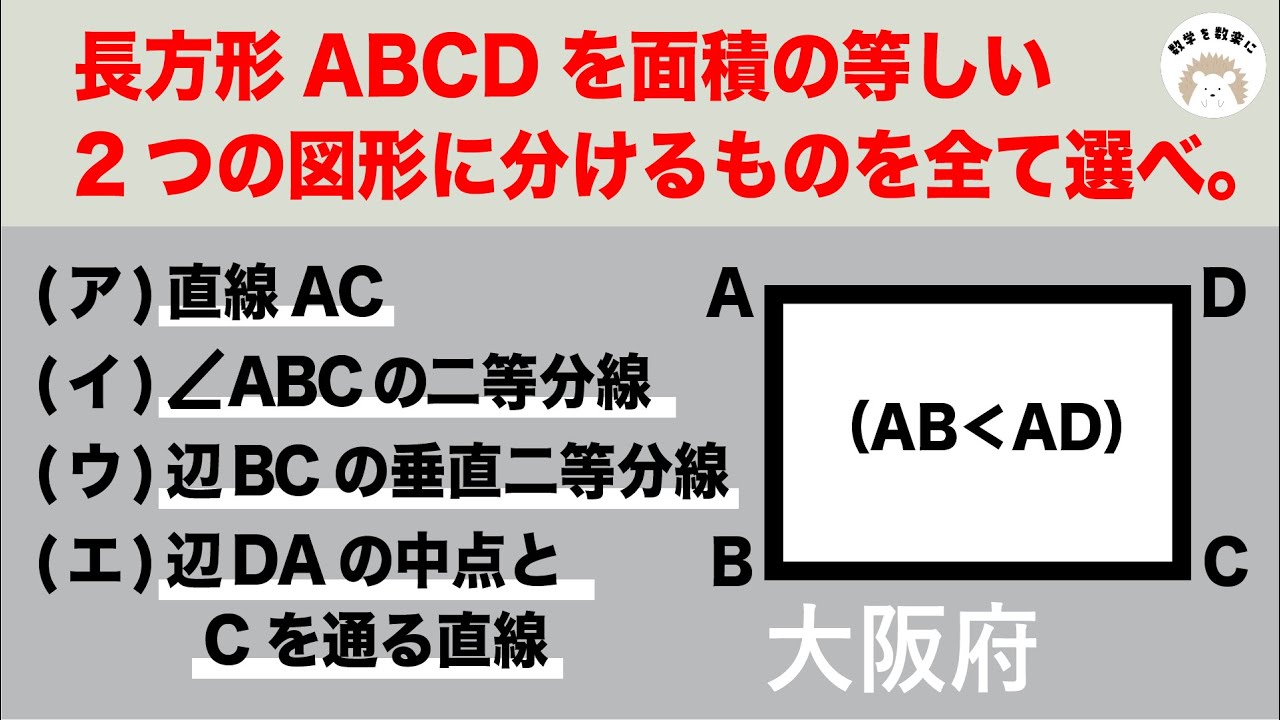
長方形ABCDを面積の等しい2つの図形に分けるものを全て選べ。
(ア)直線AC
(イ)$\angle ABC$の二等分線
(ウ)辺BCの垂直二等分線
(エ)辺DAの中点とCを通る直線
*図は動画内参照
大阪府
この動画を見る
長方形ABCDを面積の等しい2つの図形に分けるものを全て選べ。
(ア)直線AC
(イ)$\angle ABC$の二等分線
(ウ)辺BCの垂直二等分線
(エ)辺DAの中点とCを通る直線
*図は動画内参照
大阪府
球が出てきただけでビビるなよ。海城高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
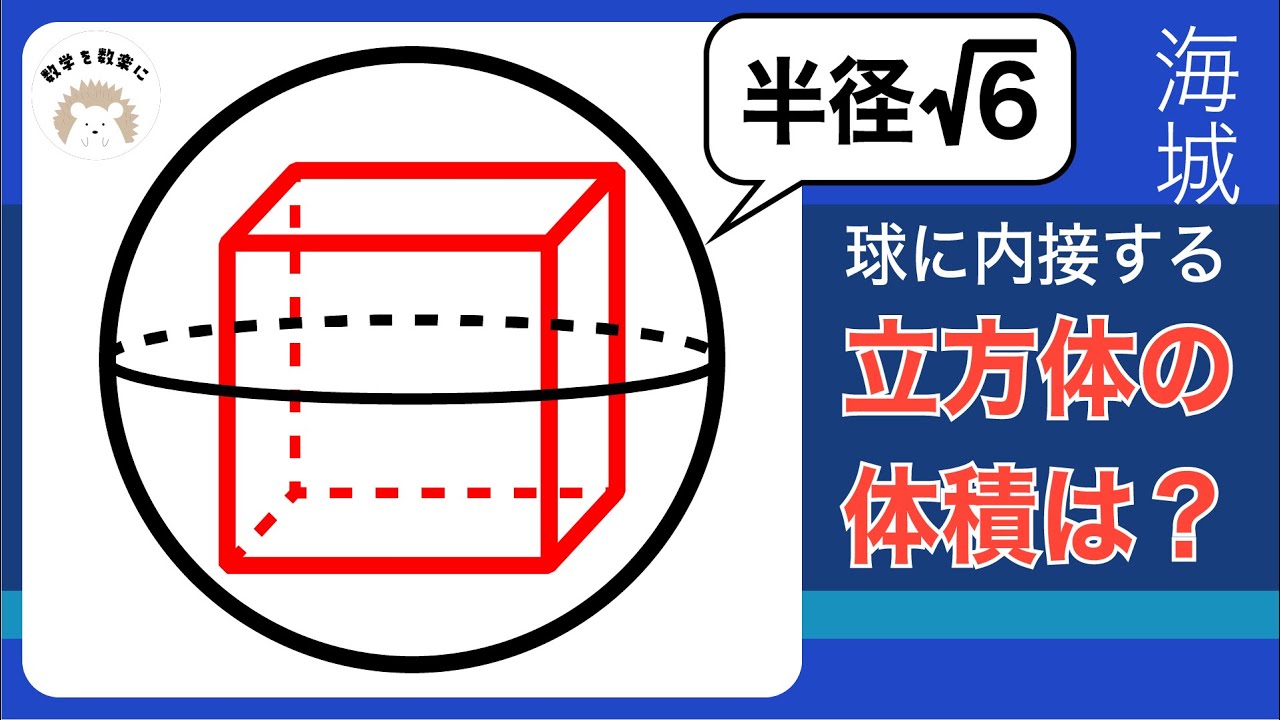
半径$\sqrt 6$の球に内接する立方体の体積=?
*図は動画内参照
海城高等学校
この動画を見る
半径$\sqrt 6$の球に内接する立方体の体積=?
*図は動画内参照
海城高等学校
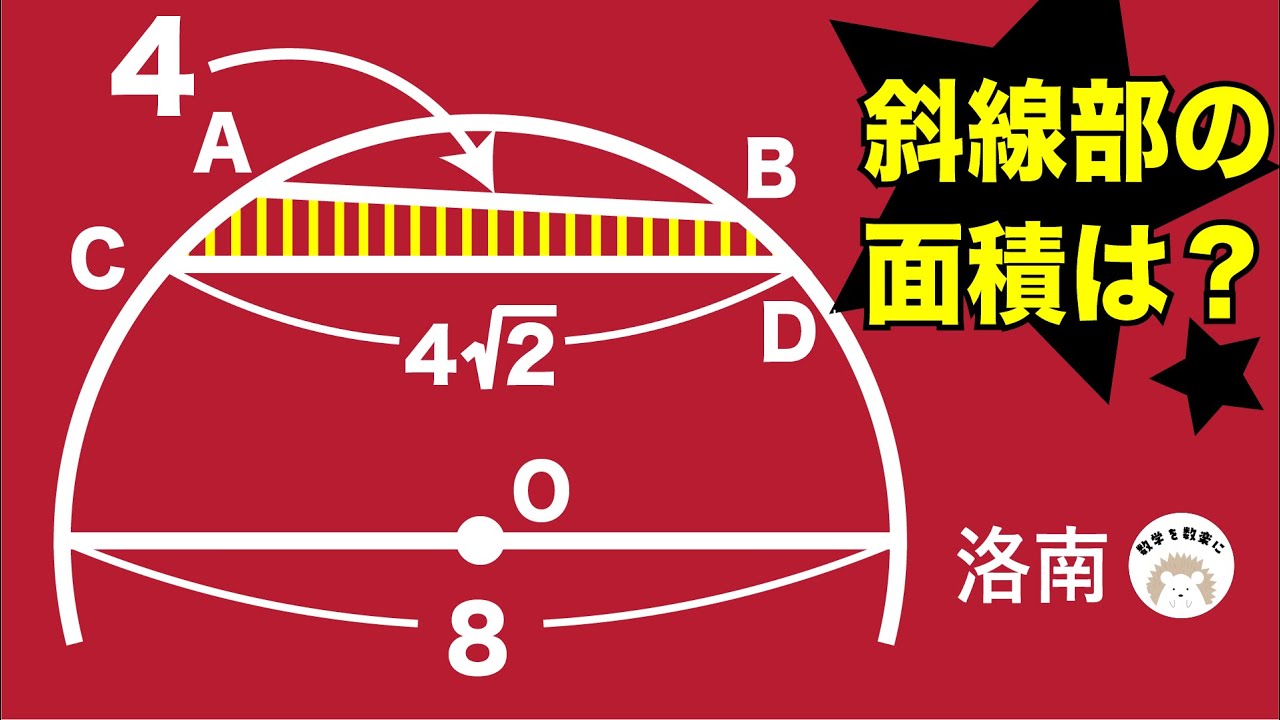
斜線部分の面積を求めよ 洛南高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積を求めよ。
洛南高等学校
この動画を見る
斜線部の面積を求めよ。
洛南高等学校
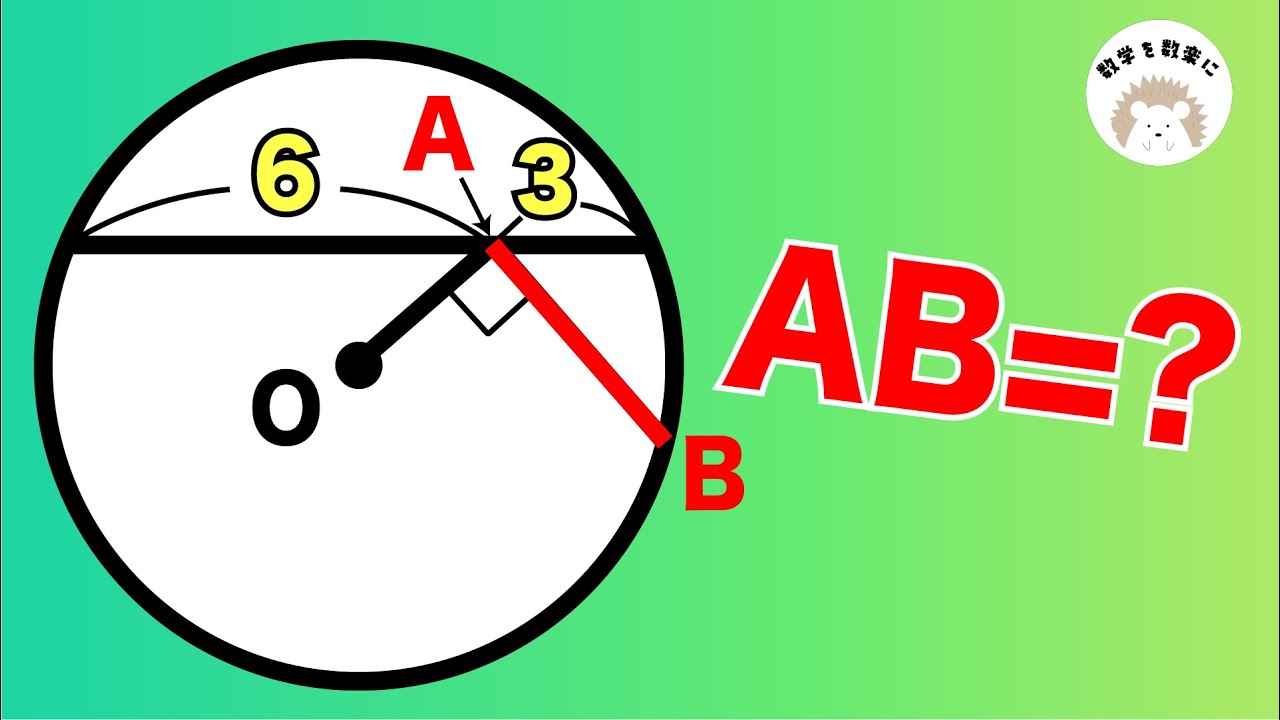
気付けば、そして知っていれば一瞬!!円
福田の1.5倍速演習〜合格する重要問題041〜上智大学2019年度TEAP文系第3問〜長方形の紙を折り返す問題

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上のベクトル#図形と方程式#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$AB=2,BC=3$の長方形ABCDの形の紙がある。DE=aとなる辺DC上の
点Eを考える。AがEと重なるように紙を折るとき、折り目となる線と辺AD,
辺BCとの交点をそれぞれP,Qとする。
(1)aを用いて表すと、$AP=\frac{\boxed{二}}{\boxed{ヌ}}a^2+\frac{\boxed{ネ}}{\boxed{ノ}}$である.
(2)aを用いて表すと、$BQ=\frac{\boxed{ハ}}{\boxed{ヒ}}a^2+
\frac{\boxed{フ}}{\boxed{ヘ}}a+\frac{\boxed{ホ}}{\boxed{マ}}$である。
(3)aを用いて表すと、$PQ=\frac{\boxed{ミ}}{\boxed{ム}}\sqrt{a^2+\boxed{メ}}$である。
(4)四角形ABQPの面積はaを用いて表すと、$\frac{\boxed{モ}}{\boxed{ヤ}}a^2+\frac{\boxed{ユ}}{\boxed{ヨ}}a+\boxed{ラ}$
であり、その最小値は$\frac{\boxed{リ}}{\boxed{ル}}$である。
2019上智大過去問
この動画を見る
$AB=2,BC=3$の長方形ABCDの形の紙がある。DE=aとなる辺DC上の
点Eを考える。AがEと重なるように紙を折るとき、折り目となる線と辺AD,
辺BCとの交点をそれぞれP,Qとする。
(1)aを用いて表すと、$AP=\frac{\boxed{二}}{\boxed{ヌ}}a^2+\frac{\boxed{ネ}}{\boxed{ノ}}$である.
(2)aを用いて表すと、$BQ=\frac{\boxed{ハ}}{\boxed{ヒ}}a^2+
\frac{\boxed{フ}}{\boxed{ヘ}}a+\frac{\boxed{ホ}}{\boxed{マ}}$である。
(3)aを用いて表すと、$PQ=\frac{\boxed{ミ}}{\boxed{ム}}\sqrt{a^2+\boxed{メ}}$である。
(4)四角形ABQPの面積はaを用いて表すと、$\frac{\boxed{モ}}{\boxed{ヤ}}a^2+\frac{\boxed{ユ}}{\boxed{ヨ}}a+\boxed{ラ}$
であり、その最小値は$\frac{\boxed{リ}}{\boxed{ル}}$である。
2019上智大過去問
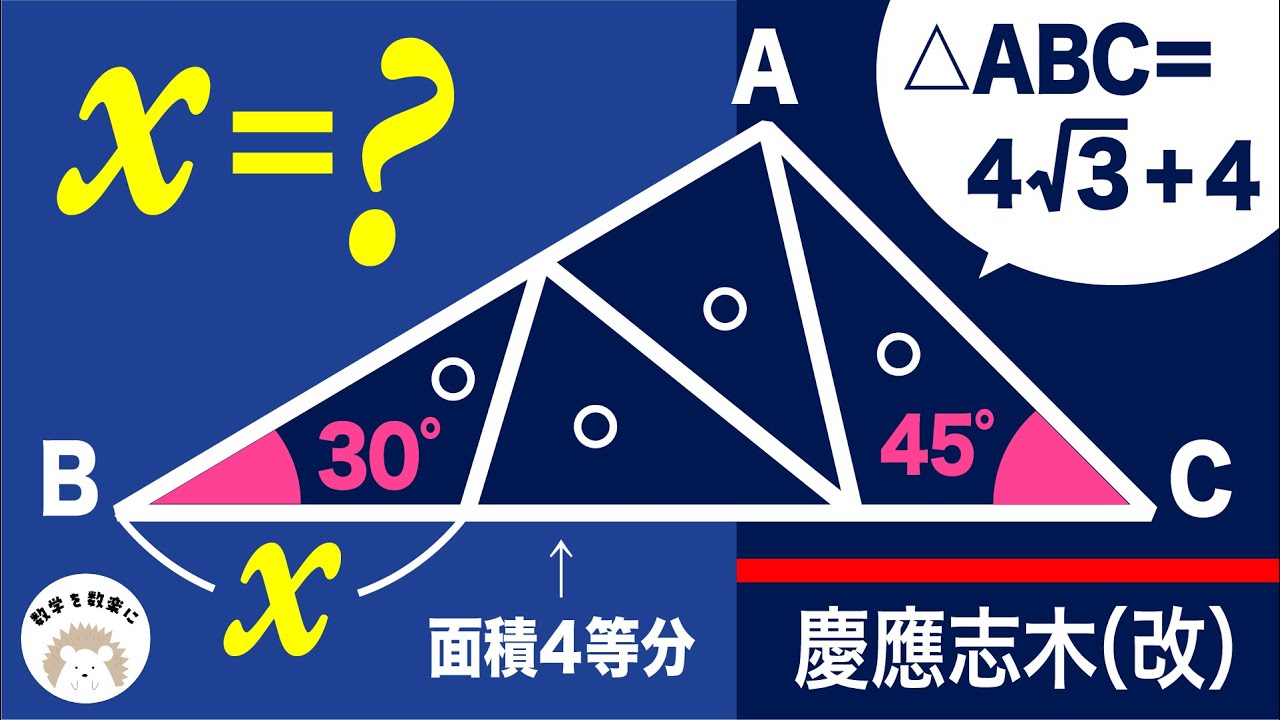
面積比やら三平方の定理やら。。良問!!慶應志木
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
面積4等分
$△ABC=4 \sqrt 3 +4$
x=?
*図は動画内参照
慶應義塾志木高等学校(改)
この動画を見る
面積4等分
$△ABC=4 \sqrt 3 +4$
x=?
*図は動画内参照
慶應義塾志木高等学校(改)
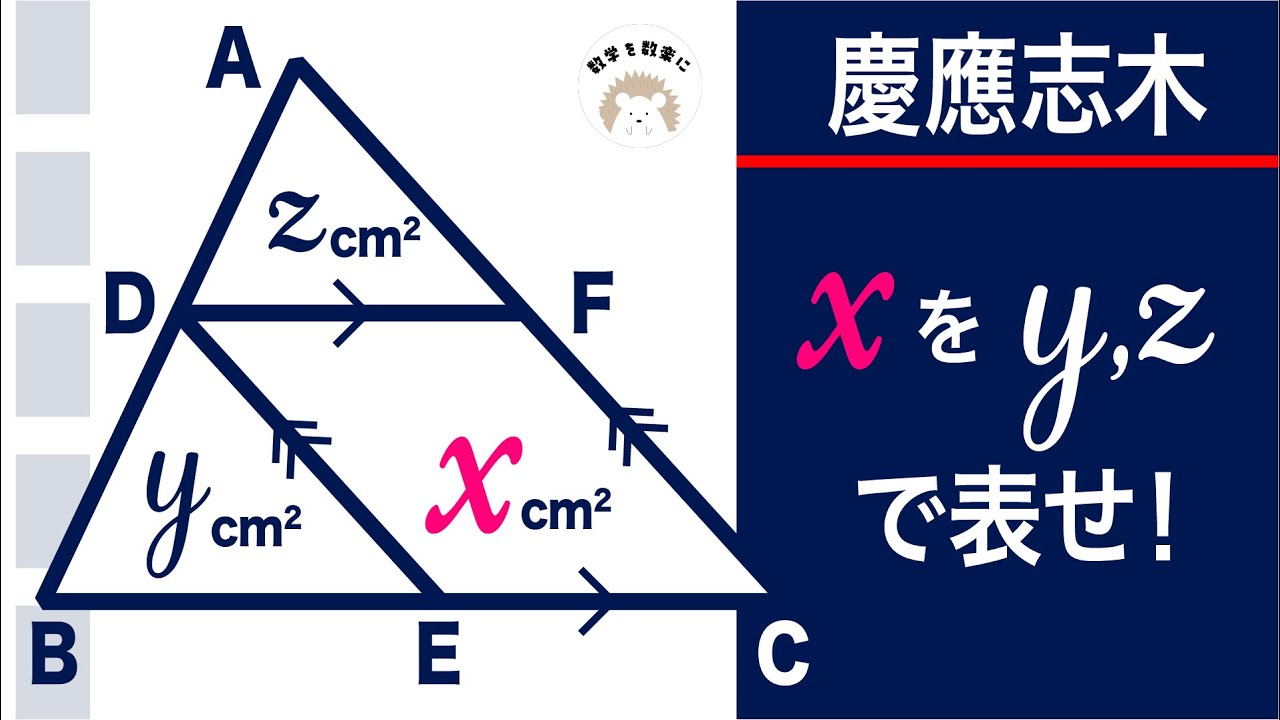
面積から辺への引越し 慶應志木
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xをy,zで表せ
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
xをy,zで表せ
*図は動画内参照
慶應義塾志木高等学校
福田の1.5倍速演習〜合格する重要問題030〜東京大学2016年度文系第1問〜鋭角三角形となる条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上のベクトル#図形と方程式#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の3点$P(x,y), Q(-x,-y), R(1,0)$が鋭角三角形をなすための$(x,y)$
についての条件を求めよ。また、その条件を満たす点P(x,y)の範囲を図示せよ。
2016東京大学文系過去問
この動画を見る
座標平面上の3点$P(x,y), Q(-x,-y), R(1,0)$が鋭角三角形をなすための$(x,y)$
についての条件を求めよ。また、その条件を満たす点P(x,y)の範囲を図示せよ。
2016東京大学文系過去問
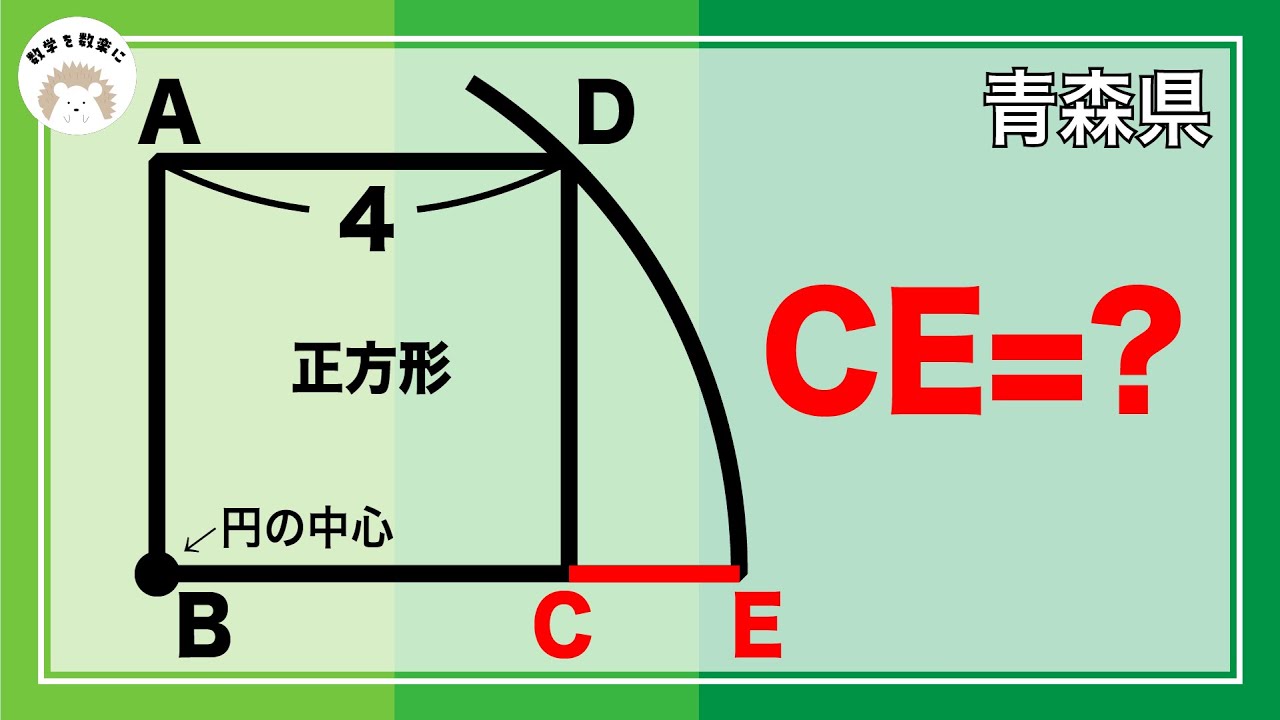
気付けば一瞬!!円と正方形
【保存版】こんな簡単にでるん?
正方形の中にある直角三角形の面積
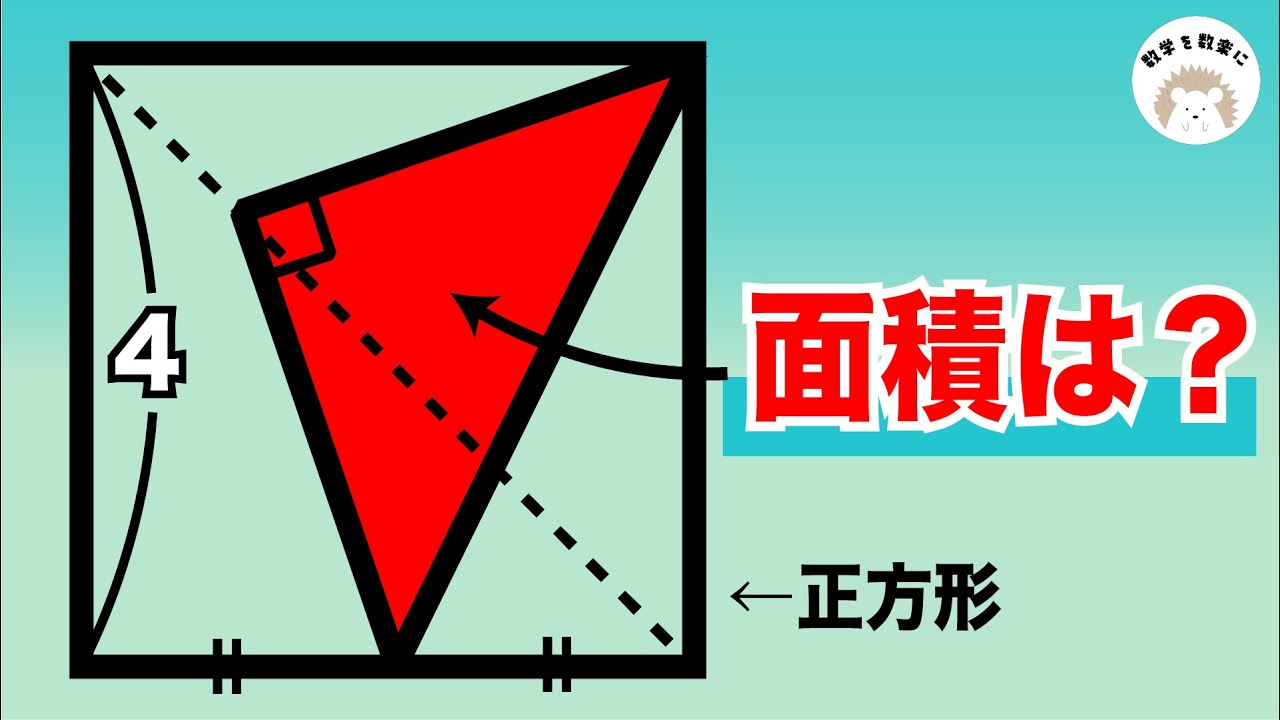
円と長方形
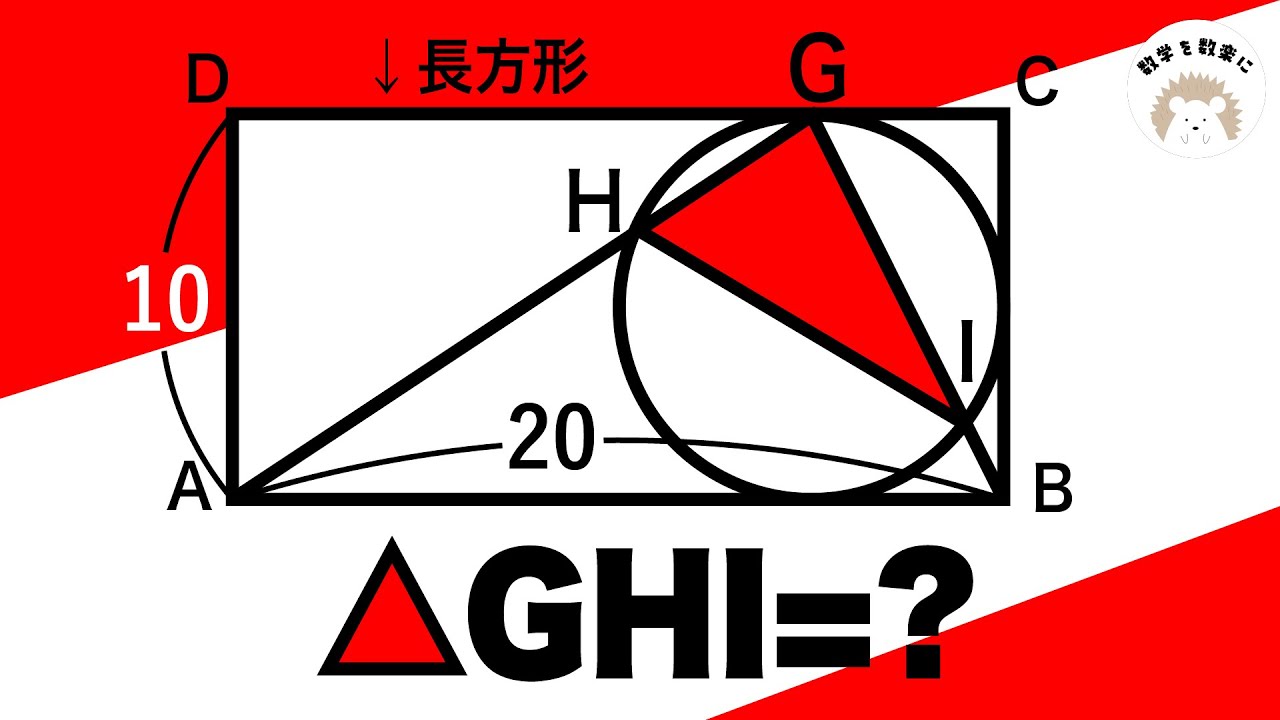
正六角形

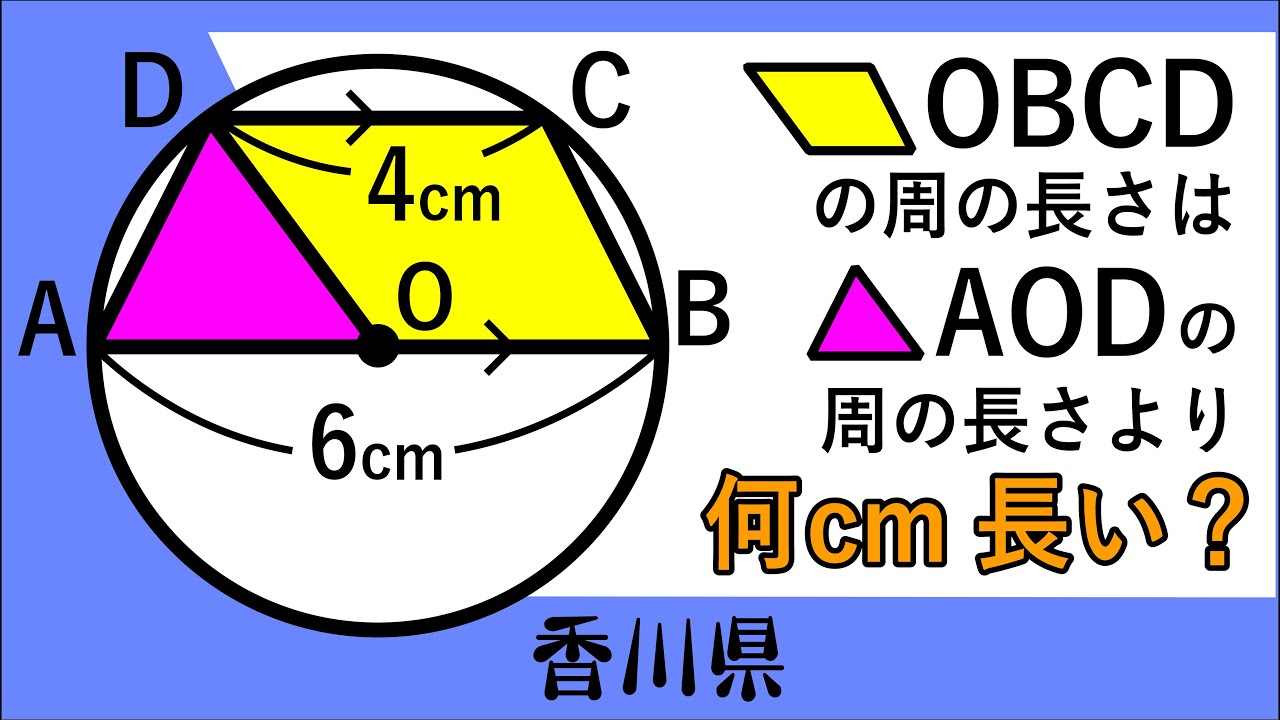
気づけば一瞬!!円に内接する台形 香川県
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形OBCDの周の長さは△AODの周の長さより何㎝長い?
*図は動画内参照
香川県
この動画を見る
四角形OBCDの周の長さは△AODの周の長さより何㎝長い?
*図は動画内参照
香川県
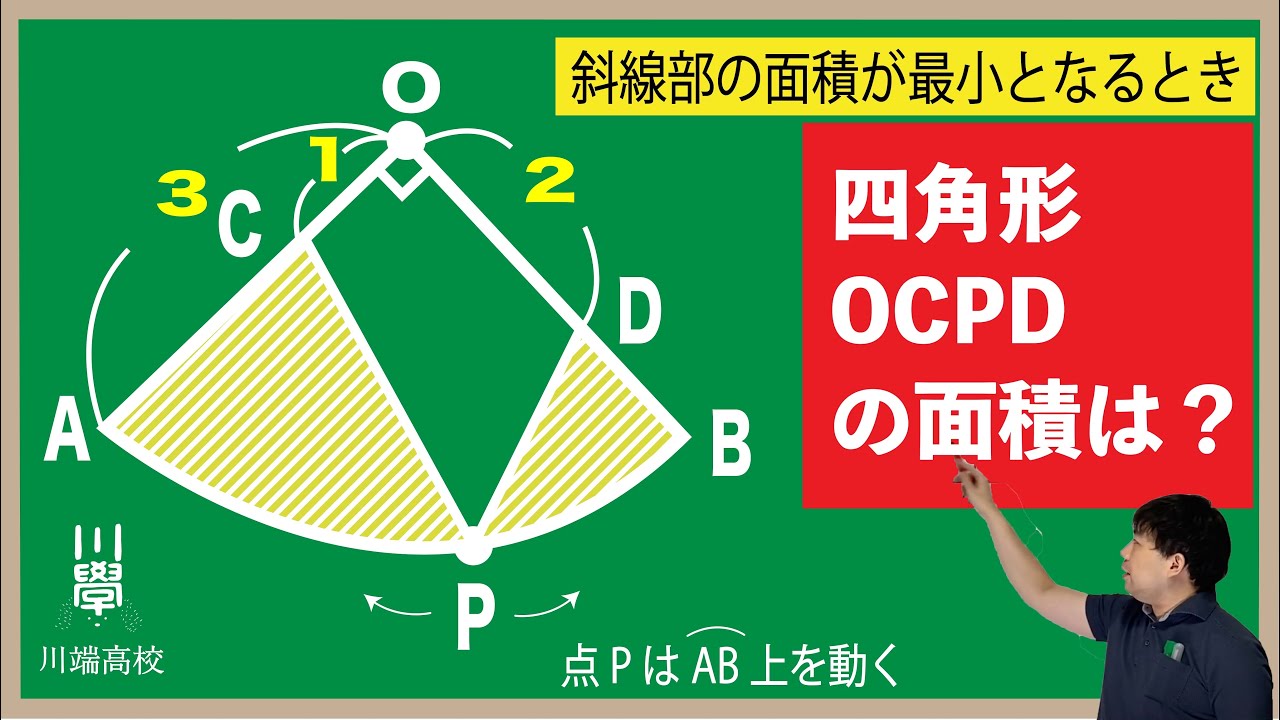
面積が最小となるとき
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Pは$\stackrel{\huge\frown}{AB}$上を動く
斜線部の面積が最小となるとき四角形OCPDの面積は?
*図は動画内参照
川端高校
この動画を見る
点Pは$\stackrel{\huge\frown}{AB}$上を動く
斜線部の面積が最小となるとき四角形OCPDの面積は?
*図は動画内参照
川端高校
見た目は難問!?直角三角形に関する問題
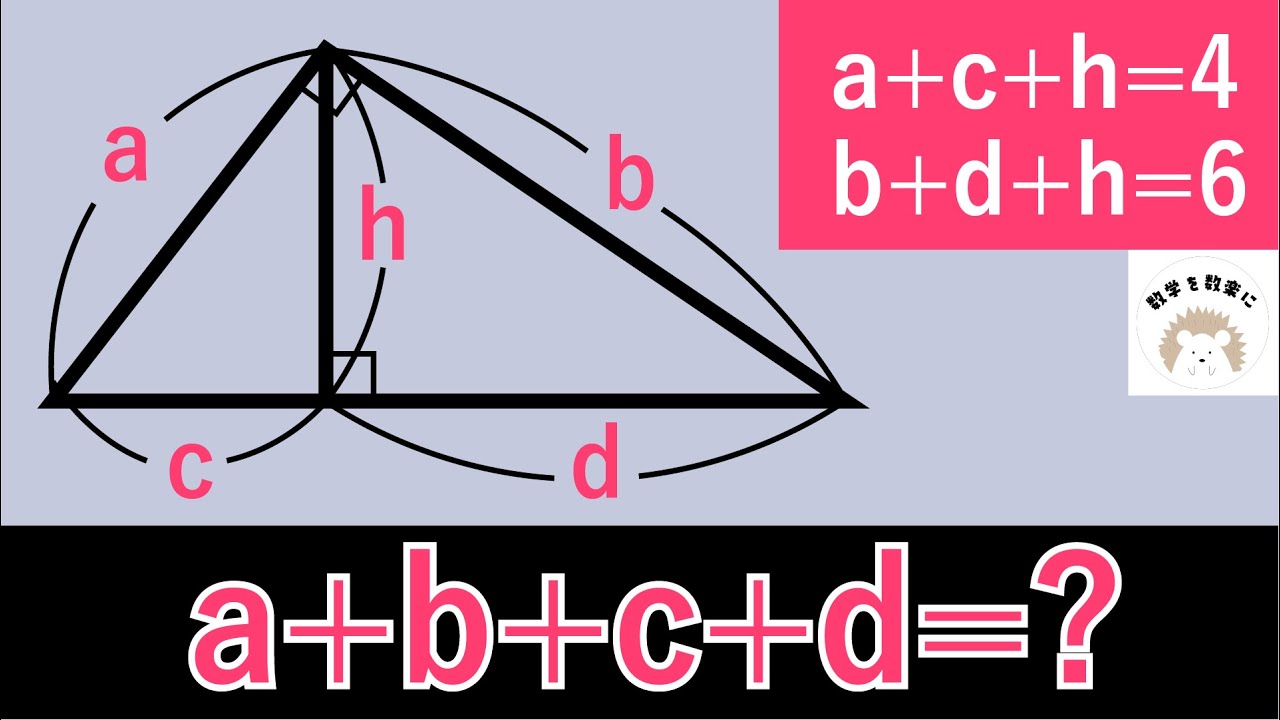
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a+c+h = 4
b+d+h = 6
a+b+c+d =?
*図は動画内参照
この動画を見る
a+c+h = 4
b+d+h = 6
a+b+c+d =?
*図は動画内参照
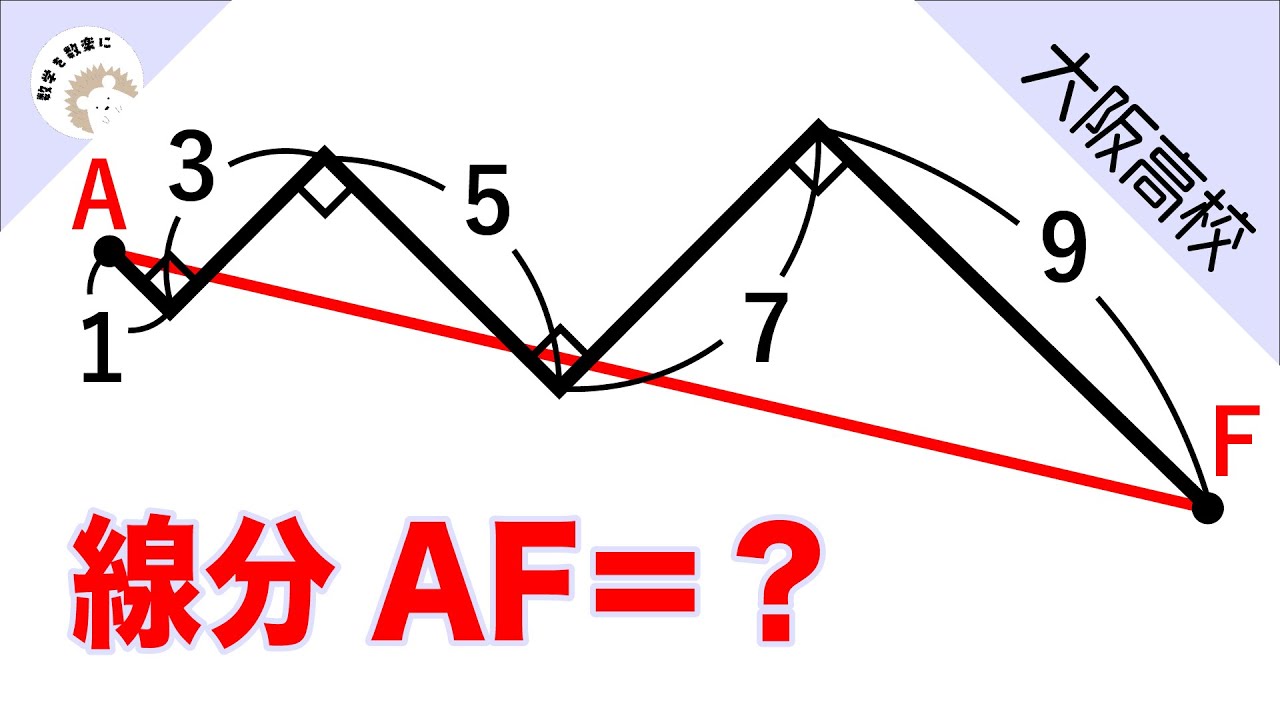
ジグザグ 大阪高校
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
線分AF=?
*図は動画内参照
大阪高等学校
この動画を見る
線分AF=?
*図は動画内参照
大阪高等学校
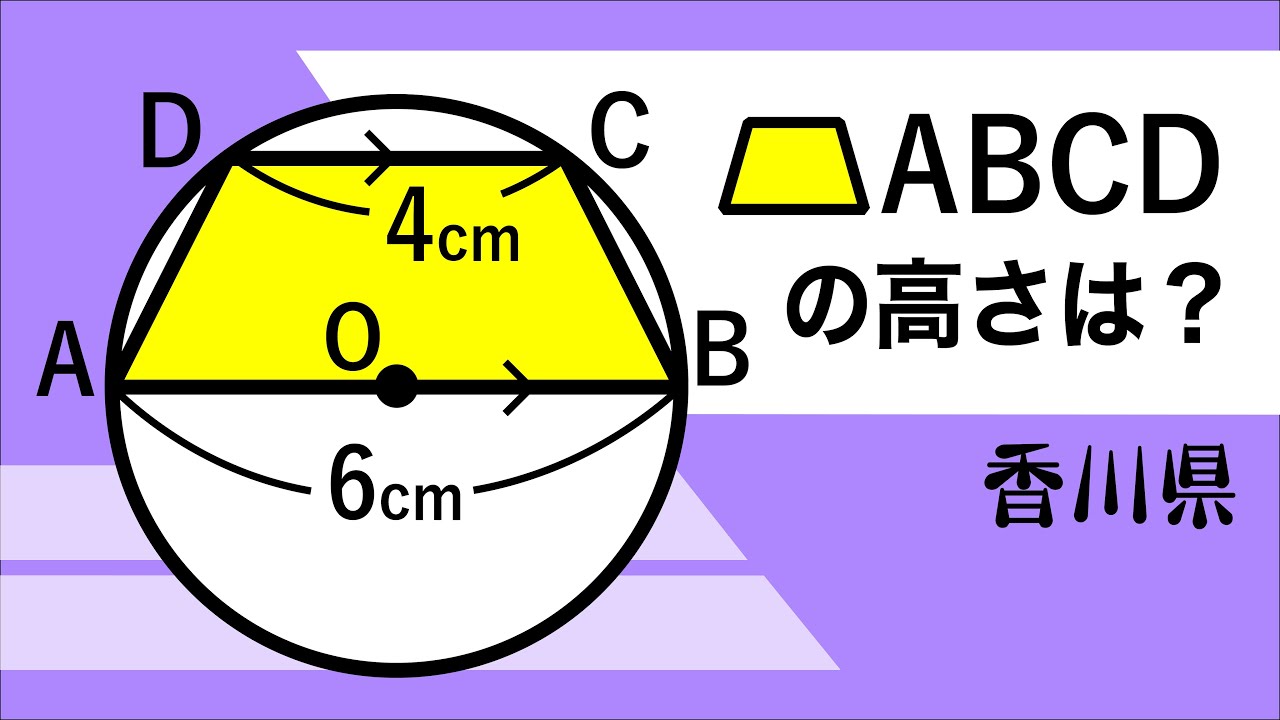
円と台形
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
台形ABCDの高さは?
*図は動画内参照
香川県
この動画を見る
台形ABCDの高さは?
*図は動画内参照
香川県
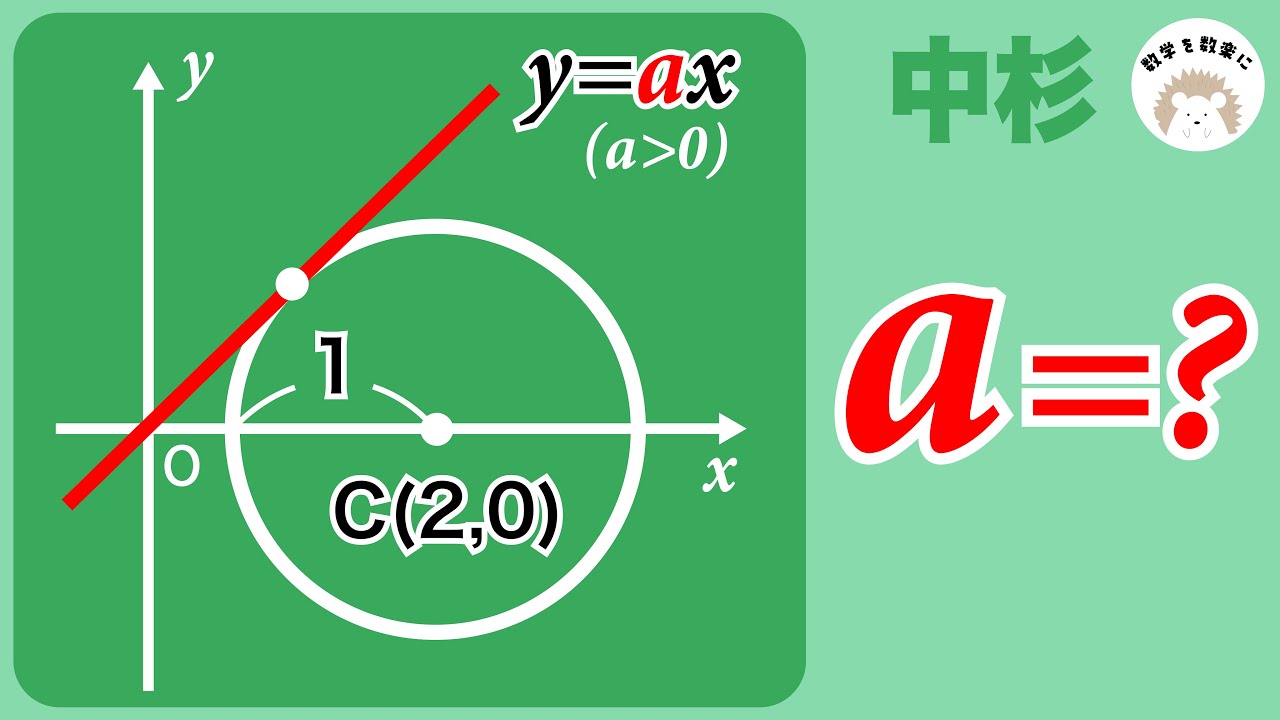
座標平面 円と接線 中央大杉並
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
y=ax
a=?
*図は動画内参照
中央大学杉並高等学校
この動画を見る
y=ax
a=?
*図は動画内参照
中央大学杉並高等学校
【数B】ベクトル:ベクトルの基本⑭係数比較、メネラウスの定理でベクトルを求める

単元:
#数A#図形の性質#平面上のベクトル#内心・外心・重心とチェバ・メネラウス#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ.
この動画を見る
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ.
長方形と円 愛知県

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形ABCDの面積=?
*図は動画内参照
愛知県
この動画を見る
長方形ABCDの面積=?
*図は動画内参照
愛知県
