約数・倍数・整数の割り算と余り・合同式
約数・倍数・整数の割り算と余り・合同式
整数の良問だよ！やや難？
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b,c$は非負整数である.
$a!+5^b=7^c$を満たす$(a,b,c)$をすべて求めよ.
この動画を見る
$a,b,c$は非負整数である.
$a!+5^b=7^c$を満たす$(a,b,c)$をすべて求めよ.
整数の良問だよ！やや難？
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
a,b,cは非負整数である.
$ a!+5^b=7^c $を満たす(a,b,c)をすべて求めよ.
この動画を見る
a,b,cは非負整数である.
$ a!+5^b=7^c $を満たす(a,b,c)をすべて求めよ.
素数に関する整数問題
単元：
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x^3+5$が素数となる素数xは何コ？
京都教育大学附属高等学校
この動画を見る
$x^3+5$が素数となる素数xは何コ？
京都教育大学附属高等学校
福田の数学〜名古屋大学2022年理系第１問〜割り算の余りと異なる実数解の個数
単元：
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{1}}\ a,bを実数とする。 \\
(1)整式x^3を2次式(x-a)^2で割った時の余りを求めよ。 \ \ \\
(2)実数を係数とする2次式f(x)=x^2+\alpha x+\betaで整式x^3を割った時の余りが\\
3x+bとする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
\end{eqnarray}
2022名古屋大学理系過去問
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}}\ a,bを実数とする。 \\
(1)整式x^3を2次式(x-a)^2で割った時の余りを求めよ。 \ \ \\
(2)実数を係数とする2次式f(x)=x^2+\alpha x+\betaで整式x^3を割った時の余りが\\
3x+bとする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
\end{eqnarray}
2022名古屋大学理系過去問
【足元をすくわれるな！】整数：八代白百合学園高等学校～全国入試問題解法
単元：
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
次の問いに答えなさい.
$-2.7$より大きく$\dfrac{14}{3}$より小さい整数は全部で何個あるか.
八代白百合学園高等学校過去問
この動画を見る
次の問いに答えなさい.
$-2.7$より大きく$\dfrac{14}{3}$より小さい整数は全部で何個あるか.
八代白百合学園高等学校過去問
解けるように作られた問題 ガウス少年なら一瞬
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ f(x)=\dfrac{25^x}{25^x+5}$である.
$ f \left(\dfrac{1}{100}\right)+f \left(\dfrac{2}{100}\right)+
･･････+f \left(\dfrac{98}{100}\right)+\left(\dfrac{99}{100}\right)$の値を求めよ.
この動画を見る
$ f(x)=\dfrac{25^x}{25^x+5}$である.
$ f \left(\dfrac{1}{100}\right)+f \left(\dfrac{2}{100}\right)+
･･････+f \left(\dfrac{98}{100}\right)+\left(\dfrac{99}{100}\right)$の値を求めよ.
【考え方が理解で得意になる！！】合同式がこの一本でできるようになる！プチ演習付き〔数学、高校数学〕
基本問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
整数$m$をすべて求めよ.
$\dfrac{8^m-2^m}{6^m-3^m}=2$
この動画を見る
整数$m$をすべて求めよ.
$\dfrac{8^m-2^m}{6^m-3^m}=2$
ちょっと難しいか…？
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
32,7,105,98,64,606,73
この中から2つの整数を選ぶとその差が必ず6で割り切れるものがあることを説明せよ
この動画を見る
32,7,105,98,64,606,73
この中から2つの整数を選ぶとその差が必ず6で割り切れるものがあることを説明せよ
ざ・見掛け倒し
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ \displaystyle \sum_{n=1}^{2022} n^{2022}$
$ =1^{2022}+2^{2022}+3^{2022}+･･････$
$+2021^{2022}+2022^{2022}$
を13で割った余りを求めよ.
この動画を見る
$ \displaystyle \sum_{n=1}^{2022} n^{2022}$
$ =1^{2022}+2^{2022}+3^{2022}+･･････$
$+2021^{2022}+2022^{2022}$
を13で割った余りを求めよ.
Q：鳩の巣原理の解説して下さい
素数
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n^4-11n^2+49$が素数となる整数$n$を求めよ.
この動画を見る
$n^4-11n^2+49$が素数となる整数$n$を求めよ.
整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
自然数$ m,n(m \gt n)$を求めよ.
$ \dfrac{1}{m}+\dfrac{1}{n}=\dfrac{3}{77}$
この動画を見る
自然数$ m,n(m \gt n)$を求めよ.
$ \dfrac{1}{m}+\dfrac{1}{n}=\dfrac{3}{77}$
素数判定
整数問題 一橋大 令和四年
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$2^a3^b+2^c3^d = 2022$を満たす0以上の整数a,b,c,dの組を求めよ。
2022一橋大学
この動画を見る
$2^a3^b+2^c3^d = 2022$を満たす0以上の整数a,b,c,dの組を求めよ。
2022一橋大学
雑問
単元：
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
この動画を見る
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
明治学院 令和4年度 2022 入試問題100題解説85問目！
単元：
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
a,bは整数とする。
$ab^2+2ab+a=50$
a+bの最小値は？
2022明治学院高等学校
この動画を見る
a,bは整数とする。
$ab^2+2ab+a=50$
a+bの最小値は？
2022明治学院高等学校
ニャンニャン問題2022
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 222.......22$のようにすべての桁の数が$2$である整数の中には
必ず$2022$の倍数があることを示せ.
この動画を見る
$ 222.......22$のようにすべての桁の数が$2$である整数の中には
必ず$2022$の倍数があることを示せ.
【糸口を探せ！】整数：同志社国際高等学校～全国入試問題解法
単元：
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\sqrt{24n}$と$\sqrt{n+27}$がともに整数になるような最小の自然数$n$の値を求めよ.
同志社国際高校過去問
この動画を見る
$\sqrt{24n}$と$\sqrt{n+27}$がともに整数になるような最小の自然数$n$の値を求めよ.
同志社国際高校過去問
無題
単元：
#数Ⅰ#数A#数と式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ n^2-331n-2022$が$101$の倍数となる
$ 2$桁の自然数$ n$を$1$つ見つけよ.
この動画を見る
$ n^2-331n-2022$が$101$の倍数となる
$ 2$桁の自然数$ n$を$1$つ見つけよ.
一橋大学2022整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 2^a3^b+2^c3^d=2022$を満たす$0$以上の整数$(a,b,c,d)$を求めよ.
2022一橋大過去問
この動画を見る
$ 2^a3^b+2^c3^d=2022$を満たす$0$以上の整数$(a,b,c,d)$を求めよ.
2022一橋大過去問
福田の入試問題解説〜東京大学2022年理系第２問〜約数と倍数と最大公約数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{2}}\ 数列\left\{a_n\right\}を次のように定める。\\
a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)\\
(1)正の整数nが3の倍数のとき、a_nは5の倍数となることを示せ。\\
(2)k,nを正の整数とする。a_nがa_kの倍数となるための必要十分条件をk,nを\\
用いて表せ。\\
(3)a_{2022}と(a_{8091})^2の最大公約数を求めよ。
\end{eqnarray}
2022東京大学理系過去問
この動画を見る
\begin{eqnarray}
{\Large\boxed{2}}\ 数列\left\{a_n\right\}を次のように定める。\\
a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)\\
(1)正の整数nが3の倍数のとき、a_nは5の倍数となることを示せ。\\
(2)k,nを正の整数とする。a_nがa_kの倍数となるための必要十分条件をk,nを\\
用いて表せ。\\
(3)a_{2022}と(a_{8091})^2の最大公約数を求めよ。
\end{eqnarray}
2022東京大学理系過去問
ざ・見掛け倒しだよ
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ \dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+……+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を$17$で割った余りを求めよ.
この動画を見る
$ \dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+……+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を$17$で割った余りを求めよ.
福田の数学〜東京慈恵会医科大学2022年医学部第３問〜約数と倍数の性質
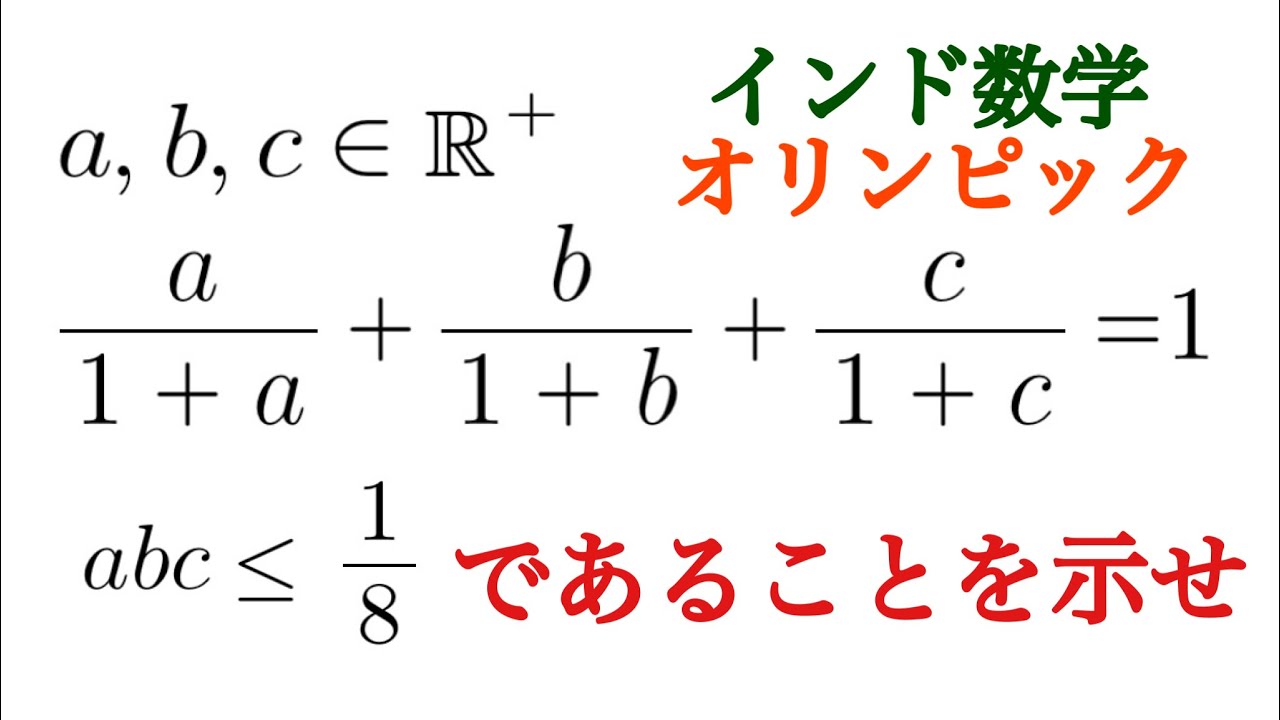
単元：
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{3}}\ mは3以上の奇数とし、mの全ての正の約数をa_1,a_2,\ldots,a_kと並べる。\\
ただし、a_1 \lt a_2 \lt \ldots \lt a_kとする。\\
以下の2つの条件(\textrm{i}),(\textrm{ii})を満たすmについて考える。\\
(\textrm{i})mは素数ではない。\\
(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt kを満たす全ての整数i,jについてa_j-a_i \leqq 3が\\
成り立つ。\\
このとき、次の問いに答えよ。\\
(1)kは3または4であることを示し、mをa_2を用いて表せ。\\
(2)k=3となるとき、全ての正の整数nについて(a_2n+1)^{a_2}-1は\\
mの倍数であることを示せ。
\end{eqnarray}
2022東京慈恵会医科大学医学部過去問
この動画を見る
\begin{eqnarray}
{\Large\boxed{3}}\ mは3以上の奇数とし、mの全ての正の約数をa_1,a_2,\ldots,a_kと並べる。\\
ただし、a_1 \lt a_2 \lt \ldots \lt a_kとする。\\
以下の2つの条件(\textrm{i}),(\textrm{ii})を満たすmについて考える。\\
(\textrm{i})mは素数ではない。\\
(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt kを満たす全ての整数i,jについてa_j-a_i \leqq 3が\\
成り立つ。\\
このとき、次の問いに答えよ。\\
(1)kは3または4であることを示し、mをa_2を用いて表せ。\\
(2)k=3となるとき、全ての正の整数nについて(a_2n+1)^{a_2}-1は\\
mの倍数であることを示せ。
\end{eqnarray}
2022東京慈恵会医科大学医学部過去問
2022都立入試 整数問題証明(11の倍数)
単元：
#数学(中学生)#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数列#数列とその和（等差・等比・階差・Σ）#高校入試過去問(数学)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022都立入試 整数問題証明に関して解説していきます.
この動画を見る
2022都立入試 整数問題証明に関して解説していきます.
【題意をつかもう！数学の意味を知ろう！】整数：沖縄県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
「ある2桁の自然数$X$と,その数の十の位の数と一の位の数を入れ替えてできる数$Y$との和が$132$になる.」
もとの自然数$X$として考えられる数をすべて求めなさい.
※もとの自然数$X$は,十の位の数が一の位の数より大きいものとする.
沖縄県高校過去問
この動画を見る
「ある2桁の自然数$X$と,その数の十の位の数と一の位の数を入れ替えてできる数$Y$との和が$132$になる.」
もとの自然数$X$として考えられる数をすべて求めなさい.
※もとの自然数$X$は,十の位の数が一の位の数より大きいものとする.
沖縄県高校過去問
整数問題 須磨学園（改） 2022年入試問題100問解説の53問目
単元：
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x^2+6xy+10y^2+6y=9$を満たす整数の組（x,y）をすべて求めよ。
2022須磨学園高等学校
この動画を見る
$x^2+6xy+10y^2+6y=9$を満たす整数の組（x,y）をすべて求めよ。
2022須磨学園高等学校
2022年の整数問題！この問題好きです❤️ 早稲田大学高等学院2022年入試問題解説49問目
単元：
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$2022=x \sqrt y (x^y+y^y)$
を満たす自然数x,yは？
2022早稲田大学高等学院
この動画を見る
$2022=x \sqrt y (x^y+y^y)$
を満たす自然数x,yは？
2022早稲田大学高等学院
整数問題 慶應志木高校2022入試問題解説36問目
単元：
#数学(中学生)#数Ⅰ#数A#２次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
xについての2次方程式
$x^2-(4t-1)x+4t^2-2t = 0$の2つの解をα、βとする
5,α,βを辺にもつ三角形が直角三角形のとき
tの値は？
2022慶應義塾志木高等学校
この動画を見る
xについての2次方程式
$x^2-(4t-1)x+4t^2-2t = 0$の2つの解をα、βとする
5,α,βを辺にもつ三角形が直角三角形のとき
tの値は？
2022慶應義塾志木高等学校
東京大学 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
n,a,b,c,dは0または正の整数
$
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2+d^2 = n^2 -6 \\
a+b+c+d = n \\
a \geqq b \geqq c \geqq d
\end{array}
\right.
\end{eqnarray}
$
を満たす(n,a,b,c,d)数の組を全て求めよ
1980年代東京大学
この動画を見る
n,a,b,c,dは0または正の整数
$
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2+d^2 = n^2 -6 \\
a+b+c+d = n \\
a \geqq b \geqq c \geqq d
\end{array}
\right.
\end{eqnarray}
$
を満たす(n,a,b,c,d)数の組を全て求めよ
1980年代東京大学