 整数の性質
整数の性質
 整数の性質
整数の性質
数1

中学生向け整数問題

単元:
#数A#整数の性質#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数(x,y,z)をすべて求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy+xz=255 \\
xz-yz-224
\end{array}
\right.
\end{eqnarray}$
この動画を見る
自然数(x,y,z)をすべて求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy+xz=255 \\
xz-yz-224
\end{array}
\right.
\end{eqnarray}$
【数学】東京海洋大2021年度整数問題(2)解説

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京海洋大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(2)pが5以上の素数であるとき、$p^2-1$は6の倍数であることを示せ
この動画を見る
(2)pが5以上の素数であるとき、$p^2-1$は6の倍数であることを示せ
高校入試だけどもガウス記号 大阪星光学院

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
記号[x]はxを超えない最大の整数。
$[(\frac{x-1}{2})^2] = \frac{x}{2} + 3 $のときx=?
大阪星光学院高等学校
この動画を見る
記号[x]はxを超えない最大の整数。
$[(\frac{x-1}{2})^2] = \frac{x}{2} + 3 $のときx=?
大阪星光学院高等学校
整数問題 基本
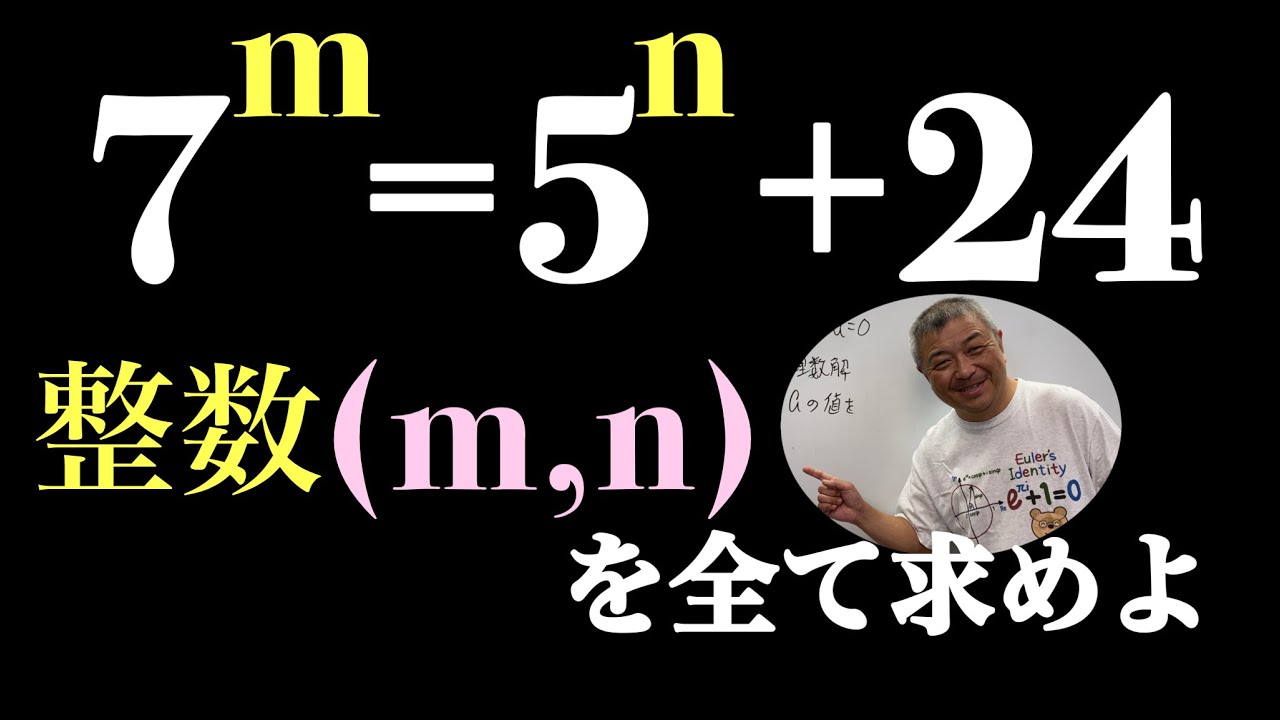
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$7^m=5^n+24$を満たす整数(m,n)を求めよ.
この動画を見る
$7^m=5^n+24$を満たす整数(m,n)を求めよ.
福田の1.5倍速演習〜合格する重要問題028〜九州大学2016年度文理共通問題〜余りと合同式

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#茨城大学
指導講師:
福田次郎
問題文全文(内容文):
自然数nに対して、$10^n$を13で割った余りを$a_n$とおく。$a_n$は0から12まで
の整数である。以下の問いに答えよ。
(1)$a_{n+1}$は$10a_n$を13で割った余りに等しいことを示せ。
(2)$a_1,a_2,a_3,\cdots,a_6$を求めよ。
(3)以下の3条件を満たす自然数Nをすべて求めよ。
$(\textrm{i})N$を十進法で表示した時6桁となる。
$(\textrm{ii})N$を十進法で表示して、最初と最後の桁の数字を取り除くと
2016となる。
$(\textrm{iii})N$は13で割り切れる。
2016九州大学文理過去問
この動画を見る
自然数nに対して、$10^n$を13で割った余りを$a_n$とおく。$a_n$は0から12まで
の整数である。以下の問いに答えよ。
(1)$a_{n+1}$は$10a_n$を13で割った余りに等しいことを示せ。
(2)$a_1,a_2,a_3,\cdots,a_6$を求めよ。
(3)以下の3条件を満たす自然数Nをすべて求めよ。
$(\textrm{i})N$を十進法で表示した時6桁となる。
$(\textrm{ii})N$を十進法で表示して、最初と最後の桁の数字を取り除くと
2016となる。
$(\textrm{iii})N$は13で割り切れる。
2016九州大学文理過去問
素数問題

早稲田高等学院 高校入試に九九!?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
九九の表の81個の数の積を素因数分解せよ.
早稲田高等学院過去問
この動画を見る
九九の表の81個の数の積を素因数分解せよ.
早稲田高等学院過去問
福田の1.5倍速演習〜合格する重要問題019〜東京工業大学2016年度理系数学第4問〜整数に関する論証

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを2以上の自然数とする。
(1)nが素数または4のとき、$(n-1)!$はnで割り切れないことを示せ。
(2)nが素数でなくかつ4でもないとき、$(n-1)!$はnで割り切れることを示せ。
2016東京工業大学理系過去問
この動画を見る
nを2以上の自然数とする。
(1)nが素数または4のとき、$(n-1)!$はnで割り切れないことを示せ。
(2)nが素数でなくかつ4でもないとき、$(n-1)!$はnで割り切れることを示せ。
2016東京工業大学理系過去問
福田の1.5倍速演習〜合格する重要問題018〜東北大学2016年度文系数学第3問〜3変数の不定方程式

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある工場で作る部品A,B,Cはねじをそれぞれ7個、9個、12個使っている。
出荷後に残ったこれらの部品のねじを全て外したところ、ネジが全部で54個あった。
残った部品A,B,Cの個数をそれぞれl,m,nとして可能性のある組(l,m,n)を全て求めよ。
2016東北大学文系過去問
この動画を見る
ある工場で作る部品A,B,Cはねじをそれぞれ7個、9個、12個使っている。
出荷後に残ったこれらの部品のねじを全て外したところ、ネジが全部で54個あった。
残った部品A,B,Cの個数をそれぞれl,m,nとして可能性のある組(l,m,n)を全て求めよ。
2016東北大学文系過去問
高校入試にしては頑張った出題 愛光学園

単元:
#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{180-3n}$が整数となる最小の①自然数n②正の有理数nを求めよ.
愛光学園過去問
この動画を見る
$\sqrt{180-3n}$が整数となる最小の①自然数n②正の有理数nを求めよ.
愛光学園過去問
福田の1.5倍速演習〜合格する重要問題016〜京都大学2016年度理系数学第2問〜素数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学的帰納法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
この動画を見る
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
合同式(mod)について6分で説明します【数学A】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
合同式(mod)について6分で説明します
この動画を見る
合同式(mod)について6分で説明します
福田の1.5倍速演習〜合格する重要問題011〜東京大学2015年度理系数学第5問〜コンビネーションの性質

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
mを2015以下の正の整数とする。
2015Cmが偶数となる最小のmを求めよ
2015東京大学理系過去問
この動画を見る
mを2015以下の正の整数とする。
2015Cmが偶数となる最小のmを求めよ
2015東京大学理系過去問
数学オリンピック日本予選 合同式の基本
単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1111^{2018}$を$11111$で割ったあまりを求めよ.
数学オリンピック過去問
この動画を見る
$1111^{2018}$を$11111$で割ったあまりを求めよ.
数学オリンピック過去問
階乗の入った方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n!=n^2+11n+40$を満たす自然数nを求めよ.
この動画を見る
$n!=n^2+11n+40$を満たす自然数nを求めよ.
福田の1.5倍速演習〜合格する重要問題005〜一橋大学2015年文系数学第1問〜互いに素な自然数の個数

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを2以上の整数とする。n以下の正の整数のうち、nとの最大公約数が1と
なるものの個数をE(n)で表す。たとえば
$E(2)=1,E(3)=2,E(4)=2,...,E(10)=4, ...$
である。
(1)E(1024)を求めよ。
(2)E(2015)を求めよ。
(3)mを正の整数とし、pとqを異なる素数とする。$n=p^mq^mのとき\frac{E(n)}{n}\geqq\frac{1}{3}$
が成り立つことを示せ。
2015一橋大学文系過去問
この動画を見る
nを2以上の整数とする。n以下の正の整数のうち、nとの最大公約数が1と
なるものの個数をE(n)で表す。たとえば
$E(2)=1,E(3)=2,E(4)=2,...,E(10)=4, ...$
である。
(1)E(1024)を求めよ。
(2)E(2015)を求めよ。
(3)mを正の整数とし、pとqを異なる素数とする。$n=p^mq^mのとき\frac{E(n)}{n}\geqq\frac{1}{3}$
が成り立つことを示せ。
2015一橋大学文系過去問
素数に関する問題 国学院高校
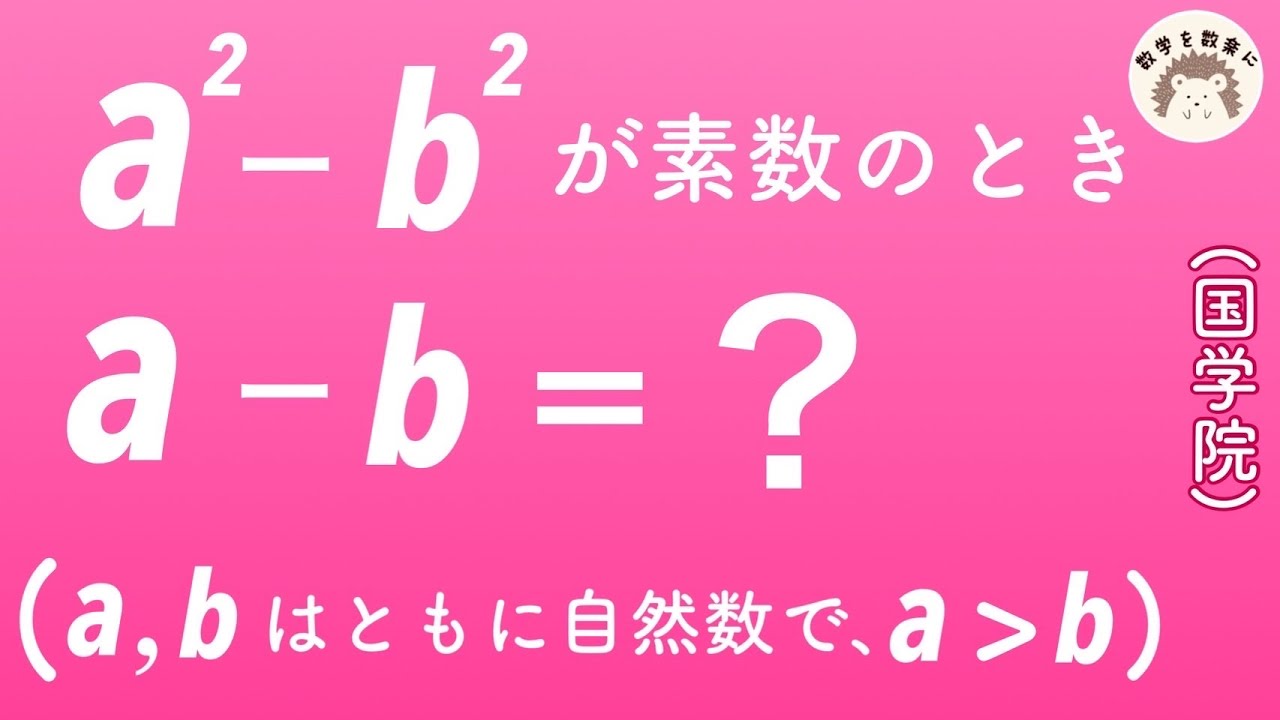
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2-b^2$が素数のとき
a-b=?
(a,bはともに自然数で、a>b)
國學院高等学校
この動画を見る
$a^2-b^2$が素数のとき
a-b=?
(a,bはともに自然数で、a>b)
國學院高等学校
【ひとまず解答してみよう…!】整数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの自然数$m,n$は$2^m-1=(2n+1)(2n+3)$を満たす.
$m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
この動画を見る
2つの自然数$m,n$は$2^m-1=(2n+1)(2n+3)$を満たす.
$m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
京大の整数問題!〇〇に注目!【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
二つの奇数$a,b$に対して,$m=11a+b,n=3a+b$とおく。$m,n$がともに平方数であることはないことを証明せよ。
京都大過去問
この動画を見る
二つの奇数$a,b$に対して,$m=11a+b,n=3a+b$とおく。$m,n$がともに平方数であることはないことを証明せよ。
京都大過去問
ナイスな整数問題だよ

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+y^3+3xy=17$をみたす整数x,yの組をすべて求めよ.
この動画を見る
$x^3+y^3+3xy=17$をみたす整数x,yの組をすべて求めよ.
【条件から導き出されることは…!】整数:灘高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#整数の性質#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x$を$x-n+a$と表す.
$ x^2+a^2=8$のとき,$n=\Box,x=\Box$である.
灘高校過去問
この動画を見る
$x$を$x-n+a$と表す.
$ x^2+a^2=8$のとき,$n=\Box,x=\Box$である.
灘高校過去問
福田の数学〜中央大学2022年経済学部第3問〜下一桁が一致する整数と下二桁が一致する整数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の整数xについて、以下の設問に答えよ。
なお、ここでxの下一桁とはxを10で割った余りであり、
xの下二桁とはxを100で割った余りであるとする。
(1)$10 \leqq x \leqq 40$の範囲で、xn下一桁と$x^2$の下一桁が一致するようなxの個数を求めよ。
(2)$10 \leqq x \leqq 99$の範囲で、$x^2$の下一桁と$x^4$の下一桁が一致するxをすべて足した数を
Yとする。整数Yの下一桁を求めよ。
(3)$10 \leqq x \leqq 99$の範囲で、$x^2$の下二桁がxと等しいものをすべて求めよ。
この動画を見る
正の整数xについて、以下の設問に答えよ。
なお、ここでxの下一桁とはxを10で割った余りであり、
xの下二桁とはxを100で割った余りであるとする。
(1)$10 \leqq x \leqq 40$の範囲で、xn下一桁と$x^2$の下一桁が一致するようなxの個数を求めよ。
(2)$10 \leqq x \leqq 99$の範囲で、$x^2$の下一桁と$x^4$の下一桁が一致するxをすべて足した数を
Yとする。整数Yの下一桁を求めよ。
(3)$10 \leqq x \leqq 99$の範囲で、$x^2$の下二桁がxと等しいものをすべて求めよ。
約数4個の数 渋谷教育学園幕張

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数nはちょうど4つの約数を持ちそのうち2つは素数である。
これら4つの約数の和が24であるような自然数nをすべて求めよ。
渋谷教育学園幕張高等学校
この動画を見る
自然数nはちょうど4つの約数を持ちそのうち2つは素数である。
これら4つの約数の和が24であるような自然数nをすべて求めよ。
渋谷教育学園幕張高等学校
n進法の理解が深まる問題!2通りで解説!【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
10進法で表された数6.75を二進法で表せ。また,この数と2進法で表された数101.0101の積として与えられる数を2進法および4進法で表せ。
この動画を見る
10進法で表された数6.75を二進法で表せ。また,この数と2進法で表された数101.0101の積として与えられる数を2進法および4進法で表せ。
素数を求めよ お茶の水女子大付属

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
123123のように3ケタの同じ整数を2つ並べて6ケタの整数を作るとある素数で必ず割り切れる。
この素数をすべて求めよ。
お茶の水女子大学附属高等学校
この動画を見る
123123のように3ケタの同じ整数を2つ並べて6ケタの整数を作るとある素数で必ず割り切れる。
この素数をすべて求めよ。
お茶の水女子大学附属高等学校
【整数問題】難関大が好きなパターン!範囲を絞り込め!

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$abcd=a+b+c+d$を満たす正の整数$a,b,c,d$をすべて求めよ。
この動画を見る
$abcd=a+b+c+d$を満たす正の整数$a,b,c,d$をすべて求めよ。
割って余る整数問題 慶應女子

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
724を正の整数nで割ると9余り、n+1で割ると4余る。
考えられるnの値をすべて求めよ。
慶應義塾女子高等学校
この動画を見る
724を正の整数nで割ると9余り、n+1で割ると4余る。
考えられるnの値をすべて求めよ。
慶應義塾女子高等学校
【整数問題】難関大が好きなパターン!範囲を絞り込め!

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
abcd=a+b+c+dを満たす正の整数a,b,c,dを求めよ
この動画を見る
abcd=a+b+c+dを満たす正の整数a,b,c,dを求めよ
福田の数学〜中央大学2022年経済学部第1問(1)〜n進数の変換

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)3進法で表された$2022_{(3)}$を8進法で表せ。
2022中央大学経済学部過去問
この動画を見る
(1)3進法で表された$2022_{(3)}$を8進法で表せ。
2022中央大学経済学部過去問
