 整数の性質
整数の性質
 整数の性質
整数の性質
一次不定方程式の不可能解の最大値の証明

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,bは互いに素な自然数である.x,yは0以上の整数であり,$ax+by$で表せない.
最大の整数はab-a-bであることを示せ.
この動画を見る
a,bは互いに素な自然数である.x,yは0以上の整数であり,$ax+by$で表せない.
最大の整数はab-a-bであることを示せ.
一次不定方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 48以上の整数は0以上の整数x,yを用いて$7x+9y$で表せることを示せ.
この動画を見る
$ 48以上の整数は0以上の整数x,yを用いて$7x+9y$で表せることを示せ.
東海大(医)えっ!そんなんでいいの?

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$n^3+100$が$n+10$で割り切れるような最大の自然数$n$を求めよ.
東海大(医)過去問
この動画を見る
自然数$n^3+100$が$n+10$で割り切れるような最大の自然数$n$を求めよ.
東海大(医)過去問
東海大(医)えっ!そんなんでいいの?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$n^3+100$が$n+10$で割り切れるような最大の自然数nを求めよ.
この動画を見る
自然数$n^3+100$が$n+10$で割り切れるような最大の自然数nを求めよ.
【良問】整数問題の重要なポイントが詰まりまくった問題【数学 大学入試】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)整数$m$に対して、$m^2$を4で割った余りは0または1であることを示せ。
(2)自然数$n,k$が$25×3^n=k^2+176$・・・・・・(①)を満たすとき、$n$は偶数であることを示せ。
(3)(2)の関係式(①)を満たす自然数の組($n,k$)をすべて求めよ。
数学入試問題過去問
この動画を見る
(1)整数$m$に対して、$m^2$を4で割った余りは0または1であることを示せ。
(2)自然数$n,k$が$25×3^n=k^2+176$・・・・・・(①)を満たすとき、$n$は偶数であることを示せ。
(3)(2)の関係式(①)を満たす自然数の組($n,k$)をすべて求めよ。
数学入試問題過去問
【数A】整数の性質:結局何で割った余り?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学A 整数の性質】
3で割ると2余り、5で割ると3余り、7で割ると2余る整数を一般化せよ。
これを合同式を用いて解きます。
この動画を見る
【高校数学 数学A 整数の性質】
3で割ると2余り、5で割ると3余り、7で割ると2余る整数を一般化せよ。
これを合同式を用いて解きます。
【条件を数式に変えよ!】整数:新潟県高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
この2つの自然数の積は,この2つの自然数の和より55大きい.
連続する2つの自然数を求めなさい.
新潟県高校過去問
この動画を見る
この2つの自然数の積は,この2つの自然数の和より55大きい.
連続する2つの自然数を求めなさい.
新潟県高校過去問
【良問】面倒な作業は省略しろ!一橋大学の整数問題【数学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ 3q^3-p^2q-pq^2+3q^3=2013$を満たす正の整数$ p,q$をすべて求めよ。
一橋大過去問
この動画を見る
$ 3q^3-p^2q-pq^2+3q^3=2013$を満たす正の整数$ p,q$をすべて求めよ。
一橋大過去問
【整数問題の超難問】素数の中のあの数字を使え!一橋大学で実際に出された入試問題【数学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ a-b-8$と$b-c-8$が素数となるような素数の組$(a,b,c)$をすべて求めよ。
一橋大過去問
この動画を見る
$ a-b-8$と$b-c-8$が素数となるような素数の組$(a,b,c)$をすべて求めよ。
一橋大過去問
頻出の整数問題!難関大学でよく出る重要な性質【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ m $を整数とする。3次方程式$ x^3+mx^2+(m+8)x+1=0$は有理数の解$a$を持つ。
(1)$a$は整数であることを示せ。
(2)$m$の値を求めよ
一橋大過去問
この動画を見る
$ m $を整数とする。3次方程式$ x^3+mx^2+(m+8)x+1=0$は有理数の解$a$を持つ。
(1)$a$は整数であることを示せ。
(2)$m$の値を求めよ
一橋大過去問
難問整数問題!大事なのは指数の感覚!?【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ 6・3^{3x}+1=7・5^{2x}$を満たす$0$以上の整数$x$をすべて求めよ。
一橋大過去問
この動画を見る
$ 6・3^{3x}+1=7・5^{2x}$を満たす$0$以上の整数$x$をすべて求めよ。
一橋大過去問
整数問題の難問!君は解けるか!?【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ a^4=b^2+2^c$を満たす正の整数の組$(a,b,c)$で$a$が奇数であるものを求めよ。
一橋大過去問
この動画を見る
$ a^4=b^2+2^c$を満たす正の整数の組$(a,b,c)$で$a$が奇数であるものを求めよ。
一橋大過去問
整数問題の難問!2つの解法を紹介【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2=yz+7 \\
y^2=zx+7 \\
z^2=xy+7
\end{array}
\right.
\end{eqnarray}$
整数$(x,y,z)$を求めよ.
一橋大過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2=yz+7 \\
y^2=zx+7 \\
z^2=xy+7
\end{array}
\right.
\end{eqnarray}$
整数$(x,y,z)$を求めよ.
一橋大過去問
整数問題 筑波大附属

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
4ケタの数字3,4,5,6を並べ替えてできる4ケタの数をmとし、mの各位の数を逆順に並べてできる数をnとするとm+nは必ずpの倍数となる。
(ただしpは考えられる最大の整数)
p=?
筑波大学附属高等学校
この動画を見る
4ケタの数字3,4,5,6を並べ替えてできる4ケタの数をmとし、mの各位の数を逆順に並べてできる数をnとするとm+nは必ずpの倍数となる。
(ただしpは考えられる最大の整数)
p=?
筑波大学附属高等学校
整数の性質、これ解ける?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
正の整数$x,y(x \gt y)$と、$n \gt 1$である任意の素数$n$が$\displaystyle \frac{1}{x}+\displaystyle \frac{1}{y}=\displaystyle \frac{1}{n}$満たすとき、$x$が偶取であることを示せ。
この動画を見る
正の整数$x,y(x \gt y)$と、$n \gt 1$である任意の素数$n$が$\displaystyle \frac{1}{x}+\displaystyle \frac{1}{y}=\displaystyle \frac{1}{n}$満たすとき、$x$が偶取であることを示せ。
福田の数学〜千葉大学2022年理系第7問〜不定方程式の自然数解と漸化式で与えられた数列

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
この動画を見る
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
整数問題 初級
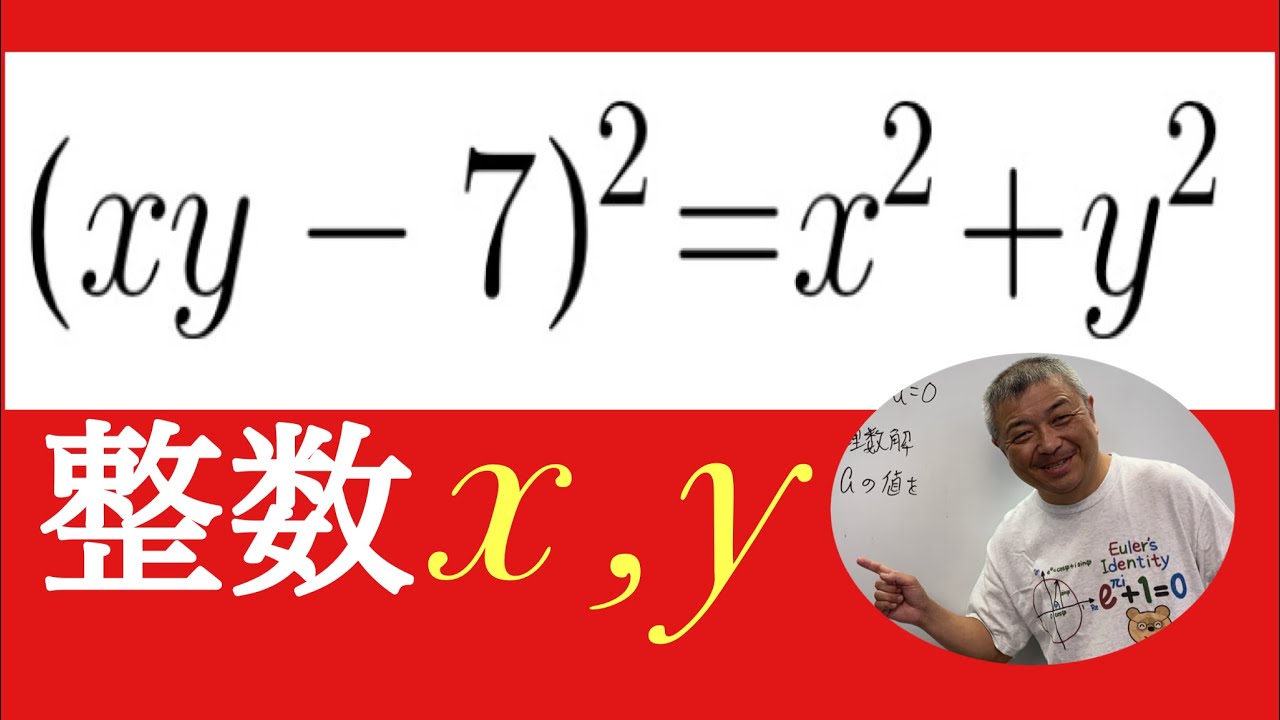
単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数(x,y)の組をすべて求めよ.
$(xy-7)^2=x^2+y^2 $
この動画を見る
整数(x,y)の組をすべて求めよ.
$(xy-7)^2=x^2+y^2 $
東大の整数問題【数学 入試問題】【東京大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$3$以上$9999$以下の奇数$a$で、$a^2-a$が$10000$で割り切れるものをすべて求めよ。
東大過去問
この動画を見る
$3$以上$9999$以下の奇数$a$で、$a^2-a$が$10000$で割り切れるものをすべて求めよ。
東大過去問
福田の数学〜千葉大学2022年理系第4問〜不定方程式とユークリッドの互除法

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
0以上9999以下の整数を4桁で表示し、以下の操作を行うこととする。
ただし、 4桁で表示するとは、整数が100以上999以下の場合は千の位の数字を0、
10以上99以下の場合は千の位と百の位の数字を0、1以上9以下の場合は
千の位と百の位と十の位の数字を0、そして0はどの位の数字も0とすることである。
操作:千の位の数字と十の位の数字を入れ換える。さらに、百の位の数字と
一の位の数字を入れ換える。
また、整数Lに対し、操作によって得られた整数を$\bar{ L }$と表す。
(1) Mを0以上9999以下の整数とし、$M=100x+y$のように整数$x, y (0 \leqq x \leqq 99,$
$ 0 \leqq y \leqq 99)$を用いて表す。操作によって得られた$\bar{ M }$ がMの
$\frac{2}{3}$倍に3を足した数 に等しいならば、
$-197x+298y = 9$が成り立つことを証明せよ。
(2) Nが0以上 9999 以下の整数ならば、操作によって
得られた整数$\bar{ N }$はNの$\frac{2}{3}$倍に1を足した数と等しくならないことを証明せよ。
2022千葉大学理系過去問
この動画を見る
0以上9999以下の整数を4桁で表示し、以下の操作を行うこととする。
ただし、 4桁で表示するとは、整数が100以上999以下の場合は千の位の数字を0、
10以上99以下の場合は千の位と百の位の数字を0、1以上9以下の場合は
千の位と百の位と十の位の数字を0、そして0はどの位の数字も0とすることである。
操作:千の位の数字と十の位の数字を入れ換える。さらに、百の位の数字と
一の位の数字を入れ換える。
また、整数Lに対し、操作によって得られた整数を$\bar{ L }$と表す。
(1) Mを0以上9999以下の整数とし、$M=100x+y$のように整数$x, y (0 \leqq x \leqq 99,$
$ 0 \leqq y \leqq 99)$を用いて表す。操作によって得られた$\bar{ M }$ がMの
$\frac{2}{3}$倍に3を足した数 に等しいならば、
$-197x+298y = 9$が成り立つことを証明せよ。
(2) Nが0以上 9999 以下の整数ならば、操作によって
得られた整数$\bar{ N }$はNの$\frac{2}{3}$倍に1を足した数と等しくならないことを証明せよ。
2022千葉大学理系過去問
整数問題 中級

【頻出】整数の証明問題【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$n$を自然数とするとき、$n^2$は$3$の倍数か、または$3$で割った余りが$1$であることを証明せよ。
(2)自然数$a,b,c$が$a^2+b^2=c^2$を満たすとき、$a,b$のうち少なくとも$1$つは$3$の倍数出あることを証明せよ。
数学入試問題過去問
この動画を見る
(1)$n$を自然数とするとき、$n^2$は$3$の倍数か、または$3$で割った余りが$1$であることを証明せよ。
(2)自然数$a,b,c$が$a^2+b^2=c^2$を満たすとき、$a,b$のうち少なくとも$1$つは$3$の倍数出あることを証明せよ。
数学入試問題過去問
難関高校の整数問題の定番です 城北

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
6を加えても6を引いても平方数となる自然数aを求めよ。
城北高等学校
この動画を見る
6を加えても6を引いても平方数となる自然数aを求めよ。
城北高等学校
整式の剰余

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2022}$を$(x-1)^3$で割った余りを求めよ.
この動画を見る
$x^{2022}$を$(x-1)^3$で割った余りを求めよ.
素数を扱え!整数問題【数学 入試問題】【千葉大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$p$は奇数である素数とし、$N=(p+1)(p+3)(p+5)$とおく。
(1)$N$は$48$の倍数であることを示せ。
(2)$N$は$144$の倍数になるような$p$の値を小さい順に$3$つ求めよ。
千葉大過去問
この動画を見る
$p$は奇数である素数とし、$N=(p+1)(p+3)(p+5)$とおく。
(1)$N$は$48$の倍数であることを示せ。
(2)$N$は$144$の倍数になるような$p$の値を小さい順に$3$つ求めよ。
千葉大過去問
整数問題 青山学院

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2+5y^2 = 21$を満たす
整数x,yの組をすべて求めよ(x>y)
青山学院高等部
この動画を見る
$x^2+5y^2 = 21$を満たす
整数x,yの組をすべて求めよ(x>y)
青山学院高等部
京大の整数問題【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
方程式$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$を満たす正の整数の組$(x,y,z)$をすべて求めよ。
京都大過去問
この動画を見る
方程式$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$を満たす正の整数の組$(x,y,z)$をすべて求めよ。
京都大過去問
琉球大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
pは素数であり,nを自然数とする.
$f(n)=n^p-n,f(n+1)-f(n)$はpの倍数であることを示せ.
琉球大過去問
この動画を見る
pは素数であり,nを自然数とする.
$f(n)=n^p-n,f(n+1)-f(n)$はpの倍数であることを示せ.
琉球大過去問
範囲を絞れ!整数問題の入試問題【東京女子大学】【数学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$a,b,c$が整数で、$1≦a≦b≦c$かつ$abc=a+b+c$のとき、$ab≦3$であることを示せ。
(2)$1≦a≦b≦c$かつ$abc=a+b+c$を満たす整数$a,b,c$をすべて求めよ。
東京女子大過去問
この動画を見る
(1)$a,b,c$が整数で、$1≦a≦b≦c$かつ$abc=a+b+c$のとき、$ab≦3$であることを示せ。
(2)$1≦a≦b≦c$かつ$abc=a+b+c$を満たす整数$a,b,c$をすべて求めよ。
東京女子大過去問
数学を数楽に

整数問題 中学生には難しい 滝高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{a^2-12}{a}$が自然数となる整数aの値をすべて求めよ。$(a \neq 0)$
滝高等学校
この動画を見る
$\frac{a^2-12}{a}$が自然数となる整数aの値をすべて求めよ。$(a \neq 0)$
滝高等学校
