 整数の性質
整数の性質
 整数の性質
整数の性質
【高校数学】ここは基本~共通テスト数学ⅠA第4問解説~【大学受験】

単元:
#数A#大学入試過去問(数学)#整数の性質#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)$$5^{ 4}=625を2^{ 4}で割ったときの余りは1に等しい。このことを用いると,不定方程式
5^{ 4}x-2^{ 4}y=1…式1$$
の整数解のうち,xが正の整数で最小になるのは
$$x=ア,y=イウ$$であることがわかる。
また,式1の整数解のうち,xが2桁の正の整数で最小になるのは$$x=エオ,y=カキク$$である。
この動画を見る
(1)$$5^{ 4}=625を2^{ 4}で割ったときの余りは1に等しい。このことを用いると,不定方程式
5^{ 4}x-2^{ 4}y=1…式1$$
の整数解のうち,xが正の整数で最小になるのは
$$x=ア,y=イウ$$であることがわかる。
また,式1の整数解のうち,xが2桁の正の整数で最小になるのは$$x=エオ,y=カキク$$である。
【高校数学】まだまだ序章~共通テスト数学ⅠA第4問解説~【大学受験】

単元:
#数A#大学入試過去問(数学)#整数の性質#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(2) 次に625²を5⁵で割ったときの余りと2⁵で割ったときの余りについて考えてみよう。
まず、\begin{eqnarray}
625² = 5^ケ
\end{eqnarray}
であり、またm=39 とすると、\begin{eqnarray}
625² = 2^ケm^2+2^コm+1
\end{eqnarray}
である。これらより、625²を5⁵で割ったときの余りと、2⁵で割ったときの余りがわかる。
この動画を見る
(2) 次に625²を5⁵で割ったときの余りと2⁵で割ったときの余りについて考えてみよう。
まず、\begin{eqnarray}
625² = 5^ケ
\end{eqnarray}
であり、またm=39 とすると、\begin{eqnarray}
625² = 2^ケm^2+2^コm+1
\end{eqnarray}
である。これらより、625²を5⁵で割ったときの余りと、2⁵で割ったときの余りがわかる。
大学入試問題#90 京都大学(2001) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y,z$:正の整数
$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$をみたす組($x,y,z$)をすべて求めよ。
出典:2001年京都大学 入試問題
この動画を見る
$x,y,z$:正の整数
$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$をみたす組($x,y,z$)をすべて求めよ。
出典:2001年京都大学 入試問題
大学入試問題#88 関西大学(2006) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$x^3+x^2-1=y(x-1)$をみたす整数の組$(x,y)$をすべて求めよ。
出典:2006年関西大学 入試問題
この動画を見る
$x^3+x^2-1=y(x-1)$をみたす整数の組$(x,y)$をすべて求めよ。
出典:2006年関西大学 入試問題
筑波大附属の整数問題

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
8a=5bを満たす自然数a,bの中で積abが100の倍数となる最も小さいaは?
筑波大学附属高等学校
この動画を見る
8a=5bを満たす自然数a,bの中で積abが100の倍数となる最も小さいaは?
筑波大学附属高等学校
大学入試問題#87 立命館大学(2018) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#立命館大学
指導講師:
ますただ
問題文全文(内容文):
$n$:整数
$\sqrt{ n^2-8n+1 }$が整数となる$n$をすべて求めよ。
出典:2018年立命館大学 入試問題
この動画を見る
$n$:整数
$\sqrt{ n^2-8n+1 }$が整数となる$n$をすべて求めよ。
出典:2018年立命館大学 入試問題
【高校数学】1次不定方程式例題演習~応用例題~ 5-9.5【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
6で割ると1余り、11で割ると5余るような自然数のうち3桁で最小のものを求めよ。
この動画を見る
6で割ると1余り、11で割ると5余るような自然数のうち3桁で最小のものを求めよ。
不定方程式の解き方

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
不定方程式の解の求め方説明動画です
この動画を見る
不定方程式の解の求め方説明動画です
11三重県教員採用試験(数学:1番 整数問題)

単元:
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
この動画を見る
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
整数問題
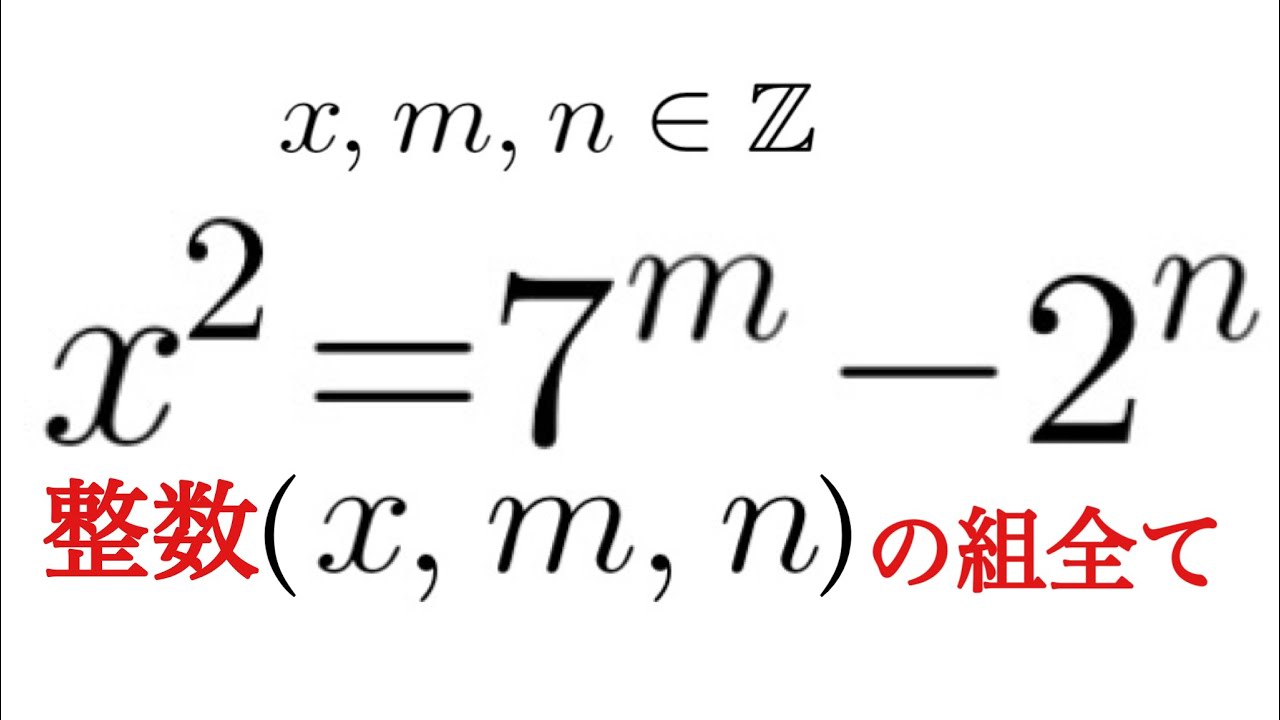
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$x,m,n$を全て求めよ.
$x^2=7^m-2^n$
この動画を見る
整数$x,m,n$を全て求めよ.
$x^2=7^m-2^n$
【高校数学】1次不定方程式~自分に合った解き方を身に付けよう~ 5-9【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$45x+32y=4$の整数解をすべて求めよ
この動画を見る
$45x+32y=4$の整数解をすべて求めよ
ガウス記号

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\left[\dfrac{x^2+1}{10}\right]+\left[\dfrac{10}{x^2+1}\right]=1$
この動画を見る
これを解け.
$\left[\dfrac{x^2+1}{10}\right]+\left[\dfrac{10}{x^2+1}\right]=1$
モスクワ数学オリンピック 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n・2^n+1$が3の倍数となる自然数$n$を求めよ.
数学オリンピックモスクワ過去問
この動画を見る
$n・2^n+1$が3の倍数となる自然数$n$を求めよ.
数学オリンピックモスクワ過去問
どっちがでかい? エレガントな解法も
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
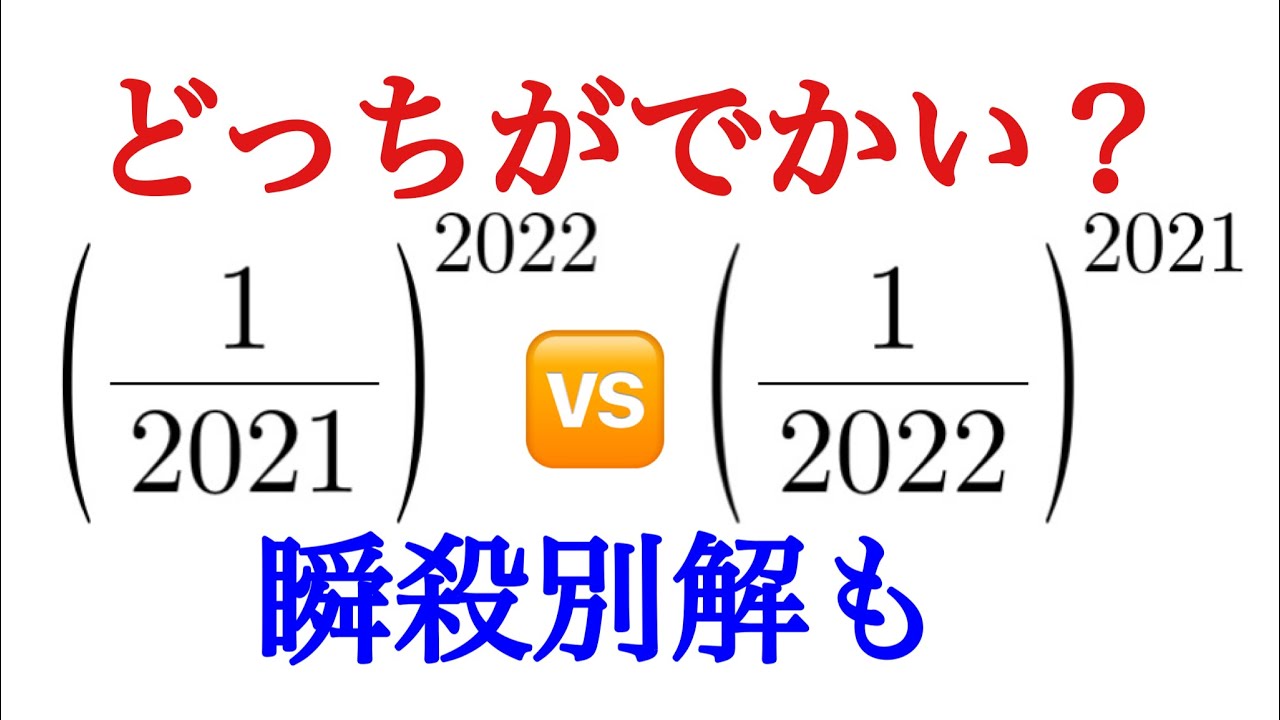
どちらが大きいか?
$\left(\dfrac{1}{2021}\right)^{2022}$VS $\left(\dfrac{1}{2022}\right)^{2021}$
この動画を見る
どちらが大きいか?
$\left(\dfrac{1}{2021}\right)^{2022}$VS $\left(\dfrac{1}{2022}\right)^{2021}$
整数問題 あの定理の証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2P^4-1237$が素数となる素数$P$をすべて求めよ.
この動画を見る
$2P^4-1237$が素数となる素数$P$をすべて求めよ.
独協医大 n進法

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$0.2_{(a)}=0.12_{(b)}$
$a,b$の値を求めよ.
独協医大過去問
この動画を見る
$0.2_{(a)}=0.12_{(b)}$
$a,b$の値を求めよ.
独協医大過去問
#48 数検1級2次 過去問 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$m,n$:正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
この動画を見る
$m,n$:正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$27^x-2・18^x+12^x=8^{x+\frac{1}{3}}$
この動画を見る
実数解を求めよ.
$27^x-2・18^x+12^x=8^{x+\frac{1}{3}}$
ざ・見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{n=1}^{10000}n^n$
$=1^1+2^2+3^3+・・・・・・9999^{9999}+10000^{10000}$を3で割った余りを求めよ.
この動画を見る
$\displaystyle \sum_{n=1}^{10000}n^n$
$=1^1+2^2+3^3+・・・・・・9999^{9999}+10000^{10000}$を3で割った余りを求めよ.
変な指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x-2^x=\sqrt{6^x}$
この動画を見る
実数解を求めよ.
$3^x-2^x=\sqrt{6^x}$
整数問題 愛知高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1から9までの自然数から異なる2つを選びa,bとする。(a<b)
$\frac{1}{a} - \frac{1}{b}$の値が最も小さくなるa,bを求めよ。
愛知高等学校
この動画を見る
1から9までの自然数から異なる2つを選びa,bとする。(a<b)
$\frac{1}{a} - \frac{1}{b}$の値が最も小さくなるa,bを求めよ。
愛知高等学校
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
この動画を見る
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
比例式と整数

単元:
#数学(中学生)#中1数学#数A#比例・反比例#整数の性質#約数・倍数・整数の割り算と余り・合同式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z,n$は自然数である.
$2x=3y=5z,x+y+z=n$である.
$\sqrt{xyz}$が整数となる$n$の条件を求めよ.
この動画を見る
$x,y,z,n$は自然数である.
$2x=3y=5z,x+y+z=n$である.
$\sqrt{xyz}$が整数となる$n$の条件を求めよ.
千葉大(医)の類題 整数
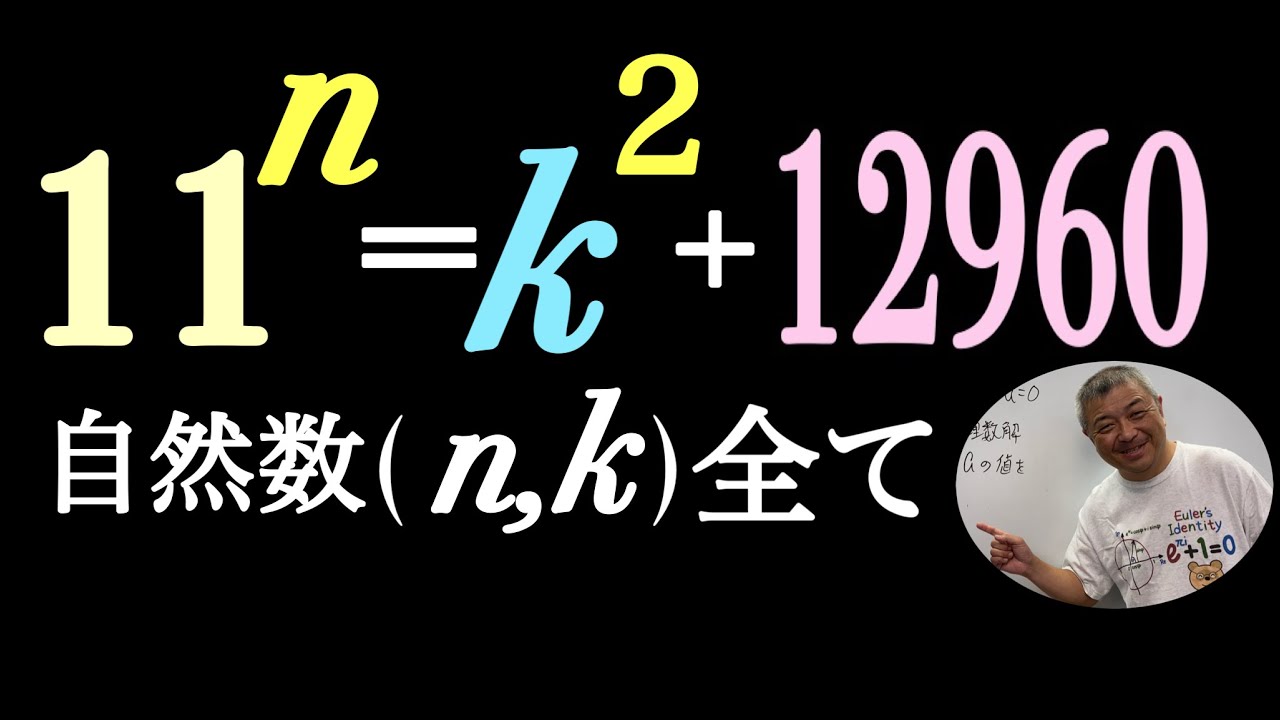
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$(n,k)$をすべて求めよ.
$11^n=k^2+12960$
千葉大(医)過去問
この動画を見る
自然数$(n,k)$をすべて求めよ.
$11^n=k^2+12960$
千葉大(医)過去問
整数問題基本

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$m,n$をすべて求めよ.
$m^4+n^4-2mn=13$
この動画を見る
整数$m,n$をすべて求めよ.
$m^4+n^4-2mn=13$
中学レベル 倍数の見分け方の証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は1~9の整数である.
$XX+YY+ZZ=XYZ$
これを解け.
この動画を見る
$x,y,z$は1~9の整数である.
$XX+YY+ZZ=XYZ$
これを解け.
すべて選べ。高校の内容だけど、中学生も知っておいて損はない。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$n(n+1)(n+5)$は何の倍数?(n:整数)
すべて選べ
(a)2の倍数
(b)3の倍数
(c)6の倍数
(d)12の倍数
この動画を見る
$n(n+1)(n+5)$は何の倍数?(n:整数)
すべて選べ
(a)2の倍数
(b)3の倍数
(c)6の倍数
(d)12の倍数
変な方程式 指数タワー
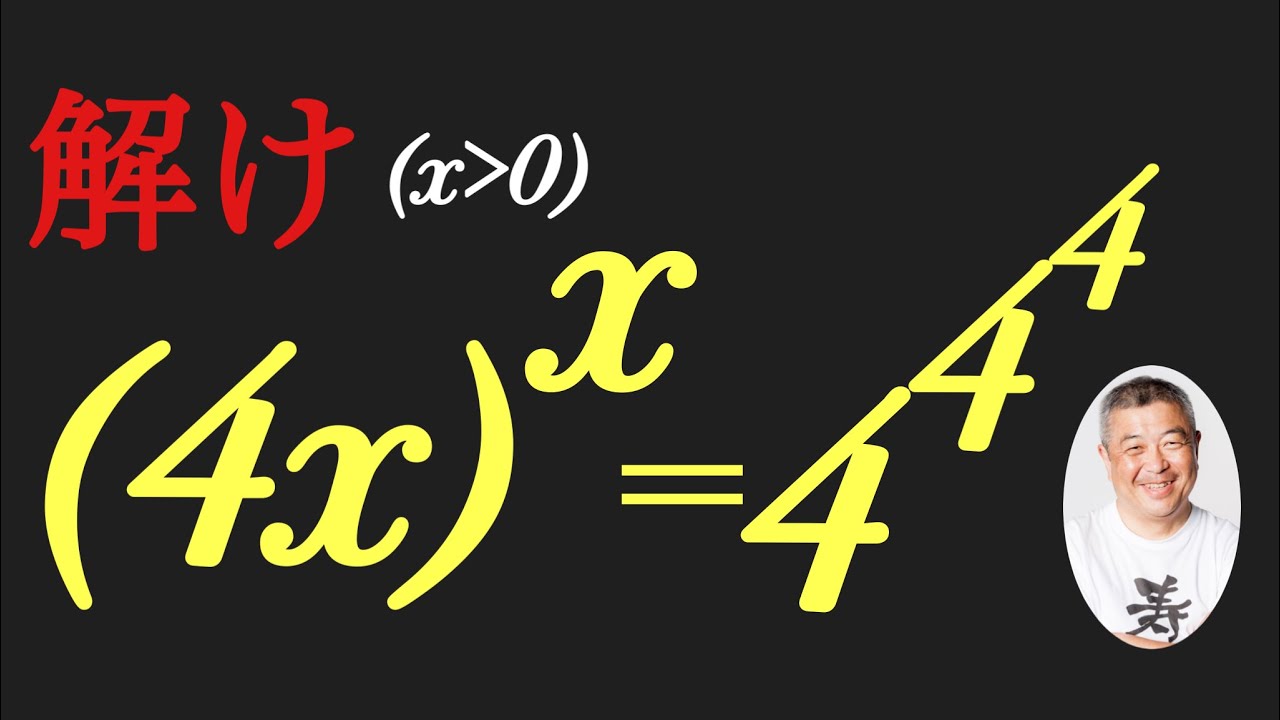
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
この動画を見る
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
変な指数方程式
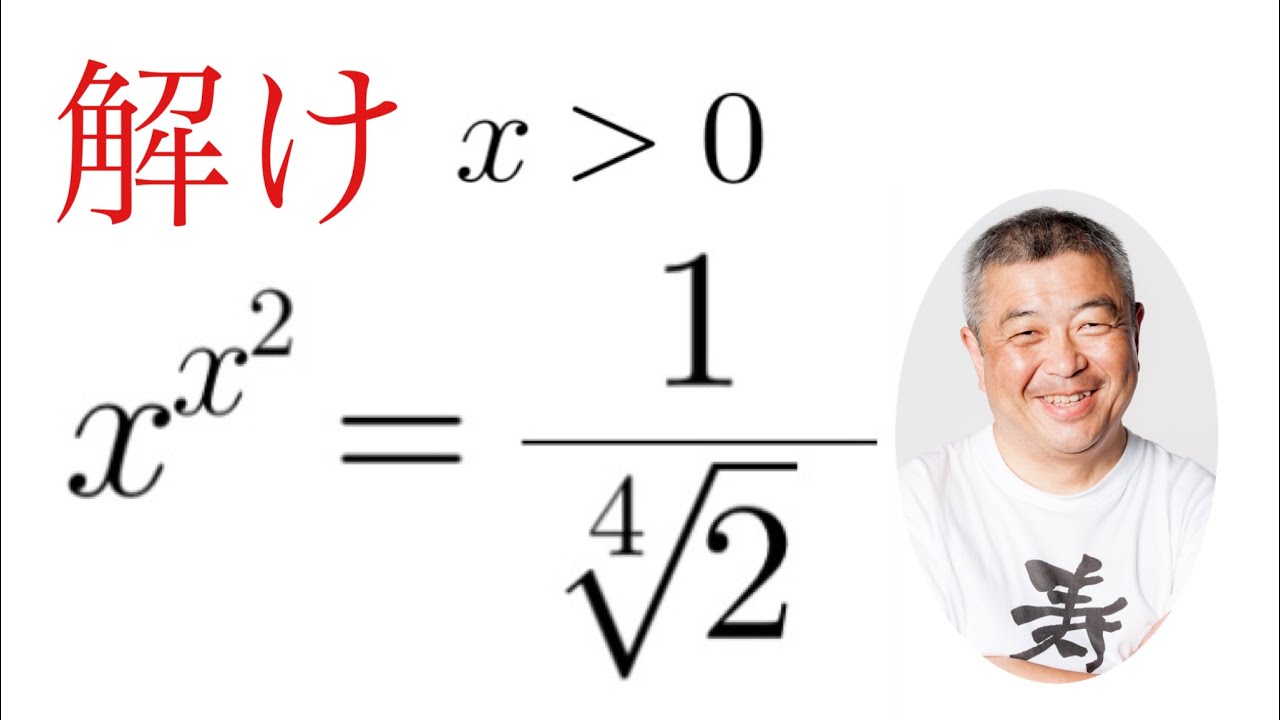
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
この動画を見る
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
2021東京海洋大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$は5以上の素数である.
$P^2-1$は$24$の倍数を示せ.
2021東京海洋大過去問
この動画を見る
$P$は5以上の素数である.
$P^2-1$は$24$の倍数を示せ.
2021東京海洋大過去問
