 整数の性質
整数の性質
 整数の性質
整数の性質
指数方程式 答えは1つじゃないよ

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
この動画を見る
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
方程式
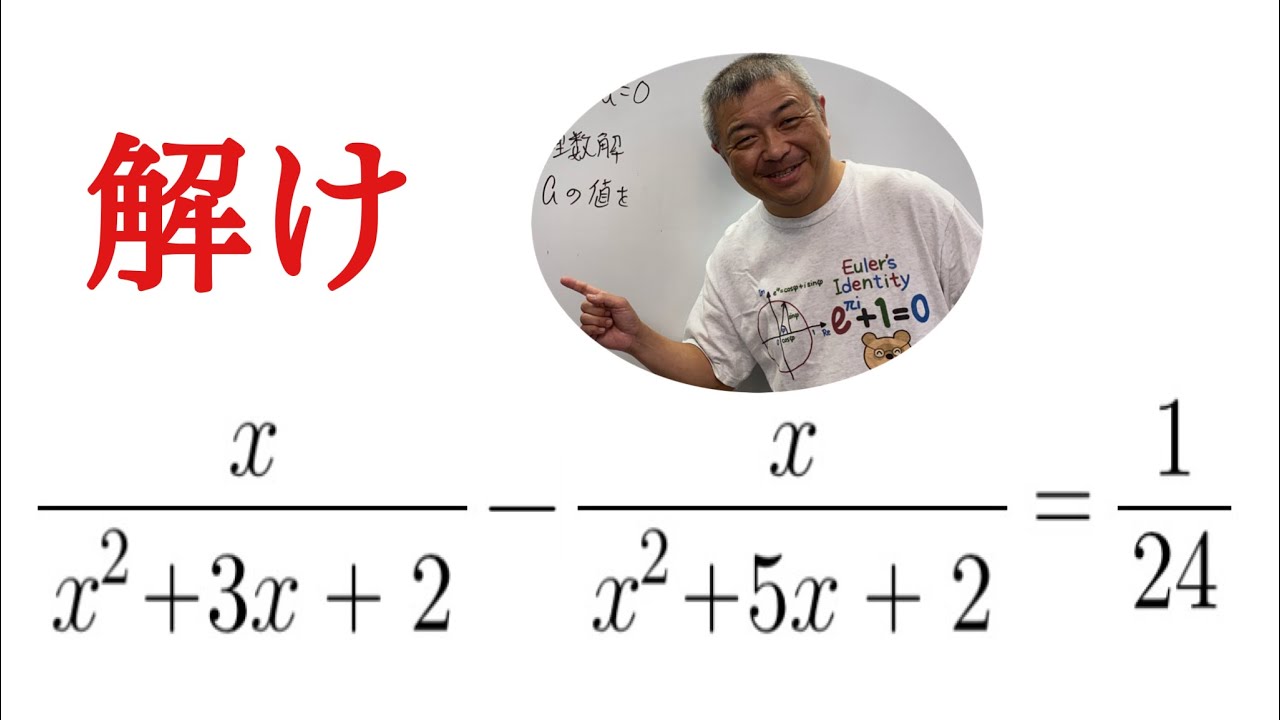
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
この動画を見る
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
未知数2で式1つの方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
この動画を見る
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
#39 数検1級1次 過去問 解と係数の関係 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
この動画を見る
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
4乗根の方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\sqrt[4]{97-x}+\sqrt[4]{x-15}=4$
この動画を見る
実数解を求めよ.
$\sqrt[4]{97-x}+\sqrt[4]{x-15}=4$
2022年問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(45+\sqrt{2022})^{2022}$の1の位を求めよ.
この動画を見る
$(45+\sqrt{2022})^{2022}$の1の位を求めよ.
コメント欄はありがたい 素晴らしい別解2つ

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a+b+c$が$6$の倍数ならば$a^3+b^3+c^3$も$6$の倍数であることを示せ.
この動画を見る
$a+b+c$が$6$の倍数ならば$a^3+b^3+c^3$も$6$の倍数であることを示せ.
整数問題 基本

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a+b+c$が$6$の倍数ならば$a^3+b^3+c^3$も$6$の倍数であることを示せ.
この動画を見る
$a+b+c$が$6$の倍数ならば$a^3+b^3+c^3$も$6$の倍数であることを示せ.
整数問題の良問

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m^2-3mn+4n^2=20$を満たす整数$m,n$は存在しない事を示せ.
この動画を見る
$m^2-3mn+4n^2=20$を満たす整数$m,n$は存在しない事を示せ.
13和歌山県教員採用試験(数学:1-(5) 整数問題)
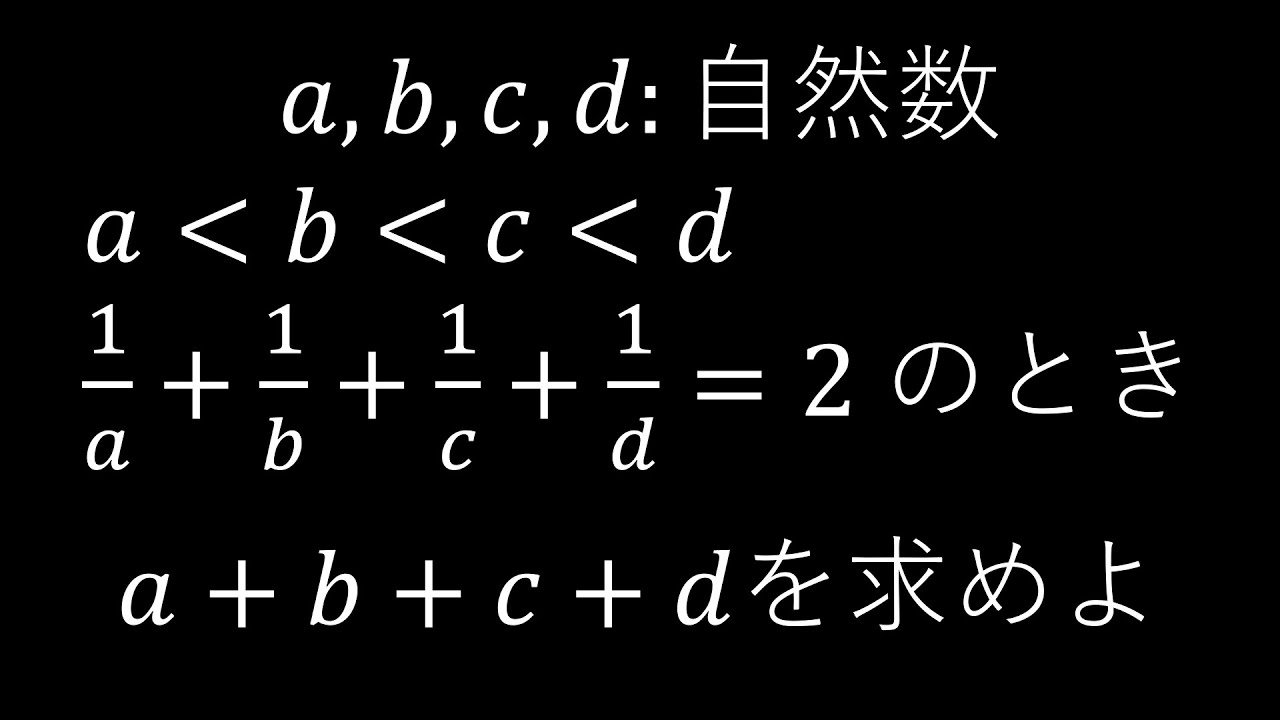
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$a,b,c,d:$自然数
$a \lt b \lt c \lt d$
$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}+\displaystyle \frac{1}{d}=2$を満たすとき$a+b+c+d$の値を求めよ
この動画を見る
$a,b,c,d:$自然数
$a \lt b \lt c \lt d$
$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}+\displaystyle \frac{1}{d}=2$を満たすとき$a+b+c+d$の値を求めよ
#31 数検1級1次 過去問 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^3-y^3=331$を満たす正の整数$x,y$を求めよ。
この動画を見る
$x^3-y^3=331$を満たす正の整数$x,y$を求めよ。
超良問⁉️だと思う整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$a,n$をすべて求めよ.
$a^{n+1}-(a+1)^n=2001$
この動画を見る
自然数$a,n$をすべて求めよ.
$a^{n+1}-(a+1)^n=2001$
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$6^{2x-3}-217・6^{x-2}+36=0$
この動画を見る
これを解け.
$6^{2x-3}-217・6^{x-2}+36=0$
整数問題の基本
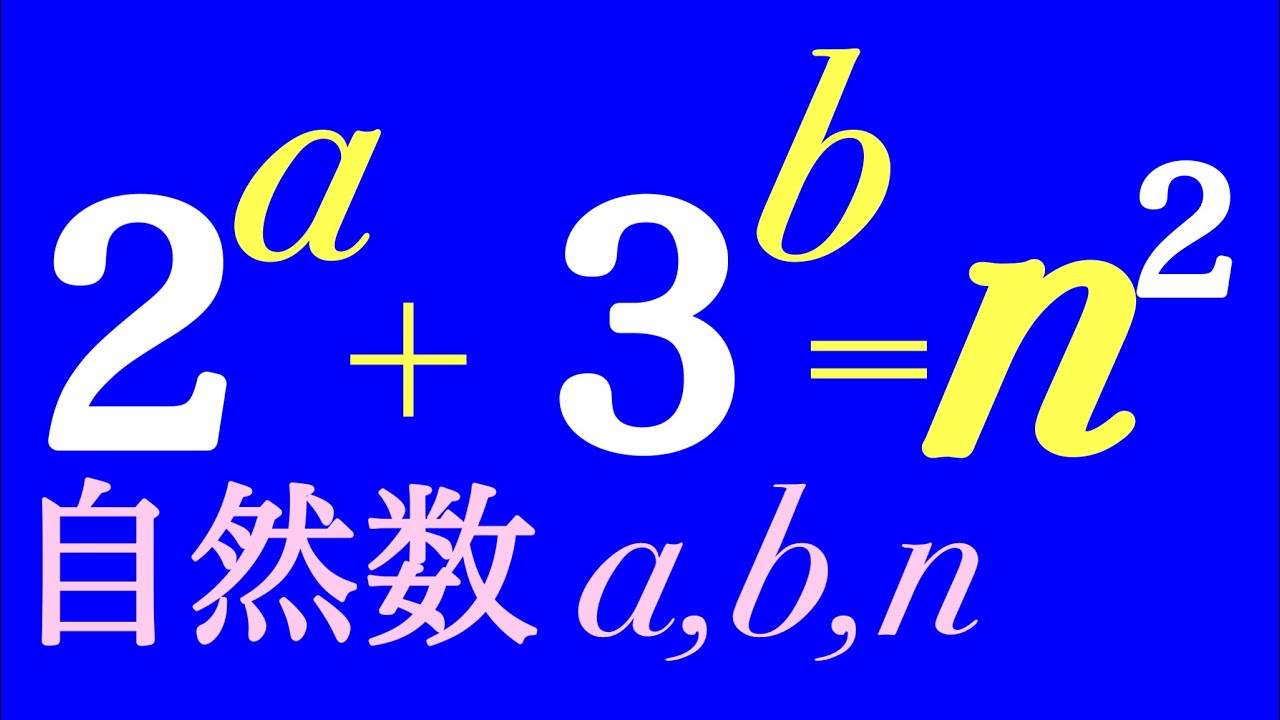
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$a,b,n$をすべて求めよ.
$2^a+3^b=n^2$
この動画を見る
自然数$a,b,n$をすべて求めよ.
$2^a+3^b=n^2$
【除法はこれでマスター】整式の除法のやり方となんで必要なのかを解説!〔高校数学 数学〕

整数の基本問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ab+cd$が$a-c$の倍数ならば,
$ad+bc$も$a-c$の倍数であることを示せ.
$a,b,c,d$は自然数である.
この動画を見る
$ab+cd$が$a-c$の倍数ならば,
$ad+bc$も$a-c$の倍数であることを示せ.
$a,b,c,d$は自然数である.
大学入試問題#39 東海大学医学部(2021) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
$n:$自然数
$n^3+100$が$n+10$で割り切れるような最大の$n$の値を求めよ。
出典:2021年東海大学医学部 入試問題
この動画を見る
$n:$自然数
$n^3+100$が$n+10$で割り切れるような最大の$n$の値を求めよ。
出典:2021年東海大学医学部 入試問題
ただの三次方程式
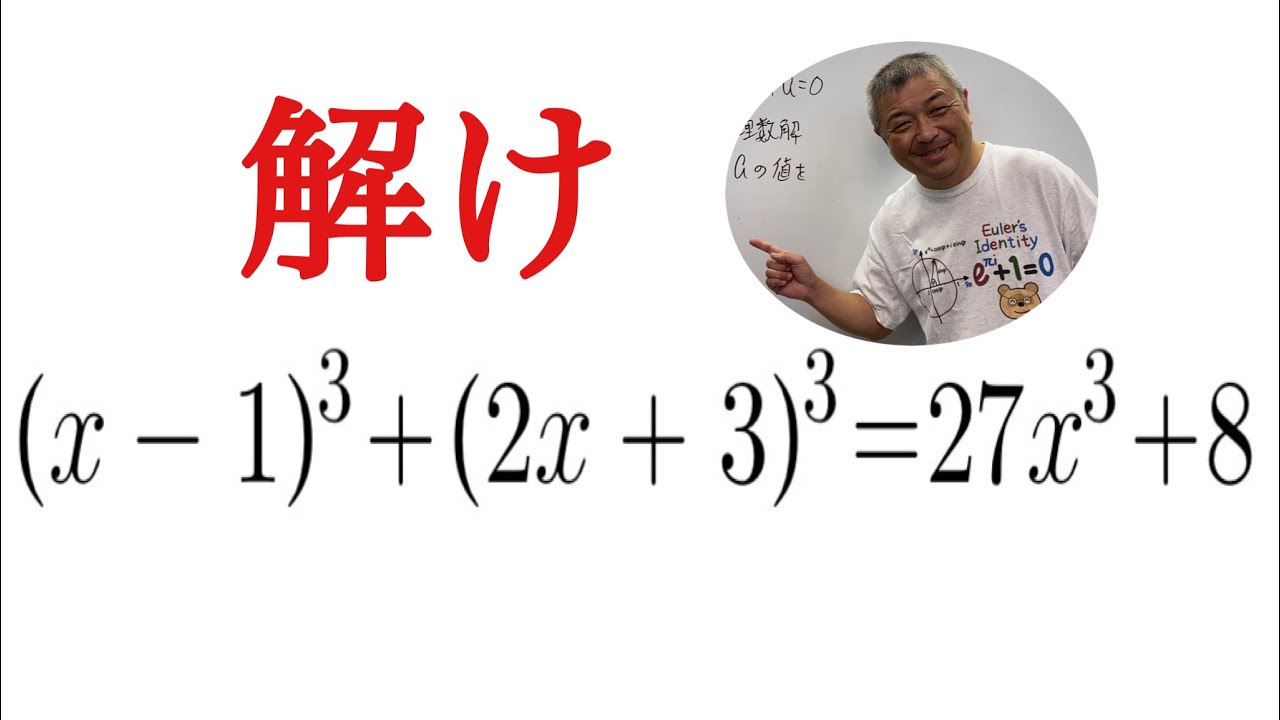
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$(x-1)^3+(2x+3)^3=27x^3+8$
この動画を見る
これを解け.
$(x-1)^3+(2x+3)^3=27x^3+8$
#27 数検1級1次 過去問 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
この動画を見る
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
変な指数方程式
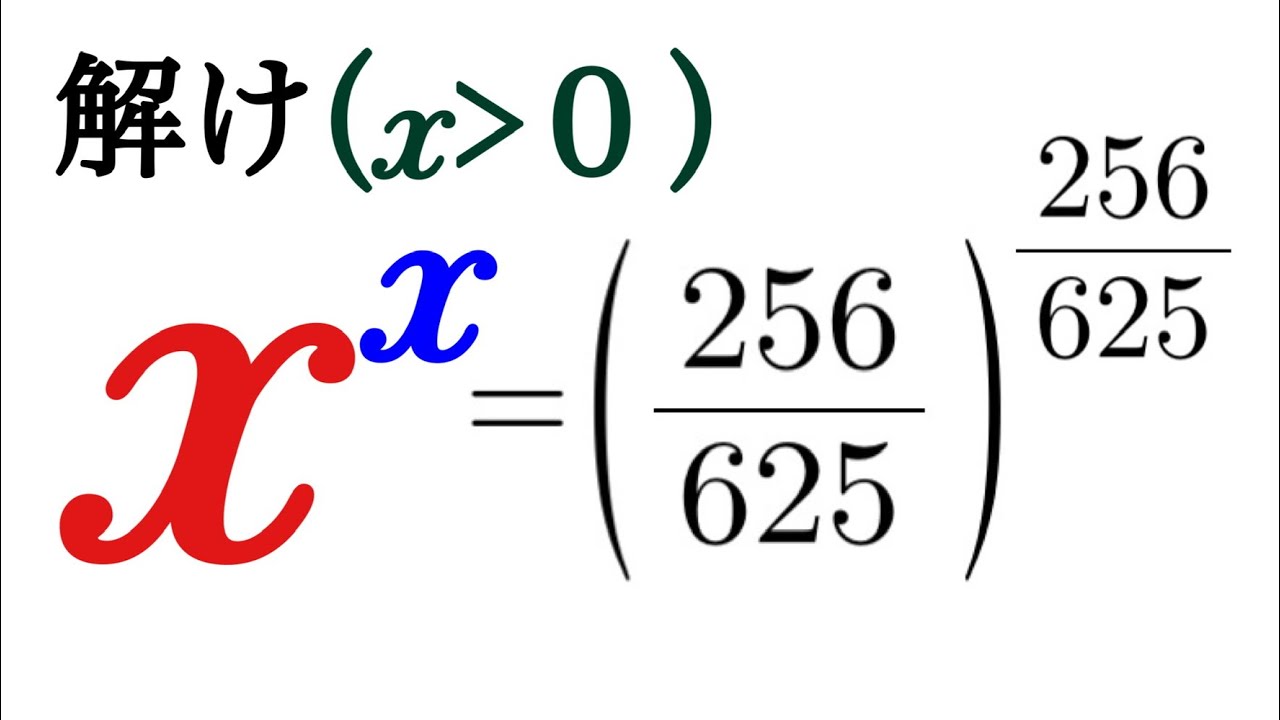
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$(x\gt 0)$
$x^x=\left(\dfrac{256}{625}\right)^{\frac{256}{625}}$
この動画を見る
これを解け.$(x\gt 0)$
$x^x=\left(\dfrac{256}{625}\right)^{\frac{256}{625}}$
整数問題
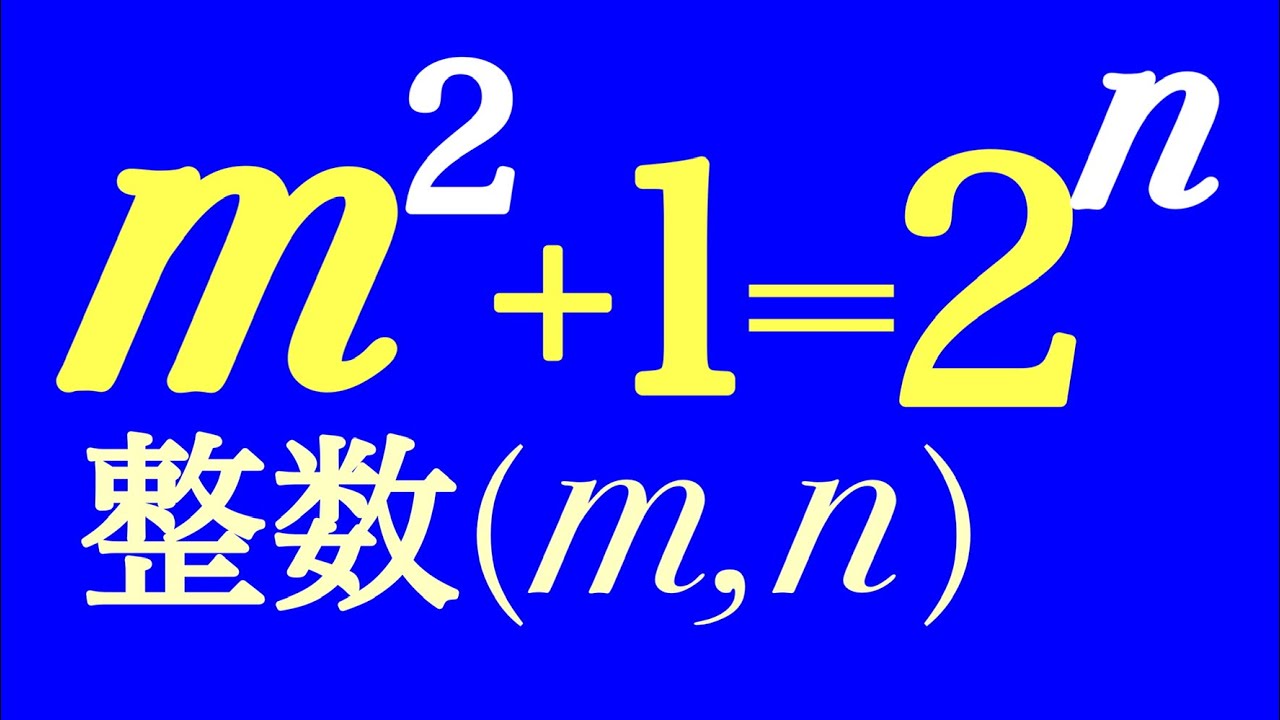
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$を整数とする.
$m^2+1=2^n$
これを解け.
この動画を見る
$m,n$を整数とする.
$m^2+1=2^n$
これを解け.
良問だぜ!自画自賛
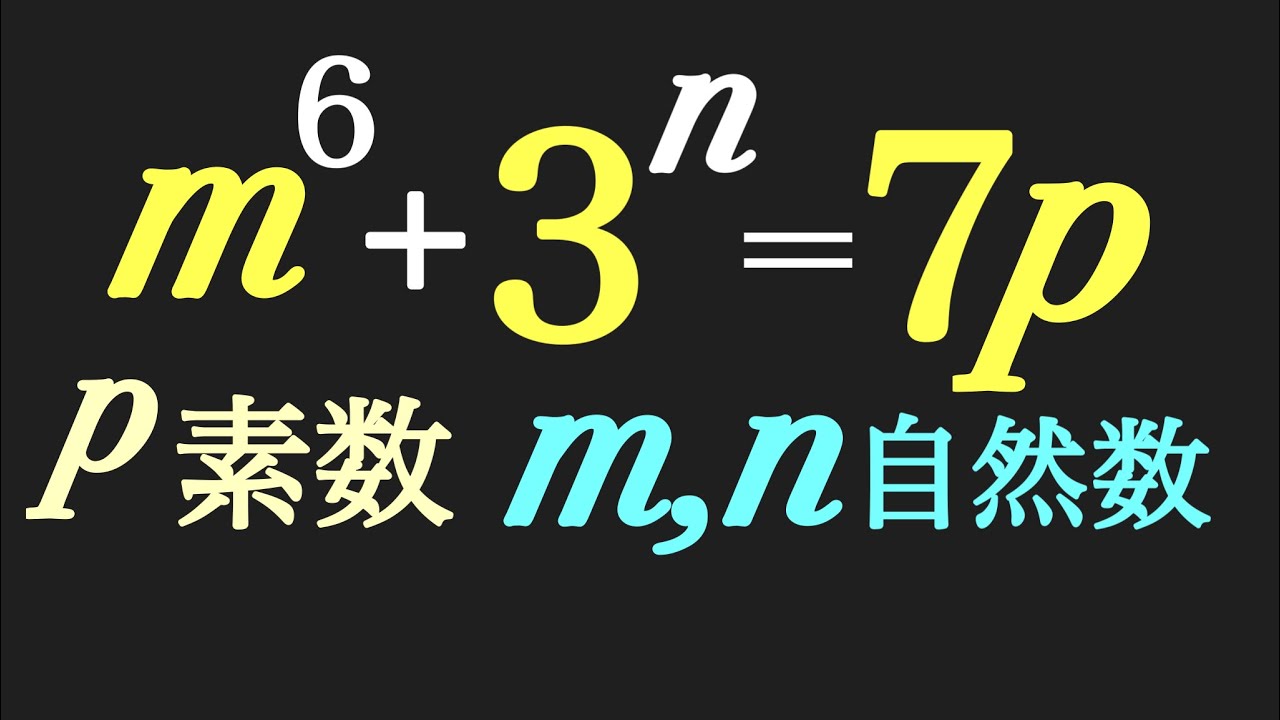
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$は自然数であり,$P$は素数である.
$m^6+3^n=7P$
これを解け.
この動画を見る
$m,n$は自然数であり,$P$は素数である.
$m^6+3^n=7P$
これを解け.
九州大の過去問をパクって問題作ってみた

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^3+3b^3=7c^3$を満たす整数$(a,b,c)$の組をすべて求めよ.
この動画を見る
$a^3+3b^3=7c^3$を満たす整数$(a,b,c)$の組をすべて求めよ.
指数方程式 解は1つではない

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x・2^{\frac{6}{x}}=72$
この動画を見る
実数解を求めよ.
$3^x・2^{\frac{6}{x}}=72$
見掛け倒しの対数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\log_{\log_6(x-3)}81=4$
この動画を見る
これを解け.
$\log_{\log_6(x-3)}81=4$
連続する五つの整数から一つ除く

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連続する5つの整数がある。そのうち1つを除いた4つの整数の和は2017となる。
除いた数を求めよ。
明治大学付属明治高等学校
この動画を見る
連続する5つの整数がある。そのうち1つを除いた4つの整数の和は2017となる。
除いた数を求めよ。
明治大学付属明治高等学校
いい問題
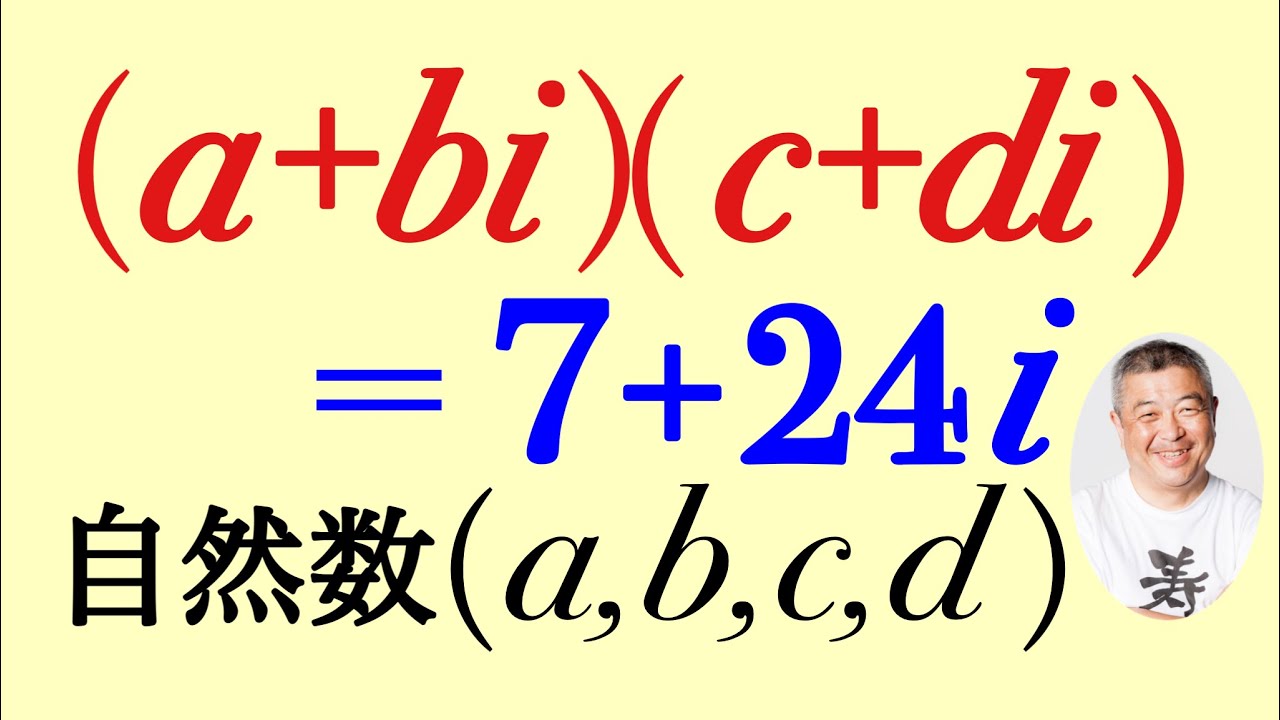
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$(a,b,c,d)$をすべて求めよ.
$(a+bi)(c+di)=7+24i$
この動画を見る
自然数$(a,b,c,d)$をすべて求めよ.
$(a+bi)(c+di)=7+24i$
不思議な方程式。優秀な視聴者様!疑問に答えて!
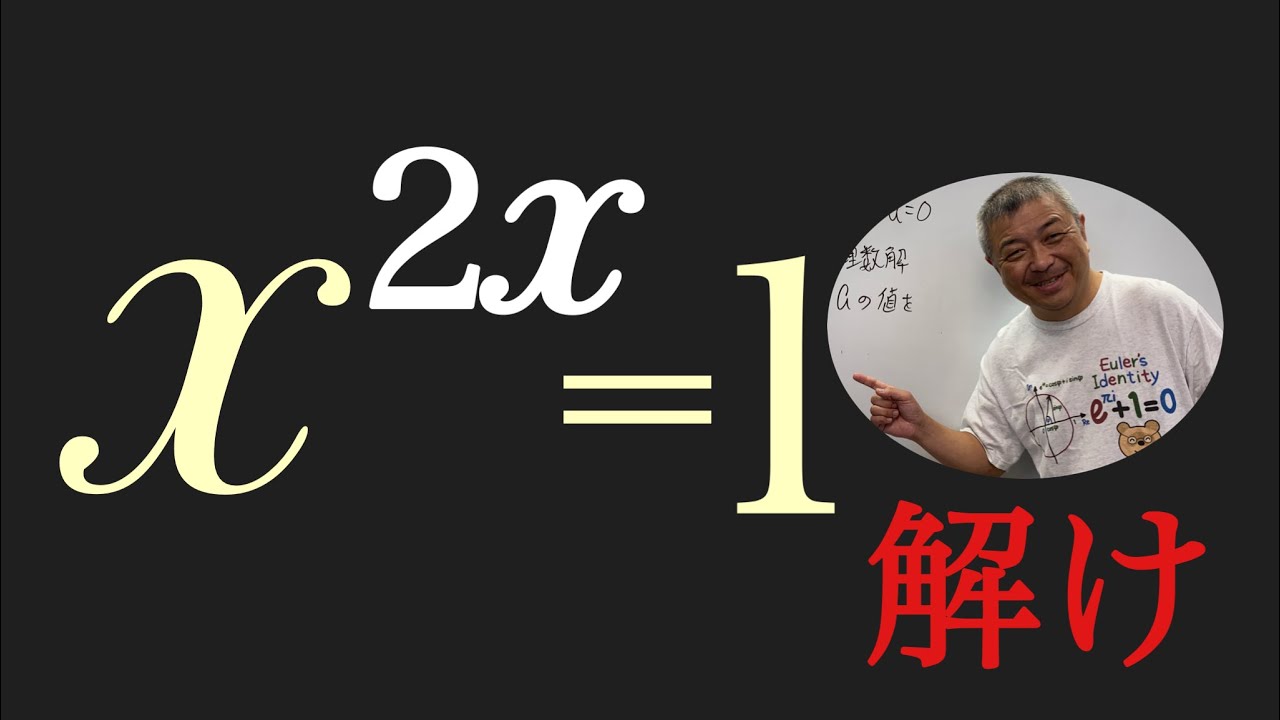
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x$は実数である.
$x^{2x}=1$
この動画を見る
これを解け.$x$は実数である.
$x^{2x}=1$
ウィルソンの定理

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$22!$を$23$で割った余りを求めよ.
$100!$を$101$で割った余りを求めよ.
この動画を見る
$22!$を$23$で割った余りを求めよ.
$100!$を$101$で割った余りを求めよ.
整数問題
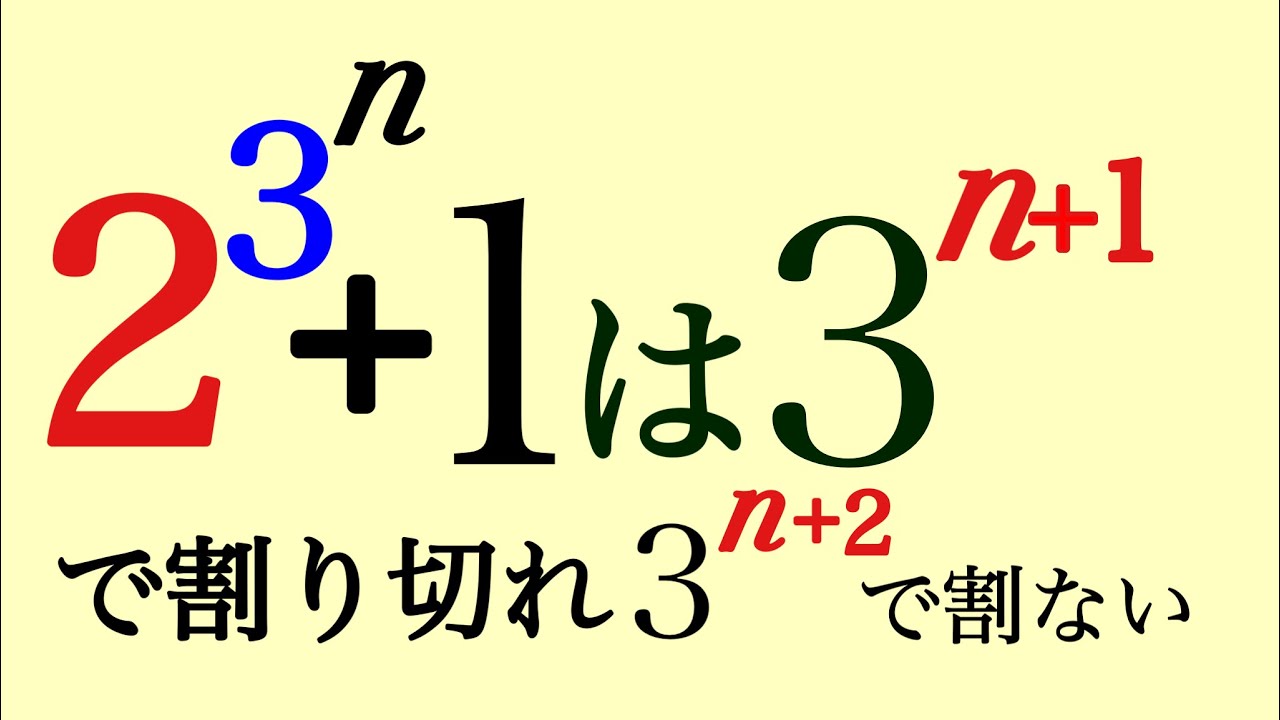
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数とする.
$2^{3^n}+1$は$3^{n+1}$で割り切れ,$3^{n+2}$では割り切れないことを示せ.
この動画を見る
$n$は自然数とする.
$2^{3^n}+1$は$3^{n+1}$で割り切れ,$3^{n+2}$では割り切れないことを示せ.
