整数の性質
整数の性質
ガウス記号・漸化式・合同式
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$[(7+\sqrt{41}^{2021}]$を$2^{2021}$で割った余りを求めよ.
この動画を見る
$[(7+\sqrt{41}^{2021}]$を$2^{2021}$で割った余りを求めよ.
【高校数学】互いに素～基本事項と使い方～ 5-4 【数学A】
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
nは整数とする。
n,n+1は互いに素であることを示せ
この動画を見る
nは整数とする。
n,n+1は互いに素であることを示せ
整数問題 京都女子
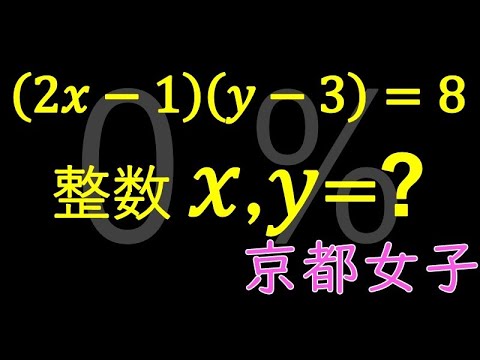
単元：
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$(2x-1)(y-3) =8$となる整数x、yの値を求めよ。
京都女子高等学校
この動画を見る
$(2x-1)(y-3) =8$となる整数x、yの値を求めよ。
京都女子高等学校
変な方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$x\sqrt[3]{x\sqrt[3]{x\sqrt[3]{x\sqrt[3]{x････}}}}=8$
この動画を見る
これを解け.
$x\sqrt[3]{x\sqrt[3]{x\sqrt[3]{x\sqrt[3]{x････}}}}=8$
【高校数学】最大公約数と最小公倍数～知識の整理～ 5-3【数学A】
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
最大公約数と最小公倍数の説明動画です
この動画を見る
最大公約数と最小公倍数の説明動画です
３乗根の方程式
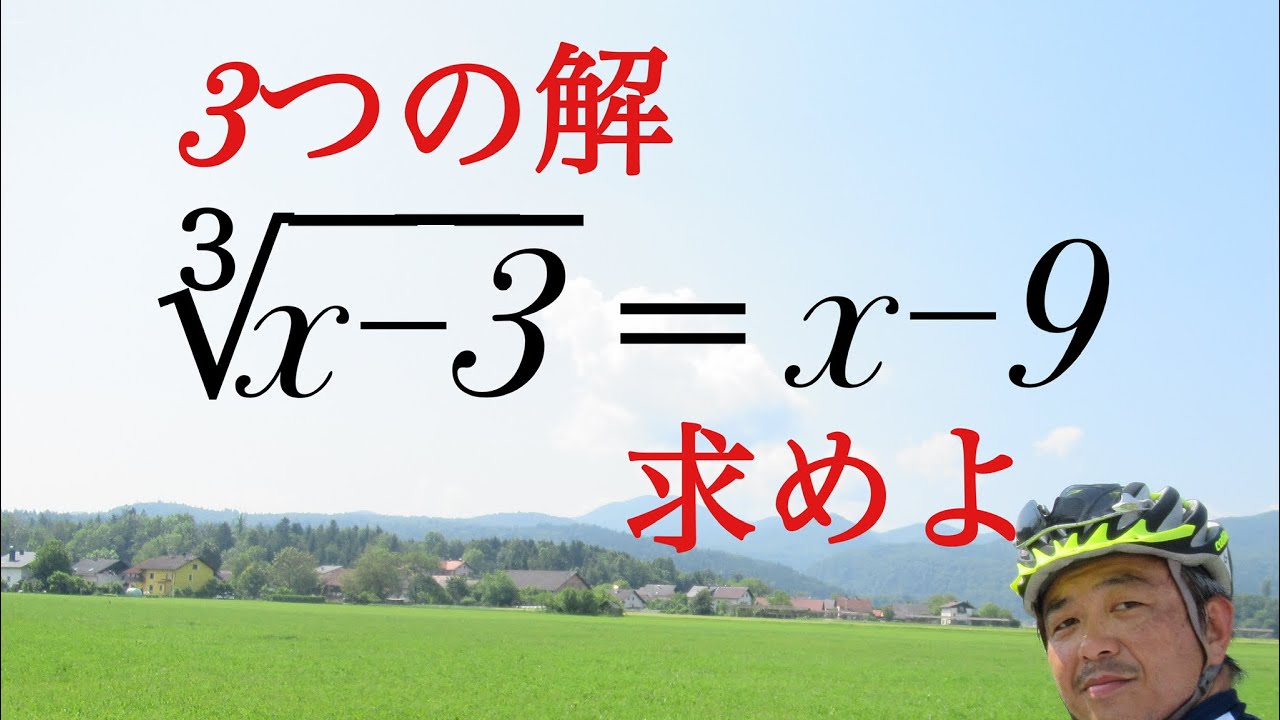
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.(解3つ)
$\sqrt[3]{x-3}=x-9$
この動画を見る
これを解け.(解3つ)
$\sqrt[3]{x-3}=x-9$
数検準1級2次（5番 整数問題）
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$ 5以上の任意の素数$p$に対して,$p^2$を$n$で割ると1余る.
最大の自然数$n$を求めよ.
①$n\leftarrow IN$
$n^2=3k$ or $3k+1 (^3k\Leftarrow IN)$
②$5\leqq p:係数$
$p=6k\pm 1 (^3k\Leftarrow IN)$
この動画を見る
$\boxed{5}$ 5以上の任意の素数$p$に対して,$p^2$を$n$で割ると1余る.
最大の自然数$n$を求めよ.
①$n\leftarrow IN$
$n^2=3k$ or $3k+1 (^3k\Leftarrow IN)$
②$5\leqq p:係数$
$p=6k\pm 1 (^3k\Leftarrow IN)$
変な方程式(数3不要)
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x\gt 0$であり実数であるとき,これを解け.
$10^{x-x^2}=x^x$
この動画を見る
$x\gt 0$であり実数であるとき,これを解け.
$10^{x-x^2}=x^x$
慶應義塾志木高校 計算の工夫
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
自然数$m$を求めよ.
$18\times 19\times 20\times 21+1=m^2$
2020慶應志木過去問
この動画を見る
自然数$m$を求めよ.
$18\times 19\times 20\times 21+1=m^2$
2020慶應志木過去問
【高校数学】素数と素因数分解～素数の基礎と無限にある証明～ 5-2【数学A】
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$\sqrt{ 540n }$が自然数になるような最小の自然数$n$を求めよ。
この動画を見る
$\sqrt{ 540n }$が自然数になるような最小の自然数$n$を求めよ。
数検準1級2次過去問【2020年12月】5番：整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$boxed{5}$ $m,n\in IN$とする.
(1)$100!=2^m \times (奇数)$と表したときの$m$の値を求めよ.
(2)$50!=n^2\times (互いに異なる素数の積)$と表したときの
素因数分解した形で表せ.
この動画を見る
$boxed{5}$ $m,n\in IN$とする.
(1)$100!=2^m \times (奇数)$と表したときの$m$の値を求めよ.
(2)$50!=n^2\times (互いに異なる素数の積)$と表したときの
素因数分解した形で表せ.
徳島大（医）整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n$は自然数とする.
$n^2(n^2+8)$の正の約数が$10$個である$n$をすべて求めよ.
2019徳島大(医)
この動画を見る
$n$は自然数とする.
$n^2(n^2+8)$の正の約数が$10$個である$n$をすべて求めよ.
2019徳島大(医)
大阪大 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$p,q$を素数とする.$(p\gt 2q)$
$p^n-4(-q)^n$がすべての自然数$n$で$3$の倍数となる$(p,q)$のうち$pq$を最小のものを求めよ.
大阪大過去問
この動画を見る
$p,q$を素数とする.$(p\gt 2q)$
$p^n-4(-q)^n$がすべての自然数$n$で$3$の倍数となる$(p,q)$のうち$pq$を最小のものを求めよ.
大阪大過去問
東工大 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(ab-1)(bc-1)(ca-1)$が$abc$で割り切れる$(a,b,c)$をすべて求めよ.
ただし,$a,b,c$は自然数であり,$1\lt a\lt b\lt c$とする.
1978東工大過去問
この動画を見る
$(ab-1)(bc-1)(ca-1)$が$abc$で割り切れる$(a,b,c)$をすべて求めよ.
ただし,$a,b,c$は自然数であり,$1\lt a\lt b\lt c$とする.
1978東工大過去問
【高校数学】約数と倍数～倍数の判別法の理解をしよう～ 5-1【数学A】
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
約数と倍数 倍数の判別法解説動画です
この動画を見る
約数と倍数 倍数の判別法解説動画です
平方根の方程式
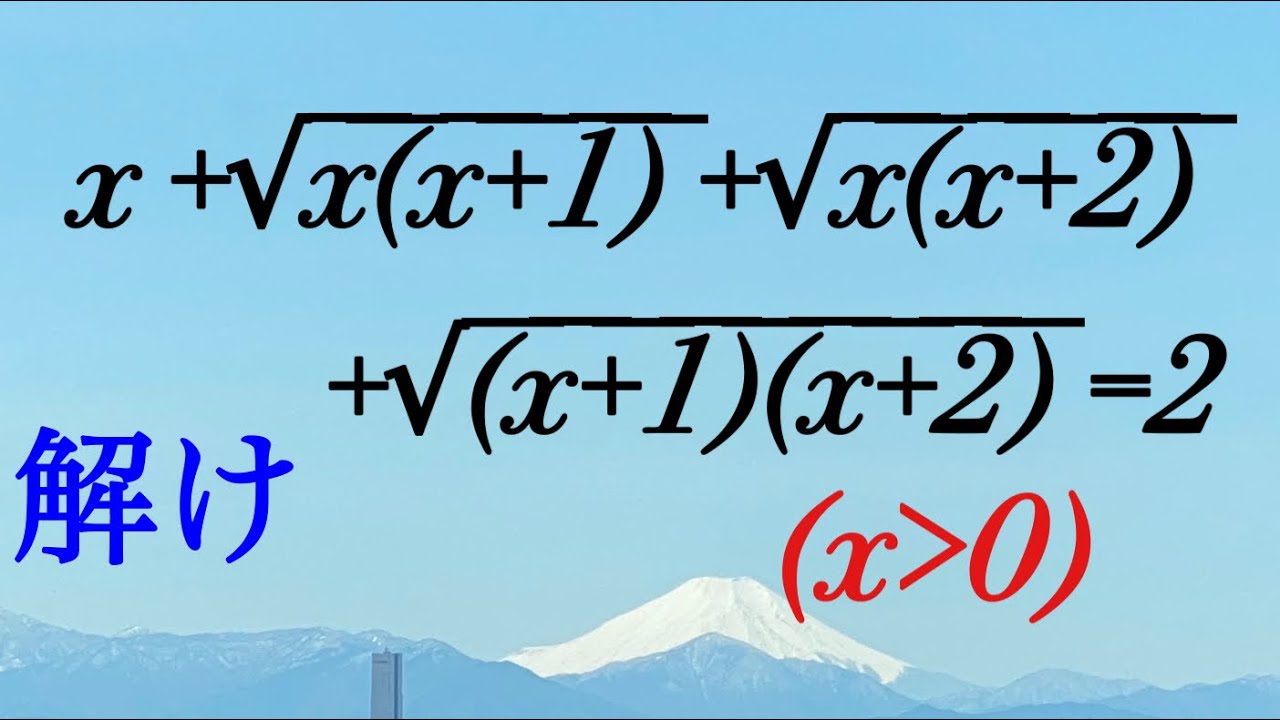
単元：
#数Ⅰ#数A#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
方程式を解け.$x$は正の実数である.
$x+\sqrt{x(x+1)}+\sqrt{x(x+2)}+$
$\sqrt{(x+1)(x+2)}=2$
この動画を見る
方程式を解け.$x$は正の実数である.
$x+\sqrt{x(x+1)}+\sqrt{x(x+2)}+$
$\sqrt{(x+1)(x+2)}=2$
整数問題（フェルマーの小定理）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$3^n+5^n-1$が$7$の倍数となる自然数$n$の条件を求めよ.
この動画を見る
$3^n+5^n-1$が$7$の倍数となる自然数$n$の条件を求めよ.
【数Ａ】整数の性質：pを素数、aとbを自然数とする。p=a³-b³のとき、p-1が6の倍数であることを証明せよ。
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
pを素数、aとbを自然数とする。$p=a^3-b^3$のとき、p-1が6の倍数であることを証明せよ。
この動画を見る
pを素数、aとbを自然数とする。$p=a^3-b^3$のとき、p-1が6の倍数であることを証明せよ。
東北大 対数方程式
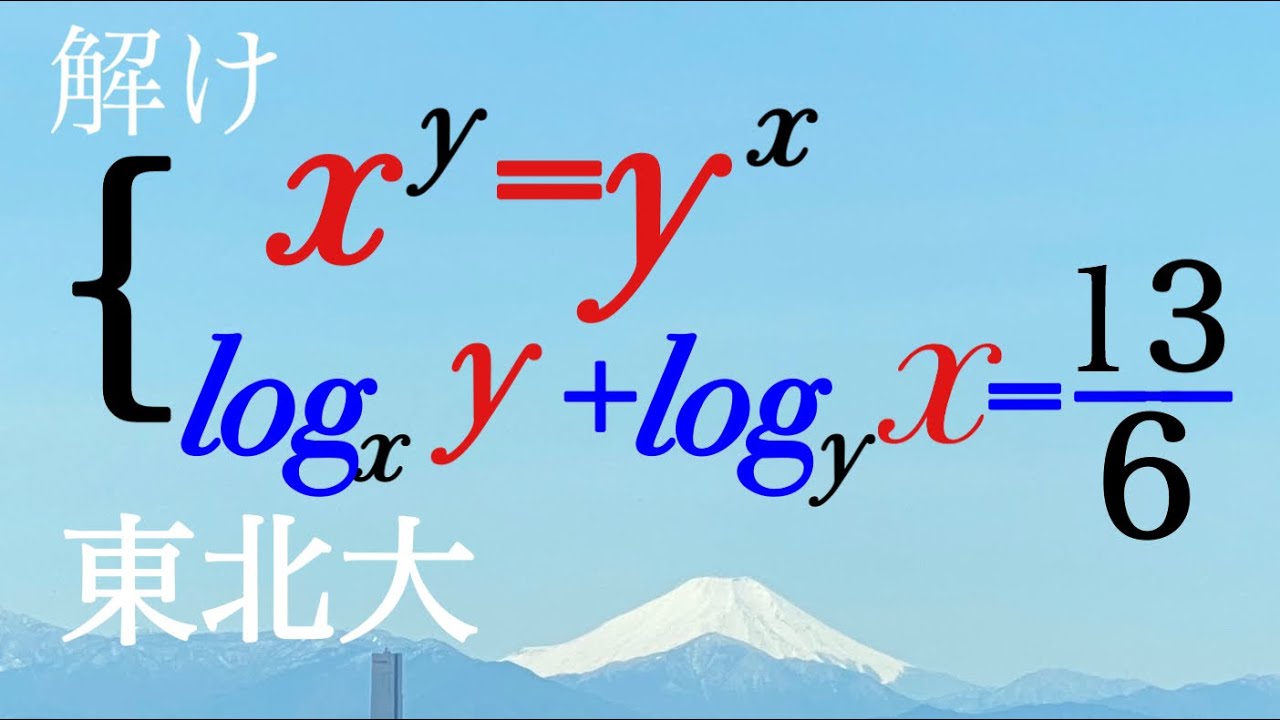
単元：
#数A#数Ⅱ#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^y=y^x \\
\log_x y+\log_y x=\dfrac{13}{6}
\end{array}
\right.
\end{eqnarray}$
東北大過去問
この動画を見る
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^y=y^x \\
\log_x y+\log_y x=\dfrac{13}{6}
\end{array}
\right.
\end{eqnarray}$
東北大過去問
【数Ａ】整数の性質：n³+5nが6の倍数であることを証明せよ。
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$n^3+5n$が6の倍数であることを証明せよ。
この動画を見る
$n^3+5n$が6の倍数であることを証明せよ。
２０２１問題
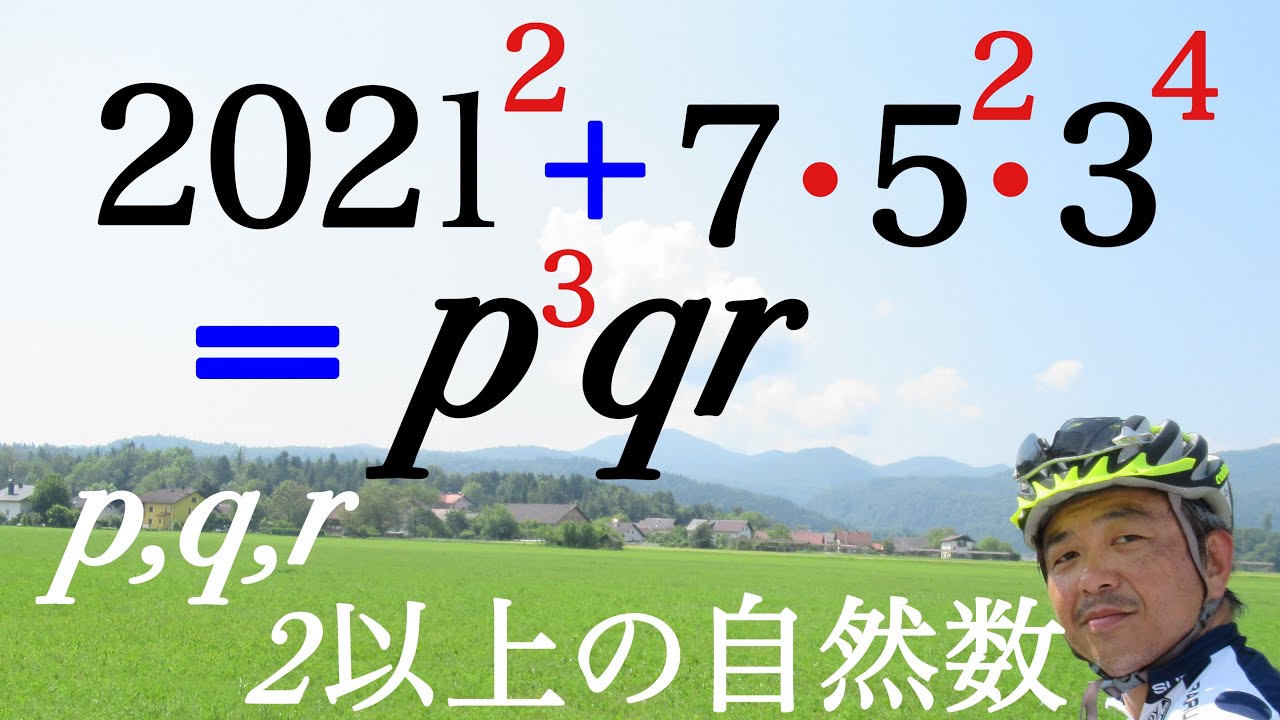
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$2021^2+7・5^2・3^4=p^3qr$
$p,q,r$は2以上の自然数である.
この動画を見る
これを解け.
$2021^2+7・5^2・3^4=p^3qr$
$p,q,r$は2以上の自然数である.
04神奈川県教員採用試験（数学：1番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
1⃣$x,y \in \mathbb{N}$ , $1 \leqq x, y \leqq 9$
$\frac{10+x}{10x+y} = \frac{1}{y}$
をみたす組(x,y)を全て求めよ。
この動画を見る
1⃣$x,y \in \mathbb{N}$ , $1 \leqq x, y \leqq 9$
$\frac{10+x}{10x+y} = \frac{1}{y}$
をみたす組(x,y)を全て求めよ。
東大 不定方程式
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x,y,z$は自然数とする.
①$x+y+z=xyz$を満たす$(x,y,z)$をすべて求めよ.$(x\leqq y\leqq z)$
②$x^3+y^3+z^3=xyz$を満たす$(x,y,z)$は存在しないことを示せ.
2006東大過去問
この動画を見る
$x,y,z$は自然数とする.
①$x+y+z=xyz$を満たす$(x,y,z)$をすべて求めよ.$(x\leqq y\leqq z)$
②$x^3+y^3+z^3=xyz$を満たす$(x,y,z)$は存在しないことを示せ.
2006東大過去問
北海道大 整数
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x,y$を自然数とする.
(1)$\dfrac{3x}{x^2+2}$が自然数となる$x$を求めよ.
(2)$\dfrac{3x}{x^2+2}+\dfrac{1}{y}$が自然数となる$(x,y)$を求めよ.
2016北海道大過去問
この動画を見る
$x,y$を自然数とする.
(1)$\dfrac{3x}{x^2+2}$が自然数となる$x$を求めよ.
(2)$\dfrac{3x}{x^2+2}+\dfrac{1}{y}$が自然数となる$(x,y)$を求めよ.
2016北海道大過去問
津田塾大 基本対称式
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b,c$は自然数である.
$abc,ab+bc+ca$,$a+b+c$がすべて3の倍数なら,$a,b,c$はすべて3の倍数であることを示せ.
2016津田塾大過去問
この動画を見る
$a,b,c$は自然数である.
$abc,ab+bc+ca$,$a+b+c$がすべて3の倍数なら,$a,b,c$はすべて3の倍数であることを示せ.
2016津田塾大過去問
聖マリアンナ医大 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$p$は素数であり,$x,y,z$は整数である.
$x^3+py^3+p^2z^3-p^3xyz=0$ならば,$x=y=z=0$であることを示せ.
2016聖マリアンナ医大過去問
この動画を見る
$p$は素数であり,$x,y,z$は整数である.
$x^3+py^3+p^2z^3-p^3xyz=0$ならば,$x=y=z=0$であることを示せ.
2016聖マリアンナ医大過去問
整数問題２０２１
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$2021^{2021^{2021}}$の下3桁を求めよ.
この動画を見る
$2021^{2021^{2021}}$の下3桁を求めよ.
２０２１！を５の５０４乗で割ったあまり
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$2021!$を$5^{504}$で割った余りを求めよ.
この動画を見る
$2021!$を$5^{504}$で割った余りを求めよ.
旭川医科大 整数
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
p^3-q^3-27r^3-9pqr=0 \\
p^2-10q-30r=11
\end{array}
\right.
\end{eqnarray}$
を満たす自然数$(p,q,r)$の組をすべて求めよ.
2015旭川医科大過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
p^3-q^3-27r^3-9pqr=0 \\
p^2-10q-30r=11
\end{array}
\right.
\end{eqnarray}$
を満たす自然数$(p,q,r)$の組をすべて求めよ.
2015旭川医科大過去問
15愛知県教員採用試験（数学：1番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$x,y \in \mathbb{N}$ , $7x+4y=175$
(1)(x,y)の個数
(2)|x-y|の最大値
この動画を見る
$x,y \in \mathbb{N}$ , $7x+4y=175$
(1)(x,y)の個数
(2)|x-y|の最大値