 数A
数A
 数A
数A
整数問題・フェルマーの小定理の利用

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2023^4+1$を素因数分解したときの2以外の素因数を1つ挙げよ.
この動画を見る
$2023^4+1$を素因数分解したときの2以外の素因数を1つ挙げよ.
四捨五入

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
20で割って、小数第一位を四捨五入すると17になるような最大の整数と最小の整数を求めよ
この動画を見る
20で割って、小数第一位を四捨五入すると17になるような最大の整数と最小の整数を求めよ
関西医科大

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
この動画を見る
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
あなたもダマされる

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$x \times x = 2 \times 2$
この動画を見る
方程式を解け
$x \times x = 2 \times 2$
気付けば、知っていれば一瞬!!
福田の数学〜北海道大学2023年理系第4問〜絶対値の和の最小となる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ nを2以上の自然数とする。1個のさいころをn回投げて出た目の数を順に$a_1$, $a_2$, ... ,$a_n$とし、
$K_n$=|1-$a_1$|+|$a_1$-$a_2$|+...+|$a_{n-1}$-$a_n$|+|$a_n$-6|
とおく。また$K_n$のとりうる値の最小値を$q_n$とする。
(1)$K_3$=5となる確率を求めよ。
(2)$q_n$を求めよ。また、$K_n$=$q_n$となるための$a_1$, $a_2$,...,$a_n$に関する必要十分条件を求めよ。
(3)nを4以上の自然数とする。$L_n$=$K_n$+|$a_4$-4|とおき、$L_n$のとりうる値の最小値を$r_n$とする。$L_n$=$r_n$となる確率$p_n$を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{4}$ nを2以上の自然数とする。1個のさいころをn回投げて出た目の数を順に$a_1$, $a_2$, ... ,$a_n$とし、
$K_n$=|1-$a_1$|+|$a_1$-$a_2$|+...+|$a_{n-1}$-$a_n$|+|$a_n$-6|
とおく。また$K_n$のとりうる値の最小値を$q_n$とする。
(1)$K_3$=5となる確率を求めよ。
(2)$q_n$を求めよ。また、$K_n$=$q_n$となるための$a_1$, $a_2$,...,$a_n$に関する必要十分条件を求めよ。
(3)nを4以上の自然数とする。$L_n$=$K_n$+|$a_4$-4|とおき、$L_n$のとりうる値の最小値を$r_n$とする。$L_n$=$r_n$となる確率$p_n$を求めよ。
2023北海道大学理系過去問
ただの素因数分解

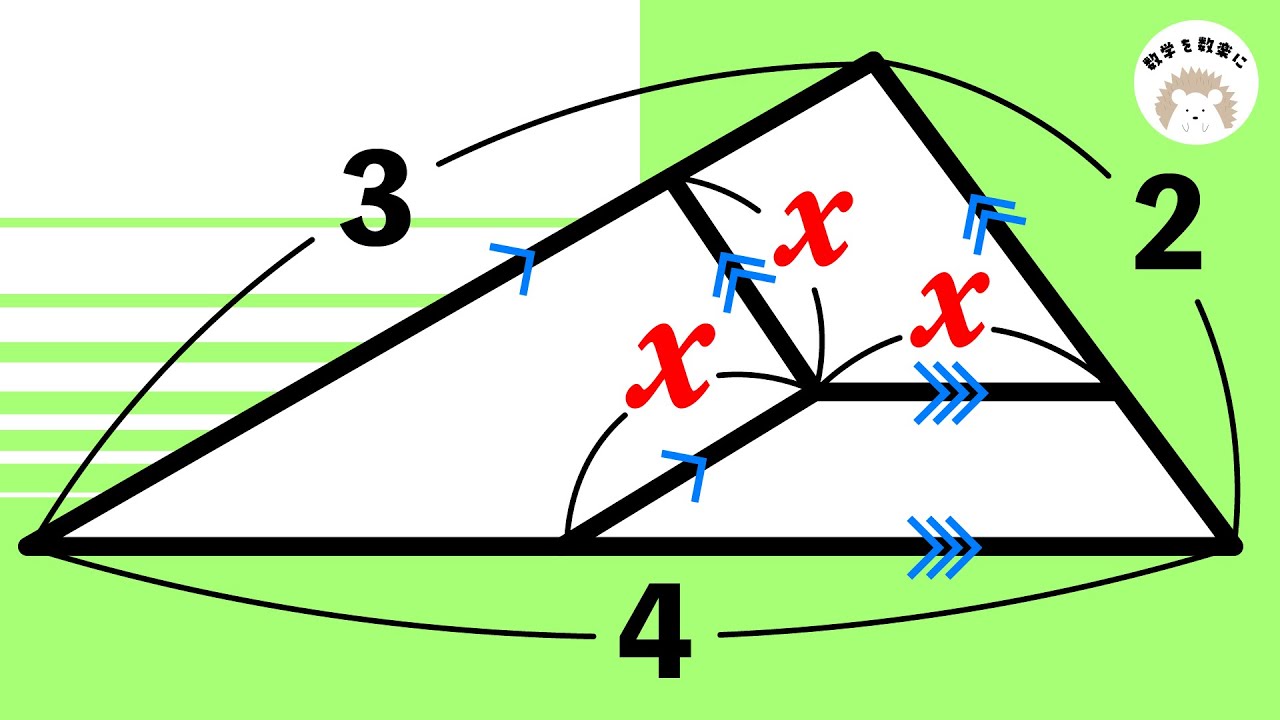
補助線引ける?
整数問題
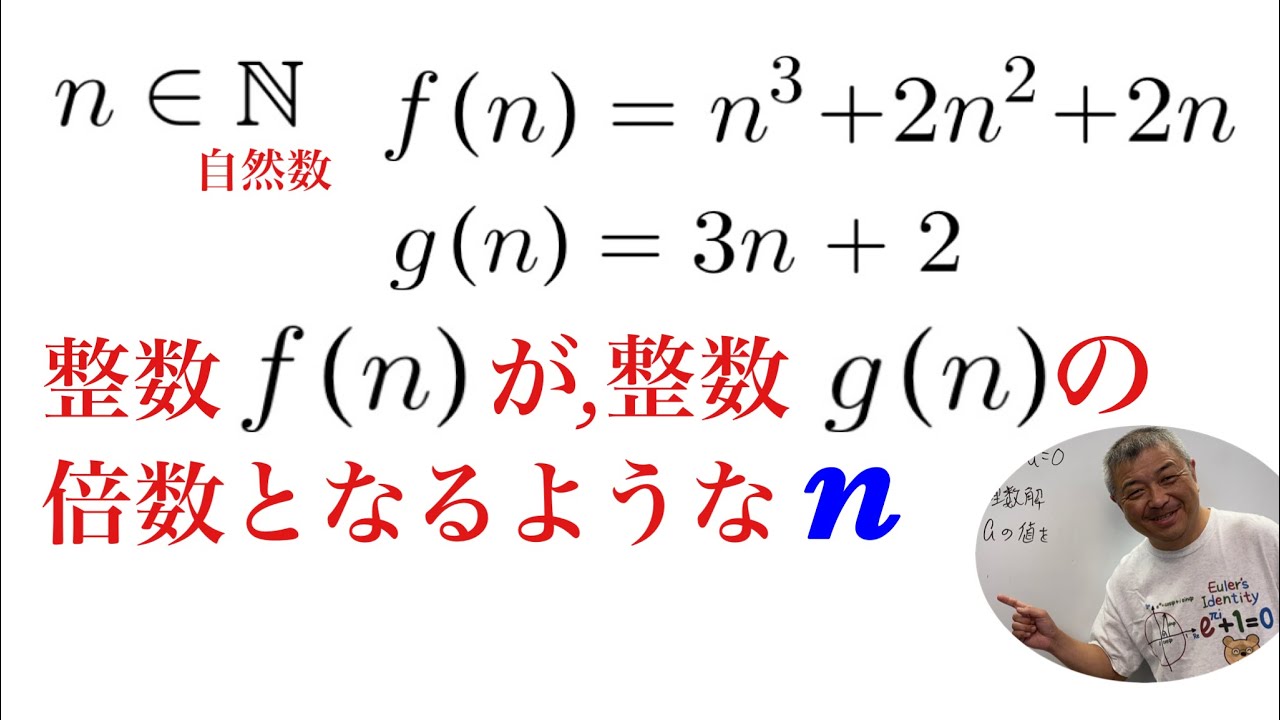
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$f(n)=n^3+2n^2+2n$
$g(n)=3n+2$
整数$f(n)$は整数$g(n)$の倍数である.
nをすべて求めよ.
この動画を見る
$n$は自然数である.
$f(n)=n^3+2n^2+2n$
$g(n)=3n+2$
整数$f(n)$は整数$g(n)$の倍数である.
nをすべて求めよ.
気付けば一瞬!
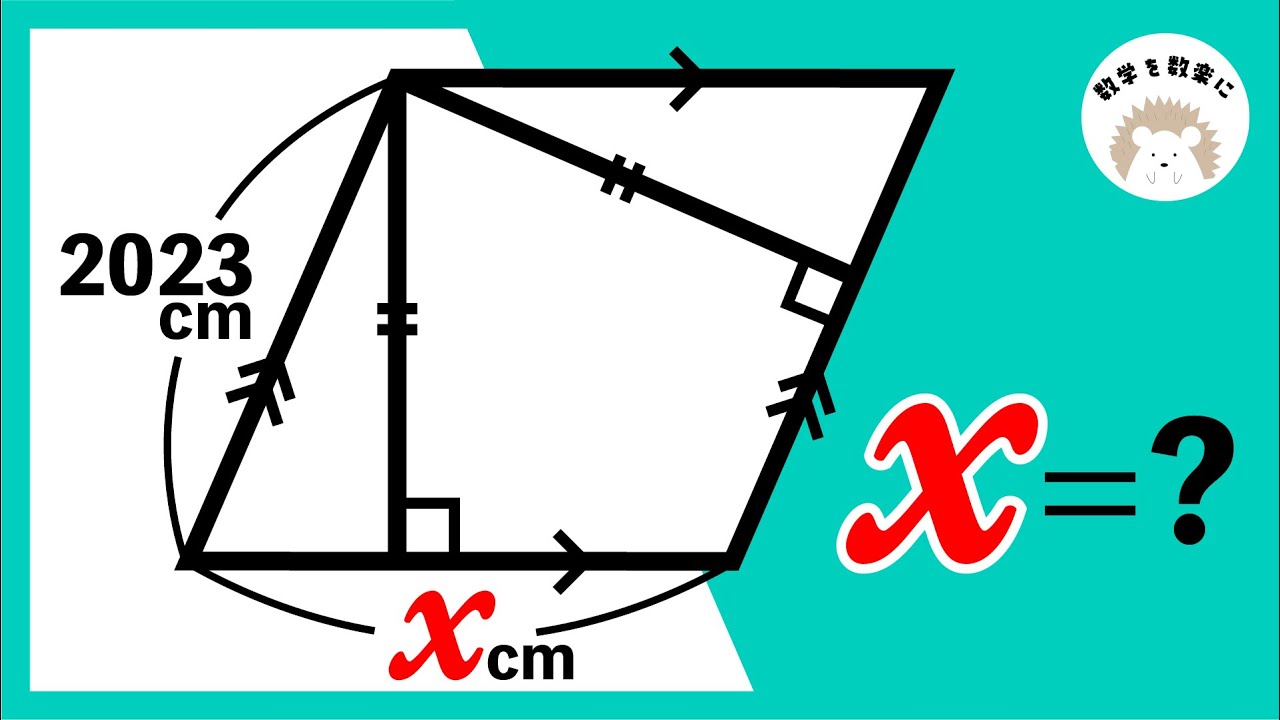
場合分けの嵐 新高1見て

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$(a^2-1)x^2 = a - 1$
(aは定数)
この動画を見る
方程式を解け
$(a^2-1)x^2 = a - 1$
(aは定数)
ざ・見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$11^{2023}+13^{2023}を144で割った余りを求めよ.$
この動画を見る
$11^{2023}+13^{2023}を144で割った余りを求めよ.$
気付けば一瞬!?
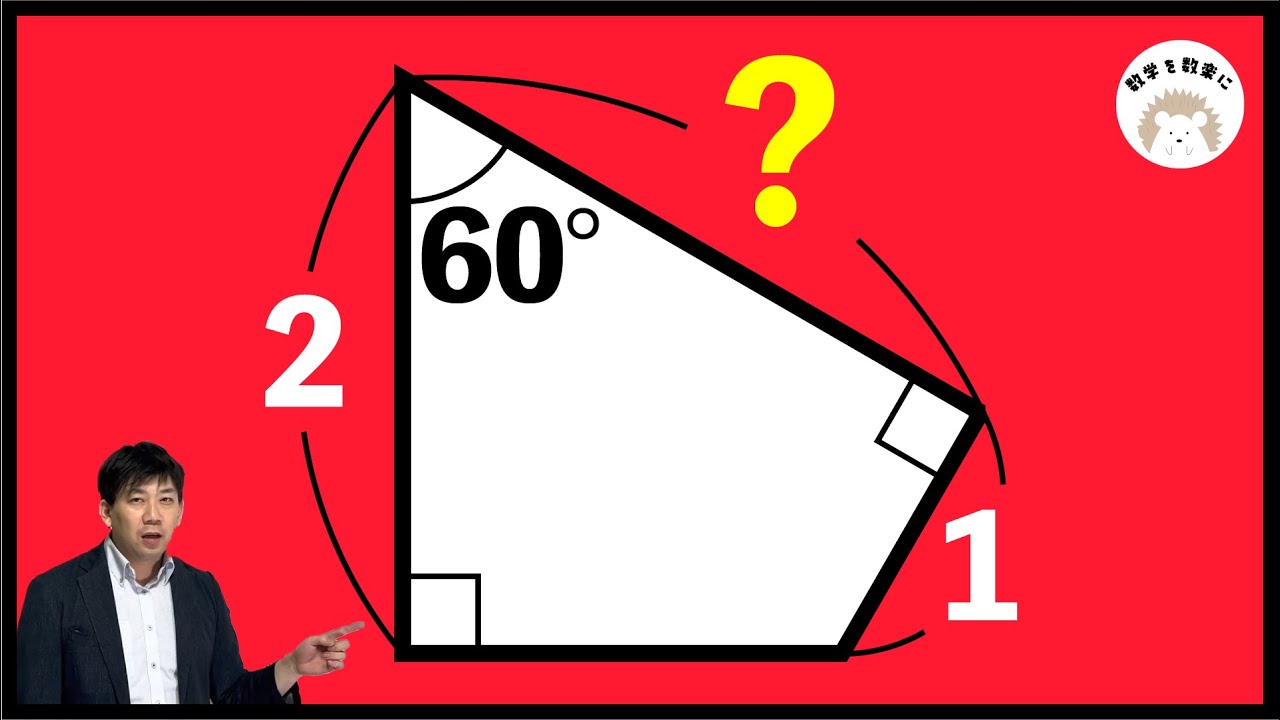
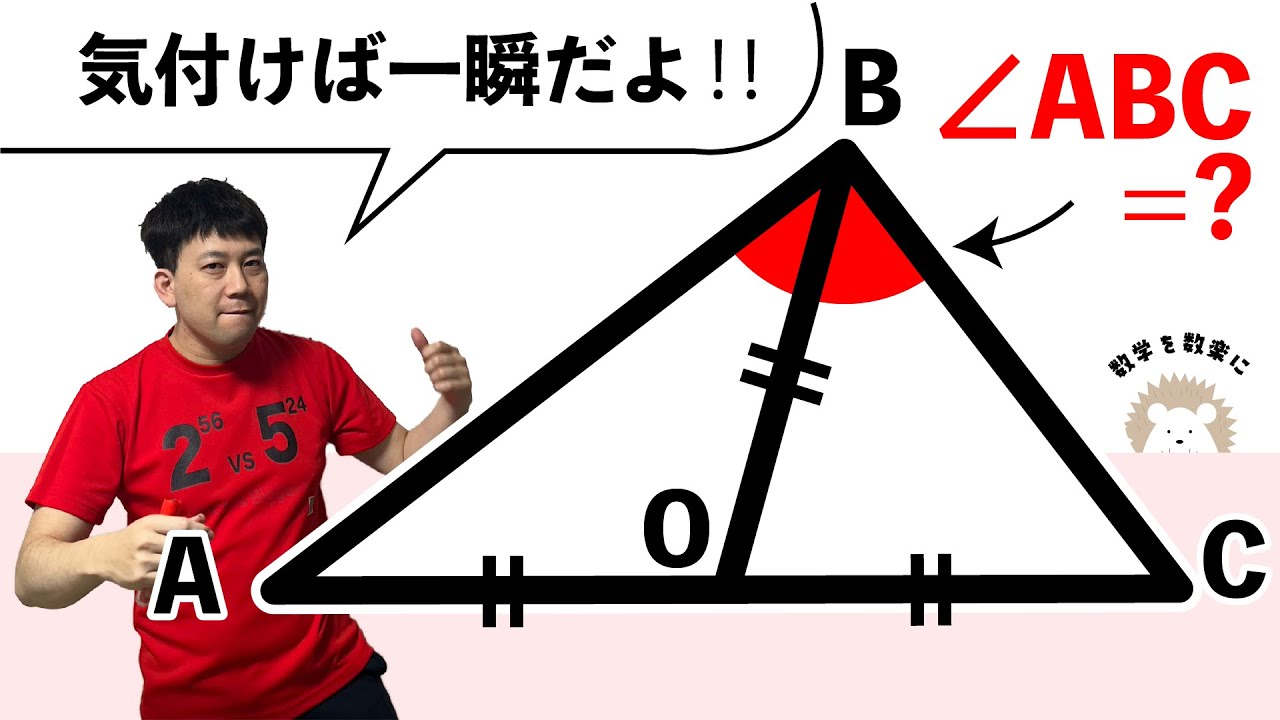
角度を求めよ
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle OAB = \angle OBA = \angle ACB$
$\angle AOB = ?$
*図は動画内参照
この動画を見る
$\angle OAB = \angle OBA = \angle ACB$
$\angle AOB = ?$
*図は動画内参照
福田の数学〜大阪大学2023年理系第5問〜確率漸化式と整数の性質

単元:
#数A#大学入試過去問(数学)#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 1個のさいころをn回投げて、k回目に出た目を$a_k$とする。$b_n$を
$b_n$=$\displaystyle\sum_{k=1}^na_1^{n-k}a_k$
により定義し、b_nが7の倍数とする確率を$p_n$とする。
(1)$p_1$, $p_2$を求めよ。
(2)数列$\left\{p_n\right\}$の一般項を求めよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{5}$ 1個のさいころをn回投げて、k回目に出た目を$a_k$とする。$b_n$を
$b_n$=$\displaystyle\sum_{k=1}^na_1^{n-k}a_k$
により定義し、b_nが7の倍数とする確率を$p_n$とする。
(1)$p_1$, $p_2$を求めよ。
(2)数列$\left\{p_n\right\}$の一般項を求めよ。
2023大阪大学理系過去問
素因数分解せよ!prime factorization

【解答の流れは思い浮かぶか】整数:大阪星光学院高等学校~全国入試問題解法
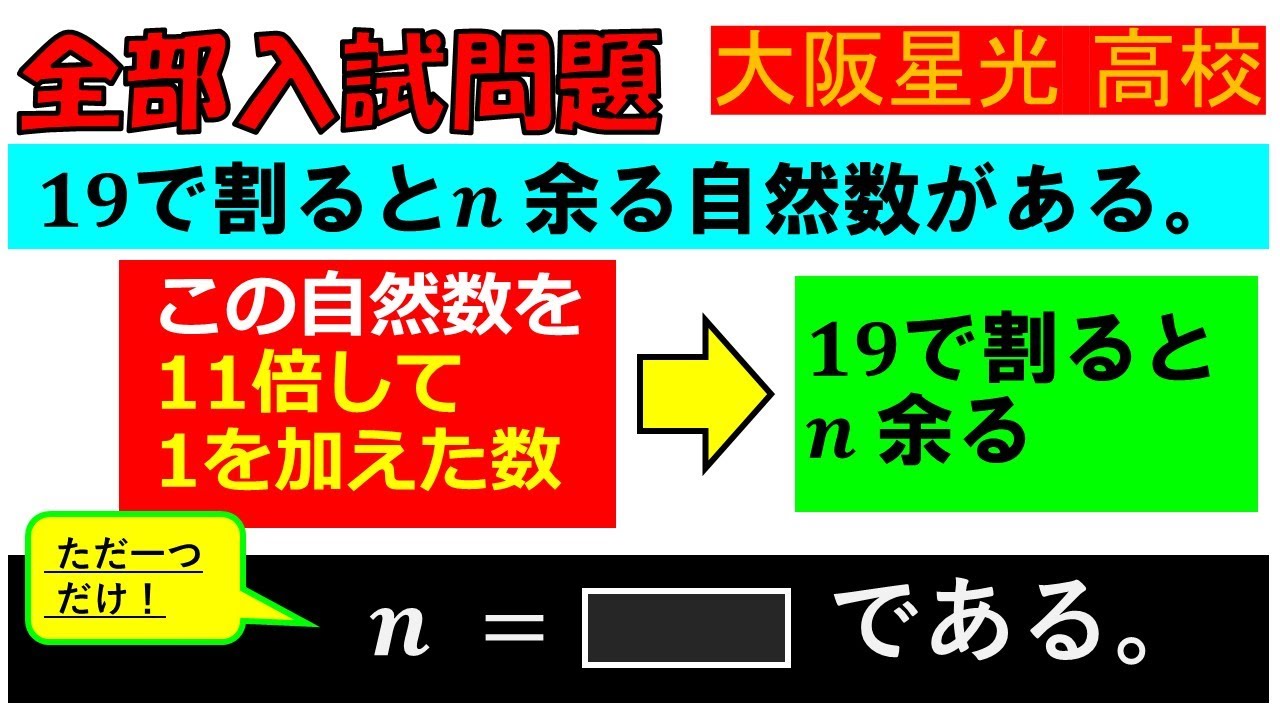
単元:
#数学(中学生)#数A#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
19で割るとn余る自然数がある.
この自然数を11倍して1加えた数も19で割るとn余る.
nはいくつか?
大阪星光学院高等学校過去問
この動画を見る
19で割るとn余る自然数がある.
この自然数を11倍して1加えた数も19で割るとn余る.
nはいくつか?
大阪星光学院高等学校過去問
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数(m,n)をすべて求めよ.
$3・2^n+1=m^2$
この動画を見る
自然数(m,n)をすべて求めよ.
$3・2^n+1=m^2$
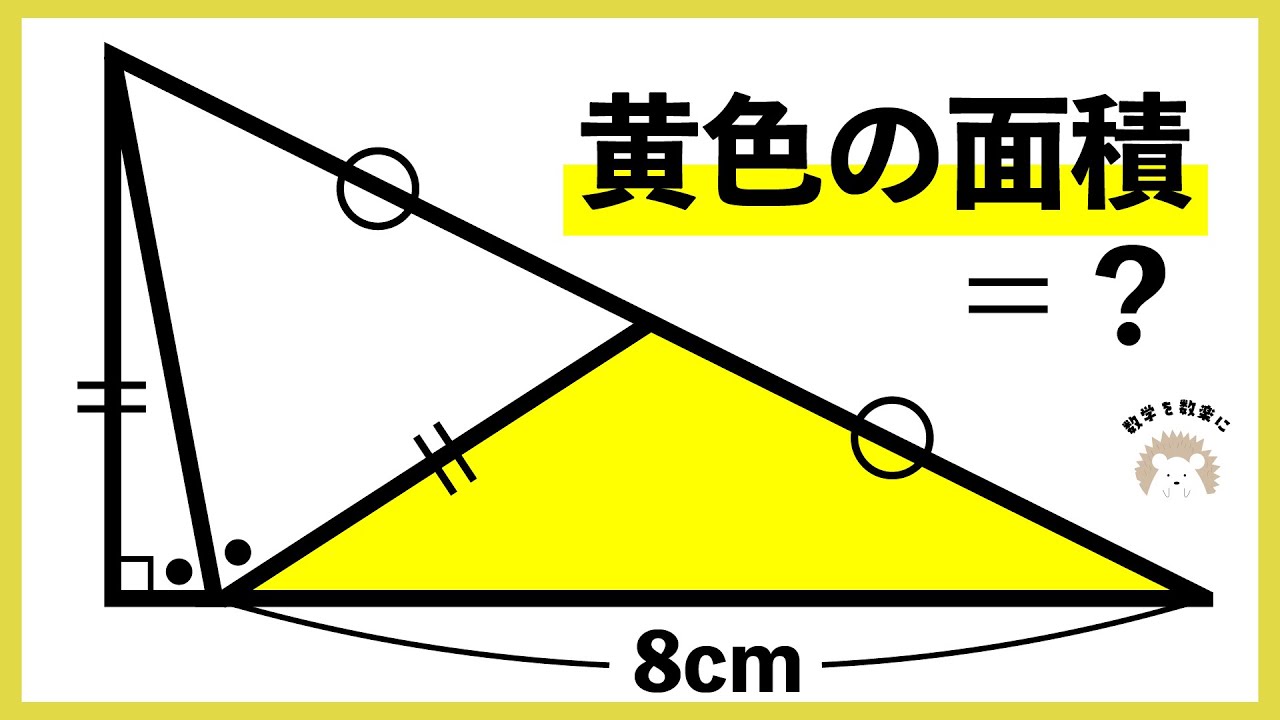
黄色の面積=❓
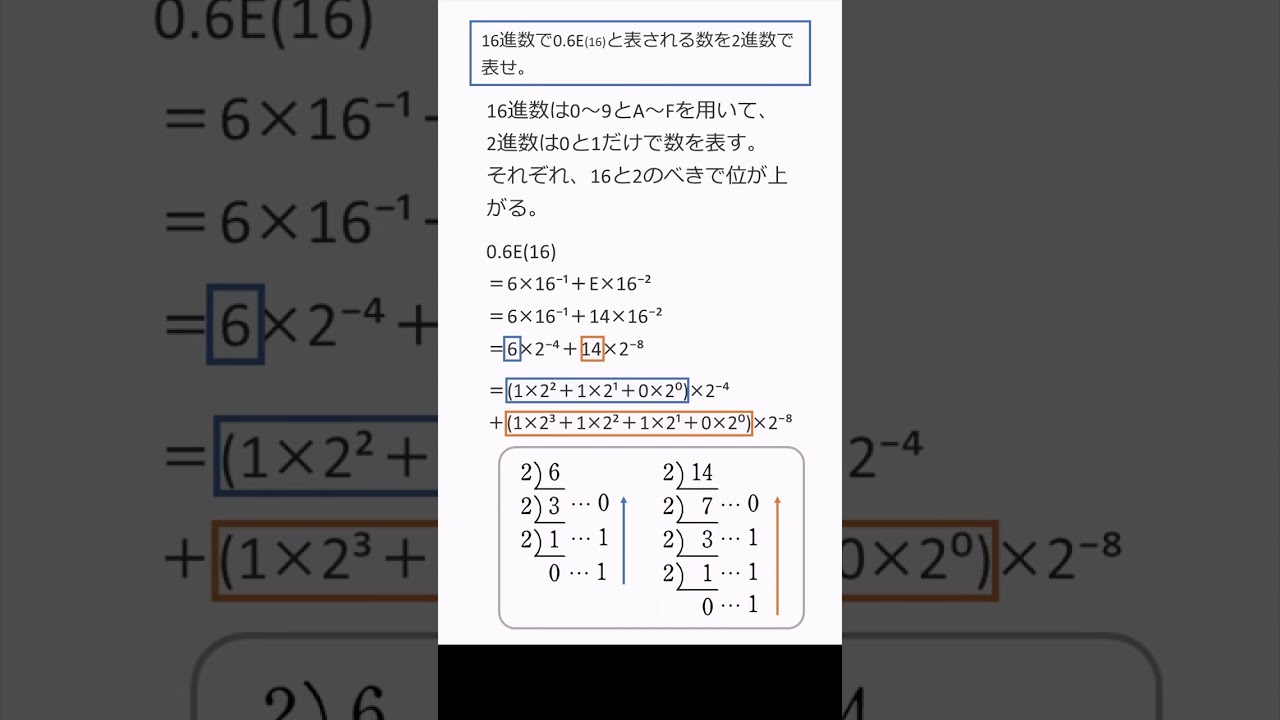
080 16進数0.6Eを2進数に変換しよう!:2のべきの和を使ってスマートに求める! #shorts
きょ、京大!?絶対に落としてはいけない2023年度の確率の問題【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を自然数とする。一個のさいころを$n$回投げ、出た目を順に$X_{1},X_{2}……,X_{n}$とし、$n$個の数の積$X_{1},X_{2}……,X_{n}$を$Y$とする。
(1)$Y$が5で割り切れる確率を求めよ。
京都大過去問
この動画を見る
$n$を自然数とする。一個のさいころを$n$回投げ、出た目を順に$X_{1},X_{2}……,X_{n}$とし、$n$個の数の積$X_{1},X_{2}……,X_{n}$を$Y$とする。
(1)$Y$が5で割り切れる確率を求めよ。
京都大過去問
整数問題 桃山学院

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
m,nは自然数
$4m^2+n^2 = 200 $を満たすmnの値を全て求めよ。
桃山学院高等学校
この動画を見る
m,nは自然数
$4m^2+n^2 = 200 $を満たすmnの値を全て求めよ。
桃山学院高等学校
互いに素の定義は?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数a,bが互いに素なら,$a-b$と$b$も互いに素であることを示せ.$(a \gt b)$
この動画を見る
自然数a,bが互いに素なら,$a-b$と$b$も互いに素であることを示せ.$(a \gt b)$
079 小数点以下の10進数を2進数に変換する方法:2倍して何を求めているのか理解しよう! #shorts
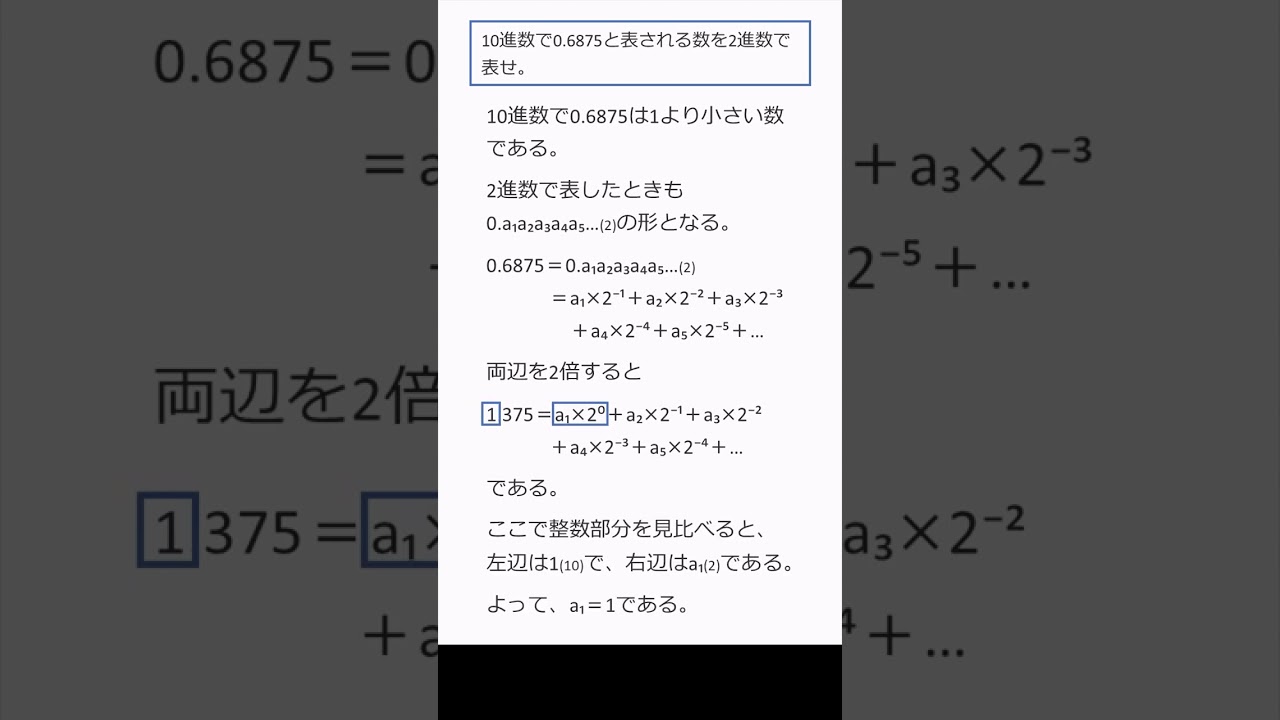
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
10進数で0.6875と表される数を2進数で表せ.
この動画を見る
10進数で0.6875と表される数を2進数で表せ.
気付けば一瞬!!平行四辺形
福田の数学〜東京慈恵会医科大学2023年医学部第3問〜無理数である証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ Oを原点とする座標平面において、第1象限に属する点P($\sqrt 2r$, $\sqrt 3s$)(r,sは有理数)をとるとき、線分OPの長さは無理数となることを示せ。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{3}$ Oを原点とする座標平面において、第1象限に属する点P($\sqrt 2r$, $\sqrt 3s$)(r,sは有理数)をとるとき、線分OPの長さは無理数となることを示せ。
2023東京慈恵会医科大学医学部過去問
数字を規則的に並べるだけで平方数ができる定理を発見したぜ

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$111…11 555…56は平方数であることを示せ.$
この動画を見る
$111…11 555…56は平方数であることを示せ.$
078 2進数の小数も2のべきで分解!:整数と同じ発想で10進数に変換しよう!#shorts
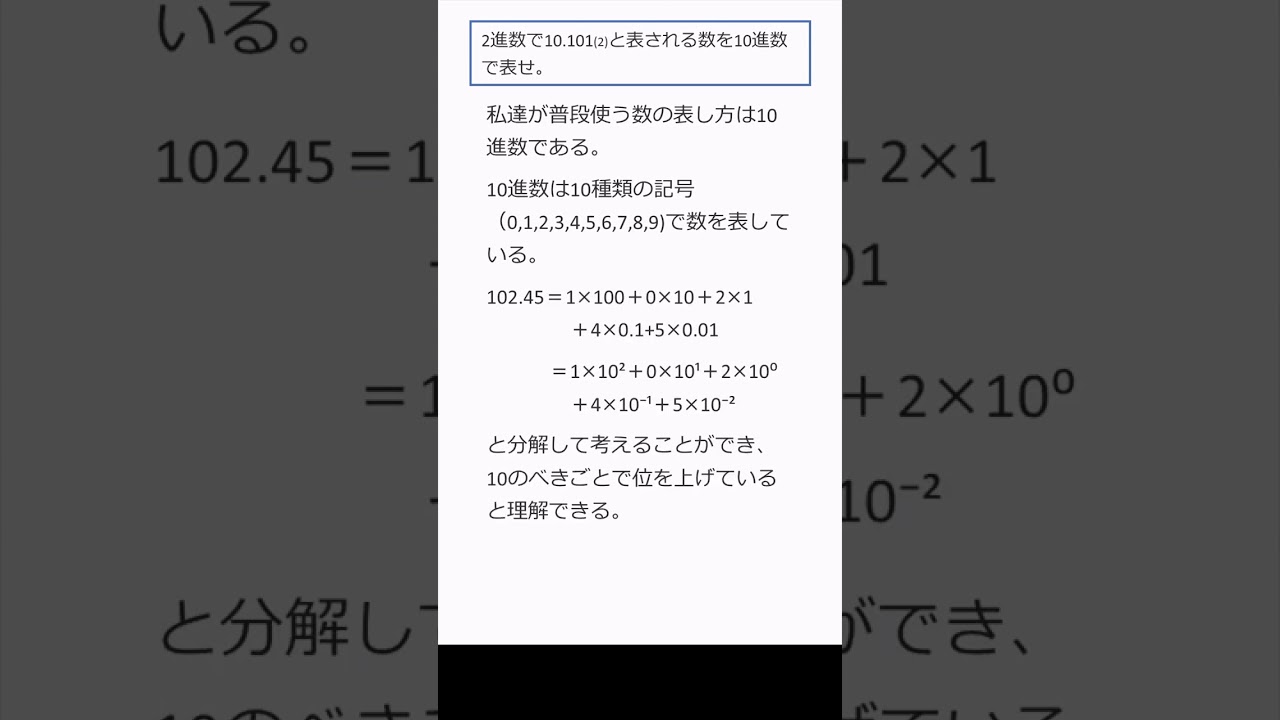
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
二進数で10,101と表される数を10進数で表せ.
この動画を見る
二進数で10,101と表される数を10進数で表せ.
指数方程式
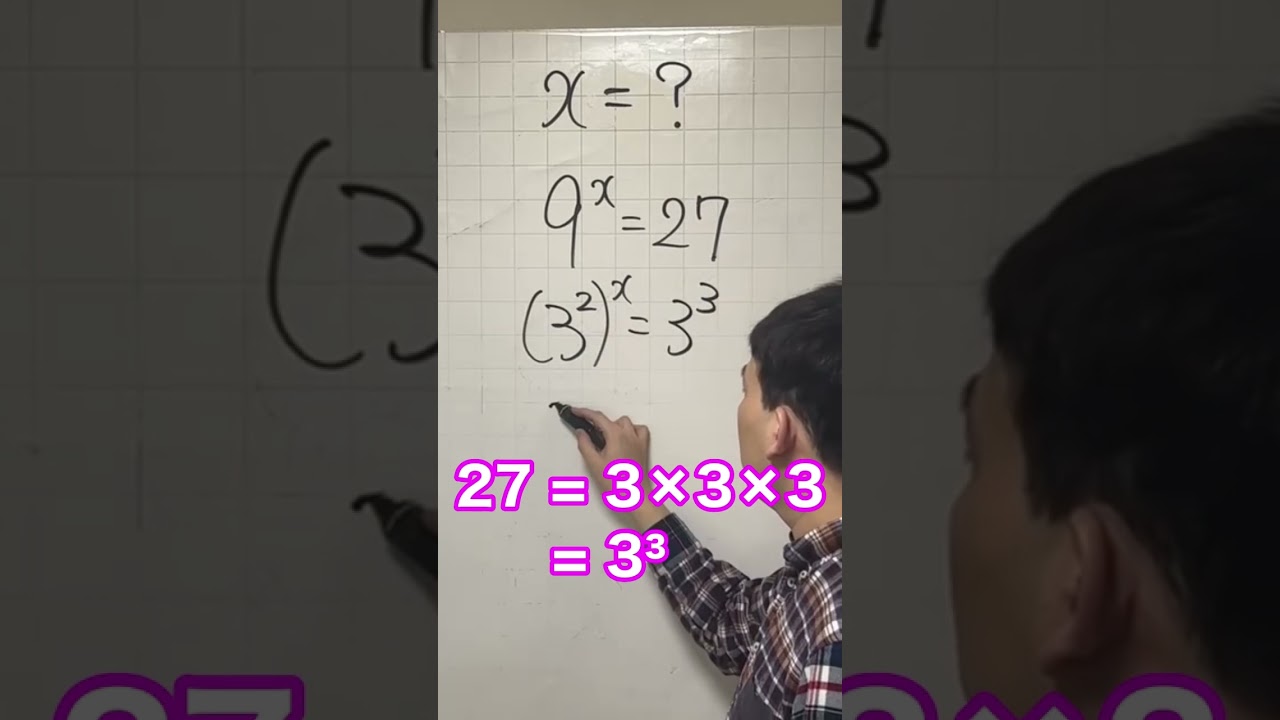
円と正方形 良問です たくさんの別解はコメント欄に いつもありがとうございます。

