 解と判別式・解と係数の関係
解と判別式・解と係数の関係
 解と判別式・解と係数の関係
解と判別式・解と係数の関係
福田の1日1題わかった数学〜高校2年生第2回〜高次方程式と整数解

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
3次方程式$x^3-7x+n=0$ が
3つの整数解をもつように、
$n$の値を定めよ。
この動画を見る
数学$\textrm{II}$ 高次方程式
3次方程式$x^3-7x+n=0$ が
3つの整数解をもつように、
$n$の値を定めよ。
福田の1日1題わかった数学〜高校2年生第1回〜高次方程式

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
3次方程式$x^3+ax+b=0$の
3つの解を$\alpha,\beta,\gamma$とし、
$t_n=\alpha^n+\beta^n+\gamma^n$
のとき、$at_5+bt_4$を$a,b$で表せ。
この動画を見る
数学$\textrm{II}$ 高次方程式
3次方程式$x^3+ax+b=0$の
3つの解を$\alpha,\beta,\gamma$とし、
$t_n=\alpha^n+\beta^n+\gamma^n$
のとき、$at_5+bt_4$を$a,b$で表せ。
練習問題20 教採問題集 指数

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#解と判別式・解と係数の関係#指数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$2^{3x}-2^{2n+2}-3・2^x+12=b$が
負の解をもつように$b$の値の範囲を求めよ.
この動画を見る
$2^{3x}-2^{2n+2}-3・2^x+12=b$が
負の解をもつように$b$の値の範囲を求めよ.
数学「大学入試良問集」【2−1 解と係数の関係】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
3方程式 $x^3-2x^2+3x-4=0$の3つの解を複素数の範囲で考え、それらを$\alpha,\beta,\gamma$とする。
以下の問いに答えよ。
(1)$\alpha^4+\beta^4+\gamma^4$の値を求めよ。
(2)$\alpha^5+\beta^5+\gamma^5$の値を求めよ。
この動画を見る
3方程式 $x^3-2x^2+3x-4=0$の3つの解を複素数の範囲で考え、それらを$\alpha,\beta,\gamma$とする。
以下の問いに答えよ。
(1)$\alpha^4+\beta^4+\gamma^4$の値を求めよ。
(2)$\alpha^5+\beta^5+\gamma^5$の値を求めよ。
練習問題18 どっかの教採の問題

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$f(\theta)=\sin2\theta+\sin\theta-\cos\theta+k\ (0\leqq \theta\leqq \pi)$
$f(\theta)=0$が異なる3つの解をもつような$k$の範囲を求めよ.
この動画を見る
$f(\theta)=\sin2\theta+\sin\theta-\cos\theta+k\ (0\leqq \theta\leqq \pi)$
$f(\theta)=0$が異なる3つの解をもつような$k$の範囲を求めよ.
解の公式の利用 A 2021専大松戸
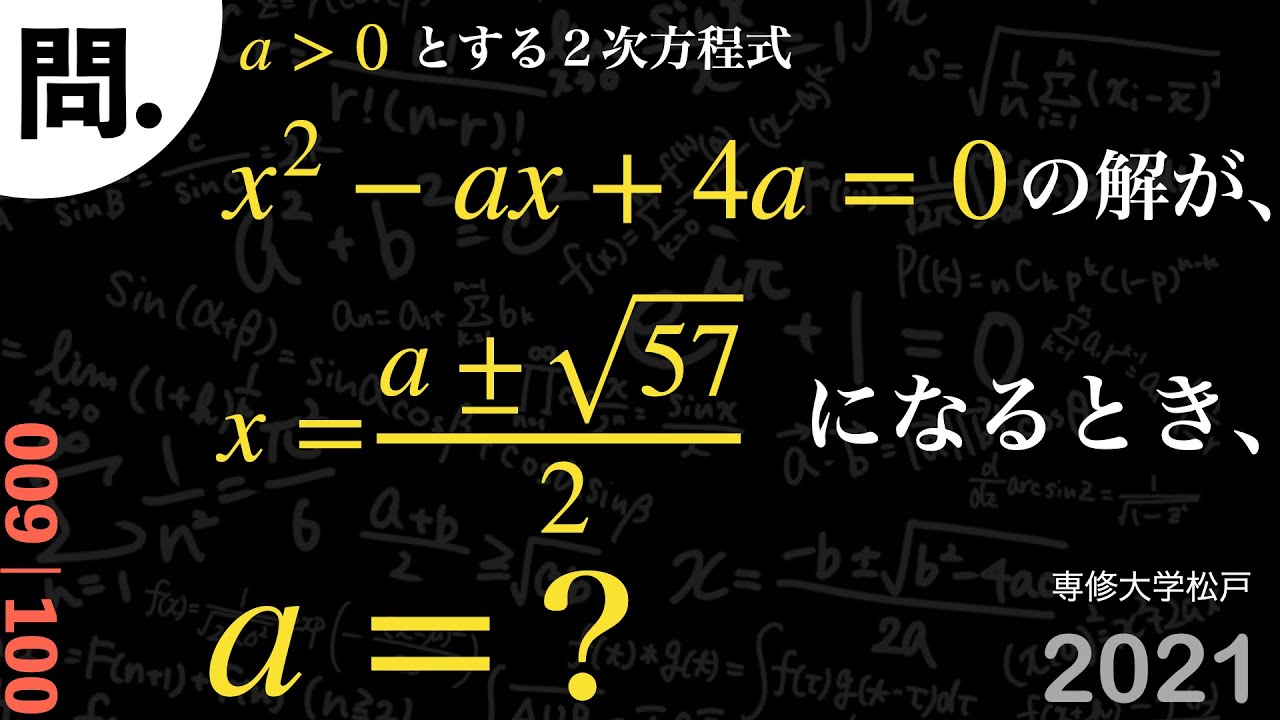
単元:
#数学(中学生)#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a>0とする2次方程式
$x^2-ax+4a=0$の解が
$x=\frac{a ± \sqrt{57} }{2}$となるとき
a=?(a>0)
2021専修大学松戸高等学校
この動画を見る
a>0とする2次方程式
$x^2-ax+4a=0$の解が
$x=\frac{a ± \sqrt{57} }{2}$となるとき
a=?(a>0)
2021専修大学松戸高等学校
【数Ⅱ】複素数と方程式:2x²-6x-3=0の解がα、βのとき、①β²/α+α²/β②(2α²-6α-5)(2β²-6β-1)の値を求めよ。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$2x^2-6x-3=0$の解が$\alpha,\beta$のとき、
①$\dfrac{\beta^2}{\alpha}+\dfrac{\alpha^2}{\beta}
②$(2\alpha^2-6\alpha-5)(2\beta^2-6\beta-1)$の値を求めよ。
この動画を見る
$2x^2-6x-3=0$の解が$\alpha,\beta$のとき、
①$\dfrac{\beta^2}{\alpha}+\dfrac{\alpha^2}{\beta}
②$(2\alpha^2-6\alpha-5)(2\beta^2-6\beta-1)$の値を求めよ。
【数Ⅱ】複素数と方程式:3次方程式x³-x²+2x-3=0の3つの解をα,β,γとするとき、次の式の値を求めよう。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3次方程式$x^3-x^2+2x-3=0$の3つの解を$\alpha,\beta,y$とするとき、次の式の値を求めよう。
(1)$\alpha^2+\beta^2+y^2$
(2)$\alpha^3+\beta^3+y^3$
(3)$\dfrac{1}{\alpha}+\dfrac{1}{\beta}+\dfrac{1}{y}$
(4)$(1-\alpha)(1-\beta)(1-y)$
この動画を見る
3次方程式$x^3-x^2+2x-3=0$の3つの解を$\alpha,\beta,y$とするとき、次の式の値を求めよう。
(1)$\alpha^2+\beta^2+y^2$
(2)$\alpha^3+\beta^3+y^3$
(3)$\dfrac{1}{\alpha}+\dfrac{1}{\beta}+\dfrac{1}{y}$
(4)$(1-\alpha)(1-\beta)(1-y)$
数検準1級1次過去問(2番 解と係数の関係)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣$x^3-7x^2-4x+1=0$
の3つの解をα、β、γとする。
$α^2+β^2+γ^2$の値を求めよ。
解と係数の関係
$ax^3+bx^2+cx+d=0$
$α+β+γ=- \frac{b}{a}$
$αβ+βγ+γα=\frac{c}{a}$
$αβγ=- \frac{d}{a}$
この動画を見る
2⃣$x^3-7x^2-4x+1=0$
の3つの解をα、β、γとする。
$α^2+β^2+γ^2$の値を求めよ。
解と係数の関係
$ax^3+bx^2+cx+d=0$
$α+β+γ=- \frac{b}{a}$
$αβ+βγ+γα=\frac{c}{a}$
$αβγ=- \frac{d}{a}$
10東京都教員採用試験(数学:1-(1) 解と係数の関係)

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣$2x^2-3x+2=0$の2つの解をα、βとする。
$α+\frac{1}{β}$,$β+\frac{1}{α}$を解にもつ$x^2$の係数が1となる2次方程式を求めよ。
この動画を見る
1⃣$2x^2-3x+2=0$の2つの解をα、βとする。
$α+\frac{1}{β}$,$β+\frac{1}{α}$を解にもつ$x^2$の係数が1となる2次方程式を求めよ。
【難問解説】「解と係数の関係」と「判別式」を利用した最大・最小問題【半分 for you 動画】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
「解と係数の関係」と「判別式」を利用した最大・最小問題
-----------------
実数$x、y、z$は$x+y+z=0,x^2-x-1=yz$を満たす。
$x^3+y^3+z^3$のn最大値・最小値と、そのときの$x$の値を求めよ。
この動画を見る
「解と係数の関係」と「判別式」を利用した最大・最小問題
-----------------
実数$x、y、z$は$x+y+z=0,x^2-x-1=yz$を満たす。
$x^3+y^3+z^3$のn最大値・最小値と、そのときの$x$の値を求めよ。
18神奈川県教員採用試験(数学:6番 解と係数の関係)

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
6⃣$x^3+kx^2+2x+10=0$の解がx=-2、α、βのとき、$α^2+β^2$の値を求めよ。
この動画を見る
6⃣$x^3+kx^2+2x+10=0$の解がx=-2、α、βのとき、$α^2+β^2$の値を求めよ。
17神奈川県教員採用試験(数学:8番 積分【面積の最小値】)

単元:
#数Ⅱ#2次関数#複素数と方程式#2次関数とグラフ#微分法と積分法#解と判別式・解と係数の関係#面積、体積#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
8⃣$y=x^2$と(-1,3)を通る直線lで囲まれた面積Sの最小値を求めよ。
この動画を見る
8⃣$y=x^2$と(-1,3)を通る直線lで囲まれた面積Sの最小値を求めよ。
14兵庫県教員採用試験(数学:1-5番 解と係数の関係)

単元:
#数Ⅰ#数Ⅱ#複素数と方程式#図形と計量#三角比(三角比・拡張・相互関係・単位円)#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(5)
$8x^2+kx-3=0,x=sinθ,cosθ$のときkの値を求めよ。
この動画を見る
1⃣-(5)
$8x^2+kx-3=0,x=sinθ,cosθ$のときkの値を求めよ。
18東京都教員採用試験(数学:解と係数の関係)
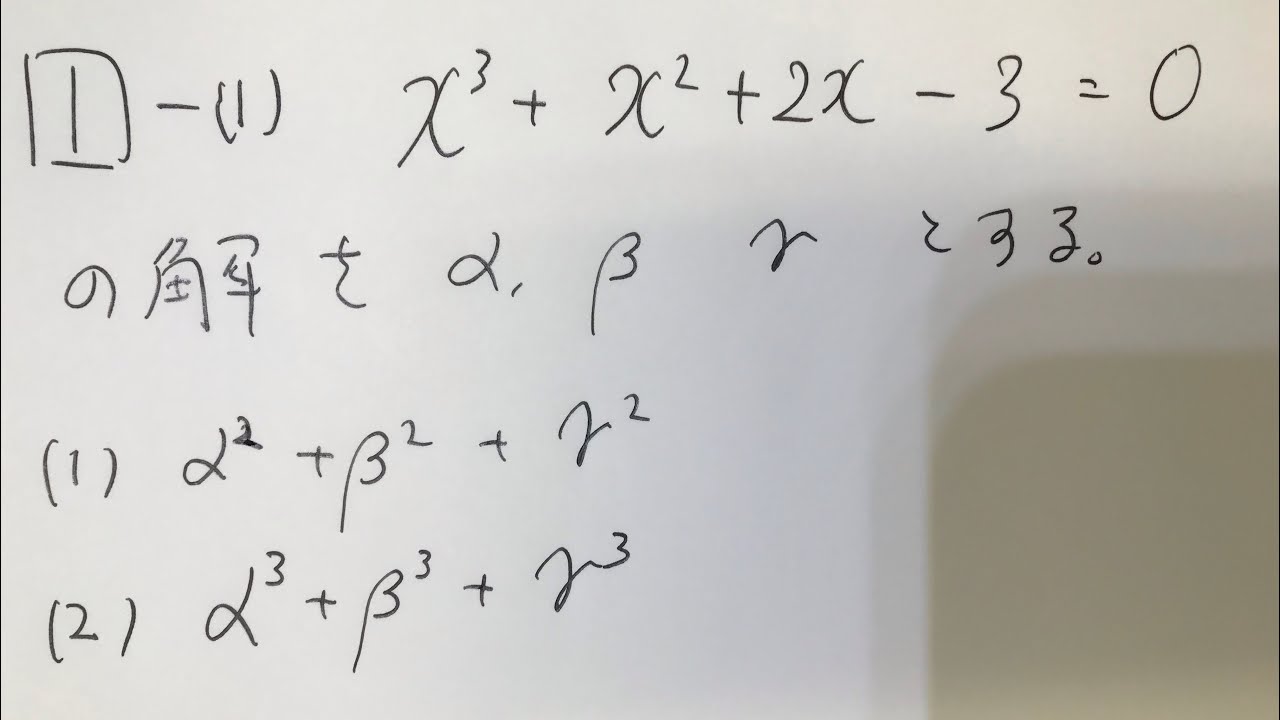
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$x^3+x^2+2x-3=0$の解をα、β、γとする。
(1)$α^2+β^2+γ^2$
(2)$α^3+β^3+γ^3$
この動画を見る
1⃣-(1)
$x^3+x^2+2x-3=0$の解をα、β、γとする。
(1)$α^2+β^2+γ^2$
(2)$α^3+β^3+γ^3$
【数Ⅱ】複素数と方程式:3次方程式が異なる3つの解を持つ条件:方程式x³+(a-1)x-a=0が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#ニュースコープ#ニュースコープ数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$x^3+(a-1)x-a=0$が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。
この動画を見る
方程式$x^3+(a-1)x-a=0$が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。
式の値
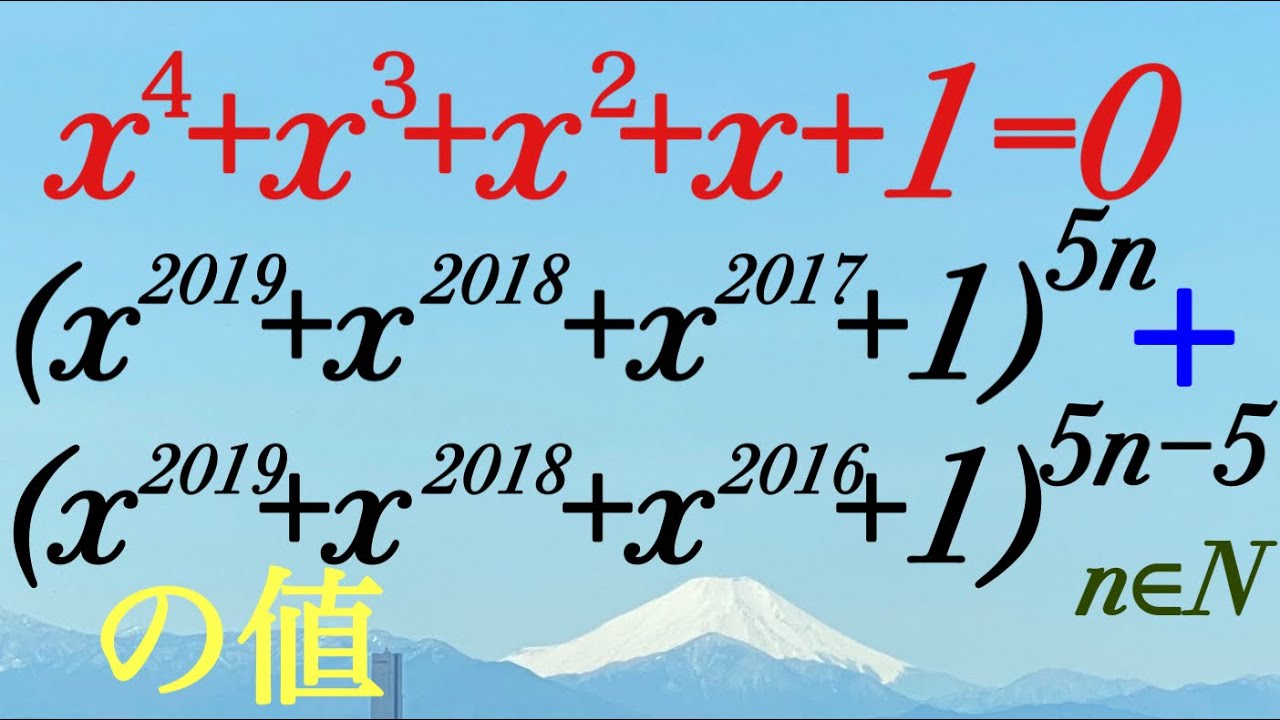
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^4+x^3+x^2+x+1=0$を満たすとき,
$(x^{2019}+x^{2018}+x^{2017}+1)^{5n}+$
$(x^{2019}+x^{2018}+x^{2016}+1)^{5n-5}$の値を求めよ.
この動画を見る
$x^4+x^3+x^2+x+1=0$を満たすとき,
$(x^{2019}+x^{2018}+x^{2017}+1)^{5n}+$
$(x^{2019}+x^{2018}+x^{2016}+1)^{5n-5}$の値を求めよ.
光文社新書「中学の知識でオイラー公式がわかる」Vol14

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2=9$
$(x-2)^2=25$
$x^2=5$
$(x+3)^2=2$
この動画を見る
$x^2=9$
$(x-2)^2=25$
$x^2=5$
$(x+3)^2=2$
横浜市立(医)3項間漸化式 良問再投稿

単元:
#数Ⅱ#大学入試過去問(数学)#解と判別式・解と係数の関係#数列#漸化式#数学(高校生)#数B#横浜市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=a_2=1$ 一般項を求めよ
$a_{n+2}-5a_{n+1}+6a_n-6n=0$
出典:2016年横浜市立大学 医学部 過去問
この動画を見る
$a_1=a_2=1$ 一般項を求めよ
$a_{n+2}-5a_{n+1}+6a_n-6n=0$
出典:2016年横浜市立大学 医学部 過去問
防衛医大 複素数の計算

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)#防衛医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\displaystyle \frac{1+\sqrt{ 3 }i}{2},\beta=\displaystyle \frac{1-\sqrt{ 3 }i}{2}$
$\gamma=\displaystyle \frac{\beta^2-4\beta +3}{\alpha^{n+2}-\alpha^{n+1}+\alpha^{n}+\alpha^{3}-2\alpha^{2}+5\alpha-2}$
$\gamma^3$の値を求めよ
出典:2011年防衛医科大学校 過去問
この動画を見る
$\alpha=\displaystyle \frac{1+\sqrt{ 3 }i}{2},\beta=\displaystyle \frac{1-\sqrt{ 3 }i}{2}$
$\gamma=\displaystyle \frac{\beta^2-4\beta +3}{\alpha^{n+2}-\alpha^{n+1}+\alpha^{n}+\alpha^{3}-2\alpha^{2}+5\alpha-2}$
$\gamma^3$の値を求めよ
出典:2011年防衛医科大学校 過去問
お茶の水女子大 解答に誤りがあるので、訂正版を出しました。素晴らしい別解をコメントくださった方がいるので公開はしておきます。

単元:
#大学入試過去問(数学)#2次関数#複素数と方程式#2次関数とグラフ#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a \neq 1$
$3(a-1)x^2+6x-a-2=0$は0と1の間に少なくとも1つの解をもつことを示せ
出典:お茶の水女子大学 過去問訂正版
この動画を見る
$a \neq 1$
$3(a-1)x^2+6x-a-2=0$は0と1の間に少なくとも1つの解をもつことを示せ
出典:お茶の水女子大学 過去問訂正版
東北大 3次方程式 整数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3-(p-3)x^2-3x+p-1=0$の3つの解がすべて整数となるような実数$p$を求めよ
出典:2000年東北大学 過去問
この動画を見る
$x^3-(p-3)x^2-3x+p-1=0$の3つの解がすべて整数となるような実数$p$を求めよ
出典:2000年東北大学 過去問
【数Ⅱ】複素数と方程式:2次方程式の解の判別(最高次数の係数が文字の場合)kは定数とする。次の方程式の解の種類を判別せよ。(k²-1)x²+2(k-1)+2=0

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$(k²-1)x²+2(k-1)+2=0$の解の種類を判別せよ。
この動画を見る
$(k²-1)x²+2(k-1)+2=0$の解の種類を判別せよ。
神戸大 虚数解を持つ3次方程式 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+ax^2+bx+c=0$
$a,b,c$は整数
1つの解は$\displaystyle \frac{3+\sqrt{ 7 }i}{2}$
$0 \leqq x \leqq 1$に1つの実数解をもつ$(a,b,c)$の組すべて求めよ
出典:神戸大学 過去問
この動画を見る
$x^3+ax^2+bx+c=0$
$a,b,c$は整数
1つの解は$\displaystyle \frac{3+\sqrt{ 7 }i}{2}$
$0 \leqq x \leqq 1$に1つの実数解をもつ$(a,b,c)$の組すべて求めよ
出典:神戸大学 過去問
名古屋大 根号の計算 4次方程式 Mathematics Japanese university entrance exam

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$(\sqrt{ 9+2\sqrt{ 17 } }+\sqrt{ 9-2\sqrt{ 17 } })^2$を計算せよ
(2)
$a=\sqrt{ 13 }+\sqrt{ 9+2\sqrt{ 17 } }+\sqrt{ 9-2\sqrt{ 17 } }$を解にもつ整数係数の4次方程式を求めよ
(3)
8つの実数$\pm \sqrt{ 13 }\pm \sqrt{ 9+2\sqrt{ 17 } } \pm \sqrt{ 9-2\sqrt{ 17 } }$(複号任意)のうち(2)で求めた方程式の解
出典:1975年名古屋大学 過去問
この動画を見る
(1)
$(\sqrt{ 9+2\sqrt{ 17 } }+\sqrt{ 9-2\sqrt{ 17 } })^2$を計算せよ
(2)
$a=\sqrt{ 13 }+\sqrt{ 9+2\sqrt{ 17 } }+\sqrt{ 9-2\sqrt{ 17 } }$を解にもつ整数係数の4次方程式を求めよ
(3)
8つの実数$\pm \sqrt{ 13 }\pm \sqrt{ 9+2\sqrt{ 17 } } \pm \sqrt{ 9-2\sqrt{ 17 } }$(複号任意)のうち(2)で求めた方程式の解
出典:1975年名古屋大学 過去問
京都大 4次方程式の解の個数 Mathematics Japanese university entrance exam Kyoto University

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x^2+ax+1)(3x^2+ax-3)=0$
この方程式の実数解の個数は?
出典:2008年京都大学 過去問
この動画を見る
$(x^2+ax+1)(3x^2+ax-3)=0$
この方程式の実数解の個数は?
出典:2008年京都大学 過去問
東京理科大 3次方程式 解と係数 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
09年 東京理科大学
$x^3-2x^2+x+5=0$の3つの解を$a,b,c$とする。次の値を求めよ。
(1)$a^3+b^3+c^3$
(2)$a^4+b^4+c^4$
この動画を見る
09年 東京理科大学
$x^3-2x^2+x+5=0$の3つの解を$a,b,c$とする。次の値を求めよ。
(1)$a^3+b^3+c^3$
(2)$a^4+b^4+c^4$
京都大 4次方程式 虚数解 Mathematics Japanese university entrance exam Kyoto University

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
国立大学法人京都大学
$0°\leqqθ\lt90°$ $x$の4次方程式
$\{x^2-2(cosθ)x-cosθ+1\}×$
$\{x^2+2(tanθ)x+3\}=0$
は虚数解を少なくとも1つ持つことを示せ
この動画を見る
国立大学法人京都大学
$0°\leqqθ\lt90°$ $x$の4次方程式
$\{x^2-2(cosθ)x-cosθ+1\}×$
$\{x^2+2(tanθ)x+3\}=0$
は虚数解を少なくとも1つ持つことを示せ
茨城大 Mathematics Japanese university entrance exam

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
茨城大学過去問題
$n \geqq 2$ 整数
(x+1)(x+2)(x+3)・・・(x+n)
(1)$x^{n-1}$の係数
(2)$x^{n-2}$の係数
この動画を見る
茨城大学過去問題
$n \geqq 2$ 整数
(x+1)(x+2)(x+3)・・・(x+n)
(1)$x^{n-1}$の係数
(2)$x^{n-2}$の係数
学習院大 三次方程式と複素数 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#複素数と方程式#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
'04学習院大学過去問題
a実数
$f(x)=4x^3-4ax^2+(a^2+3)x+a^2+4a+7$
(1)任意のaについてf(m)=0が成り立つ実数m
(2)f(x)=0の3つの解を複素数平面上に図示したとき、それらが正三角形になるようなaの値
この動画を見る
'04学習院大学過去問題
a実数
$f(x)=4x^3-4ax^2+(a^2+3)x+a^2+4a+7$
(1)任意のaについてf(m)=0が成り立つ実数m
(2)f(x)=0の3つの解を複素数平面上に図示したとき、それらが正三角形になるようなaの値
