複素数と方程式
複素数と方程式
【数Ⅱ】【複素数と方程式】2次方程式の解と判別式1 ※問題文は概要欄
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#複素数と方程式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の2次方程式を解け。
(1)$3(x+1)^2-2(x+1)-1=0$
(2)$2(x-1)^2-4(x-1)+3=0$
(3)$x^2-\sqrt{2} x+\sqrt{2} -1=0$
(4)$x^2-2x+9+2\sqrt{15}=0$
kは定数とする。次の方程式の解の種類を判別せよ。
(1)$kx^2-3x+1=0$
(2)$(k^2-1) x^2+2(k-1)+2=0$
この動画を見る
次の2次方程式を解け。
(1)$3(x+1)^2-2(x+1)-1=0$
(2)$2(x-1)^2-4(x-1)+3=0$
(3)$x^2-\sqrt{2} x+\sqrt{2} -1=0$
(4)$x^2-2x+9+2\sqrt{15}=0$
kは定数とする。次の方程式の解の種類を判別せよ。
(1)$kx^2-3x+1=0$
(2)$(k^2-1) x^2+2(k-1)+2=0$
【数Ⅱ】【複素数と方程式】複素数の純虚数、共役 ※問題文は概要欄
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#複素数と方程式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの複素数a+biと2-3iの和が純虚数、積が実数となるように、実数a, bの値を定めよ。
虚数α、βの和、積がともに実数ならば、α、βは互いに共役であることを示せ。
この動画を見る
2つの複素数a+biと2-3iの和が純虚数、積が実数となるように、実数a, bの値を定めよ。
虚数α、βの和、積がともに実数ならば、α、βは互いに共役であることを示せ。
【数Ⅱ】【複素数と方程式】複素数基本 ※問題文は概要欄
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#複素数と方程式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1)$\left({\displaystyle \frac{3-2i}{2+3i}}\right)^2$
(2)$\left({\displaystyle \frac{-1+\sqrt{3}i}{2}}\right)^2$
(3)$(2+i)^3+(2-i)^3$
(4)$\left(\displaystyle \frac{1}{i}-i\right)\left(\displaystyle \frac{2}{i}+i\right)i^3$
(5)$\displaystyle \frac{2+3i}{3-2i}+\displaystyle \frac{2-3i}{3+2i}$
(6)$\displaystyle \frac{1}{i}+1-i+i²-i³+i⁴$
$x=\displaystyle \frac{-1+\sqrt{5}i}{2}$,$y=\displaystyle \frac{-1-\sqrt{5}i}{2}$であるとき、次の式の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3+x^2y+xy^2$
次の等式を満たす実数x,yの値を求めよ。
(1)$(2i+3)x+(2-3i)y=5-i$
(2)$(1-2i)(x+yi)=2+6i$
(3)$(1+xi)^2+(x+i)^2=0$
(4)$\displaystyle \frac{1}{2+i}+\displaystyle \frac{1}{x+yi}=\displaystyle \frac{1}{2}$
この動画を見る
(1)$\left({\displaystyle \frac{3-2i}{2+3i}}\right)^2$
(2)$\left({\displaystyle \frac{-1+\sqrt{3}i}{2}}\right)^2$
(3)$(2+i)^3+(2-i)^3$
(4)$\left(\displaystyle \frac{1}{i}-i\right)\left(\displaystyle \frac{2}{i}+i\right)i^3$
(5)$\displaystyle \frac{2+3i}{3-2i}+\displaystyle \frac{2-3i}{3+2i}$
(6)$\displaystyle \frac{1}{i}+1-i+i²-i³+i⁴$
$x=\displaystyle \frac{-1+\sqrt{5}i}{2}$,$y=\displaystyle \frac{-1-\sqrt{5}i}{2}$であるとき、次の式の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3+x^2y+xy^2$
次の等式を満たす実数x,yの値を求めよ。
(1)$(2i+3)x+(2-3i)y=5-i$
(2)$(1-2i)(x+yi)=2+6i$
(3)$(1+xi)^2+(x+i)^2=0$
(4)$\displaystyle \frac{1}{2+i}+\displaystyle \frac{1}{x+yi}=\displaystyle \frac{1}{2}$
福田のおもしろ数学382〜整式が素数となる自然数nの値
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n^8+n+1$が素数となる$n$をすべて求めて下さい。
この動画を見る
$n^8+n+1$が素数となる$n$をすべて求めて下さい。
福田のおもしろ数学343〜3次方程式の解の存在範囲
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1 \geq a \geq b \geq c >0$ のとき $x^3+a x^2+bx+c=0$ の1つの解を $\alpha$ とする。
$|a| \leq 1$ を証明してください。
この動画を見る
$1 \geq a \geq b \geq c >0$ のとき $x^3+a x^2+bx+c=0$ の1つの解を $\alpha$ とする。
$|a| \leq 1$ を証明してください。
福田のおもしろ数学306〜5次方程式の5つの解がすべて実数にはなれない条件
単元：
#数Ⅱ#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数係数の5次方程式
$z^5+az^4+bz^3+cz^2+dz+e=0$
について$2a^2\lt 5b$のときはすべての解が実数にはなれないことを示してください。
この動画を見る
実数係数の5次方程式
$z^5+az^4+bz^3+cz^2+dz+e=0$
について$2a^2\lt 5b$のときはすべての解が実数にはなれないことを示してください。
福田のおもしろ数学301〜4次方程式の解と係数の関係
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x ^ 4 - 18x ^ 3 + k x ^ 2 + 200x - 1984 = 0 $の2つの解の積が$-32$のとき、実数$k$の値は?
この動画を見る
$x ^ 4 - 18x ^ 3 + k x ^ 2 + 200x - 1984 = 0 $の2つの解の積が$-32$のとき、実数$k$の値は?
#関西大学2024 #方程式_70
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
この動画を見る
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
福田の数学〜慶應義塾大学2024総合政策学部第1問(1)〜2次方程式の作成
#北海道大学1957#因数分解_64
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
この動画を見る
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
3次不等式を解け
#北海道大学1919#因数分解_63
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2$を因数分解せよ.
1919北海道帝国大学過去問題
この動画を見る
$a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2$を因数分解せよ.
1919北海道帝国大学過去問題
戦後の京都大学の入試いけんじゃね？ 京都大学医学部1946 大学入試問題#929
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^4-17x^2-34x-30=0$
なる方程式を解け.
1946京都大学医学部過去問題
この動画を見る
$x^4-17x^2-34x-30=0$
なる方程式を解け.
1946京都大学医学部過去問題
福田の数学〜明治大学2024理工学部第1問(1)〜高次方程式と整数解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$k,l,m$ を定数とする。関数 $f(x)=4x^3+kx^2-lx+m$ は次の $3$ つの条件を満たすとする。
・ $k,l,m$ は $0$ 以上の整数である。
・ $x$ に関する方程式 $f(x)=0$ は $\frac{1}{2}$ を解にもつ。
・ $f(x)$ を微分して得られる整式を $f'(x)$ とするとき、 $f'(x)$ を $x+2$ で割ったときの余りは $41$ である。
このとき、$k=\fbox{ア},$ $l=\fbox{イ},$ $m=\fbox{ウ}$ であり、方程式 $f(x)=0$ の $\frac{1}{2}$ 以外の解は $\displaystyle -\frac{\fbox{エ}}{\fbox{オ}}$ と $\fbox{カ}$ である。
この動画を見る
$k,l,m$ を定数とする。関数 $f(x)=4x^3+kx^2-lx+m$ は次の $3$ つの条件を満たすとする。
・ $k,l,m$ は $0$ 以上の整数である。
・ $x$ に関する方程式 $f(x)=0$ は $\frac{1}{2}$ を解にもつ。
・ $f(x)$ を微分して得られる整式を $f'(x)$ とするとき、 $f'(x)$ を $x+2$ で割ったときの余りは $41$ である。
このとき、$k=\fbox{ア},$ $l=\fbox{イ},$ $m=\fbox{ウ}$ であり、方程式 $f(x)=0$ の $\frac{1}{2}$ 以外の解は $\displaystyle -\frac{\fbox{エ}}{\fbox{オ}}$ と $\fbox{カ}$ である。
ポイントは実数 摂南大
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x^2-6xy+10y^2-6y+9=0$
$x=? ,y=?$
$(ただしx,yは実数)$
この動画を見る
$x^2-6xy+10y^2-6y+9=0$
$x=? ,y=?$
$(ただしx,yは実数)$
【数学】中高一貫校用問題集数式・関数編：分数式を含む方程式の解法
単元：
#数Ⅱ#複素数と方程式#数学(高校生)
教材：
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
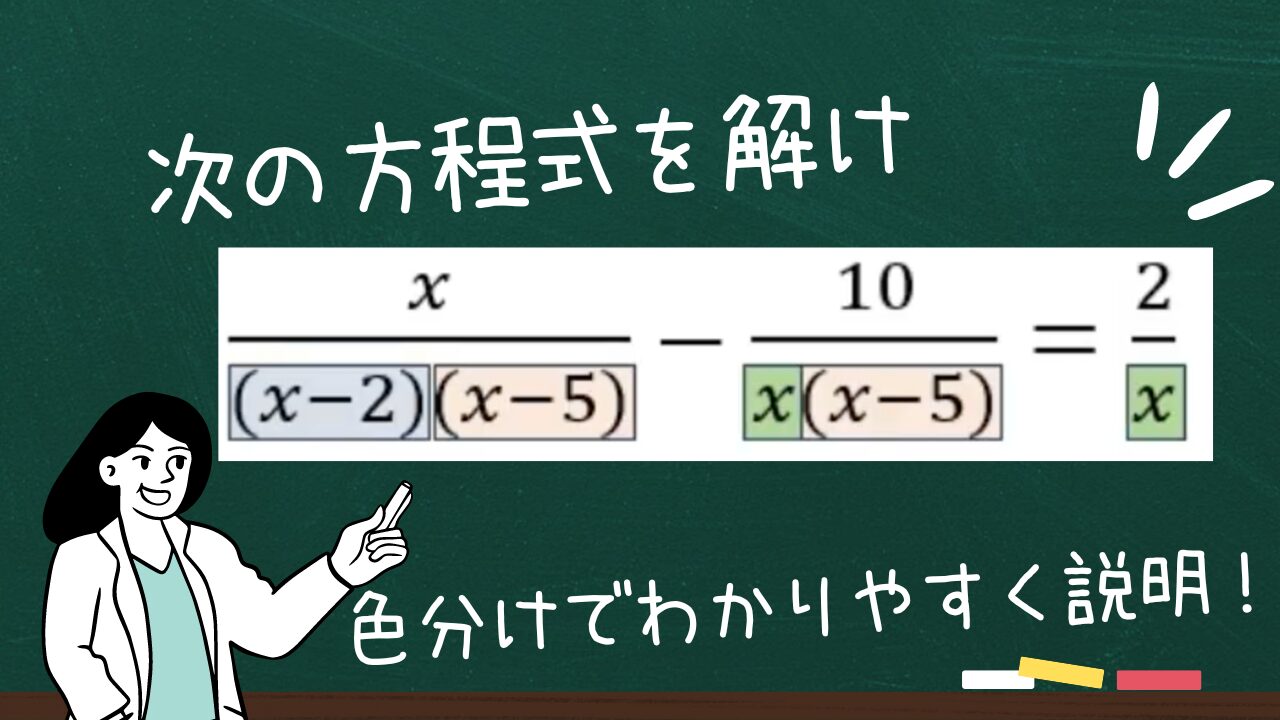
次の方程式を解け。
(1)$\displaystyle \frac{x}{x^2-7x+10} -\frac{10}{x^2-5x} =\frac{2}{x}$
(2)$\displaystyle \frac{x}{x^2+3x+2} =\frac{2}{x+2} -1$
この動画を見る
次の方程式を解け。
(1)$\displaystyle \frac{x}{x^2-7x+10} -\frac{10}{x^2-5x} =\frac{2}{x}$
(2)$\displaystyle \frac{x}{x^2+3x+2} =\frac{2}{x+2} -1$
大学入試問題#888「絶対にチャートに載ってる」 #奈良県立医科大学(2014)
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師：
ますただ
問題文全文(内容文)：
3次方程式
$x^3-6ax^2+9a^2x-4a=0$が相異なる3つの実数解をもつような$a$の範囲を求めよ。
出典：2014年奈良県立医科大学
この動画を見る
3次方程式
$x^3-6ax^2+9a^2x-4a=0$が相異なる3つの実数解をもつような$a$の範囲を求めよ。
出典：2014年奈良県立医科大学
二乗して➖2
福田のおもしろ数学196〜3重因子で割った余りを求める
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^n-1$ を $(x-1)^3$ で割った余りを求めよ。ただし、 $x \geqq 3$ とする。
この動画を見る
$x^n-1$ を $(x-1)^3$ で割った余りを求めよ。ただし、 $x \geqq 3$ とする。
福田のおもしろ数学194〜6次方程式をどう解くか
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$(x+7)^7=x^7+7^7$ を満たすすべての $x$ を求めよ。
この動画を見る
$(x+7)^7=x^7+7^7$ を満たすすべての $x$ を求めよ。
福田のおもしろ数学192〜連立方程式と対称式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師：
福田次郎
問題文全文(内容文)：
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + y^2 = 1 \\
x^3 + y^3 = 1
\end{array}
\right.
\end{eqnarray}$を解いて下さい。
この動画を見る
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + y^2 = 1 \\
x^3 + y^3 = 1
\end{array}
\right.
\end{eqnarray}$を解いて下さい。
福田の数学〜立教大学2024年理学部第4問〜3次方程式の実数解と整数解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$m, a, b, c, d, e, f, r, s, t$を自然数とする。このとき(1)~(5)に答えよ。ただし、(2)(3)の事実は(4)(5)で用いてよい。
(1)2次方程式$2x^2+5x+m=0$の解が有理数となるような自然数$m$をすべて求めよ。ただし、$p$が素数であるとき$\sqrt{p}$が無理数であることを用いてよい。
(2)3次方程式$x^3+ax^2+bx+c=0$の実数解は負の数であることを証明せよ。ただし、方程式$x^3+ax^2+bx+c=0$が少なくとも1つ実数解をもつことは証明せずに用いてよい。
(3)3次方程式$x^3+dx^2+ex+f=0$が整数$n$を解にもつとする。このとき$n$は$f$の約数であることを示せ。
(4)3次方程式$x^3+rx^2+rx+3=0$が整数解を少なくとも1つもつような自然数$r$をすべて求めよ。
(5)3次方程式$x^3+sx^2+tx+6=0$が異なる3つの整数を解にもつような自然数の組$(s, t)$をすべて求めよ。
この動画を見る
$m, a, b, c, d, e, f, r, s, t$を自然数とする。このとき(1)~(5)に答えよ。ただし、(2)(3)の事実は(4)(5)で用いてよい。
(1)2次方程式$2x^2+5x+m=0$の解が有理数となるような自然数$m$をすべて求めよ。ただし、$p$が素数であるとき$\sqrt{p}$が無理数であることを用いてよい。
(2)3次方程式$x^3+ax^2+bx+c=0$の実数解は負の数であることを証明せよ。ただし、方程式$x^3+ax^2+bx+c=0$が少なくとも1つ実数解をもつことは証明せずに用いてよい。
(3)3次方程式$x^3+dx^2+ex+f=0$が整数$n$を解にもつとする。このとき$n$は$f$の約数であることを示せ。
(4)3次方程式$x^3+rx^2+rx+3=0$が整数解を少なくとも1つもつような自然数$r$をすべて求めよ。
(5)3次方程式$x^3+sx^2+tx+6=0$が異なる3つの整数を解にもつような自然数の組$(s, t)$をすべて求めよ。
福田の数学〜立教大学2024年理学部第1問(4)〜係数が虚数の2次方程式の解
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$$iを虚数単位とする。複素数zはz^{ 2 }=3-2\sqrt{10 }iを満たし、かつzの実部は正であるとする。$$$$このとき、zの実部は\boxed{ カ }であり、虚部は\boxed{ キ }である。$$
この動画を見る
$$iを虚数単位とする。複素数zはz^{ 2 }=3-2\sqrt{10 }iを満たし、かつzの実部は正であるとする。$$$$このとき、zの実部は\boxed{ カ }であり、虚部は\boxed{ キ }である。$$
これなんで？ フルは↑
単元：
#数Ⅰ#数A#数Ⅱ#数と式#複素数と方程式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
これなんで？ フルは↑
【問題文】20×20
この動画を見る
これなんで？ フルは↑
【問題文】20×20
「20+20=200」になる理由を解説
単元：
#数Ⅰ#数A#数Ⅱ#数と式#複素数と方程式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
「20+20=200」になる理由を解説しています。
この動画を見る
「20+20=200」になる理由を解説しています。
これできる？
福田の数学〜慶應義塾大学2024年経済学部第1問(1)〜2次方程式が整数解をもつ条件
単元：
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$－($p$－9)$x$－$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
この動画を見る
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$－($p$－9)$x$－$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
この2つの違いは？
福田のおもしろ数学165〜4次方程式を工夫して解こう
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$(x+2)^4$+$(x+1)^4$=17 を解け。
この動画を見る
$(x+2)^4$+$(x+1)^4$=17 を解け。
福田の数学〜九州大学2024年理系第2問〜複素数平面と高次方程式の解
単元：
#数Ⅱ#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 整式$f(z)$=$z^6$+$z^4$+$z^2$+1
について、以下の問いに答えよ。
(1)$f(z)$=0 を満たす全ての複素数$z$に対して、|$z$|=1 が成り立つことを示せ。
(2)次の条件を満たす複素数$w$を全て求めよ。
条件：$f(z)$=0 を満たす全ての複素数$z$に対して
$f(wz)$=0 が成り立つ。
この動画を見る
$\Large\boxed{2}$ 整式$f(z)$=$z^6$+$z^4$+$z^2$+1
について、以下の問いに答えよ。
(1)$f(z)$=0 を満たす全ての複素数$z$に対して、|$z$|=1 が成り立つことを示せ。
(2)次の条件を満たす複素数$w$を全て求めよ。
条件：$f(z)$=0 を満たす全ての複素数$z$に対して
$f(wz)$=0 が成り立つ。