 複素数と方程式
複素数と方程式
 複素数と方程式
複素数と方程式
できるように作られた因数分解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 36x^4+24x^3+67x^2+24x+36$
これを因数分解せよ.
この動画を見る
$ 36x^4+24x^3+67x^2+24x+36$
これを因数分解せよ.
東北大文系 虚数のナイスな問題

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#数列#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
この動画を見る
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
福田の入試問題解説〜慶應義塾大学2022年医学部第1問(2)〜高次式の因数分解

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)整式$x^5+x^4+x^3+x^2+x+1$は、整数を係数とし、次数が1以上で、
かつ最高次の項の係数が1であるような3つの整式$\boxed{\ \ イ\ \ },\boxed{\ \ ウ\ \ },\boxed{\ \ エ\ \ }$の積に
因数分解せよ。
2022慶應義塾大学医学部過去問
この動画を見る
(2)整式$x^5+x^4+x^3+x^2+x+1$は、整数を係数とし、次数が1以上で、
かつ最高次の項の係数が1であるような3つの整式$\boxed{\ \ イ\ \ },\boxed{\ \ ウ\ \ },\boxed{\ \ エ\ \ }$の積に
因数分解せよ。
2022慶應義塾大学医学部過去問
大学入試問題#228 愛知教育大学(2012) 3乗根の計算

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#愛知教育大学
指導講師:
ますただ
問題文全文(内容文):
$\alpha=\sqrt[ 3 ]{ 5\sqrt{ 2 }+7 }-\sqrt[ 3 ]{ 5\sqrt{ 2 }-7 }$
(1)$\alpha^3$を$\alpha$で表せ
(2)$\alpha$は整数であることを示せ
出典:2012年愛知教育大学 入試問題
この動画を見る
$\alpha=\sqrt[ 3 ]{ 5\sqrt{ 2 }+7 }-\sqrt[ 3 ]{ 5\sqrt{ 2 }-7 }$
(1)$\alpha^3$を$\alpha$で表せ
(2)$\alpha$は整数であることを示せ
出典:2012年愛知教育大学 入試問題
ただの連立方程式
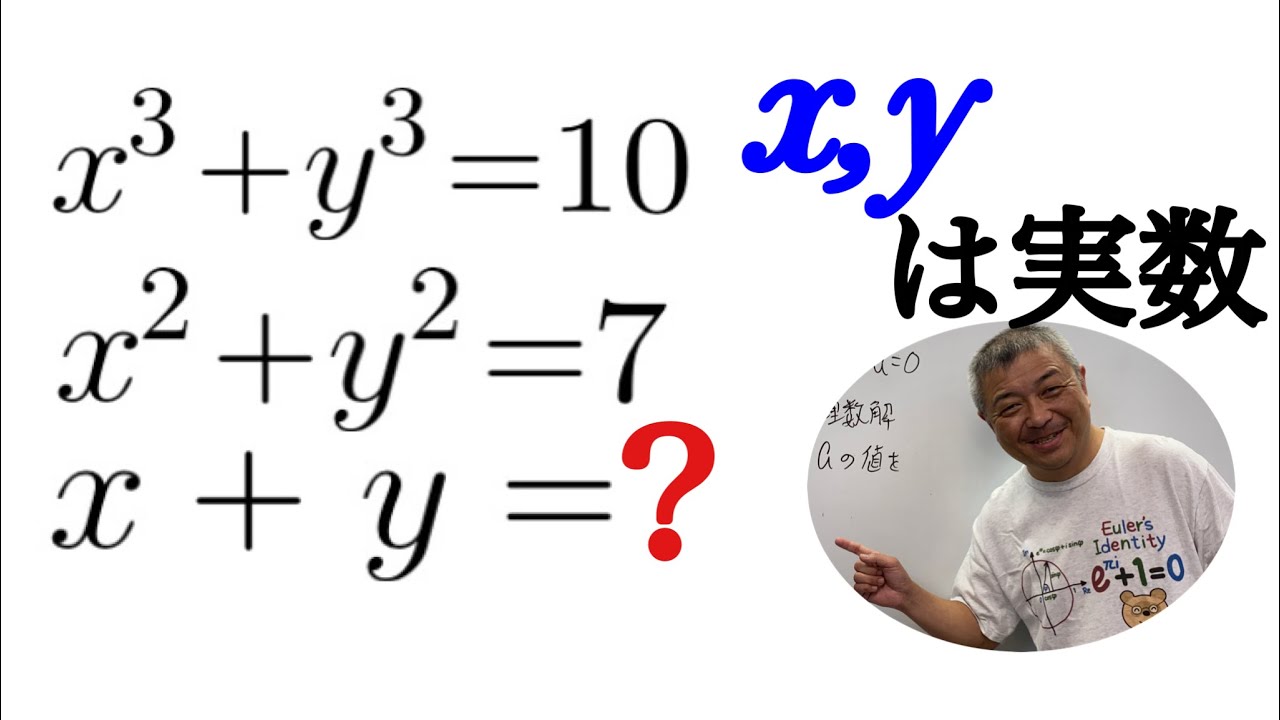
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは実数とする.
x^3+y^3=10,x^2+y^2=7,x+y=?$
これを解け.
この動画を見る
x,yは実数とする.
x^3+y^3=10,x^2+y^2=7,x+y=?$
これを解け.
綺麗な連立4元方程式
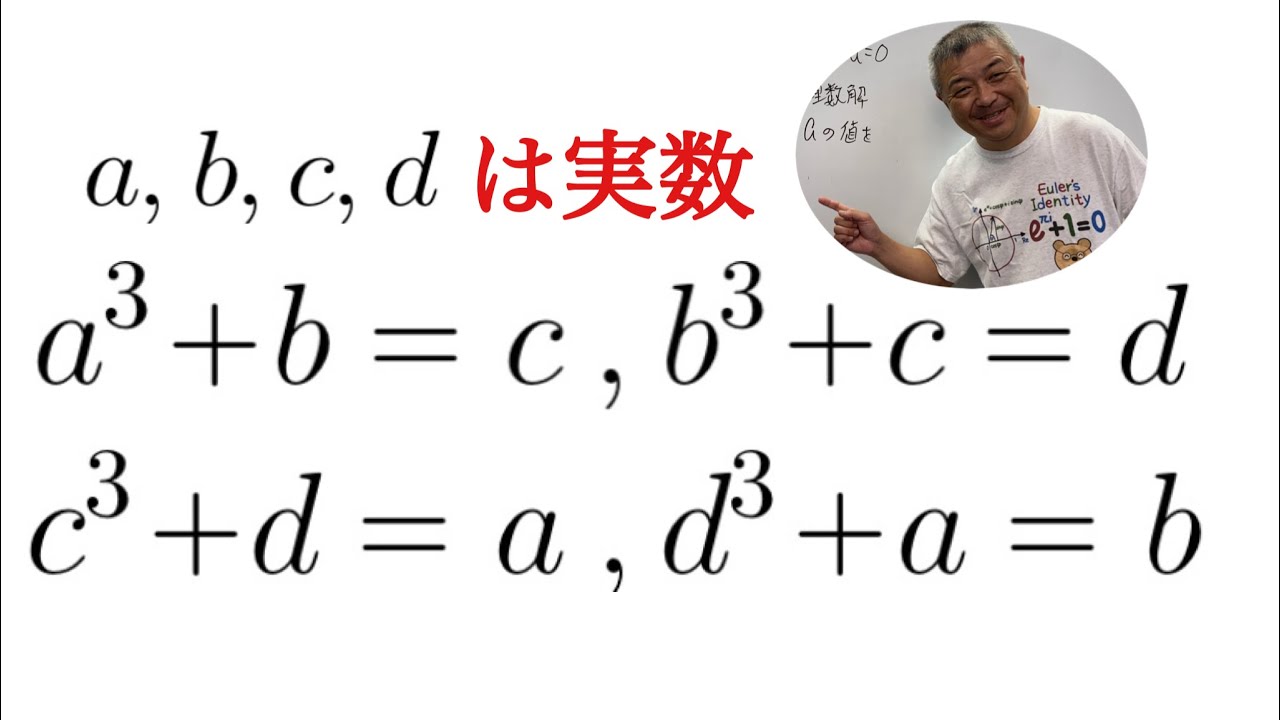
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c,d$を実数とする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^3+b=c \\
b^3+c=d \\
c^3+d=a \\
d^3+a=b \\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$a,b,c,d$を実数とする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^3+b=c \\
b^3+c=d \\
c^3+d=a \\
d^3+a=b \\
\end{array}
\right.
\end{eqnarray}$
こう見えて数3範囲
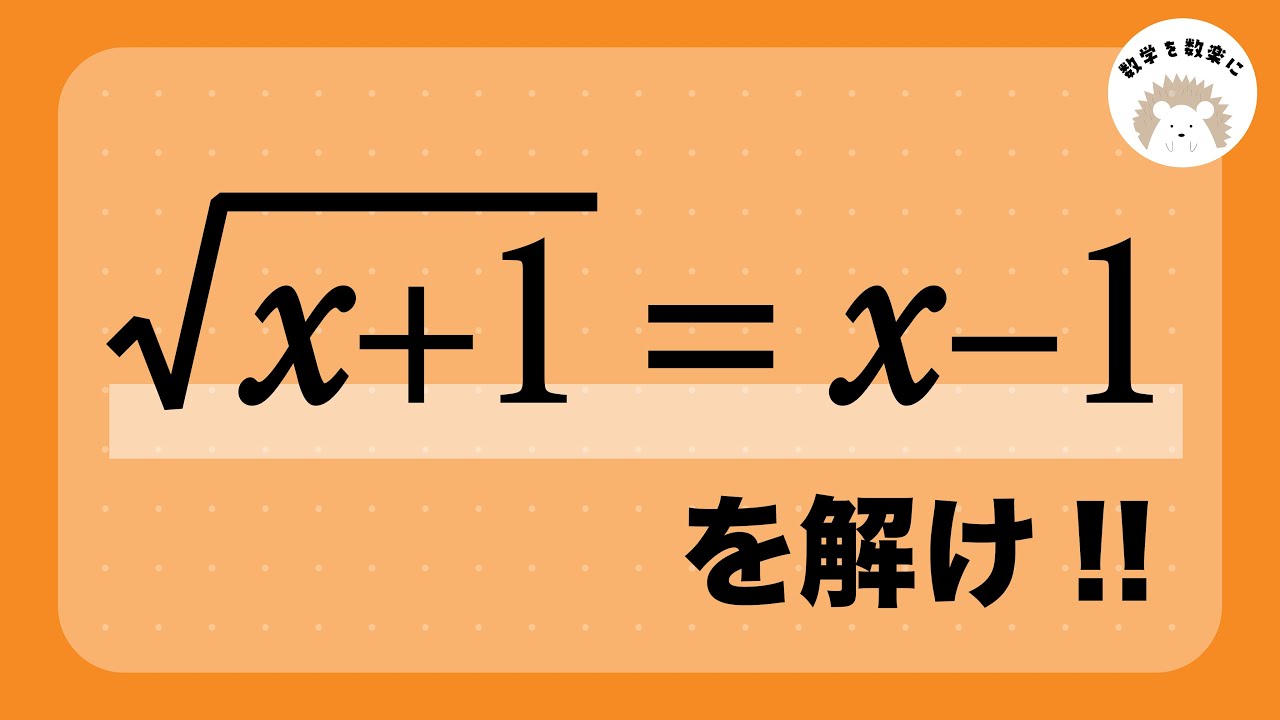
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{x+1} = x-1$を解け
この動画を見る
$\sqrt{x+1} = x-1$を解け
連立方程式
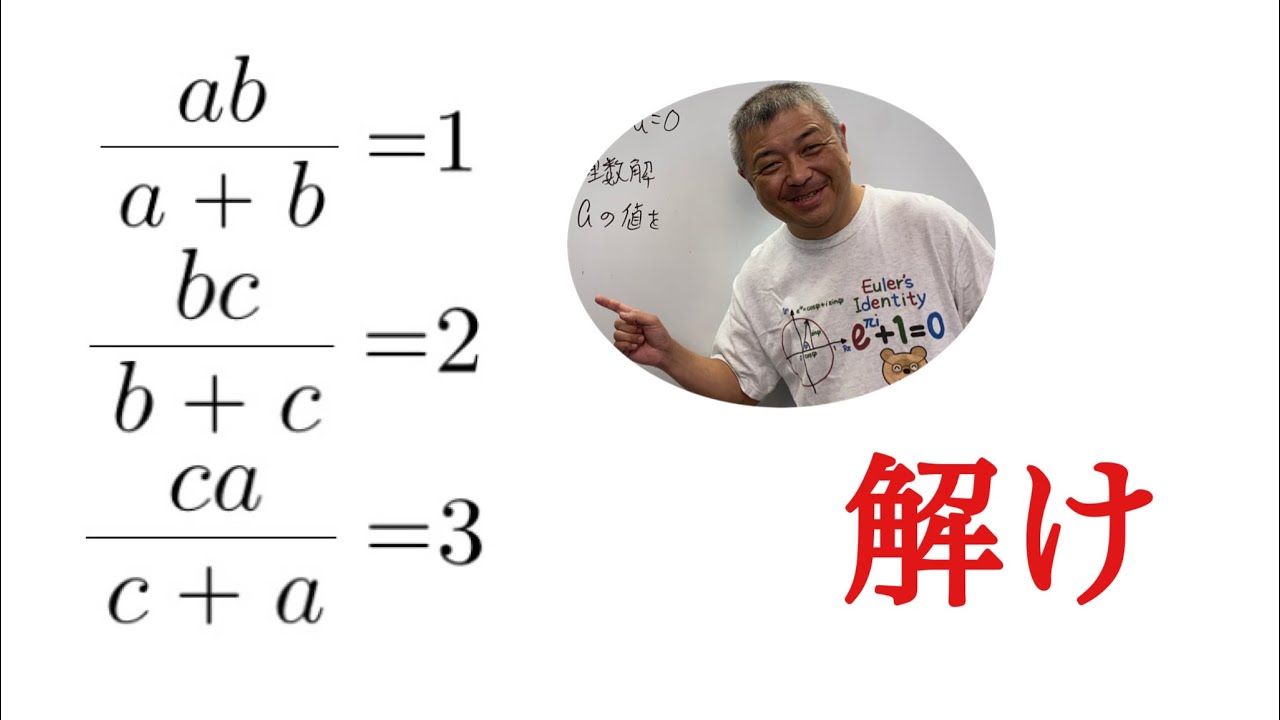
単元:
#連立方程式#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{ab}{a+b}=1 \\
\dfrac{bc}{b+c}=2 \\
\dfrac{ca}{c+a}=3 \\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{ab}{a+b}=1 \\
\dfrac{bc}{b+c}=2 \\
\dfrac{ca}{c+a}=3 \\
\end{array}
\right.
\end{eqnarray}$
式の値 基本
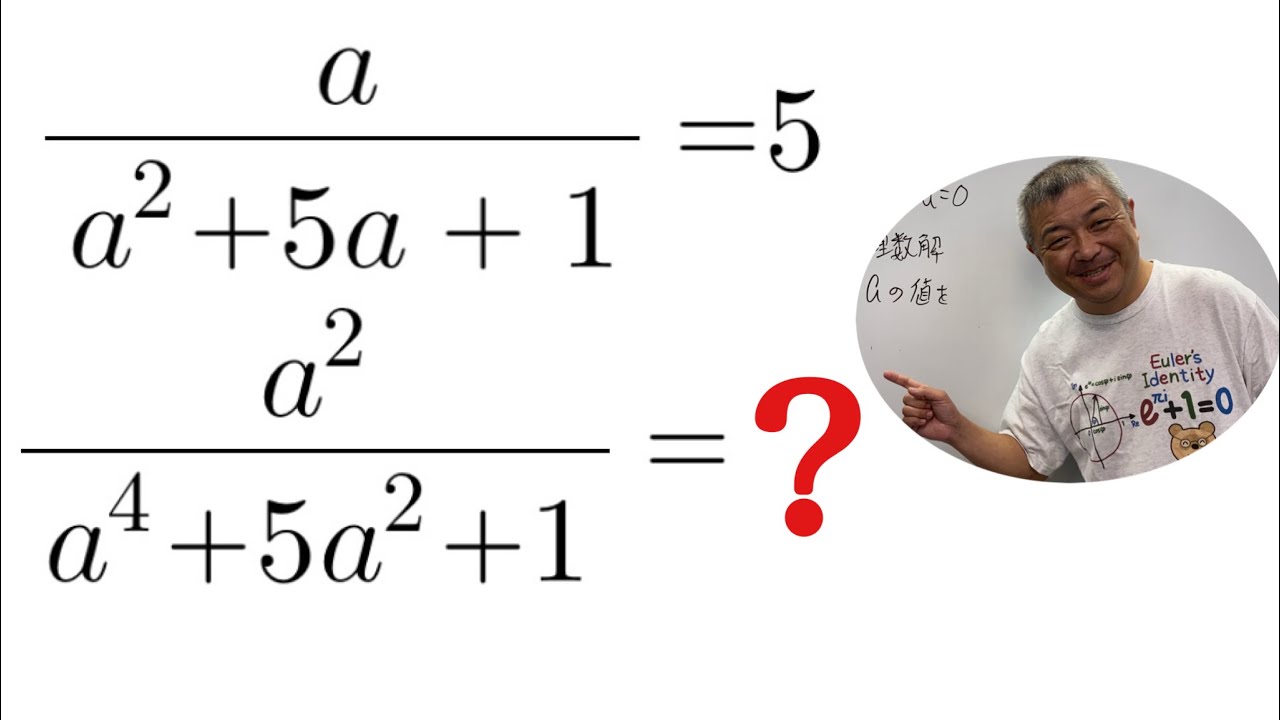
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{a}{a^2+5a+1}=5$のとき,
$\dfrac{a^2}{a^4+5a^2+1}=?$
これを解け.
この動画を見る
$ \dfrac{a}{a^2+5a+1}=5$のとき,
$\dfrac{a^2}{a^4+5a^2+1}=?$
これを解け.
指数方程式 (数II)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$16^x-9 \times 4^x +8 = 0$を解け
この動画を見る
$16^x-9 \times 4^x +8 = 0$を解け
4次方程式の解でできた式の値
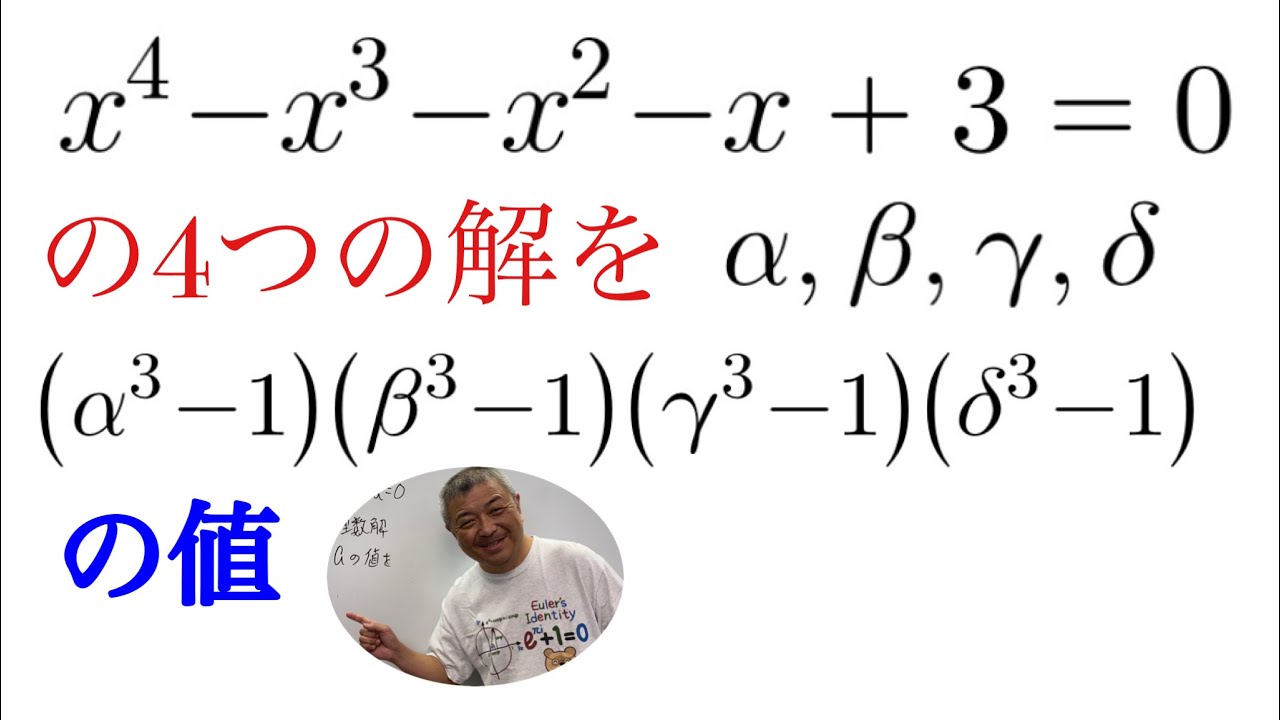
単元:
#数Ⅱ#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^4-x^3-x^2-x+3=0$の4つの解を$\alpha,\beta,\delta,\zeta$とする.
$(\alpha^3-1)(\beta^3-1)(\delta^3-1)(\zeta^3-1)$の値を求めよ.
この動画を見る
$ x^4-x^3-x^2-x+3=0$の4つの解を$\alpha,\beta,\delta,\zeta$とする.
$(\alpha^3-1)(\beta^3-1)(\delta^3-1)(\zeta^3-1)$の値を求めよ.
藤田医科大学 式の最小値
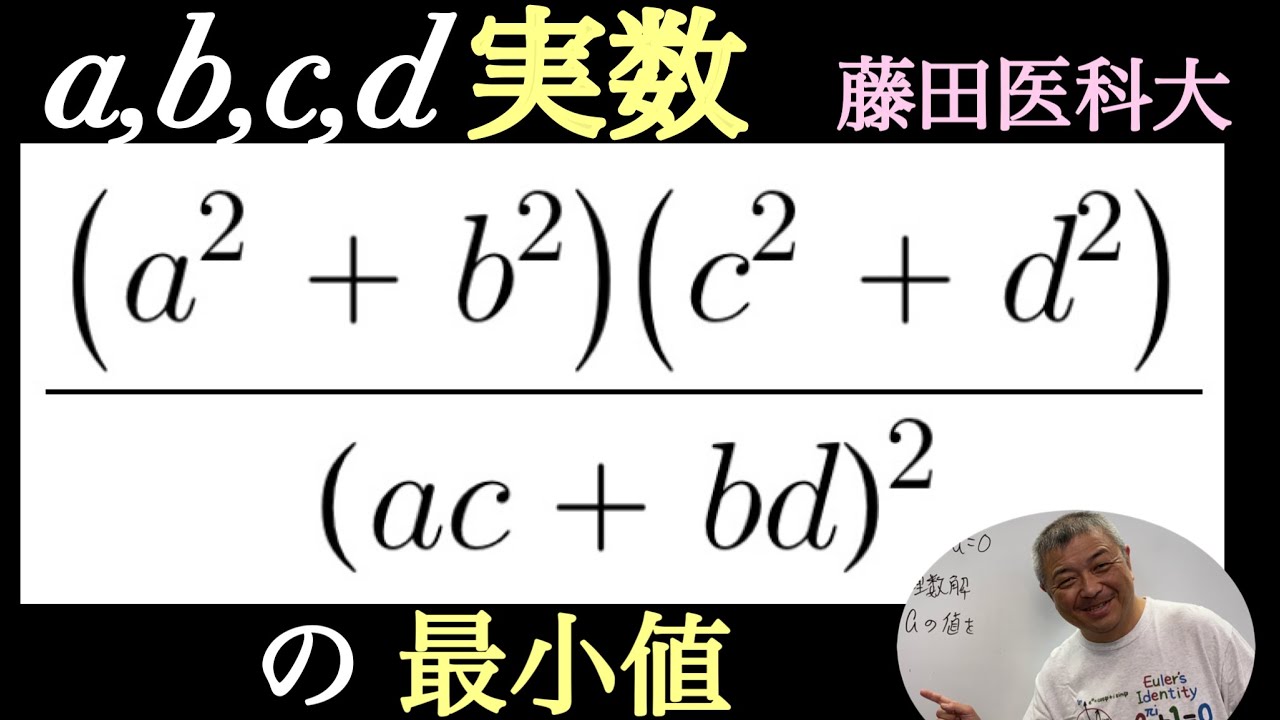
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#藤田医科大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a,b,c,dは実数である.
$\dfrac{(a^2+b^2)(c^2+d^2)}{(ac+bd)^2}$の最小値を求めよ.
この動画を見る
$ a,b,c,dは実数である.
$\dfrac{(a^2+b^2)(c^2+d^2)}{(ac+bd)^2}$の最小値を求めよ.
中学生も解けるルートを含む方程式
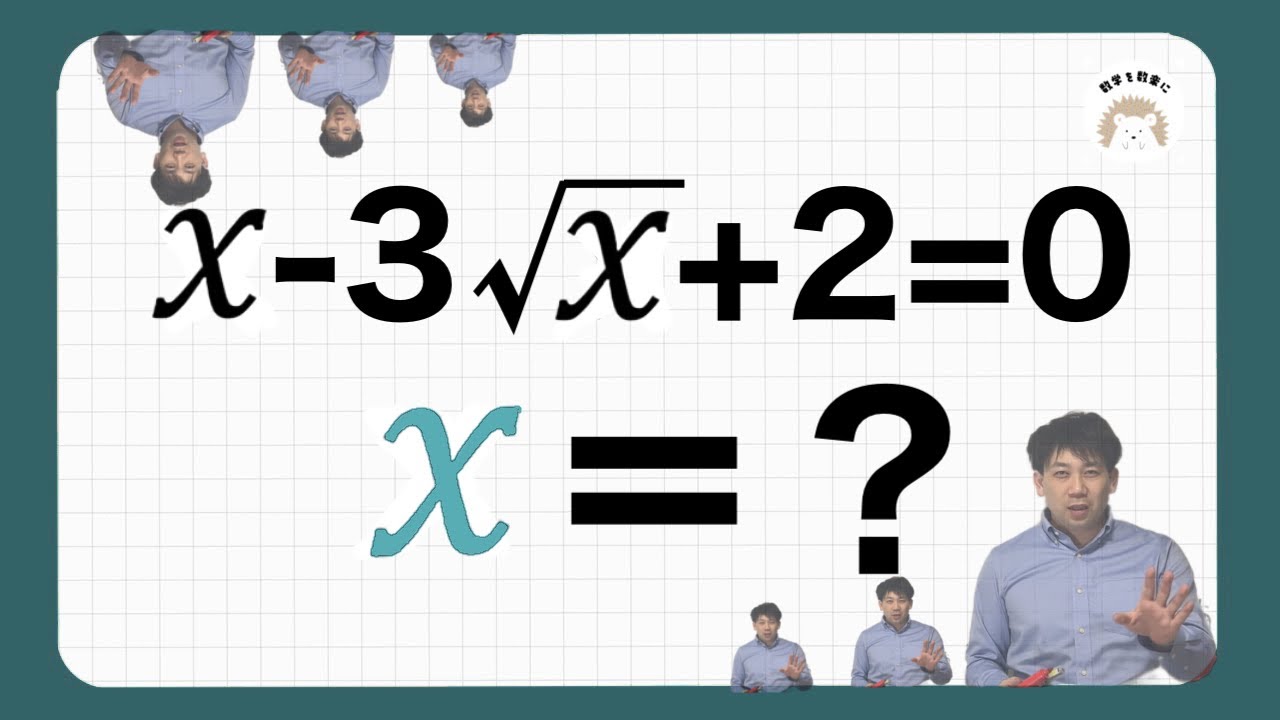
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x-3 \sqrt x +2 = 0
x=?
この動画を見る
x-3 \sqrt x +2 = 0
x=?
方程式を解け!

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
次の方程式を解け。
(1) $\frac{x}{2022} = 0$
(2) $\frac{2022}{x} = 0$
この動画を見る
次の方程式を解け。
(1) $\frac{x}{2022} = 0$
(2) $\frac{2022}{x} = 0$
解けるように作られた指数方程式

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)^{x-y}=2 \\
2^{y-x},(x+y)=1
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)^{x-y}=2 \\
2^{y-x},(x+y)=1
\end{array}
\right.
\end{eqnarray}$
これを解け.
立命館(文系)複素数の計算

単元:
#数Ⅱ#複素数と方程式#複素数#大学入試過去問(英語)#立命館大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^6=1$の4つの虚数解のうちの1つを$\alpha$とする.
$(1-\alpha)(1-\alpha^3)(1-\alpha^5)$の値は$\Box$か$\Box$か.
立命館大(文系)過去問
この動画を見る
$x^6=1$の4つの虚数解のうちの1つを$\alpha$とする.
$(1-\alpha)(1-\alpha^3)(1-\alpha^5)$の値は$\Box$か$\Box$か.
立命館大(文系)過去問
早稲田(教育)見た目は数2か数3 中身は中学入試
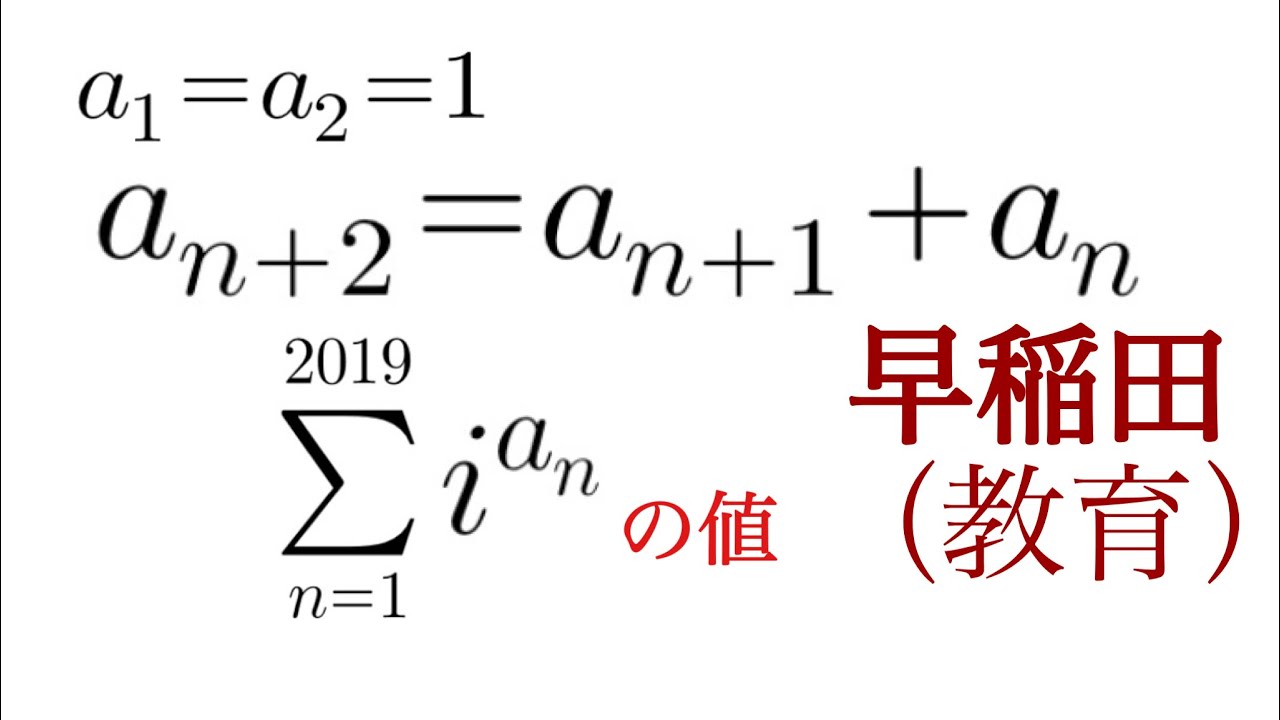
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#数列#早稲田大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=a_2=1,a_{n+2}=a_{n+1}+a_n,\displaystyle \sum_{n=1}^{2019} ia_n,$
$i$は虚数単位である.これを解け.
早稲田大(教育)過去問
この動画を見る
$ a_1=a_2=1,a_{n+2}=a_{n+1}+a_n,\displaystyle \sum_{n=1}^{2019} ia_n,$
$i$は虚数単位である.これを解け.
早稲田大(教育)過去問
2次方程式の因数分解や解の公式が不要な新しい解き方の証明

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2次方程式の因数分解や解の公式が不要な新しい解き方の証明
この動画を見る
2次方程式の因数分解や解の公式が不要な新しい解き方の証明
福田の数学〜九州大学2022年文系第3問〜高次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$k$を実数とし、整式f(x)を
$f(x)=x^4+6x^3-kx^2+2kx-64$
で定める。方程式$f(x)=0$が虚数解をもつとき、以下の問いに答えよ。
(1)f(x)は$x-2$で割り切れることを示せ。
(2)方程式$f(x)=0$は負の実数解をもつことを示せ。
(3)方程式$f(x)=0$の全ての実数解が整数であり、
すべての虚数解の実部と虚部が共に整数であるとする。
このような$k$を全て求めよ。
2022九州大学文系過去問
この動画を見る
$k$を実数とし、整式f(x)を
$f(x)=x^4+6x^3-kx^2+2kx-64$
で定める。方程式$f(x)=0$が虚数解をもつとき、以下の問いに答えよ。
(1)f(x)は$x-2$で割り切れることを示せ。
(2)方程式$f(x)=0$は負の実数解をもつことを示せ。
(3)方程式$f(x)=0$の全ての実数解が整数であり、
すべての虚数解の実部と虚部が共に整数であるとする。
このような$k$を全て求めよ。
2022九州大学文系過去問
福田の数学〜九州大学2022年文系第1問〜絶対値の付いた放物線と直線で囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#2次関数#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
この動画を見る
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
問題の背景を探る ハンガリーJr数学Olympic
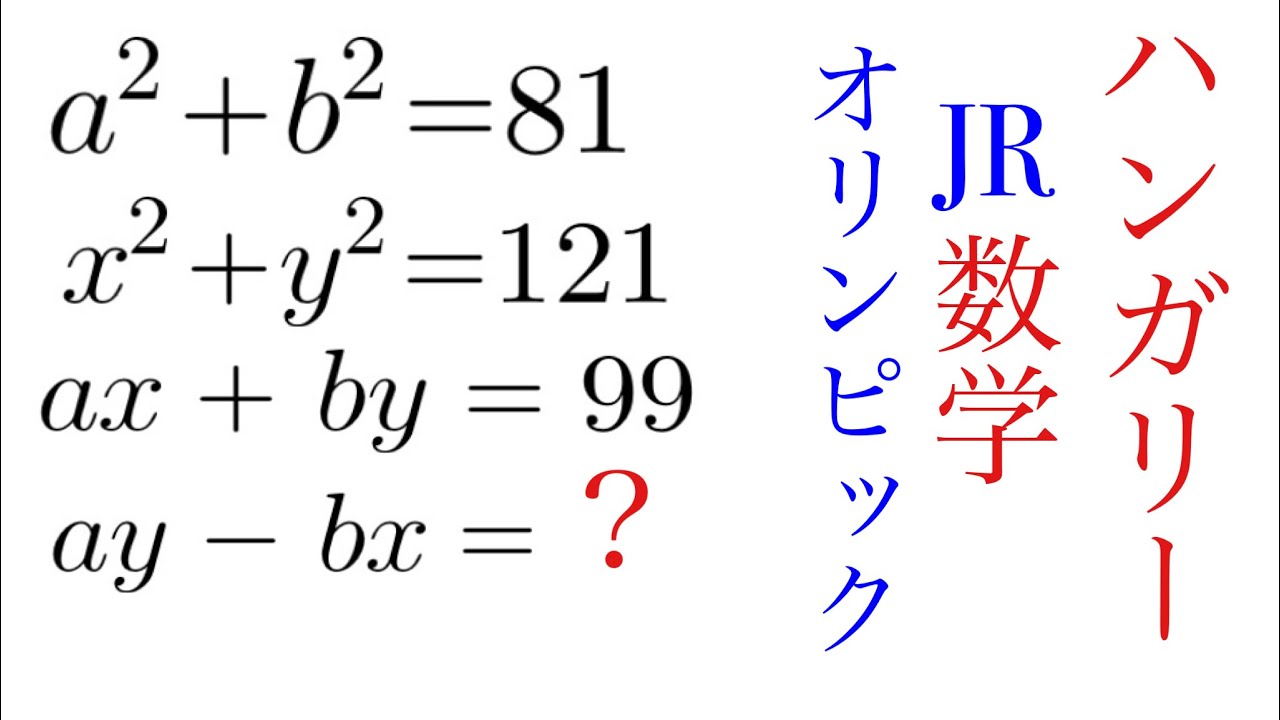
単元:
#複素数平面#円#三角関数#複素数#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a^2+b^2=81$
$x^2+y^2=121$
$ax+by=99$
$ay-bx=?$
これを解け.
ハンガリーjr数学オリンピック過去問
この動画を見る
$ a^2+b^2=81$
$x^2+y^2=121$
$ax+by=99$
$ay-bx=?$
これを解け.
ハンガリーjr数学オリンピック過去問
整式の割り算!頻出です【山梨大学 入試問題】【数学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$x^{2014}$を整式$x^4+x^3+x^2+x+1$で割った余りを求めよ。
山梨大過去問
この動画を見る
整式$x^{2014}$を整式$x^4+x^3+x^2+x+1$で割った余りを求めよ。
山梨大過去問
東京電機大 複素数のべき乗

単元:
#複素数と方程式#複素数#指数関数#数列
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(1+2i)^n=x_n+y_ni$
(1)$x^2_n+y^2_n$を求めよ.
(2)$x_{n+2}$を$x_{n+1}$と$x_n$で表せ.
(3)$x_n$と$y_n$の最大公約数を求めよ.
東京電機大過去問
この動画を見る
$(1+2i)^n=x_n+y_ni$
(1)$x^2_n+y^2_n$を求めよ.
(2)$x_{n+2}$を$x_{n+1}$と$x_n$で表せ.
(3)$x_n$と$y_n$の最大公約数を求めよ.
東京電機大過去問
中学生も解ける4次方程式

【因数定理】コツがあるんです【数学 解説動画】

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の式を因数分解せよ。
(1)$x^3+4x^2-6x-27$
(2)$x^3+6x^2-6x+7$
この動画を見る
次の式を因数分解せよ。
(1)$x^3+4x^2-6x-27$
(2)$x^3+6x^2-6x+7$
きっと良問

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
P(x)はxの3次式でP(11)=11,P(12)=12,P(13)=14,P(14)=15である.
P(15)のときはいくつであるか求めよ.
この動画を見る
P(x)はxの3次式でP(11)=11,P(12)=12,P(13)=14,P(14)=15である.
P(15)のときはいくつであるか求めよ.
中国Jr 数学Olympic あっと驚く解法も

単元:
#数学検定・数学甲子園・数学オリンピック等#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^5=1,x \neq 1$とするとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x^8}$の値を求めよ.
中国jr数学オリンピック過去問
この動画を見る
$ x^5=1,x \neq 1$とするとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x^8}$の値を求めよ.
中国jr数学オリンピック過去問
簡単な問題

単元:
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \omega=1(\omega \neq 1)$であり,
$x=a+b $
$y=a\omega+b\omega^2 $
$z=a\omega^2+b\omega $である.
$ x^3+y^3+z^3$の値をa,bで表せ.
この動画を見る
$ \omega=1(\omega \neq 1)$であり,
$x=a+b $
$y=a\omega+b\omega^2 $
$z=a\omega^2+b\omega $である.
$ x^3+y^3+z^3$の値をa,bで表せ.
2分で解ける問題

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+\dfrac{1}{x^2}=\sqrt2 $のとき,$ x^{2022}+\dfrac{1}{x^{2022}}$の値を求めよ.
この動画を見る
$ x^2+\dfrac{1}{x^2}=\sqrt2 $のとき,$ x^{2022}+\dfrac{1}{x^{2022}}$の値を求めよ.
方程式を解く。
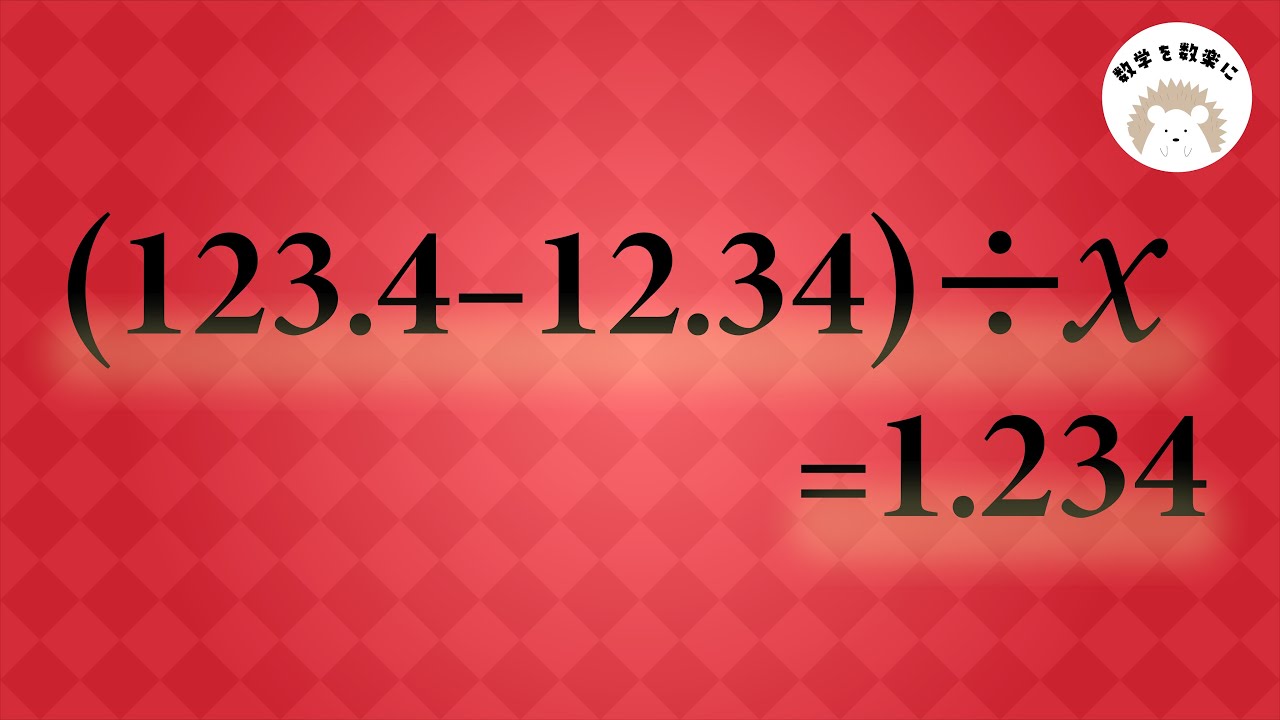
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(123.4-12.34) \div x =1.234$
この動画を見る
$(123.4-12.34) \div x =1.234$
