 図形と方程式
図形と方程式
 図形と方程式
図形と方程式
福田の入試問題解説〜北海道大学2012年理系数学第4問〜2次関数と2次不等式、領域
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$ 実数$a,b$に対して、$f(x)=x^2-2ax+b,g(x)$$=x^2-2bx+a$ とおく。
(1)$a \ne b$のとき、$f(c)=g(c)$を満たす実数cを求めよ。
(2)(1)で求めた$c$について、$a,b$が条件$a \lt c \lt b$を満たすとする。このとき
連立不等式
$f(x) \lt 0$ かつ $g(x) \lt 0$
が解をもつための必要十分条件を$a,b$を用いて表せ。
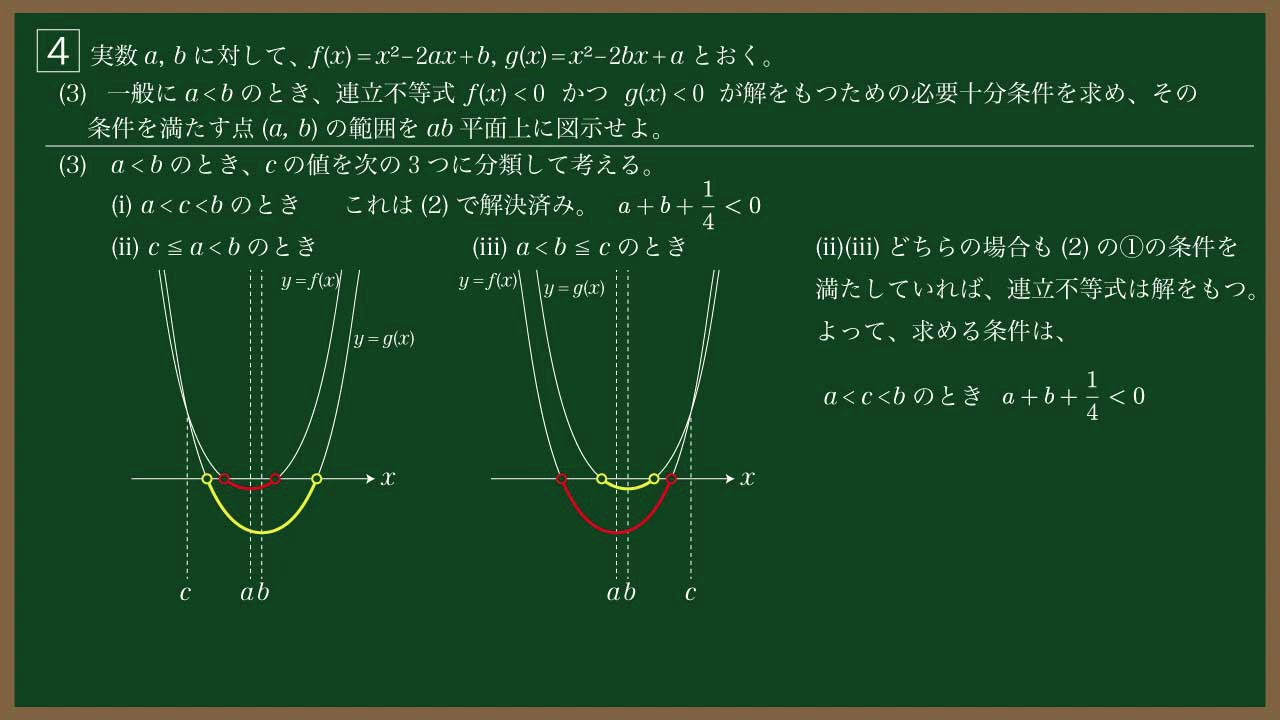
(3)一般に$a \lt b$のとき、連立不等式
$f(x) \lt 0$ かつ $g(x) \lt 0$
が解をもつための必要十分条件を求め、その条件を満たす
点$(a,b)$の範囲を$ab$平面上に図示せよ。
この動画を見る
${\Large\boxed{4}}$ 実数$a,b$に対して、$f(x)=x^2-2ax+b,g(x)$$=x^2-2bx+a$ とおく。
(1)$a \ne b$のとき、$f(c)=g(c)$を満たす実数cを求めよ。
(2)(1)で求めた$c$について、$a,b$が条件$a \lt c \lt b$を満たすとする。このとき
連立不等式
$f(x) \lt 0$ かつ $g(x) \lt 0$
が解をもつための必要十分条件を$a,b$を用いて表せ。
(3)一般に$a \lt b$のとき、連立不等式
$f(x) \lt 0$ かつ $g(x) \lt 0$
が解をもつための必要十分条件を求め、その条件を満たす
点$(a,b)$の範囲を$ab$平面上に図示せよ。
福田の一夜漬け数学〜図形と方程式〜領域(11)証明問題への領域の利用、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $|a+b| \leqq 1$ かつ $|a-b| \leqq 1 \iff |a|+|b| \leqq 1$ を証明せよ。
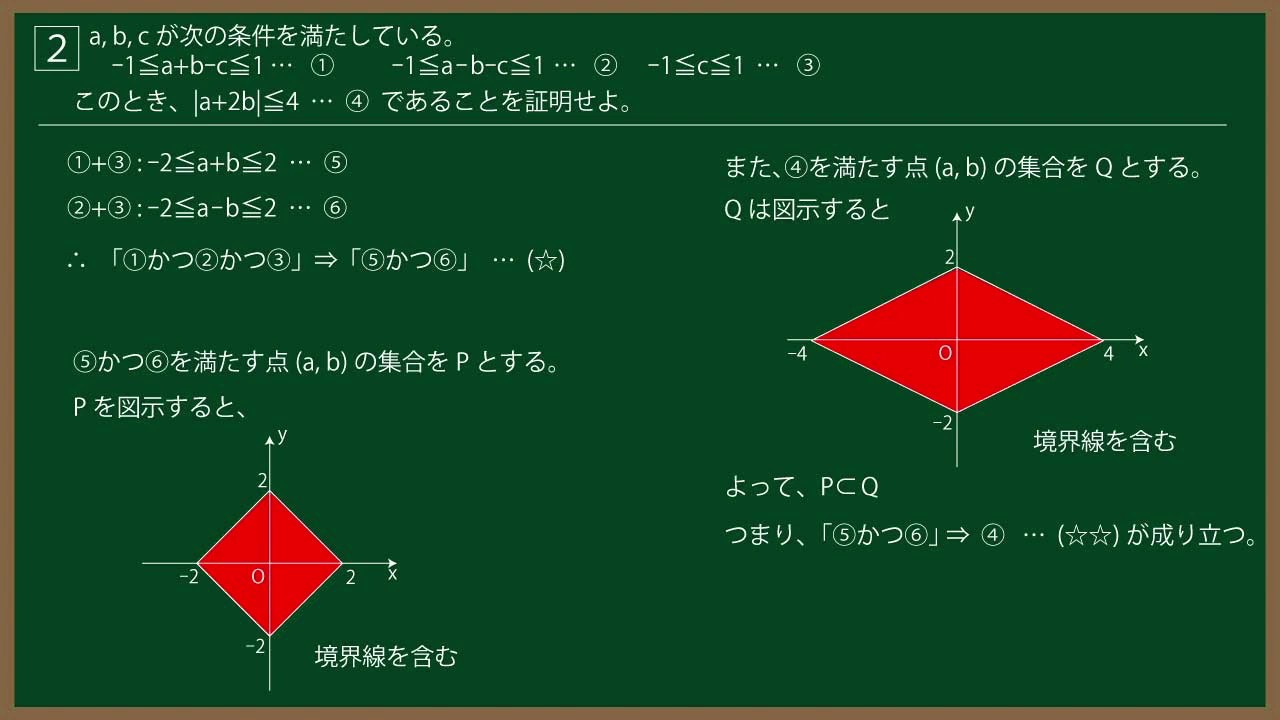
${\Large\boxed{2}}$ $a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
-1 \leqq a+b-c \leqq 1 \cdots①\\
-1 \leqq a-b-c \leqq 1 \cdots②\\
-1 \leqq c \leqq 1 \cdots③\\
\end{array}
\right.
\end{eqnarray}$
このとき、$|a++2b| \leqq 4$ $\cdots$④ であることを証明せよ。
この動画を見る
${\Large\boxed{1}}$ $|a+b| \leqq 1$ かつ $|a-b| \leqq 1 \iff |a|+|b| \leqq 1$ を証明せよ。
${\Large\boxed{2}}$ $a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
-1 \leqq a+b-c \leqq 1 \cdots①\\
-1 \leqq a-b-c \leqq 1 \cdots②\\
-1 \leqq c \leqq 1 \cdots③\\
\end{array}
\right.
\end{eqnarray}$
このとき、$|a++2b| \leqq 4$ $\cdots$④ であることを証明せよ。
福田の一夜漬け数学〜図形と方程式〜領域(10)対称式の問題(その2)京都大学の問題に挑戦、高校2年生

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 実数$x,y$が条件$x^2+xy+y^2=6$ を満たしながら動くとき、
$x^2y+xy^2-x^2-2xy-y^2$$+x+y$
が取り得る値の範囲を求めよ。
この動画を見る
${\Large\boxed{1}}$ 実数$x,y$が条件$x^2+xy+y^2=6$ を満たしながら動くとき、
$x^2y+xy^2-x^2-2xy-y^2$$+x+y$
が取り得る値の範囲を求めよ。
福田の一夜漬け数学〜数学II 図形と方程式〜軌跡(9) 対称式の問題(その1)、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 実数$x,y$が$x^2+y^2 \leqq 8$ を満たしながら変化するとき
(1)点$P(x+y,xy)$の存在範囲を図示せよ。
(2)$x+y+xy$の最大値、最小値を求めよ。
この動画を見る
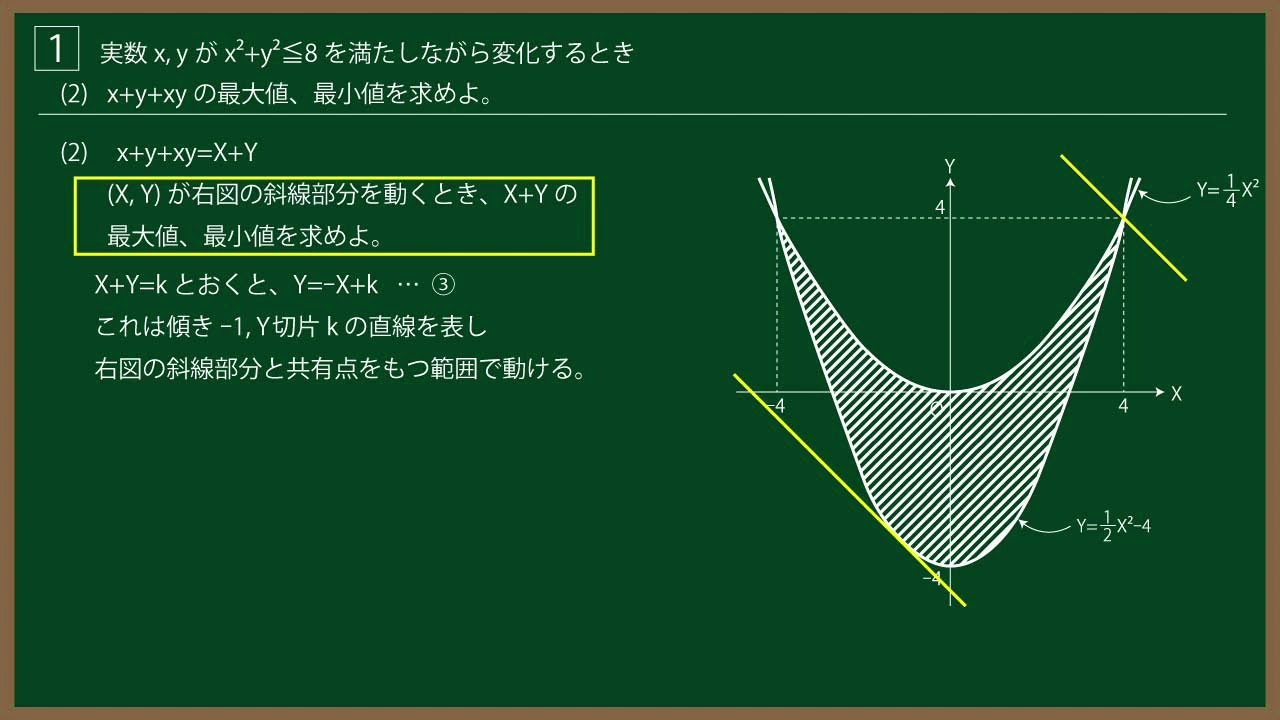
${\Large\boxed{1}}$ 実数$x,y$が$x^2+y^2 \leqq 8$ を満たしながら変化するとき
(1)点$P(x+y,xy)$の存在範囲を図示せよ。
(2)$x+y+xy$の最大値、最小値を求めよ。
福田の一夜漬け数学〜図形と方程式〜領域(8)直線の通過領域(実践編2)、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
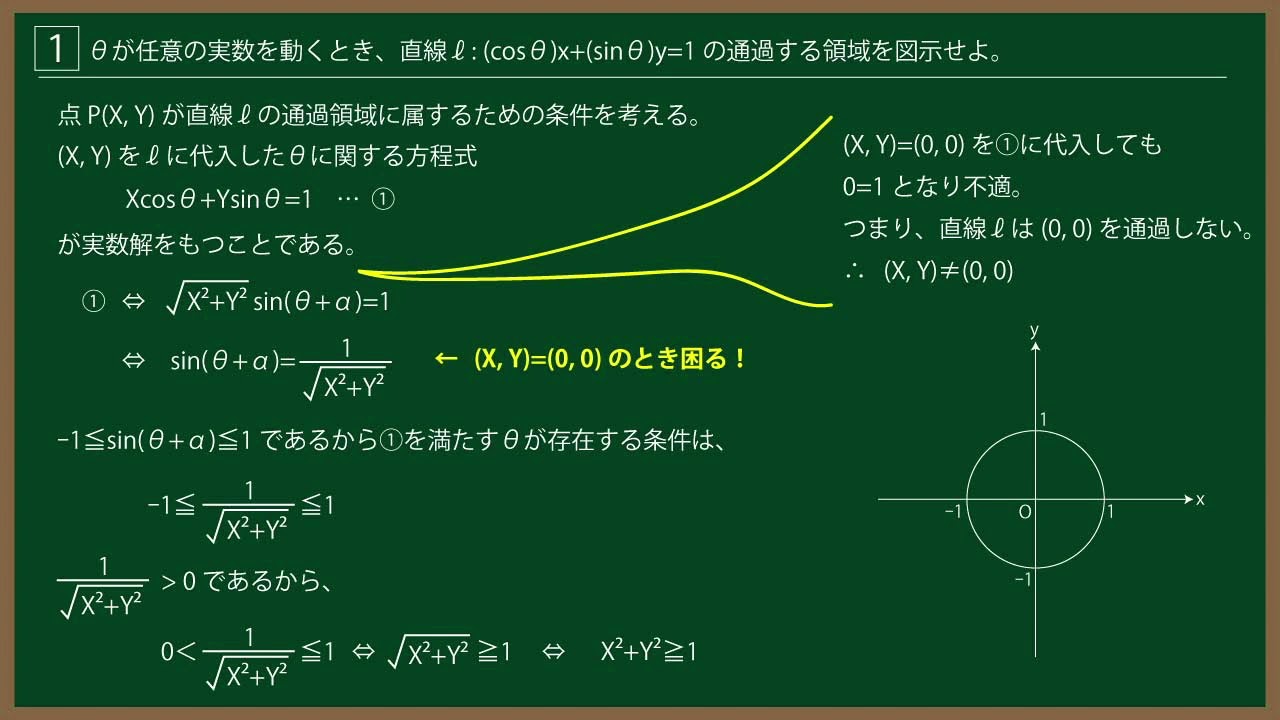
${\Large\boxed{1}}$ $\theta$が任意の実数を動くとき、直線$\ell:(\cos\theta)\ x+(\sin\theta)\ y=1$
の通過する領域を図示せよ。
この動画を見る
${\Large\boxed{1}}$ $\theta$が任意の実数を動くとき、直線$\ell:(\cos\theta)\ x+(\sin\theta)\ y=1$
の通過する領域を図示せよ。
福田の一夜漬け数学〜図形と方程式〜領域(7)直線の通過領域(実践編)、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
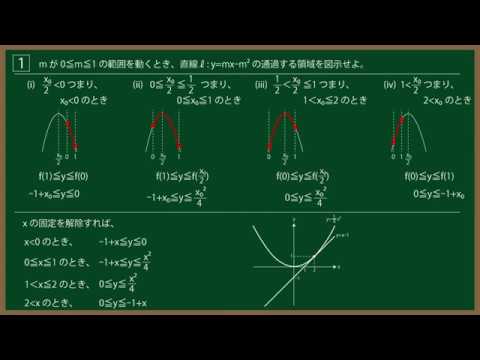
${\Large\boxed{1}}$ $m$が$0 \leqq m \leqq 1$の範囲を動くとき、直線$\ell:y=mx-m^2$
の通過する領域を図示せよ。
この動画を見る
${\Large\boxed{1}}$ $m$が$0 \leqq m \leqq 1$の範囲を動くとき、直線$\ell:y=mx-m^2$
の通過する領域を図示せよ。
福田の一夜漬け数学〜図形と方程式〜領域(6)直線の通過領域(基本)、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
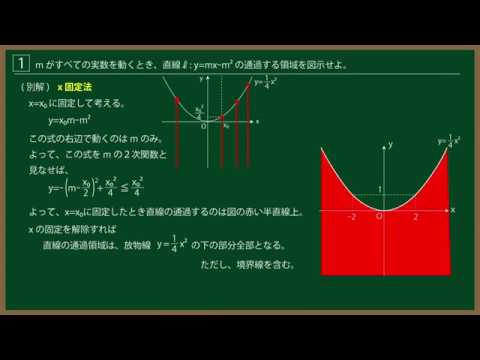
${\Large\boxed{1}}$ $m$が全ての実数を動くとき、直線$\ell:y=mx-m^2$
の通過する領域を図示せよ。
この動画を見る
${\Large\boxed{1}}$ $m$が全ての実数を動くとき、直線$\ell:y=mx-m^2$
の通過する領域を図示せよ。
福田の一夜漬け数学〜図形と方程式〜領域(5)正領域・負領域、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 2点$O(0,0),A(1,2)$に対し、次の問いに答えよ。
(1)線分$OA$と直線$y=ax+b$ が共有点をもつような$(a,b)$を
$ab$平面上に図示せよ。
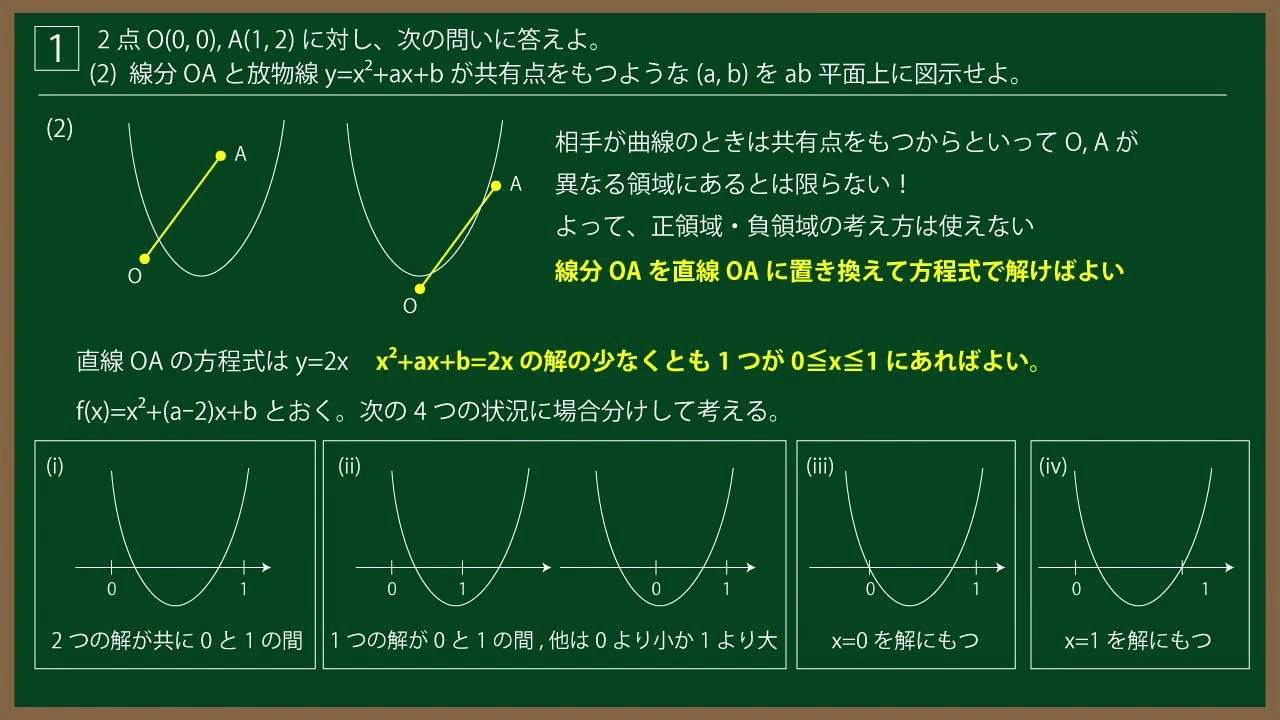
(2)線分$OA$と放物線$y=x^2+ax+b$ が共有点をもつような$(a,b)$を
$ab$平面上に図示せよ。
この動画を見る
${\Large\boxed{1}}$ 2点$O(0,0),A(1,2)$に対し、次の問いに答えよ。
(1)線分$OA$と直線$y=ax+b$ が共有点をもつような$(a,b)$を
$ab$平面上に図示せよ。
(2)線分$OA$と放物線$y=x^2+ax+b$ が共有点をもつような$(a,b)$を
$ab$平面上に図示せよ。
福田の一夜漬け数学〜図形と方程式〜領域(4)領域における最大最小、高校2年生

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 不等式$-1 \leqq y-x \leqq 1,$ $-1 \leqq x+y \leqq 1$ を満たす$x,y$に対して
(1)$x^2+y^2-3x-2y$ の最大値、最小値とそのときの$x,y$を求めよ。
(2)$\displaystyle \frac{y}{x+2}$ の最大値、最小値とそのときの$x,y$を求めよ。
(3)$xy$ の最大値とそのときの$x,y$を求めよ。
この動画を見る
${\Large\boxed{1}}$ 不等式$-1 \leqq y-x \leqq 1,$ $-1 \leqq x+y \leqq 1$ を満たす$x,y$に対して
(1)$x^2+y^2-3x-2y$ の最大値、最小値とそのときの$x,y$を求めよ。
(2)$\displaystyle \frac{y}{x+2}$ の最大値、最小値とそのときの$x,y$を求めよ。
(3)$xy$ の最大値とそのときの$x,y$を求めよ。
福田の一夜漬け数学〜図形と方程式〜領域(3)領域における最大最小を本当に理解する、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 4つの不等式$x \geqq 0,y \geqq 0,2x+y \leqq 5,$$x+2y \leqq 4$を満たす$x,y$に対して
(1)$x+y$ の最大値、最小値とそのときの$x,y$を求めよ。
(2)$x+3y$ の最大値、最小値とそのときの$x,y$を求めよ。
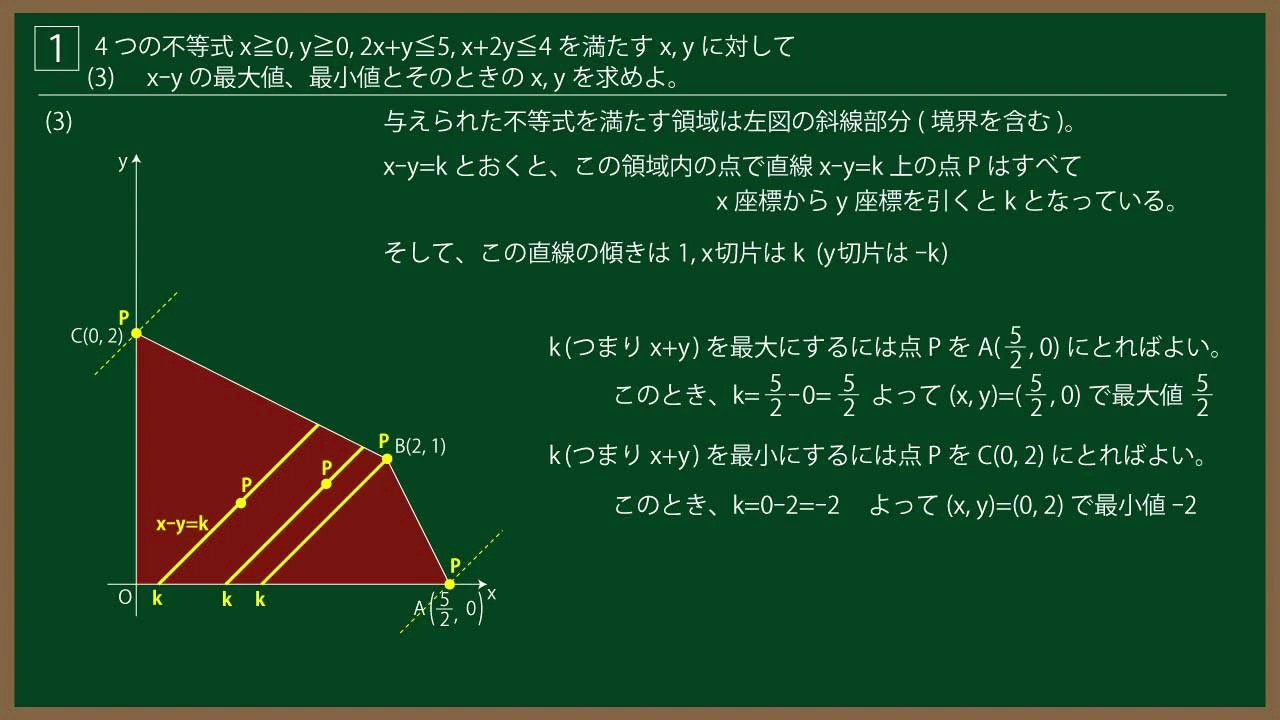
(3)$x-y$ の最大値、最小値とそのときの$x,y$を求めよ。
この動画を見る
${\Large\boxed{1}}$ 4つの不等式$x \geqq 0,y \geqq 0,2x+y \leqq 5,$$x+2y \leqq 4$を満たす$x,y$に対して
(1)$x+y$ の最大値、最小値とそのときの$x,y$を求めよ。
(2)$x+3y$ の最大値、最小値とそのときの$x,y$を求めよ。
(3)$x-y$ の最大値、最小値とそのときの$x,y$を求めよ。
福田の一夜漬け数学〜図形と方程式〜領域(2)複雑なな領域の図示、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
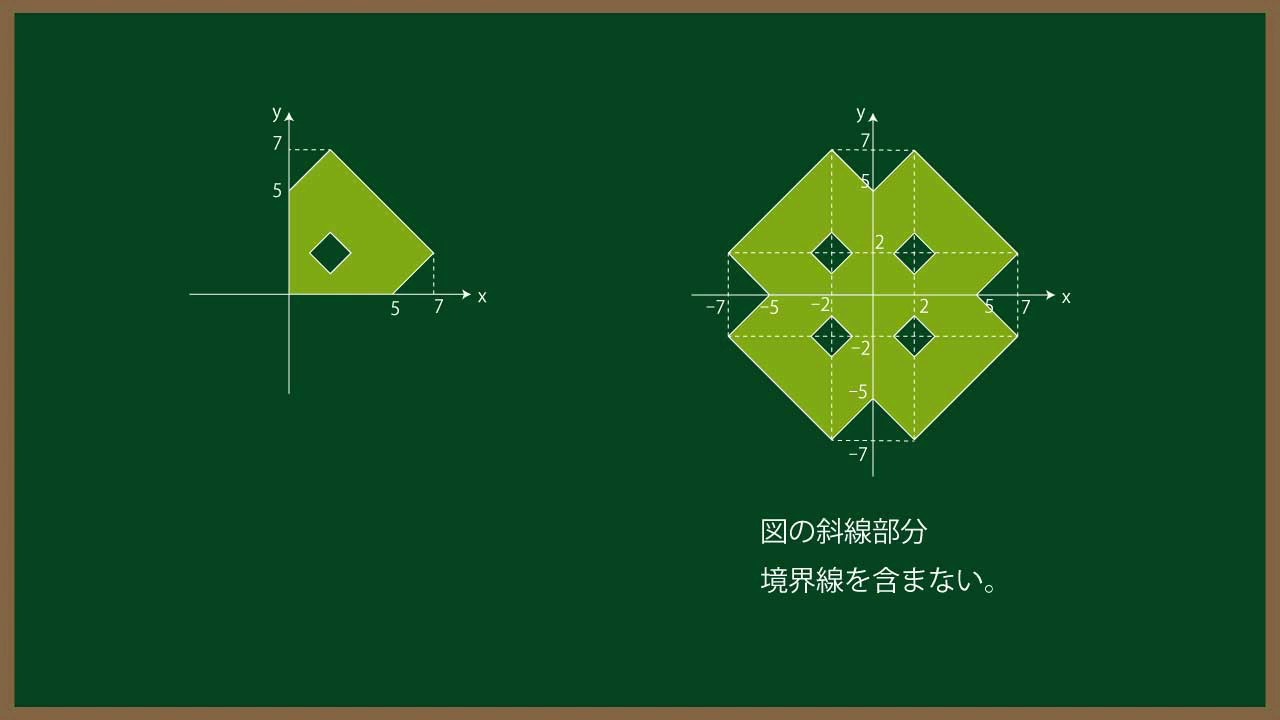
${\Large\boxed{1}}$ 次の領域を図示せよ。
$1 \lt ||x|-2|+||y|-2| \lt 5$ $\cdots$①
この動画を見る
${\Large\boxed{1}}$ 次の領域を図示せよ。
$1 \lt ||x|-2|+||y|-2| \lt 5$ $\cdots$①
福田の一夜漬け数学〜図形と方程式〜領域(1)基本的な領域の図示、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 次の領域を図示せよ。
(1)$y \gt \frac{1}{x}$
(2)$xy \gt 1$
(3)$\begin{eqnarray}
\left\{
\begin{array}{l}
y \gt 3x-5 \\
x^2+y^2 \lt 25
\end{array}
\right.
\end{eqnarray}$
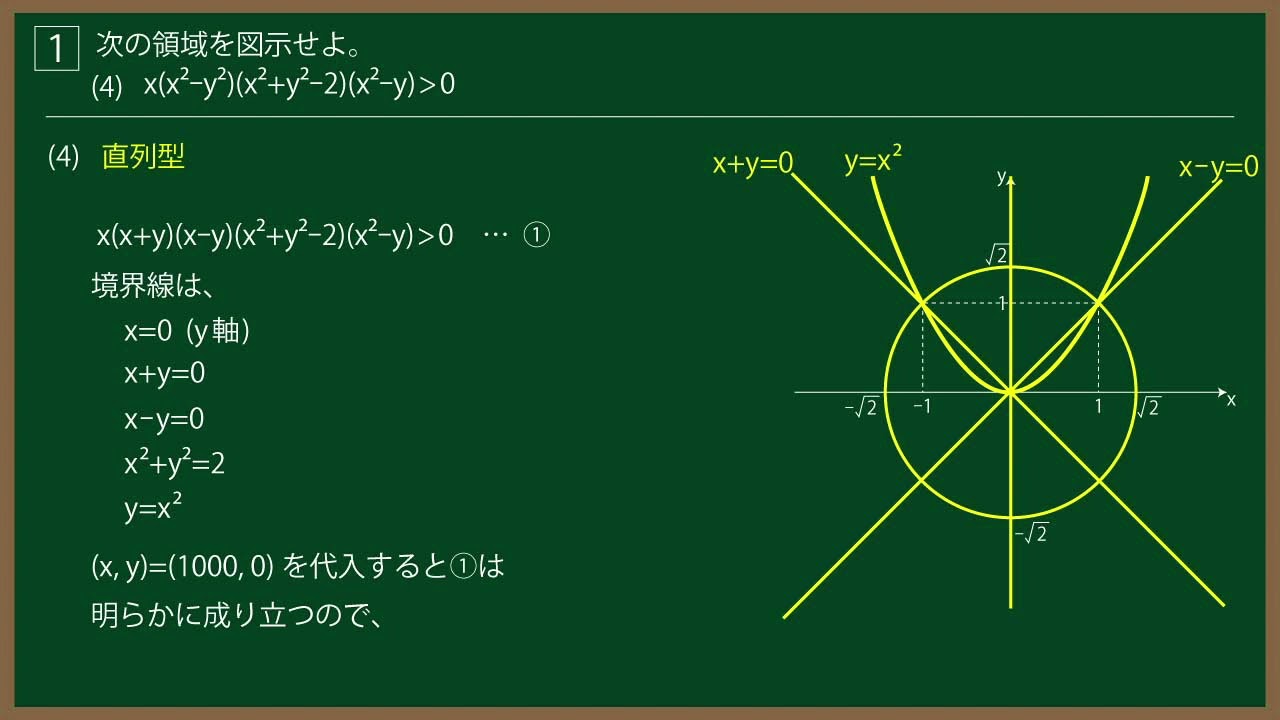
(4)$x(x^2-y^2)(x^2+y^2-2)$$(x^2-y) \gt 0$
(5)$|x|+|y| \leqq 1$
この動画を見る
${\Large\boxed{1}}$ 次の領域を図示せよ。
(1)$y \gt \frac{1}{x}$
(2)$xy \gt 1$
(3)$\begin{eqnarray}
\left\{
\begin{array}{l}
y \gt 3x-5 \\
x^2+y^2 \lt 25
\end{array}
\right.
\end{eqnarray}$
(4)$x(x^2-y^2)(x^2+y^2-2)$$(x^2-y) \gt 0$
(5)$|x|+|y| \leqq 1$
東京学芸大 不等式の範囲 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#東京学芸大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京学芸大学過去問題
x,yが$(2x-y-2)^2(x-y+1)\leqq 0$と$x^2+y^2<4$をみたすとき、y-xのとる値の範囲を求めよ。
この動画を見る
東京学芸大学過去問題
x,yが$(2x-y-2)^2(x-y+1)\leqq 0$と$x^2+y^2<4$をみたすとき、y-xのとる値の範囲を求めよ。
福田の一夜漬け数学〜図形と方程式〜軌跡(7)切り取られる弦の中点の軌跡(後編)、高校2年生

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 点$A(3,0)$を通る直線と円$(x-1)^2+y^2=1$ が異なる2点$P,Q$で
交わる時線分$PQ$の中点$M$の軌跡を求めよ。
この動画を見る
${\Large\boxed{1}}$ 点$A(3,0)$を通る直線と円$(x-1)^2+y^2=1$ が異なる2点$P,Q$で
交わる時線分$PQ$の中点$M$の軌跡を求めよ。
福田の一夜漬け数学〜図形と方程式〜軌跡(6)切り取られる弦の中点の軌跡(前編)、高校2年生

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 点$A(3,0)$を通る直線と円$(x-1)^2+y^2=1$ が異なる2点$P,Q$で
交わる時線分$PQ$の中点$M$の軌跡を求めよ。
この動画を見る
${\Large\boxed{1}}$ 点$A(3,0)$を通る直線と円$(x-1)^2+y^2=1$ が異なる2点$P,Q$で
交わる時線分$PQ$の中点$M$の軌跡を求めよ。
福田の一夜漬け数学〜図形と方程式〜軌跡(4)2直線の交点の軌跡、高校2年生
単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
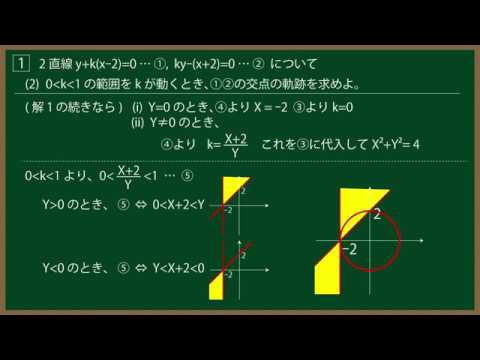
${\Large\boxed{1}}$ 2直線$y+k(x-2)=0$ $\cdots$①,$ky-(x+2)=0$ $\cdots$② について
(1)$k$が全ての実数値を取るとき、①②の交点の軌跡を求めよ。
(2)$0 \lt k \lt 1$の範囲をkが動くとき、①②の交点の軌跡を求めよ。
この動画を見る
${\Large\boxed{1}}$ 2直線$y+k(x-2)=0$ $\cdots$①,$ky-(x+2)=0$ $\cdots$② について
(1)$k$が全ての実数値を取るとき、①②の交点の軌跡を求めよ。
(2)$0 \lt k \lt 1$の範囲をkが動くとき、①②の交点の軌跡を求めよ。
福田の一夜漬け数学〜図形と方程式〜軌跡(5)動点が2個ある場合の軌跡、高校2年生

単元:
#数A#数Ⅱ#図形の性質#内心・外心・重心とチェバ・メネラウス#図形と方程式#点と直線#円と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 定点$A(2,0),B(4,0)$と円$C:x^2+y^2=9$ がある。
動点$P$が円$C$上を動くとき、$\triangle ABP$の重心$G$の軌跡を求めよ。
この動画を見る
${\Large\boxed{1}}$ 定点$A(2,0),B(4,0)$と円$C:x^2+y^2=9$ がある。
動点$P$が円$C$上を動くとき、$\triangle ABP$の重心$G$の軌跡を求めよ。
早稲田 学習院 高校数学 Mathematics Japanese university entrance exam

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
学習院大学過去問題
$x^3+y^3=3xy$ (x,y実数)
x+yのとりうる範囲
早稲田大学過去問題
$a_1$~$a_n$整数
$x^n+a_1x^{n-1}+a_2x^{n-2}+\cdots+a_{n-1}x+a_n=0$
整数係数のn次方程式、解が有理数ならその解は整数である。
この動画を見る
学習院大学過去問題
$x^3+y^3=3xy$ (x,y実数)
x+yのとりうる範囲
早稲田大学過去問題
$a_1$~$a_n$整数
$x^n+a_1x^{n-1}+a_2x^{n-2}+\cdots+a_{n-1}x+a_n=0$
整数係数のn次方程式、解が有理数ならその解は整数である。
福田の一夜漬け数学〜図形と方程式〜軌跡(3)媒介変数表示の点、高校2年生

単元:
#数Ⅱ#平面上の曲線#図形と方程式#軌跡と領域#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 次の媒介変数表示で表された点$P(x,y)$の軌跡を求めよ。
(1)$x=\displaystyle \frac{\cos\theta+\sin\theta}{\sqrt2},$ $y=\displaystyle \frac{\cos\theta-\sin\theta}{\sqrt2}$ ($\theta$は任意の実数)
(2)$x=\displaystyle \frac{1-t^2}{1+t^2},$ $y=\displaystyle \frac{2t}{1+t^2}$ ($t$は任意の実数)
この動画を見る
${\Large\boxed{1}}$ 次の媒介変数表示で表された点$P(x,y)$の軌跡を求めよ。
(1)$x=\displaystyle \frac{\cos\theta+\sin\theta}{\sqrt2},$ $y=\displaystyle \frac{\cos\theta-\sin\theta}{\sqrt2}$ ($\theta$は任意の実数)
(2)$x=\displaystyle \frac{1-t^2}{1+t^2},$ $y=\displaystyle \frac{2t}{1+t^2}$ ($t$は任意の実数)
福田の一夜漬け数学〜図形と方程式〜軌跡(2)アポロニウスの円、高校2年生

単元:
#数Ⅱ#図形と方程式#点と直線#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 2点$A(2,3),B(6,1)$がある。次の条件を満たす点$P,Q$の軌跡を求めよ。
(1)$2$点$A,B$からの距離が等しい点$P$
(2)$2$点$A,B$からの距離の比が$1:3$である点$Q$
この動画を見る
${\Large\boxed{1}}$ 2点$A(2,3),B(6,1)$がある。次の条件を満たす点$P,Q$の軌跡を求めよ。
(1)$2$点$A,B$からの距離が等しい点$P$
(2)$2$点$A,B$からの距離の比が$1:3$である点$Q$
福田の一夜漬け数学〜図形と方程式〜軌跡(1)軌跡の鉄則、高校2年生

単元:
#数Ⅰ#数Ⅱ#2次関数#2次関数とグラフ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 放物線$y=x^2-2(a+1)x+2a$ $\cdots$①の頂点を$P$とする。$a$が$1$より大きい
実数を動くとき、点Pの軌跡を求めよ。
この動画を見る
${\Large\boxed{1}}$ 放物線$y=x^2-2(a+1)x+2a$ $\cdots$①の頂点を$P$とする。$a$が$1$より大きい
実数を動くとき、点Pの軌跡を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(13)放物線と円の位置関係、高校2年生
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
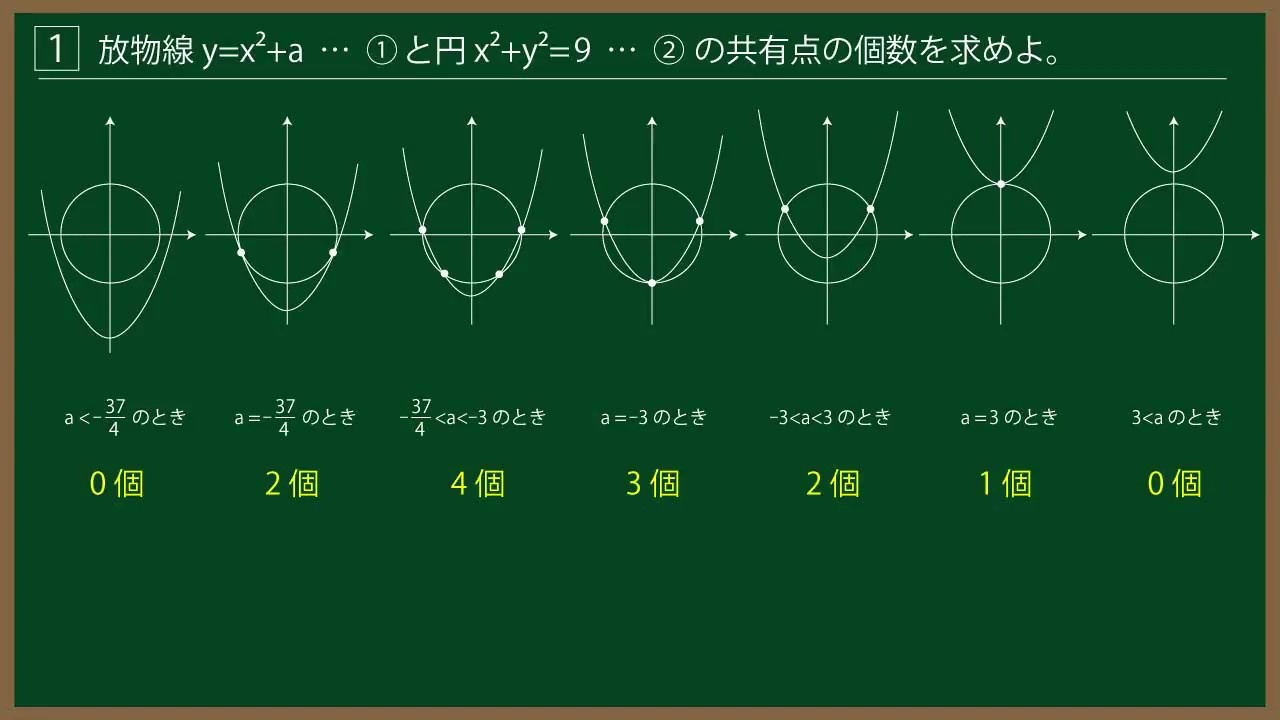
${\Large\boxed{1}}$ 放物線$y=x^2+a$ $\cdots$①と円$x^2+y^2=9$ $\cdots$②の共有点の個数を求めよ。
この動画を見る
${\Large\boxed{1}}$ 放物線$y=x^2+a$ $\cdots$①と円$x^2+y^2=9$ $\cdots$②の共有点の個数を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(12)共通接線、高校2年生

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 2つの円$x^2+y^2=4$ $\cdots$①と$(x-4)^2+y^2=1$ $\cdots$②
の共通接線を全て求めよ。
この動画を見る
${\Large\boxed{1}}$ 2つの円$x^2+y^2=4$ $\cdots$①と$(x-4)^2+y^2=1$ $\cdots$②
の共通接線を全て求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(11)円群と共通弦、高校2年生

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 2つの円$x^2+y^2=4$ $\cdots$①と$x^2+y^2+4x-2y+4=0$ $\cdots$②について、
(1)2つの円は、異なる2点で交わることを示せ。
(2)2つの円の交点を通る直線の方程式を求めよ。
(3)2つの円の交点と原点を通る円の方程式を求めよ。
${\Large\boxed{2}}$ 中心$(a,b),$半径2の円と円$x^2+y^2=9$ $\cdots$①との2つの共有点を通る直線
の方程式が$6x-2y-15=0$となるような点$(a,b)$を求めよ。
この動画を見る
${\Large\boxed{1}}$ 2つの円$x^2+y^2=4$ $\cdots$①と$x^2+y^2+4x-2y+4=0$ $\cdots$②について、
(1)2つの円は、異なる2点で交わることを示せ。
(2)2つの円の交点を通る直線の方程式を求めよ。
(3)2つの円の交点と原点を通る円の方程式を求めよ。
${\Large\boxed{2}}$ 中心$(a,b),$半径2の円と円$x^2+y^2=9$ $\cdots$①との2つの共有点を通る直線
の方程式が$6x-2y-15=0$となるような点$(a,b)$を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(10)2円の位置関係、高校2年生

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 2つの円$x^2+y^2=10$ $\cdots$①, $x^2+y^2-2ax-6ay$$+40a-50=0$ $\cdots$②
が接するように、定数aの値を求めよ。
この動画を見る
${\Large\boxed{1}}$ 2つの円$x^2+y^2=10$ $\cdots$①, $x^2+y^2-2ax-6ay$$+40a-50=0$ $\cdots$②
が接するように、定数aの値を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(9)外から引いた接線(中心が原点以外の場合)、高校2年生

単元:
#数Ⅱ#複素数と方程式#図形と方程式#解と判別式・解と係数の関係#点と直線#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 円$(x+2)^2+(y-2)^2=10$ の接線で、点(2,4)を通るものを求めよ。
また、接点の座標を求めよ。
この動画を見る
${\Large\boxed{1}}$ 円$(x+2)^2+(y-2)^2=10$ の接線で、点(2,4)を通るものを求めよ。
また、接点の座標を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(8)外から引いた接線(原点中心の円の場合)、高校2年生

単元:
#数Ⅱ#複素数と方程式#図形と方程式#解と判別式・解と係数の関係#点と直線#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 円$x^2+y^2=5$ の接線で、点(3,1)を通るものを求めよ。
また、接点の座標を求めよ。
この動画を見る
${\Large\boxed{1}}$ 円$x^2+y^2=5$ の接線で、点(3,1)を通るものを求めよ。
また、接点の座標を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(7)接線の公式と極線の公式、高校2年生

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (1)円$x^2+y^2=25$ 上の点$(-4,3)$における接線の方程式を求めよ。
(2)円$x^2+y^2-2x+6y=0$ 上の点$(2,-6)$における接線の方程式を求めよ。
(3)円$x^2+y^2=25$ $\cdots$①の外部の点$A(3,8)$から円①に2本の接線を引き、
その2つの接点を$P,Q$とする。直線$PQ$の方程式を求めよ。
この動画を見る
${\Large\boxed{1}}$ (1)円$x^2+y^2=25$ 上の点$(-4,3)$における接線の方程式を求めよ。
(2)円$x^2+y^2-2x+6y=0$ 上の点$(2,-6)$における接線の方程式を求めよ。
(3)円$x^2+y^2=25$ $\cdots$①の外部の点$A(3,8)$から円①に2本の接線を引き、
その2つの接点を$P,Q$とする。直線$PQ$の方程式を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(6)切り取られる弦の長さと中点(応用2)、高校2年生

単元:
#数Ⅱ#複素数と方程式#図形と方程式#解と判別式・解と係数の関係#円と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 円$x^2+y^2=4$ $\cdots$①, 直線$y=m(x-4)$ $\cdots$②がある。次の問いに答えよ。
(1)①②が異なる2点で交わるように定数$m$の値の範囲を求めよ。
(2)(1)のとき、②が①によって切り取られる弦の中点の座標を$m$を用いて表せ。
(3)(1)で求めた範囲を$m$が動くとき、(2)の中点はどんな図形を描くか。
この動画を見る
${\Large\boxed{1}}$ 円$x^2+y^2=4$ $\cdots$①, 直線$y=m(x-4)$ $\cdots$②がある。次の問いに答えよ。
(1)①②が異なる2点で交わるように定数$m$の値の範囲を求めよ。
(2)(1)のとき、②が①によって切り取られる弦の中点の座標を$m$を用いて表せ。
(3)(1)で求めた範囲を$m$が動くとき、(2)の中点はどんな図形を描くか。
福田の一夜漬け数学〜図形と方程式〜円の方程式(5)切り取られる弦の長さと中点(応用1)、高校2年生

単元:
#数Ⅱ#複素数と方程式#図形と方程式#解と判別式・解と係数の関係#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 円$x^2+y^2-4x+2y-4=0$ $\cdots$①が直線$x+2y+k=0$ $\cdots$②
から切り取る弦の長さが4であるとき、定数$k$の値を求めよ。
${\Large\boxed{2}}$ 直線$\ell:y=2x+a$ が放物線$C:y=x^2$ によって切り取られる弦
の長さが10となるように定数$a$の値を求めよ。
この動画を見る
${\Large\boxed{1}}$ 円$x^2+y^2-4x+2y-4=0$ $\cdots$①が直線$x+2y+k=0$ $\cdots$②
から切り取る弦の長さが4であるとき、定数$k$の値を求めよ。
${\Large\boxed{2}}$ 直線$\ell:y=2x+a$ が放物線$C:y=x^2$ によって切り取られる弦
の長さが10となるように定数$a$の値を求めよ。
