 三角関数とグラフ
三角関数とグラフ
 三角関数とグラフ
三角関数とグラフ
福田の数学〜明治大学2021年理工学部第1問(2)〜三角関数の最大最小

単元:
#数Ⅱ#三角関数#三角関数とグラフ#加法定理とその応用#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)座標平面上に2点$A(\frac{5}{8},0),\ B(0,\frac{3}{2})$をとる。Lは原点を通る直線で、Lが
x軸の正の方向となす角$\thetaは0 \leqq \theta \leqq \frac{\pi}{2}$の範囲にあるとする。ただし、角$\theta$の
符号は時計の針の回転と逆の向きを正の方向とする。点Aと直線Lとの距離を
$d_A$、点Bと直線Lの距離を$d_B$とおく。このとき、
$d_A+d_B=\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}\sin\theta+\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\cos\theta$
である。$\theta$が$0 \leqq \theta \leqq \frac{\pi}{2}$の範囲を動くとき、
$d_A+d_B$の最大値は$\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
最小値は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(2)座標平面上に2点$A(\frac{5}{8},0),\ B(0,\frac{3}{2})$をとる。Lは原点を通る直線で、Lが
x軸の正の方向となす角$\thetaは0 \leqq \theta \leqq \frac{\pi}{2}$の範囲にあるとする。ただし、角$\theta$の
符号は時計の針の回転と逆の向きを正の方向とする。点Aと直線Lとの距離を
$d_A$、点Bと直線Lの距離を$d_B$とおく。このとき、
$d_A+d_B=\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}\sin\theta+\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\cos\theta$
である。$\theta$が$0 \leqq \theta \leqq \frac{\pi}{2}$の範囲を動くとき、
$d_A+d_B$の最大値は$\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
最小値は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。
2021明治大学理工学部過去問
福田のわかった数学〜高校3年生理系077〜極値(1)極大値をもつ条件

単元:
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
この動画を見る
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
関数の問題にみえて実は。。新田高校
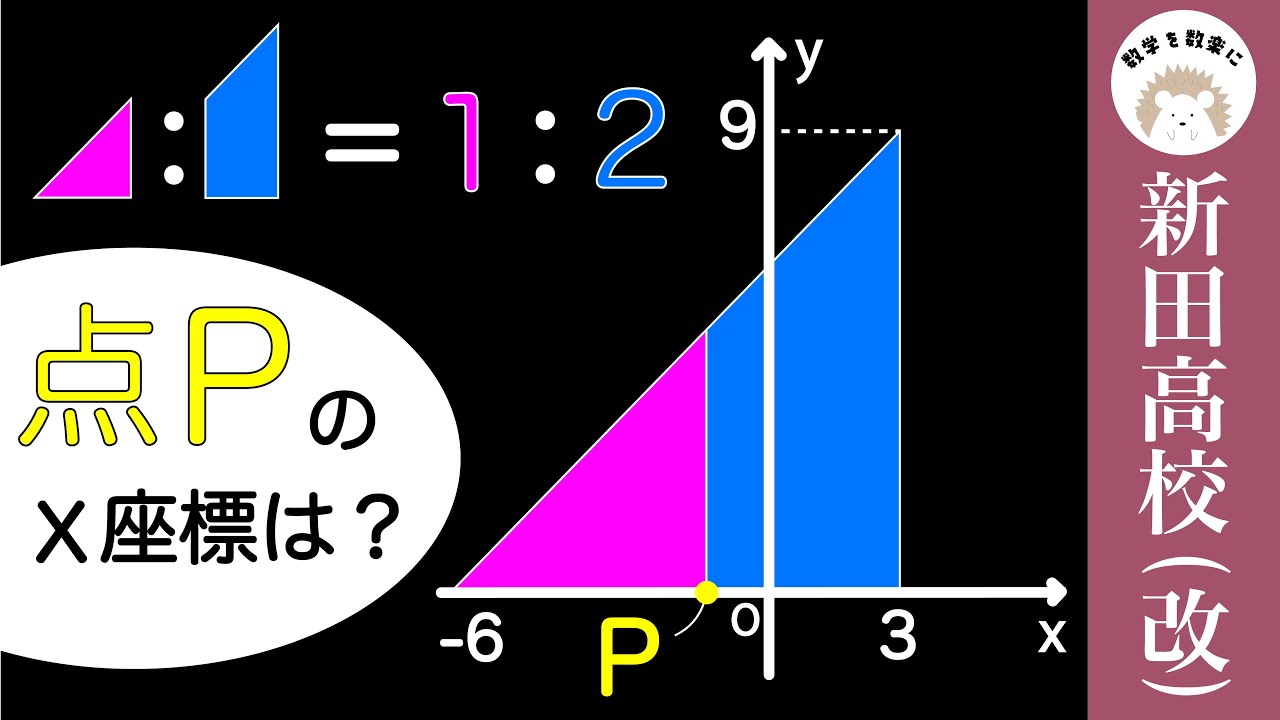
単元:
#数学(中学生)#数Ⅱ#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Pの座標は?
*図は動画内参照
新田高等学校
この動画を見る
点Pの座標は?
*図は動画内参照
新田高等学校
福田の数学〜中央大学2021年経済学部第1問(3)〜三角関数の最大

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}} (3)-\frac{\pi}{2} \leqq x \leqq \frac{\pi}{2}$
のとき、次の関数が最大値をとるときのxの値を求めよ。
$y=\sin x+\cos^2x$
2021中央大経済学部過去問
この動画を見る
${\Large\boxed{1}} (3)-\frac{\pi}{2} \leqq x \leqq \frac{\pi}{2}$
のとき、次の関数が最大値をとるときのxの値を求めよ。
$y=\sin x+\cos^2x$
2021中央大経済学部過去問
13和歌山県教員採用試験(数学:3番 三角関数)
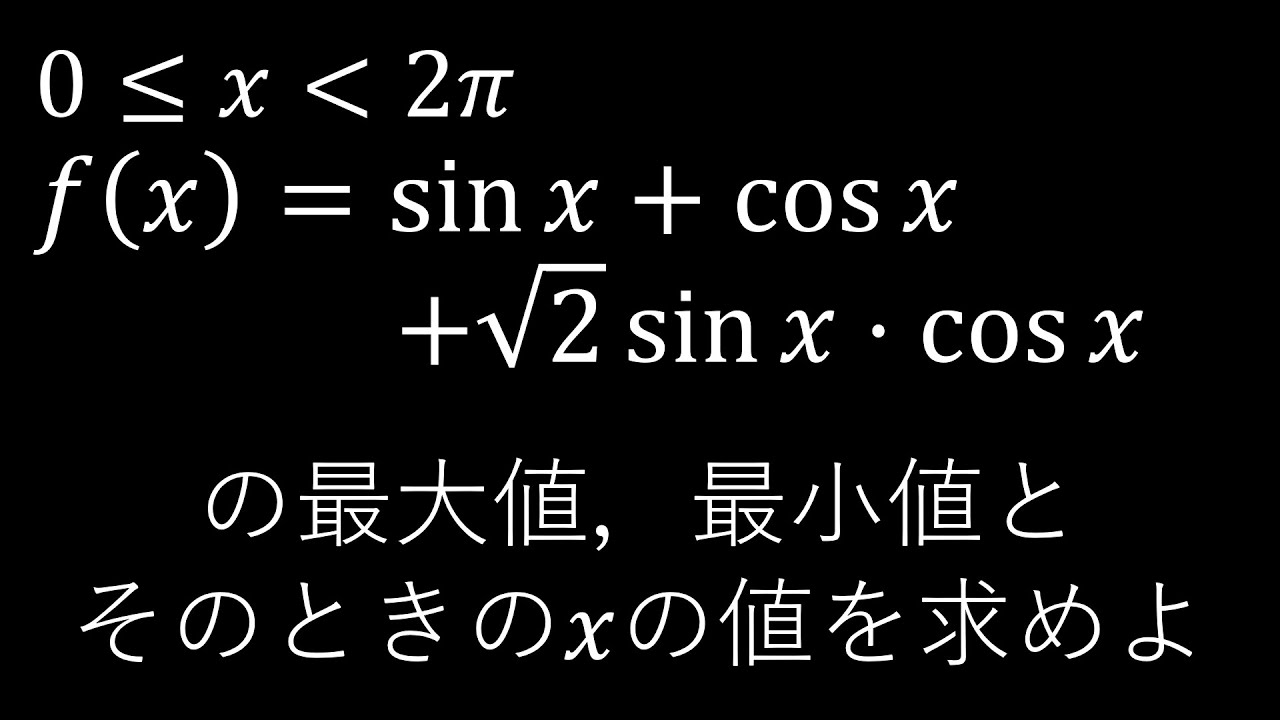
単元:
#数Ⅱ#三角関数#三角関数とグラフ#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$0\leqq x\lt 2\pi$である.
$f(x)=\sin x+\cos x+\sqrt 2 \sin x \cos x$の
最大値,最小値とそのときの$x$の値を求めよ.
この動画を見る
$\boxed{3}$
$0\leqq x\lt 2\pi$である.
$f(x)=\sin x+\cos x+\sqrt 2 \sin x \cos x$の
最大値,最小値とそのときの$x$の値を求めよ.
福田の数学〜慶應義塾大学2021年看護医療学部第1問(2)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#図形と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(2)$2(\cos\theta-\sin\theta)^2=1$を満たす$\theta$を$0 \leqq \theta \leqq \pi$の範囲で求めると$\boxed{\ \ イ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$
(2)$2(\cos\theta-\sin\theta)^2=1$を満たす$\theta$を$0 \leqq \theta \leqq \pi$の範囲で求めると$\boxed{\ \ イ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2021年薬学部第1問(4)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#図形と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(4)$\theta$は実数で、$-\frac{\pi}{2} \leqq \theta \leqq \frac{\pi}{2}$を満たす。方程式
$4\cos\frac{\theta}{2}(\cos\frac{\theta}{2}+\sin\frac{\theta}{2})=1$
を満たすとき、$\sin\theta+\cos\theta$の値は$\boxed{\ \ カ\ \ }$であり、
$\sin\theta$の値は$\boxed{\ \ キ\ \ }$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{1}}$(4)$\theta$は実数で、$-\frac{\pi}{2} \leqq \theta \leqq \frac{\pi}{2}$を満たす。方程式
$4\cos\frac{\theta}{2}(\cos\frac{\theta}{2}+\sin\frac{\theta}{2})=1$
を満たすとき、$\sin\theta+\cos\theta$の値は$\boxed{\ \ カ\ \ }$であり、
$\sin\theta$の値は$\boxed{\ \ キ\ \ }$である。
2021慶應義塾大学薬学部過去問
【高校数学】三角関数のグラフの裏技~平行移動の場合~【数学Ⅱ】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
グラフを書け
1⃣
$y=\sin \theta+1$
2⃣
$y=2\sin(2\theta-\displaystyle \frac{\pi}{3})+1$
この動画を見る
グラフを書け
1⃣
$y=\sin \theta+1$
2⃣
$y=2\sin(2\theta-\displaystyle \frac{\pi}{3})+1$
【高校数学】三角関数の性質の裏技~先生には怒られるかもしれません~ 4-3.5【数学Ⅱ】

【数Ⅱ】三角関数:置換したときの解の個数を考える

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#チャート式#黄チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0\leqq\theta\lt2\pi$のとき、$\sin^2\theta-\sin\theta=a$ この方程式の解の個数を実数aの値で場合分けして求めよ
この動画を見る
$0\leqq\theta\lt2\pi$のとき、$\sin^2\theta-\sin\theta=a$ この方程式の解の個数を実数aの値で場合分けして求めよ
【高校数学】象限と三角関数の符号の関係 4-2【数学Ⅱ】
【数Ⅱ】三角関数:解が三角関数で表される2次方程式:p>0とする。xの方程式4x²+2(1-p)x-p=0の解が、sinθとcosθ(0≦θ<2π)であるとき、pとθの値を求めよう。

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
解が三角関数で表される2次方程式:p>0とする。xの方程式$4x^2+2(1-p)x-p=0$の解が、$sinθ$と$cosθ(0≦θ<2\pi)$であるとき、$p$と$\theta$の値を求めよう。
この動画を見る
解が三角関数で表される2次方程式:p>0とする。xの方程式$4x^2+2(1-p)x-p=0$の解が、$sinθ$と$cosθ(0≦θ<2\pi)$であるとき、$p$と$\theta$の値を求めよう。
2021東大 円と3次関数の共有点

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=ax^3-2x$と原点が中心で半径$1$の円と$6$つの共有点をもつ$a$の範囲を求めよ.$(a\gt 0)$
2021東大過去問
この動画を見る
$y=ax^3-2x$と原点が中心で半径$1$の円と$6$つの共有点をもつ$a$の範囲を求めよ.$(a\gt 0)$
2021東大過去問
【数Ⅱ】三角関数:関数y=-sin²θ+cosθ(0≦θ<2π)の最大値と最小値を求めよう。その時のθも求めよう。

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$y=-\sin^2\theta+\cos\theta(0≦\theta<2\pi)$の最大値と最小値を求めよう。その時の$\theta$も求めよう。
この動画を見る
関数$y=-\sin^2\theta+\cos\theta(0≦\theta<2\pi)$の最大値と最小値を求めよう。その時の$\theta$も求めよう。
産業医科大 cos sin 和の値

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=\Box$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=\Box$
2019産業医大過去問
この動画を見る
これを解け.
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=\Box$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=\Box$
2019産業医大過去問
コメント欄はありがたい。本当に2秒で答えが出た

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
この動画を見る
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
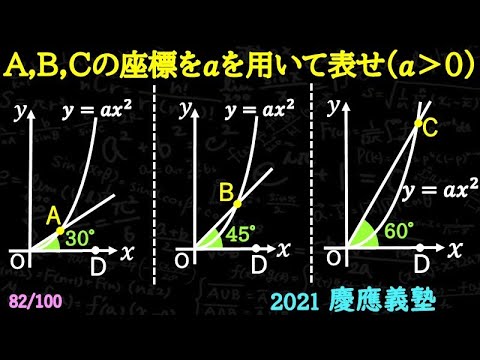
30度 45度 60度の直線の式 A 慶應義塾 2021
単元:
#数学(中学生)#数Ⅱ#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
A,B,Cの座標をaを用いて表せ
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
A,B,Cの座標をaを用いて表せ
*図は動画内参照
2021慶應義塾高等学校
瞬殺!!関数の典型問題 A 2021 秋田県

共通テスト第2日程2021年数学詳しい解説〜共通テスト第2日程2021年2B第1問〜対数関数と三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#指数関数と対数関数#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1] (1)$\log_{10}10=\boxed{\ \ ア\ \ }$である。また、$\log_{10}5,\log_{10}15$をそれぞれ
$\log_{10}2と\log_{10}3$を用いて表すと
$\log_{10}5=\boxed{\ \ イ\ \ }\log_{10}2+\boxed{\ \ ウ\ \ }$
$\log_{10}15=$$\boxed{\ \ エ\ \ }\log_{10}2+\log_{10}3+\boxed{\ \ オ\ \ }$
(2)太郎さんと花子さんは、$15^{20}$について話している。
以下では、$\log_{10}2=0.3010、$$\log_{10}3=0.4771$とする。
太郎:$15^{20}$は何桁の数だろう。
花子:$15$の20乗を求めるのは大変だね。$\log_{10}15^{20}$の整数部分に
着目してみようよ。
$\log_{10}15^{20}$は
$\boxed{\ \ カキ\ \ } \lt \log_{10}15^{20}$$ \lt \boxed{\ \ カキ\ \ }+1$
を満たす。よって、$15^{20}は\boxed{\ \ クケ\ \ }$桁の数である。
太郎:$15^{20}$の最高位の数字も知りたいね。だけど、$\log_{10}15^{20}$の
整数部分にだけ着目してもわからないな。
花子:$N・10^{\boxed{カキ}} \lt 15^{20}$$ \lt (N+1)・10^{\boxed{カキ}}$を満たすような
正の整数Nに着目してみたらどうかな。
$\log_{10}15^{20}$の小数部分は$\log_{10}15^{20}-\boxed{\ \ カキ\ \ }$であり
$\log_{10}\boxed{\ \ コ\ \ } \lt \log_{10}15^{20}-\boxed{\ \ カキ\ \ }$$ \lt \log_{10}(\boxed{\ \ コ\ \ }+1)$
が成り立つので、$15^{20}$の最高位の数字は$\boxed{\ \ サ\ \ }$である。
[2]座標平面上の原点を中心とする半径1の円周上に3点$P(\cos\theta,\sin\theta),$
$Q(\cos\alpha,\sin\alpha),R(\cos\beta,\sin\beta)$がある。ただし、$0 \leqq \theta \lt \alpha \lt \beta \lt 2\pi$
とする。このとき、$s$と$t$を次のように定める。
$s=\cos\theta+\cos\alpha+\cos\beta,$$ t=\sin\theta+\sin\alpha+\sin\beta$
(1)$\triangle PQR$が正三角形や二等辺三角形のときの$s$と$t$の値について考察しよう。
考察$1:\triangle PQR$が正三角形である場合を考える。
この場合、$\alpha,\beta$を$\theta$で表すと
$\alpha=\theta+\displaystyle \frac{\boxed{\ \ シ\ \ }}{3}\pi,$$ \beta=\theta+\displaystyle \frac{\boxed{\ \ ス\ \ }}{3}\pi$
であり、加法定理により
$\cos\alpha=\boxed{\boxed{\ \ セ\ \ }}, \sin\alpha=\boxed{\boxed{\ \ ソ\ \ }}$
である。同様に、$\cos\beta$および$\sin\beta$を、$\sin\theta$と$\cos\theta$を用いて表すことができる。
これらのことから、$s=t=\boxed{\ \ タ\ \ }$である。
$\boxed{\boxed{\ \ セ\ \ }},\boxed{\boxed{\ \ ソ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\displaystyle \frac{1}{2}\sin\theta+\displaystyle \frac{\sqrt3}{2}\cos\theta$
①$\displaystyle \frac{\sqrt3}{2}\sin\theta+\displaystyle \frac{1}{2}\cos\theta$
②$\displaystyle \frac{1}{2}\sin\theta-\displaystyle \frac{\sqrt3}{2}\cos\theta$
③$\displaystyle \frac{\sqrt3}{2}\sin\theta-\displaystyle \frac{1}{2}\cos\theta$
④$-\displaystyle \frac{1}{2}\sin\theta+\displaystyle \frac{\sqrt3}{2}\cos\theta$
⑤$-\displaystyle \frac{\sqrt3}{2}\sin\theta+\displaystyle \frac{1}{2}\cos\theta$
②$-\displaystyle \frac{1}{2}\sin\theta-\displaystyle \frac{\sqrt3}{2}\cos\theta$
③$-\displaystyle \frac{\sqrt3}{2}\sin\theta-\displaystyle \frac{1}{2}\cos\theta$
考察2:$\triangle PQR$が$PQ=PR$となる二等辺三角形である場合を考える。
例えば、点$P$が直線$y=x$上にあり、点$Q,R$が直線$y=x$に関して対称
であるときを考える。このとき、$\theta=\displaystyle \frac{\pi}{4}$である。また、$\alpha$は
$\alpha \lt \displaystyle \frac{5}{4}\pi, \beta$は$\displaystyle \frac{5}{4}\pi \lt \beta$を満たし、点$Q,R$の座標について、
$\sin\beta=\cos\alpha, \cos\beta=\sin\alpha$が成り立つ。よって
$s=t=\displaystyle \frac{\sqrt{\boxed{\ \ チ\ \ }}}{\boxed{\ \ ツ\ \ }}+\sin\alpha+\cos\alpha$
である。
ここで、三角関数の合成により
$\sin\alpha+\cos\alpha=$$\sqrt{\boxed{\ \ テ\ \ }}\sin\left(\alpha+\displaystyle \frac{\pi}{\boxed{\ \ ト\ \ }}\right)$
である。したがって
$\alpha=\displaystyle \frac{\boxed{\ \ ナニ\ \ }}{12}\pi, \beta=\displaystyle \frac{\boxed{\ \ ヌネ\ \ }}{12}\pi$
のとき、$s=t=0$である。
(2)次に、$s$と$t$の値を定めるときの$\theta,\alpha,\beta$の関係について考察しよう。
考察$3:s=t=0$の場合を考える。
この場合、$\sin^2\theta+\cos^2\theta=1$により、$\alpha$と$\beta$について考えると
$\cos\alpha\cos\beta+\sin\alpha\sin\beta=\displaystyle \frac{\boxed{\ \ ノハ\ \ }}{\boxed{\ \ ヒ\ \ }}$
である。
同様に、$\theta$と$\alpha$について考えると
$\cos\theta\cos\alpha+\sin\theta\sin\alpha=\displaystyle \frac{\boxed{\ \ ノハ\ \ }}{\boxed{\ \ ヒ\ \ }}$
であるから、$\theta,\alpha,\beta$の範囲に注意すると
$\beta-\alpha=\alpha-\theta=\displaystyle \frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}\pi$
という関係が得られる。
(3)これまでの考察を振り返ると、次の⓪~③のうち、
正しいものは$\boxed{\boxed{\ \ ホ\ \ }}$であることが分かる。
$\boxed{\boxed{\ \ ホ\ \ }}$の解答群
⓪$\triangle PQR$が正三角形ならば$s=t=0$であり、$s=t=0$ならば
$\triangle PQR$は正三角形である。
①$\triangle PQR$が正三角形ならば$s=t=0$であり、$s=t=0$で
あっても$\triangle PQR$は正三角形でない場合がある。
②$\triangle PQR$が正三角形であっても$s=t=0$でない場合があるが
$s=t=0$ならば$\triangle PQR$は正三角形である。
③$\triangle PQR$が正三角形であっても$s=t=0$でない場合があり、
$s=t=0$であっても$\triangle PQR$が正三角形でない場合がある。
この動画を見る
${\large第1問}$
[1] (1)$\log_{10}10=\boxed{\ \ ア\ \ }$である。また、$\log_{10}5,\log_{10}15$をそれぞれ
$\log_{10}2と\log_{10}3$を用いて表すと
$\log_{10}5=\boxed{\ \ イ\ \ }\log_{10}2+\boxed{\ \ ウ\ \ }$
$\log_{10}15=$$\boxed{\ \ エ\ \ }\log_{10}2+\log_{10}3+\boxed{\ \ オ\ \ }$
(2)太郎さんと花子さんは、$15^{20}$について話している。
以下では、$\log_{10}2=0.3010、$$\log_{10}3=0.4771$とする。
太郎:$15^{20}$は何桁の数だろう。
花子:$15$の20乗を求めるのは大変だね。$\log_{10}15^{20}$の整数部分に
着目してみようよ。
$\log_{10}15^{20}$は
$\boxed{\ \ カキ\ \ } \lt \log_{10}15^{20}$$ \lt \boxed{\ \ カキ\ \ }+1$
を満たす。よって、$15^{20}は\boxed{\ \ クケ\ \ }$桁の数である。
太郎:$15^{20}$の最高位の数字も知りたいね。だけど、$\log_{10}15^{20}$の
整数部分にだけ着目してもわからないな。
花子:$N・10^{\boxed{カキ}} \lt 15^{20}$$ \lt (N+1)・10^{\boxed{カキ}}$を満たすような
正の整数Nに着目してみたらどうかな。
$\log_{10}15^{20}$の小数部分は$\log_{10}15^{20}-\boxed{\ \ カキ\ \ }$であり
$\log_{10}\boxed{\ \ コ\ \ } \lt \log_{10}15^{20}-\boxed{\ \ カキ\ \ }$$ \lt \log_{10}(\boxed{\ \ コ\ \ }+1)$
が成り立つので、$15^{20}$の最高位の数字は$\boxed{\ \ サ\ \ }$である。
[2]座標平面上の原点を中心とする半径1の円周上に3点$P(\cos\theta,\sin\theta),$
$Q(\cos\alpha,\sin\alpha),R(\cos\beta,\sin\beta)$がある。ただし、$0 \leqq \theta \lt \alpha \lt \beta \lt 2\pi$
とする。このとき、$s$と$t$を次のように定める。
$s=\cos\theta+\cos\alpha+\cos\beta,$$ t=\sin\theta+\sin\alpha+\sin\beta$
(1)$\triangle PQR$が正三角形や二等辺三角形のときの$s$と$t$の値について考察しよう。
考察$1:\triangle PQR$が正三角形である場合を考える。
この場合、$\alpha,\beta$を$\theta$で表すと
$\alpha=\theta+\displaystyle \frac{\boxed{\ \ シ\ \ }}{3}\pi,$$ \beta=\theta+\displaystyle \frac{\boxed{\ \ ス\ \ }}{3}\pi$
であり、加法定理により
$\cos\alpha=\boxed{\boxed{\ \ セ\ \ }}, \sin\alpha=\boxed{\boxed{\ \ ソ\ \ }}$
である。同様に、$\cos\beta$および$\sin\beta$を、$\sin\theta$と$\cos\theta$を用いて表すことができる。
これらのことから、$s=t=\boxed{\ \ タ\ \ }$である。
$\boxed{\boxed{\ \ セ\ \ }},\boxed{\boxed{\ \ ソ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\displaystyle \frac{1}{2}\sin\theta+\displaystyle \frac{\sqrt3}{2}\cos\theta$
①$\displaystyle \frac{\sqrt3}{2}\sin\theta+\displaystyle \frac{1}{2}\cos\theta$
②$\displaystyle \frac{1}{2}\sin\theta-\displaystyle \frac{\sqrt3}{2}\cos\theta$
③$\displaystyle \frac{\sqrt3}{2}\sin\theta-\displaystyle \frac{1}{2}\cos\theta$
④$-\displaystyle \frac{1}{2}\sin\theta+\displaystyle \frac{\sqrt3}{2}\cos\theta$
⑤$-\displaystyle \frac{\sqrt3}{2}\sin\theta+\displaystyle \frac{1}{2}\cos\theta$
②$-\displaystyle \frac{1}{2}\sin\theta-\displaystyle \frac{\sqrt3}{2}\cos\theta$
③$-\displaystyle \frac{\sqrt3}{2}\sin\theta-\displaystyle \frac{1}{2}\cos\theta$
考察2:$\triangle PQR$が$PQ=PR$となる二等辺三角形である場合を考える。
例えば、点$P$が直線$y=x$上にあり、点$Q,R$が直線$y=x$に関して対称
であるときを考える。このとき、$\theta=\displaystyle \frac{\pi}{4}$である。また、$\alpha$は
$\alpha \lt \displaystyle \frac{5}{4}\pi, \beta$は$\displaystyle \frac{5}{4}\pi \lt \beta$を満たし、点$Q,R$の座標について、
$\sin\beta=\cos\alpha, \cos\beta=\sin\alpha$が成り立つ。よって
$s=t=\displaystyle \frac{\sqrt{\boxed{\ \ チ\ \ }}}{\boxed{\ \ ツ\ \ }}+\sin\alpha+\cos\alpha$
である。
ここで、三角関数の合成により
$\sin\alpha+\cos\alpha=$$\sqrt{\boxed{\ \ テ\ \ }}\sin\left(\alpha+\displaystyle \frac{\pi}{\boxed{\ \ ト\ \ }}\right)$
である。したがって
$\alpha=\displaystyle \frac{\boxed{\ \ ナニ\ \ }}{12}\pi, \beta=\displaystyle \frac{\boxed{\ \ ヌネ\ \ }}{12}\pi$
のとき、$s=t=0$である。
(2)次に、$s$と$t$の値を定めるときの$\theta,\alpha,\beta$の関係について考察しよう。
考察$3:s=t=0$の場合を考える。
この場合、$\sin^2\theta+\cos^2\theta=1$により、$\alpha$と$\beta$について考えると
$\cos\alpha\cos\beta+\sin\alpha\sin\beta=\displaystyle \frac{\boxed{\ \ ノハ\ \ }}{\boxed{\ \ ヒ\ \ }}$
である。
同様に、$\theta$と$\alpha$について考えると
$\cos\theta\cos\alpha+\sin\theta\sin\alpha=\displaystyle \frac{\boxed{\ \ ノハ\ \ }}{\boxed{\ \ ヒ\ \ }}$
であるから、$\theta,\alpha,\beta$の範囲に注意すると
$\beta-\alpha=\alpha-\theta=\displaystyle \frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}\pi$
という関係が得られる。
(3)これまでの考察を振り返ると、次の⓪~③のうち、
正しいものは$\boxed{\boxed{\ \ ホ\ \ }}$であることが分かる。
$\boxed{\boxed{\ \ ホ\ \ }}$の解答群
⓪$\triangle PQR$が正三角形ならば$s=t=0$であり、$s=t=0$ならば
$\triangle PQR$は正三角形である。
①$\triangle PQR$が正三角形ならば$s=t=0$であり、$s=t=0$で
あっても$\triangle PQR$は正三角形でない場合がある。
②$\triangle PQR$が正三角形であっても$s=t=0$でない場合があるが
$s=t=0$ならば$\triangle PQR$は正三角形である。
③$\triangle PQR$が正三角形であっても$s=t=0$でない場合があり、
$s=t=0$であっても$\triangle PQR$が正三角形でない場合がある。
【数Ⅱ】三角関数のグラフ③ 横の変化(y=sin(θ-π/2)、y=sin2θのグラフ)

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$y=sin(θ-π/2)、y=sin2θ$のグラフを解説していきます.
この動画を見る
$y=sin(θ-π/2)、y=sin2θ$のグラフを解説していきます.
【数Ⅱ】三角関数のグラフ② 縦の変化(y=2sinθ、y=sinθ+1のグラフ)

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角関数のグラフ①の続きです。この動画では縦の変化($y=2sinθ、y=sinθ+1$のグラフ)を扱います。
この動画を見る
三角関数のグラフ①の続きです。この動画では縦の変化($y=2sinθ、y=sinθ+1$のグラフ)を扱います。
【数Ⅱ】三角関数のグラフ①(y=sinθ、y=cosθ、y=tanθのグラフ)

共通テスト2021年数学詳しい解説〜共通テスト2021年2B第1問〜三角関数、指数関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#指数関数と対数関数#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1](1)次の問題$A$について考えよう。
$\boxed{\boxed{問題A} 関数y=\sin\theta+\sqrt3\cos\theta\left(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2}\right)$の最大値を求めよ。}$
$\sin\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{\sqrt3}{2},$ $\cos\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{1}{2}$
であるから、三角関数の合成により
$y=\boxed{\ \ イ\ \ }\sin\left(\theta+\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}\right)$
と変形できる。よって、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ ウ\ \ }}$で最大値$\ \boxed{\ \ エ\ \ }\ $をとる。
(2)$p$を定数とし、次の問題$B$について考えよう。
$\boxed{\boxed{問題B} 関数y=\sin\theta+p\cos\theta\left(0 \leqq \theta \leqq \frac{\pi}{2}\right)の最大値を求めよ。}$
$(\textrm{i})$ $p=0$のとき、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ オ\ \ }}$で最大値$\ \boxed{\ \ カ\ \ }\ $をとる。
$(\textrm{ii})$ $p \gt 0$のときは、加法定理
$\cos(\theta-\alpha)=\cos\theta\cos\alpha$$+\sin\theta\sin\alpha$
を用いると
$y=\sin\theta+p\cos\theta$$=\sqrt{\boxed{\boxed{\ \ キ\ \ }}}\cos(\theta-\alpha)$
と表すことができる。ただし、$\alpha$は
$\sin\alpha=\displaystyle \frac{\boxed{\boxed{\ \ ク\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$\cos\alpha=\frac{\boxed{\boxed{\ \ ケ\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2}$
を満たすものとする。このとき、$y$は$\theta=\boxed{\boxed{\ \ コ\ \ }}$で最大値
$\sqrt{\boxed{\boxed{\ \ サ\ \ }}}$をとる。
$(\textrm{iii})$ $p \lt 0$のとき、$y$は$\theta=\boxed{\boxed{\ \ シ\ \ }}$で最大値$\boxed{\boxed{\ \ ス\ \ }}$をとる。
$\boxed{\boxed{\ \ キ\ \ }}~\boxed{\boxed{\ \ ケ\ \ }}、\boxed{\boxed{\ \ サ\ \ }}、\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返
し選んでもよい。)
⓪$-1$
①$1$
②$-p$
③$p$
④$1-p$
⑤$1+p$
⑥$-p^2$
⑦$p^2$
⑧$1-p^2$
⑨$1+p^2$
ⓐ$(1-p)^2$
ⓑ$(1+p)^2$
$\boxed{\boxed{\ \ コ\ \ }}、\boxed{\boxed{\ \ シ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$0$
①$\alpha$
②$\displaystyle \frac{\pi}{2}$
[2]二つの関数$f(x)=\displaystyle \frac{2^x+2^{-x}}{2}$、$g(x)=\displaystyle \frac{2^x-2^{-x}}{2}$ について考える。
(1)$f(0)=\boxed{\ \ セ\ \ }、g(0)=\boxed{\ \ ソ\ \ }$である。また、$f(x)$は相加平均
と相乗平均の関係から、$x=\boxed{\ \ タ\ \ }$で最小値$\ \boxed{\ \ チ\ \ }$ をとる。
$g(x)=-2$ となる$x$の値は$\log_2\left(\sqrt{\boxed{\ \ ツ\ \ }}-\boxed{\ \ テ\ \ }\right)$である。
(3)次の①~④は、$x$にどのような値を代入しても常に成り立つ。
$f(-x)=\boxed{\boxed{\ \ ト\ \ }}$ $\cdots$①
$g(-x)=\boxed{\boxed{\ \ ナ\ \ }}$ $\cdots$②
$\left\{f(x)\right\}^2-\left\{g(x)\right\}^2=\boxed{\ \ ニ\ \ }$ $\cdots$③
$g(2x)=\boxed{\ \ ヌ\ \ }\ f(x)g(x)$ $\cdots$④
$\boxed{\boxed{\ \ ト\ \ }}、\boxed{\boxed{\ \ ナ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$f(x)$
①$-f(x)$
②$g(x)$
③$-g(x)$
(3)花子さんと太郎さんは、$f(x)$と$g(x)$の性質について話している。
花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式($\textrm{A}$)~($\textrm{D}$)を考えてみたけど、
常に成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために、式($\textrm{A}$)~($\textrm{D}$)の$\beta$に何か具体
的な値を代入して調べてみたらどうかな。
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta)$ $\cdots(\textrm{A})$
$f(\alpha+\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{B})$
$g(\alpha-\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{C})$
$g(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta)$ $\cdots(\textrm{D})$
(1),(2)で示されたことのいくつかを利用すると、式($\textrm{A}$)~($\textrm{D}$)のうち、
$\boxed{\boxed{\ \ ネ\ \ }}$以外の三つは成り立たないことが分かる。$\boxed{\boxed{\ \ ネ\ \ }}$は左辺と右辺
をそれぞれ計算することによって成り立つことが確かめられる。
$\boxed{\boxed{\ \ ネ\ \ }}$の解答群
⓪$(\textrm{A})$
①$(\textrm{B})$
②$(\textrm{C})$
③$(\textrm{D})$
2021共通テスト過去問
この動画を見る
${\large第1問}$
[1](1)次の問題$A$について考えよう。
$\boxed{\boxed{問題A} 関数y=\sin\theta+\sqrt3\cos\theta\left(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2}\right)$の最大値を求めよ。}$
$\sin\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{\sqrt3}{2},$ $\cos\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{1}{2}$
であるから、三角関数の合成により
$y=\boxed{\ \ イ\ \ }\sin\left(\theta+\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}\right)$
と変形できる。よって、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ ウ\ \ }}$で最大値$\ \boxed{\ \ エ\ \ }\ $をとる。
(2)$p$を定数とし、次の問題$B$について考えよう。
$\boxed{\boxed{問題B} 関数y=\sin\theta+p\cos\theta\left(0 \leqq \theta \leqq \frac{\pi}{2}\right)の最大値を求めよ。}$
$(\textrm{i})$ $p=0$のとき、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ オ\ \ }}$で最大値$\ \boxed{\ \ カ\ \ }\ $をとる。
$(\textrm{ii})$ $p \gt 0$のときは、加法定理
$\cos(\theta-\alpha)=\cos\theta\cos\alpha$$+\sin\theta\sin\alpha$
を用いると
$y=\sin\theta+p\cos\theta$$=\sqrt{\boxed{\boxed{\ \ キ\ \ }}}\cos(\theta-\alpha)$
と表すことができる。ただし、$\alpha$は
$\sin\alpha=\displaystyle \frac{\boxed{\boxed{\ \ ク\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$\cos\alpha=\frac{\boxed{\boxed{\ \ ケ\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2}$
を満たすものとする。このとき、$y$は$\theta=\boxed{\boxed{\ \ コ\ \ }}$で最大値
$\sqrt{\boxed{\boxed{\ \ サ\ \ }}}$をとる。
$(\textrm{iii})$ $p \lt 0$のとき、$y$は$\theta=\boxed{\boxed{\ \ シ\ \ }}$で最大値$\boxed{\boxed{\ \ ス\ \ }}$をとる。
$\boxed{\boxed{\ \ キ\ \ }}~\boxed{\boxed{\ \ ケ\ \ }}、\boxed{\boxed{\ \ サ\ \ }}、\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返
し選んでもよい。)
⓪$-1$
①$1$
②$-p$
③$p$
④$1-p$
⑤$1+p$
⑥$-p^2$
⑦$p^2$
⑧$1-p^2$
⑨$1+p^2$
ⓐ$(1-p)^2$
ⓑ$(1+p)^2$
$\boxed{\boxed{\ \ コ\ \ }}、\boxed{\boxed{\ \ シ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$0$
①$\alpha$
②$\displaystyle \frac{\pi}{2}$
[2]二つの関数$f(x)=\displaystyle \frac{2^x+2^{-x}}{2}$、$g(x)=\displaystyle \frac{2^x-2^{-x}}{2}$ について考える。
(1)$f(0)=\boxed{\ \ セ\ \ }、g(0)=\boxed{\ \ ソ\ \ }$である。また、$f(x)$は相加平均
と相乗平均の関係から、$x=\boxed{\ \ タ\ \ }$で最小値$\ \boxed{\ \ チ\ \ }$ をとる。
$g(x)=-2$ となる$x$の値は$\log_2\left(\sqrt{\boxed{\ \ ツ\ \ }}-\boxed{\ \ テ\ \ }\right)$である。
(3)次の①~④は、$x$にどのような値を代入しても常に成り立つ。
$f(-x)=\boxed{\boxed{\ \ ト\ \ }}$ $\cdots$①
$g(-x)=\boxed{\boxed{\ \ ナ\ \ }}$ $\cdots$②
$\left\{f(x)\right\}^2-\left\{g(x)\right\}^2=\boxed{\ \ ニ\ \ }$ $\cdots$③
$g(2x)=\boxed{\ \ ヌ\ \ }\ f(x)g(x)$ $\cdots$④
$\boxed{\boxed{\ \ ト\ \ }}、\boxed{\boxed{\ \ ナ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$f(x)$
①$-f(x)$
②$g(x)$
③$-g(x)$
(3)花子さんと太郎さんは、$f(x)$と$g(x)$の性質について話している。
花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式($\textrm{A}$)~($\textrm{D}$)を考えてみたけど、
常に成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために、式($\textrm{A}$)~($\textrm{D}$)の$\beta$に何か具体
的な値を代入して調べてみたらどうかな。
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta)$ $\cdots(\textrm{A})$
$f(\alpha+\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{B})$
$g(\alpha-\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{C})$
$g(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta)$ $\cdots(\textrm{D})$
(1),(2)で示されたことのいくつかを利用すると、式($\textrm{A}$)~($\textrm{D}$)のうち、
$\boxed{\boxed{\ \ ネ\ \ }}$以外の三つは成り立たないことが分かる。$\boxed{\boxed{\ \ ネ\ \ }}$は左辺と右辺
をそれぞれ計算することによって成り立つことが確かめられる。
$\boxed{\boxed{\ \ ネ\ \ }}$の解答群
⓪$(\textrm{A})$
①$(\textrm{B})$
②$(\textrm{C})$
③$(\textrm{D})$
2021共通テスト過去問
【数Ⅱ】三角関数:弧度法の考え方② -19π/6って第何象限でどんな形?!

【数Ⅱ】三角関数:弧度法の考え方①

14京都府教員採用試験(数学:5番 三角関数)

単元:
#数Ⅱ#三角関数#三角関数とグラフ#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
5⃣$y=a(1+sinx)cosx(0 \leqq x \leqq 2\pi)$
の最大値が18のときaの値を求めよ。(a>0)
この動画を見る
5⃣$y=a(1+sinx)cosx(0 \leqq x \leqq 2\pi)$
の最大値が18のときaの値を求めよ。(a>0)
【数学Ⅱ】三角関数の式の証明

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学Ⅱ】三角関数の式の証明解説動画です
-----------------
$\displaystyle \frac{cos^2 \theta - \sin^2 \theta}{1+2 \sin \theta \cos \theta}=\displaystyle \frac{1- \tan \theta}{1+ \tan \theta}$
この動画を見る
【数学Ⅱ】三角関数の式の証明解説動画です
-----------------
$\displaystyle \frac{cos^2 \theta - \sin^2 \theta}{1+2 \sin \theta \cos \theta}=\displaystyle \frac{1- \tan \theta}{1+ \tan \theta}$
19奈良県教員採用試験(数学:2番 三角関数)

単元:
#数Ⅱ#三角関数#三角関数とグラフ#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣$0 \leqq θ \leqq \pi$
$y= sin2θ + 2(sinθ+cosθ)-i$のMAX、minとそのときのθの値を求めよ。
この動画を見る
2⃣$0 \leqq θ \leqq \pi$
$y= sin2θ + 2(sinθ+cosθ)-i$のMAX、minとそのときのθの値を求めよ。
京都大学 5倍角の公式

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#数Ⅱ#三角関数#三角関数とグラフ
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\cos5\theta=f(\cos\theta)$を満たす多項式$f(n)$を求めよ.
(2)$\cos\dfrac{\pi}{10}\cos\dfrac{3\pi}{10}\cos\dfrac{7\pi}{10}\cos\dfrac{9\pi}{10}=\dfrac{5}{16}$を示せ.
1996京都大過去問
この動画を見る
(1)$\cos5\theta=f(\cos\theta)$を満たす多項式$f(n)$を求めよ.
(2)$\cos\dfrac{\pi}{10}\cos\dfrac{3\pi}{10}\cos\dfrac{7\pi}{10}\cos\dfrac{9\pi}{10}=\dfrac{5}{16}$を示せ.
1996京都大過去問
【コツ】三角関数のグラフの書き方

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
三角関数のグラフの書き方紹介動画です
-----------------
(1)$y=\sin(\theta -\displaystyle \frac{\pi}{3})$
(2)$y=\cos(\theta+\displaystyle \frac{\pi}{6})$
(3)$y=\tan(\theta-\displaystyle \frac{\pi}{4})$
この動画を見る
三角関数のグラフの書き方紹介動画です
-----------------
(1)$y=\sin(\theta -\displaystyle \frac{\pi}{3})$
(2)$y=\cos(\theta+\displaystyle \frac{\pi}{6})$
(3)$y=\tan(\theta-\displaystyle \frac{\pi}{4})$
