 三角関数
三角関数
 三角関数
三角関数
福田の数学〜2023年共通テスト速報〜数学IIB第1問三角関数と対数〜三角不等式と対数が有理数とならない条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
この動画を見る
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
大学入試問題#420【イントロ・エンディング変えてみた】「三角比の基本的な計算」 藤田保健衛生大学医学部2014 #三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \alpha,\ \beta \leqq \pi$
$\begin{eqnarray}
\left\{
\begin{array}{l}
1-\cos\alpha+(\alpha+\beta)=0 \\
1-\cos\beta+\cos(\alpha+\beta)=0
\end{array}
\right.
\end{eqnarray}$
を満たす組$(\alpha,\beta)$を全て求めよ
この動画を見る
$0 \leqq \alpha,\ \beta \leqq \pi$
$\begin{eqnarray}
\left\{
\begin{array}{l}
1-\cos\alpha+(\alpha+\beta)=0 \\
1-\cos\beta+\cos(\alpha+\beta)=0
\end{array}
\right.
\end{eqnarray}$
を満たす組$(\alpha,\beta)$を全て求めよ
東京電機大 最大値・最小値

単元:
#数Ⅰ#数Ⅱ#2次関数#2次関数とグラフ#三角関数#三角関数とグラフ#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yを実数とする.
$x^2+2y^2+4y=0$を満たすとき,$2x-y$の最大値・最小値を求めよ.
東京電機大過去問
この動画を見る
x,yを実数とする.
$x^2+2y^2+4y=0$を満たすとき,$2x-y$の最大値・最小値を求めよ.
東京電機大過去問
福田の1.5倍速演習〜合格する重要問題048〜早稲田大学2019年度商学部第1問(1)〜2変数の三角関数の最大最小問題

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)$\alpha,\beta$を実数とする。
$2\cos\alpha\sin\beta+3\sin\alpha\sin\beta+4\cos\beta$
の最小値は$\boxed{ア}$である。
2019早稲田大学商学部過去問
この動画を見る
(1)$\alpha,\beta$を実数とする。
$2\cos\alpha\sin\beta+3\sin\alpha\sin\beta+4\cos\beta$
の最小値は$\boxed{ア}$である。
2019早稲田大学商学部過去問
π<3 .3 示せ(類)浜松医科大学2022

福田の1.5倍速演習〜合格する重要問題038〜京都大学2017年度理系第3問〜三角関数と自然数解

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#三角関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$p,q$を自然数,$\alpha,\beta$を
$\tan\alpha=\frac{1}{p}$,$\tan\beta=\frac{1}{q}$
を満たす実数とする。このとき、
$\tan(\alpha+2\beta)=2$
を満たすp,qの組(p,q)を全て求めよ。
2017京都大学理系過去問
この動画を見る
$p,q$を自然数,$\alpha,\beta$を
$\tan\alpha=\frac{1}{p}$,$\tan\beta=\frac{1}{q}$
を満たす実数とする。このとき、
$\tan(\alpha+2\beta)=2$
を満たすp,qの組(p,q)を全て求めよ。
2017京都大学理系過去問
【高校数学】和積の公式・積和の公式~覚えず導こう~【数学Ⅱ】

福田の1.5倍速演習〜合格する重要問題029〜九州大学2016年度理系第5問〜ドモアブルの定理と三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#三角関数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)$\theta$を$0 \leqq \theta \lt 2\pi$を満たす実数、iを虚数単位とし、$z=\cos\theta+i\sin\theta$で
表される複素数とする。このとき、整数nに対して次の式を証明せよ。
$\cos n\theta=\frac{1}{2}\left(z^n+\frac{1}{z^n}\right), \sin n\theta=-\frac{i}{2}\left(z^n-\frac{1}{z^n}\right)$
(2)次の方程式を満たす実数$x(0 \leqq x \lt 2\pi)$を求めよ。
$\cos x+\cos2x-\cos3x=1$
(3)次の式を証明せよ。
$\sin^220°+\sin^240°+\sin^260°+\sin^280°=\frac{9}{4}$
2016九州大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)$\theta$を$0 \leqq \theta \lt 2\pi$を満たす実数、iを虚数単位とし、$z=\cos\theta+i\sin\theta$で
表される複素数とする。このとき、整数nに対して次の式を証明せよ。
$\cos n\theta=\frac{1}{2}\left(z^n+\frac{1}{z^n}\right), \sin n\theta=-\frac{i}{2}\left(z^n-\frac{1}{z^n}\right)$
(2)次の方程式を満たす実数$x(0 \leqq x \lt 2\pi)$を求めよ。
$\cos x+\cos2x-\cos3x=1$
(3)次の式を証明せよ。
$\sin^220°+\sin^240°+\sin^260°+\sin^280°=\frac{9}{4}$
2016九州大学理系過去問
福田の数学〜北里大学2021年医学部第1問(3)〜三角関数への置き換えによる最大値の求め方

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)$0 \leqq \theta \lt 2\pi$のとき、関数$f(\theta)=2\cos\theta(\sqrt3\sin\theta+\cos\theta)$の最大値は
$\boxed{ ケ}$である。
$g(x,y)=\frac{2\sqrt3xy+2x^2}{x^4+2x^2y^2+y^4+1}$について考える。aを正の定数とし、点(x,y)が
円$x^2+y^2=a^2$上を動くとき、g$(x,y)$の最大値はaを用いて$\boxed{コ}$と表せる。
また、点(x,y)がxy平面全体を動くとき、g(x,y)の最大値は$\boxed{サ}$である。
2021北里大学医学部過去問
この動画を見る
(3)$0 \leqq \theta \lt 2\pi$のとき、関数$f(\theta)=2\cos\theta(\sqrt3\sin\theta+\cos\theta)$の最大値は
$\boxed{ ケ}$である。
$g(x,y)=\frac{2\sqrt3xy+2x^2}{x^4+2x^2y^2+y^4+1}$について考える。aを正の定数とし、点(x,y)が
円$x^2+y^2=a^2$上を動くとき、g$(x,y)$の最大値はaを用いて$\boxed{コ}$と表せる。
また、点(x,y)がxy平面全体を動くとき、g(x,y)の最大値は$\boxed{サ}$である。
2021北里大学医学部過去問
東大医学部ベテランちが5浪TAWASHIに早稲田の数学の問題を解説

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
東大医学部のベテランちさんが、TAWASHIさんに早稲田大学の数学入試を解説します。
問題の解き方を理解しましょう!
この動画を見る
東大医学部のベテランちさんが、TAWASHIさんに早稲田大学の数学入試を解説します。
問題の解き方を理解しましょう!
福田の1.5倍速演習〜合格する重要問題007〜大阪大学2015年文系数学第1問〜不等式の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#三角関数#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数x,yが$|x| \leqq 1$と$|y| \leqq 1$を満たすとき、不等式
$0 \leqq x^2+y^2-2x^2y^2+2xy\sqrt{1-x^2}\sqrt{1-y^2} \leqq 1$
が成り立つことを示せ。
2015大阪大学文系過去問
この動画を見る
実数x,yが$|x| \leqq 1$と$|y| \leqq 1$を満たすとき、不等式
$0 \leqq x^2+y^2-2x^2y^2+2xy\sqrt{1-x^2}\sqrt{1-y^2} \leqq 1$
が成り立つことを示せ。
2015大阪大学文系過去問
福田の数学〜東京理科大学2022年理工学部第1問(2)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)角θに関する方程式
$\cos 4θ=\cos θ(0\leqq θ\leqq \pi)$
について考える。①を満たすθは小さい方から順に
$θ=0,\frac{\boxed{キ}}{\boxed{ク}}\pi,\frac{\boxed{ケ}}{\boxed{コ}}\pi,\frac{\boxed{サ}}{\boxed{シ}}\pi$
の4つである。一方、θが①を満たすとき、$t=\cos θ$とおくとtは
$\boxed{ス}t^4 - \boxed{セ}t^2+\boxed{ソ}=t$
を満たす。$t=1,\cos \frac{\boxed{ケ}}{\boxed{コ}}\pi$は②の解なので、2次方程式
$\boxed{タ}t^2+\boxed{チ}t-1=0$
は$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi,\cos \frac{\boxed{サ}}{\boxed{シ}}\pi$を解にもつ。これより、
$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi=\frac{\sqrt{\boxed{ツ}}-\boxed{テ}}{\boxed{ト}},\cos \frac{\boxed{サ}}{\boxed{シ}}\pi=-\frac{\sqrt{\boxed{ツ}}+\boxed{テ}}{\boxed{ト}}$であることが分かる。
この動画を見る
(2)角θに関する方程式
$\cos 4θ=\cos θ(0\leqq θ\leqq \pi)$
について考える。①を満たすθは小さい方から順に
$θ=0,\frac{\boxed{キ}}{\boxed{ク}}\pi,\frac{\boxed{ケ}}{\boxed{コ}}\pi,\frac{\boxed{サ}}{\boxed{シ}}\pi$
の4つである。一方、θが①を満たすとき、$t=\cos θ$とおくとtは
$\boxed{ス}t^4 - \boxed{セ}t^2+\boxed{ソ}=t$
を満たす。$t=1,\cos \frac{\boxed{ケ}}{\boxed{コ}}\pi$は②の解なので、2次方程式
$\boxed{タ}t^2+\boxed{チ}t-1=0$
は$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi,\cos \frac{\boxed{サ}}{\boxed{シ}}\pi$を解にもつ。これより、
$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi=\frac{\sqrt{\boxed{ツ}}-\boxed{テ}}{\boxed{ト}},\cos \frac{\boxed{サ}}{\boxed{シ}}\pi=-\frac{\sqrt{\boxed{ツ}}+\boxed{テ}}{\boxed{ト}}$であることが分かる。
福田の数学〜中央大学2022年経済学部第1問(3)〜三角不等式

単元:
#大学入試過去問(数学)#三角関数#加法定理とその応用#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(3)$0\leqq x\leqq \pi$のとき、次の不等式を解け。
$\sin^2x-\cos^2x+sinx \gt 0$
2022中央大学経済学部過去問
この動画を見る
(3)$0\leqq x\leqq \pi$のとき、次の不等式を解け。
$\sin^2x-\cos^2x+sinx \gt 0$
2022中央大学経済学部過去問
福田の数学〜杏林大学2022年医学部第1問〜三角関数の最大最小と極値

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#加法定理とその応用#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学
指導講師:
福田次郎
問題文全文(内容文):
(1)三角関数について、次の等式が成り立つ。
$\cos2θ=\boxed{アイ}\sin^2θ+\boxed{ウ}$
$\sin3θ=\boxed{エオ}\sin^3θ+\boxed{カ}\sinθ$
(2)$0 \leqq θ \lt 2\pi$のとき、関数
$y=-\frac{1}{12}\sin3θ+\frac{3}{8}\cos2θ-\frac{3}{4}\sinθ$
は$θ=\frac{\boxed{キ}}{\boxed{ク}}\pi$で最小値$\frac{\boxed{ケコサ}}{\boxed{シス}}$をとり、
$\sinθ=\frac{\boxed{セソ}}{\boxed{タ}}$のとき最大値$\frac{\boxed{チツ}}{\boxed{テト}}$
をとる。また、yの極致を与えるθの個数は$\boxed{ナ}$である。
2022杏林大学医学部過去問
この動画を見る
(1)三角関数について、次の等式が成り立つ。
$\cos2θ=\boxed{アイ}\sin^2θ+\boxed{ウ}$
$\sin3θ=\boxed{エオ}\sin^3θ+\boxed{カ}\sinθ$
(2)$0 \leqq θ \lt 2\pi$のとき、関数
$y=-\frac{1}{12}\sin3θ+\frac{3}{8}\cos2θ-\frac{3}{4}\sinθ$
は$θ=\frac{\boxed{キ}}{\boxed{ク}}\pi$で最小値$\frac{\boxed{ケコサ}}{\boxed{シス}}$をとり、
$\sinθ=\frac{\boxed{セソ}}{\boxed{タ}}$のとき最大値$\frac{\boxed{チツ}}{\boxed{テト}}$
をとる。また、yの極致を与えるθの個数は$\boxed{ナ}$である。
2022杏林大学医学部過去問
難問です!三角関数と整数の融合問題!解けますか?【一橋大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形$ABC$において,$ tanA,tanB,tanC$の値がすべて整数であるとき,それらの値を求めよ。
一橋大過去問
この動画を見る
三角形$ABC$において,$ tanA,tanB,tanC$の値がすべて整数であるとき,それらの値を求めよ。
一橋大過去問
三角関数の基礎問題です!2通りで解説【一橋大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形$ABC$において,$\angle A=60°$であるとする。
(1)$sinB+sinC$の取り得る値の範囲を求めよ。
(2)$sinBsinC$の取り得る値の範囲を求めよ。
一橋大過去問
この動画を見る
三角形$ABC$において,$\angle A=60°$であるとする。
(1)$sinB+sinC$の取り得る値の範囲を求めよ。
(2)$sinBsinC$の取り得る値の範囲を求めよ。
一橋大過去問
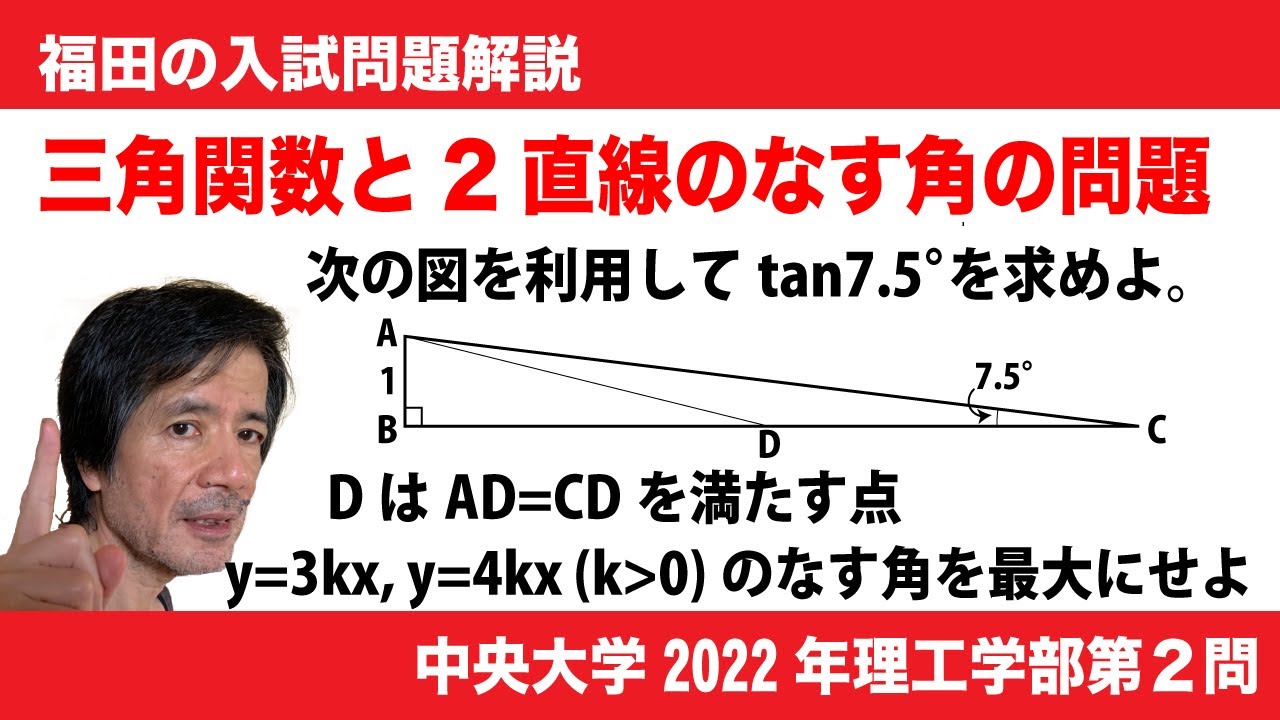
福田の数学〜中央大学2022年理工学部第2問〜三角関数と2直線のなす角
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$AB = 1, \angle ABC = 90°,\angle BCA = 7.5°$である$△ABC$ の辺BC 上に $AD = CD$ と
なるように点Dをとる。このとき、$BD = \boxed{コ}, CD=\boxed{サ}$である。したがって、
$\tan 7.5° =\frac{1}{\boxed{コ}+\boxed{サ}}$
次に、正の実数kに対して、2直線$y=3kx, y = 4kx$のなす角度を$θ$とする。
だし、$0° \lt θ \lt 90°$である。このとき、$\tanθ = \boxed{シ}$である。したがって、$\tanθ$ は
$k =\frac{1}{\boxed{ス}}$ のとき最大値$\frac{1}{\boxed{セ}}$ をとる。また、$k=\frac{1}{\boxed{ス}}$ のとき$\boxed{ソ}$を満たす。
なお、必要ならば
$\sqrt2 = 1.4, \sqrt3=1.7..., \sqrt5=2.2, \sqrt6=2.4...$
を用いてよい。
$\boxed{コ},\boxed{サ}$の解答群
$ⓐ\sqrt2+\sqrt3\ \ \ ⓑ\sqrt2+\sqrt5\ \ \ ⓒ\sqrt2+\sqrt6\ \ \ ⓓ2+\sqrt3$
$ⓔ2+\sqrt5\ \ \ ⓕ2+\sqrt6\ \ \ ⓖ\sqrt3+\sqrt5\ \ \ ⓗ\sqrt5+\sqrt6$
$\boxed{シ}$の解答群
$ⓐ\frac{k}{1-12k^2}\ \ \ ⓑ\frac{k}{1+12k^2}\ \ \ ⓒ\frac{7k}{1-12k^2}\ \ \ ⓓ\frac{7k}{1+12k^2}$
$ⓔ\frac{12k^2}{1-12k^2}\ \ \ ⓕ\frac{12k^2}{1+12k^2}$
$ⓖ\frac{12k^2}{1-7k^2}\ \ \ ⓗ\frac{12k^2}{1+7k^2}$
$\boxed{ス},\boxed{セ}$の解答群
$ⓐ2\ \ \ ⓑ2\sqrt2\ \ \ ⓒ3\ \ \ ⓓ2\sqrt3\ \ \ ⓔ4\ \ \ ⓕ3\sqrt2$
$ⓖ3\sqrt3 \ \ \ ⓗ4\sqrt2 \ \ \ ⓘ6\ \ \ ⓙ4\sqrt3 \ \ \ ⓚ7\ \ \ ⓛ7\sqrt2$
$\boxed{ソ}$の解答群
$ⓐθ \gt 7.5°\ \ \ ⓑθ = 7.5°\ \ \ ⓒθ \lt 7.5°$
2022中央大学理工学部過去問
この動画を見る
$AB = 1, \angle ABC = 90°,\angle BCA = 7.5°$である$△ABC$ の辺BC 上に $AD = CD$ と
なるように点Dをとる。このとき、$BD = \boxed{コ}, CD=\boxed{サ}$である。したがって、
$\tan 7.5° =\frac{1}{\boxed{コ}+\boxed{サ}}$
次に、正の実数kに対して、2直線$y=3kx, y = 4kx$のなす角度を$θ$とする。
だし、$0° \lt θ \lt 90°$である。このとき、$\tanθ = \boxed{シ}$である。したがって、$\tanθ$ は
$k =\frac{1}{\boxed{ス}}$ のとき最大値$\frac{1}{\boxed{セ}}$ をとる。また、$k=\frac{1}{\boxed{ス}}$ のとき$\boxed{ソ}$を満たす。
なお、必要ならば
$\sqrt2 = 1.4, \sqrt3=1.7..., \sqrt5=2.2, \sqrt6=2.4...$
を用いてよい。
$\boxed{コ},\boxed{サ}$の解答群
$ⓐ\sqrt2+\sqrt3\ \ \ ⓑ\sqrt2+\sqrt5\ \ \ ⓒ\sqrt2+\sqrt6\ \ \ ⓓ2+\sqrt3$
$ⓔ2+\sqrt5\ \ \ ⓕ2+\sqrt6\ \ \ ⓖ\sqrt3+\sqrt5\ \ \ ⓗ\sqrt5+\sqrt6$
$\boxed{シ}$の解答群
$ⓐ\frac{k}{1-12k^2}\ \ \ ⓑ\frac{k}{1+12k^2}\ \ \ ⓒ\frac{7k}{1-12k^2}\ \ \ ⓓ\frac{7k}{1+12k^2}$
$ⓔ\frac{12k^2}{1-12k^2}\ \ \ ⓕ\frac{12k^2}{1+12k^2}$
$ⓖ\frac{12k^2}{1-7k^2}\ \ \ ⓗ\frac{12k^2}{1+7k^2}$
$\boxed{ス},\boxed{セ}$の解答群
$ⓐ2\ \ \ ⓑ2\sqrt2\ \ \ ⓒ3\ \ \ ⓓ2\sqrt3\ \ \ ⓔ4\ \ \ ⓕ3\sqrt2$
$ⓖ3\sqrt3 \ \ \ ⓗ4\sqrt2 \ \ \ ⓘ6\ \ \ ⓙ4\sqrt3 \ \ \ ⓚ7\ \ \ ⓛ7\sqrt2$
$\boxed{ソ}$の解答群
$ⓐθ \gt 7.5°\ \ \ ⓑθ = 7.5°\ \ \ ⓒθ \lt 7.5°$
2022中央大学理工学部過去問
【分ければカンタン!】三角関数のグラフの移動と拡大を5分で解説!〔数学、高校数学〕

【解答にミスあり概要欄】大学入試問題#322 慶應義塾大学(2021) #三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$-\displaystyle \frac{\pi}{2} \leqq \theta \leqq \displaystyle \frac{\pi}{2}$
$4\cos\displaystyle \frac{\theta}{2}(\cos\displaystyle \frac{\theta}{2}+\sin\displaystyle \frac{\theta}{2})$のとき
$\sin\theta$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$-\displaystyle \frac{\pi}{2} \leqq \theta \leqq \displaystyle \frac{\pi}{2}$
$4\cos\displaystyle \frac{\theta}{2}(\cos\displaystyle \frac{\theta}{2}+\sin\displaystyle \frac{\theta}{2})$のとき
$\sin\theta$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
福田の数学〜立教大学2022年理学部第1問(2)〜余事象と確率の加法定理

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
下図のように1から9までの数字が1つずつ記入された、9枚のカードがある。
$\boxed{1}\ \ \ \boxed{2}\ \ \ \boxed{3}\ \ \ \boxed{4}\ \ \ \boxed{5}\ \ \ \boxed{6}\ \ \ \boxed{7}\ \ \ \boxed{8}\ \ \ \boxed{9}$
これら9枚のカードから同時に取り出した3枚のカードの数字の積が
10で割り切れる確率は$\boxed{イ}$である。
2022立教大学理学部過去問
この動画を見る
下図のように1から9までの数字が1つずつ記入された、9枚のカードがある。
$\boxed{1}\ \ \ \boxed{2}\ \ \ \boxed{3}\ \ \ \boxed{4}\ \ \ \boxed{5}\ \ \ \boxed{6}\ \ \ \boxed{7}\ \ \ \boxed{8}\ \ \ \boxed{9}$
これら9枚のカードから同時に取り出した3枚のカードの数字の積が
10で割り切れる確率は$\boxed{イ}$である。
2022立教大学理学部過去問
【数Ⅱ】三角関数:3倍角の公式笑っちゃう覚え方

福田の数学〜明治大学2022年理工学部第2問〜平面図形の計量

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#英語(高校生)#平面図形#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#明治大学#数学(高校生)#明治大学
指導講師:
福田次郎
問題文全文(内容文):
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
この動画を見る
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
【数学II】三角関数_これで共テ瞬殺!【三角関数のイメージ】【共通テスト】

単元:
#三角関数#三角関数とグラフ#加法定理とその応用#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
(1)
$0^{ \circ } \lt \theta \lt 180^{ \circ }$
$\tan \theta =-2$
$\sin \theta,\cos \theta$は?
(2)
$0 \leqq \theta \lt 2 \pi$
$\cos \theta \lt \displaystyle \frac{\sqrt{ 3 }}{2}$を解け
(3)
$0 \lt \theta \leqq 2 \pi$
$\sin \theta \geqq \displaystyle \frac{1}{2}$を解け
(4)
$0 \leqq \theta \lt 2 \pi$
$\sin \theta + \sqrt{ 3 } \cos \theta =\sqrt{ 2 }$を解け
(5)
$0 \leqq x \leqq \pi$とする
$y=2 \sin 2x-2(\sin x- \cos x)+1$
のとり得る値の範囲は?
(6)
$f(x)=\sin x - \cos 2x$の
$0 \leqq x \leqq \pi$における
max、minを求めよ
この動画を見る
(1)
$0^{ \circ } \lt \theta \lt 180^{ \circ }$
$\tan \theta =-2$
$\sin \theta,\cos \theta$は?
(2)
$0 \leqq \theta \lt 2 \pi$
$\cos \theta \lt \displaystyle \frac{\sqrt{ 3 }}{2}$を解け
(3)
$0 \lt \theta \leqq 2 \pi$
$\sin \theta \geqq \displaystyle \frac{1}{2}$を解け
(4)
$0 \leqq \theta \lt 2 \pi$
$\sin \theta + \sqrt{ 3 } \cos \theta =\sqrt{ 2 }$を解け
(5)
$0 \leqq x \leqq \pi$とする
$y=2 \sin 2x-2(\sin x- \cos x)+1$
のとり得る値の範囲は?
(6)
$f(x)=\sin x - \cos 2x$の
$0 \leqq x \leqq \pi$における
max、minを求めよ
福田の数学〜早稲田大学2022年商学部第3問〜空間図形の計量

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
この動画を見る
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
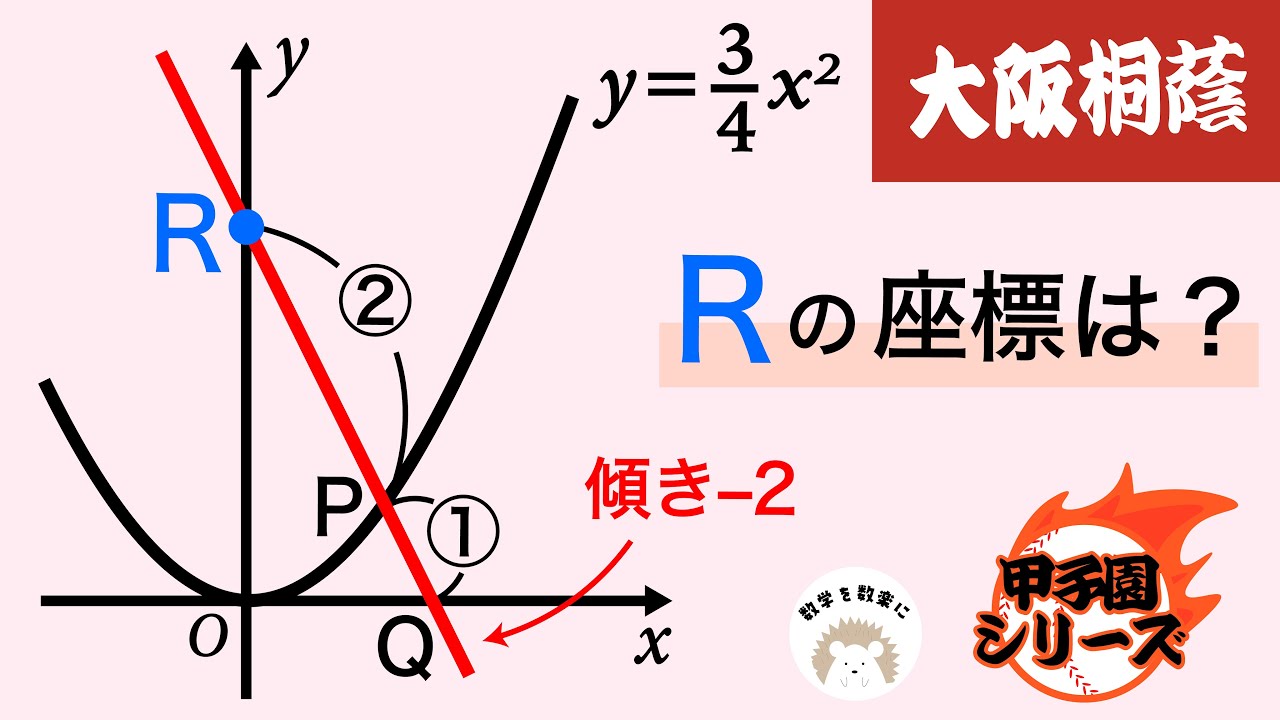
放物線と比 大阪桐蔭
単元:
#数学(中学生)#数Ⅰ#数Ⅱ#2次関数#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
Rの座標は?
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
Rの座標は?
*図は動画内参照
大阪桐蔭高等学校
これ知ってる?ある公式を知ってれば一瞬で解ける問題! #Shorts

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ tan30°=tan 10°・tan50°・tan70°$を示せ。
この動画を見る
$ tan30°=tan 10°・tan50°・tan70°$を示せ。
3通りで証明できる!?おもしろい解法を紹介【数学 三角関数】

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$tan10°=tan20°・tan30°・tan40°$を示せ。
この動画を見る
$tan10°=tan20°・tan30°・tan40°$を示せ。
福田の数学〜早稲田大学2022年人間科学部第2問〜三角不等式の解

単元:
#大学入試過去問(数学)#三角関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}2\sin\theta+\sin2\theta+2\sin3\theta-2\sin2\theta\cos\theta \gt 0\hspace{10pt}(0 \lt \theta \lt \pi)$
を満たす$\theta$の範囲は
$0 \lt \theta \lt \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\ \pi,\ \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\ \pi \lt \theta \lt \pi$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{2}}2\sin\theta+\sin2\theta+2\sin3\theta-2\sin2\theta\cos\theta \gt 0\hspace{10pt}(0 \lt \theta \lt \pi)$
を満たす$\theta$の範囲は
$0 \lt \theta \lt \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\ \pi,\ \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\ \pi \lt \theta \lt \pi$
である。
2022早稲田大学人間科学部過去問
福田の数学〜早稲田大学2022年人間科学部第1問(3)〜三角形の辺の関係から角の関係を求める

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#三角関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)$\triangle ABC$において、3つの角の大きさをA,B,Cとし、
それぞれの対辺の長さをa,b,cとする。
$5a^2-5b^2+6bc-5c^2=0$
のとき、$\sin2A+\cos2A=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(3)$\triangle ABC$において、3つの角の大きさをA,B,Cとし、
それぞれの対辺の長さをa,b,cとする。
$5a^2-5b^2+6bc-5c^2=0$
のとき、$\sin2A+\cos2A=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。
2022早稲田大学人間科学部過去問
福田の数学〜慶應義塾大学2022年看護医療学部第1問(3)〜三角関数の最大最小の種類

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)関数$f(\theta)=\cos2\theta+2\cos\theta$が
$0 \leqq \theta \leqq \pi$ の範囲で最小値をとるのは$\theta=\boxed{\ \ ア\ \ }$
のときであり、最大値を取るのは$\theta=\boxed{\ \ イ\ \ }$のときである。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(3)関数$f(\theta)=\cos2\theta+2\cos\theta$が
$0 \leqq \theta \leqq \pi$ の範囲で最小値をとるのは$\theta=\boxed{\ \ ア\ \ }$
のときであり、最大値を取るのは$\theta=\boxed{\ \ イ\ \ }$のときである。
2022慶應義塾大学看護医療学科過去問
