 三角関数
三角関数
 三角関数
三角関数
福田のわかった数学〜高校2年生063〜三角関数(2)三角関数の定義

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 三角関数(2) 三角関数の定義
一般角$\theta$に対して
$\sin\theta, \cos\theta$
の定義を説明せよ。
この動画を見る
数学$\textrm{II}$ 三角関数(2) 三角関数の定義
一般角$\theta$に対して
$\sin\theta, \cos\theta$
の定義を説明せよ。
福田のわかった数学〜高校3年生理系080〜グラフを描こう(2)三角関数のグラフ

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(2)
$y=\cos2x-2\cos x (0 \leqq x \leqq 2\pi)$
のグラフを描け。ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(2)
$y=\cos2x-2\cos x (0 \leqq x \leqq 2\pi)$
のグラフを描け。ただし凹凸は調べなくてよい。
福田のわかった数学〜高校2年生062〜三角関数(1)三角関数のグラフ
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
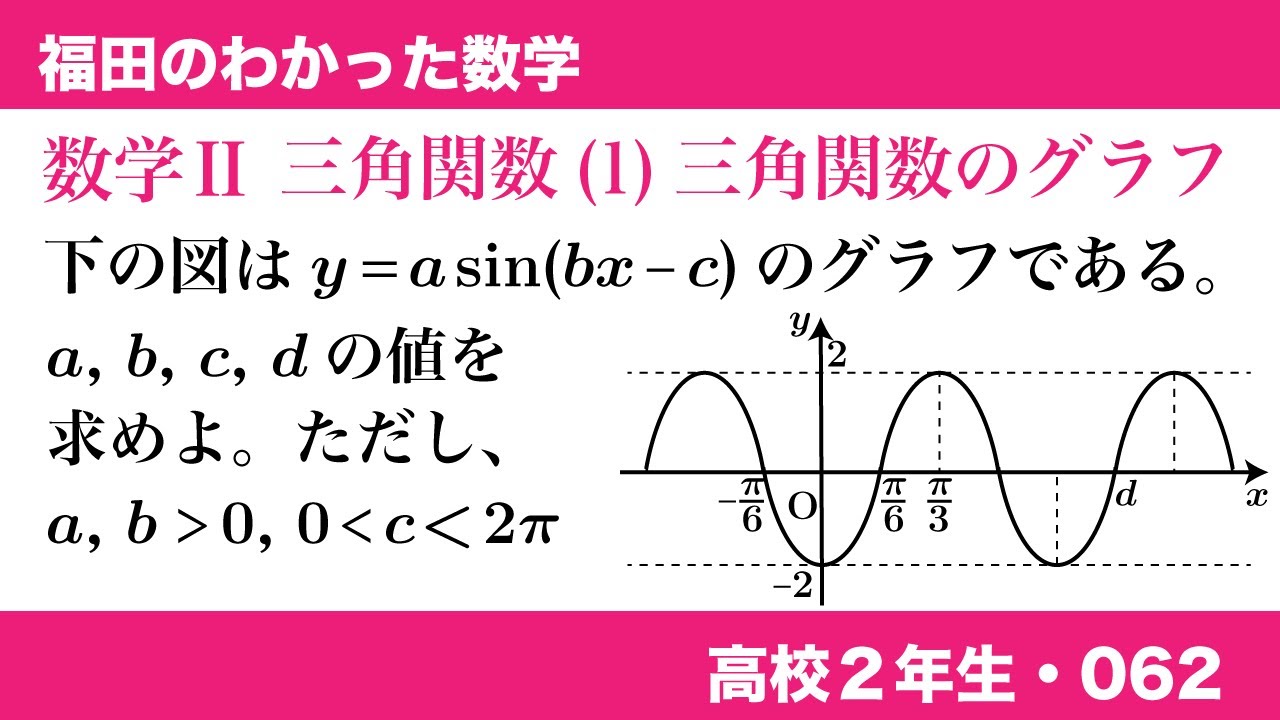
数学$\textrm{II}$ 三角関数(1) 三角関数のグラフ
下の図は$y=a\sin(bx-c)$のグラフである。
$a,b,c,d$の値を求めよ。ただし、$a \gt 0,\ b \gt 0,\ 0 \lt c \lt 2\pi$
とする。(※図は動画参照)
この動画を見る
数学$\textrm{II}$ 三角関数(1) 三角関数のグラフ
下の図は$y=a\sin(bx-c)$のグラフである。
$a,b,c,d$の値を求めよ。ただし、$a \gt 0,\ b \gt 0,\ 0 \lt c \lt 2\pi$
とする。(※図は動画参照)
【高校数学】3倍角の公式~簡単に導出できます~ 4-13.5【数学Ⅱ】

福田の数学〜明治大学2021年理工学部第1問(2)〜三角関数の最大最小

単元:
#数Ⅱ#三角関数#三角関数とグラフ#加法定理とその応用#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)座標平面上に2点$A(\frac{5}{8},0),\ B(0,\frac{3}{2})$をとる。Lは原点を通る直線で、Lが
x軸の正の方向となす角$\thetaは0 \leqq \theta \leqq \frac{\pi}{2}$の範囲にあるとする。ただし、角$\theta$の
符号は時計の針の回転と逆の向きを正の方向とする。点Aと直線Lとの距離を
$d_A$、点Bと直線Lの距離を$d_B$とおく。このとき、
$d_A+d_B=\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}\sin\theta+\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\cos\theta$
である。$\theta$が$0 \leqq \theta \leqq \frac{\pi}{2}$の範囲を動くとき、
$d_A+d_B$の最大値は$\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
最小値は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(2)座標平面上に2点$A(\frac{5}{8},0),\ B(0,\frac{3}{2})$をとる。Lは原点を通る直線で、Lが
x軸の正の方向となす角$\thetaは0 \leqq \theta \leqq \frac{\pi}{2}$の範囲にあるとする。ただし、角$\theta$の
符号は時計の針の回転と逆の向きを正の方向とする。点Aと直線Lとの距離を
$d_A$、点Bと直線Lの距離を$d_B$とおく。このとき、
$d_A+d_B=\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}\sin\theta+\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\cos\theta$
である。$\theta$が$0 \leqq \theta \leqq \frac{\pi}{2}$の範囲を動くとき、
$d_A+d_B$の最大値は$\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
最小値は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。
2021明治大学理工学部過去問
福田のわかった数学〜高校1年生061〜三角形の形状決定問題(2)

単元:
#数Ⅰ#数Ⅱ#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形の形状決定(2)
次の等式が成り立つとき、$\triangle ABC$はどんな形の三角形か。
$\sin A\cos A=\sin B\cos B$
この動画を見る
数学$\textrm{I}$ 三角形の形状決定(2)
次の等式が成り立つとき、$\triangle ABC$はどんな形の三角形か。
$\sin A\cos A=\sin B\cos B$
福田のわかった数学〜高校3年生理系077〜極値(1)極大値をもつ条件

単元:
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
この動画を見る
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
06滋賀県教員採用試験(数学:2番 三角関数)

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \leqq \pi,\ 0 \lt a$
$y=\sin2x+a(\sin\ x+\cos\ x)$の最大値、最小値を求めよ。
出典:滋賀県教員採用試験
この動画を見る
$0 \leqq x \leqq \pi,\ 0 \lt a$
$y=\sin2x+a(\sin\ x+\cos\ x)$の最大値、最小値を求めよ。
出典:滋賀県教員採用試験
14滋賀県教員採用試験(数学:2番 2変数関数の最大値、最小値)
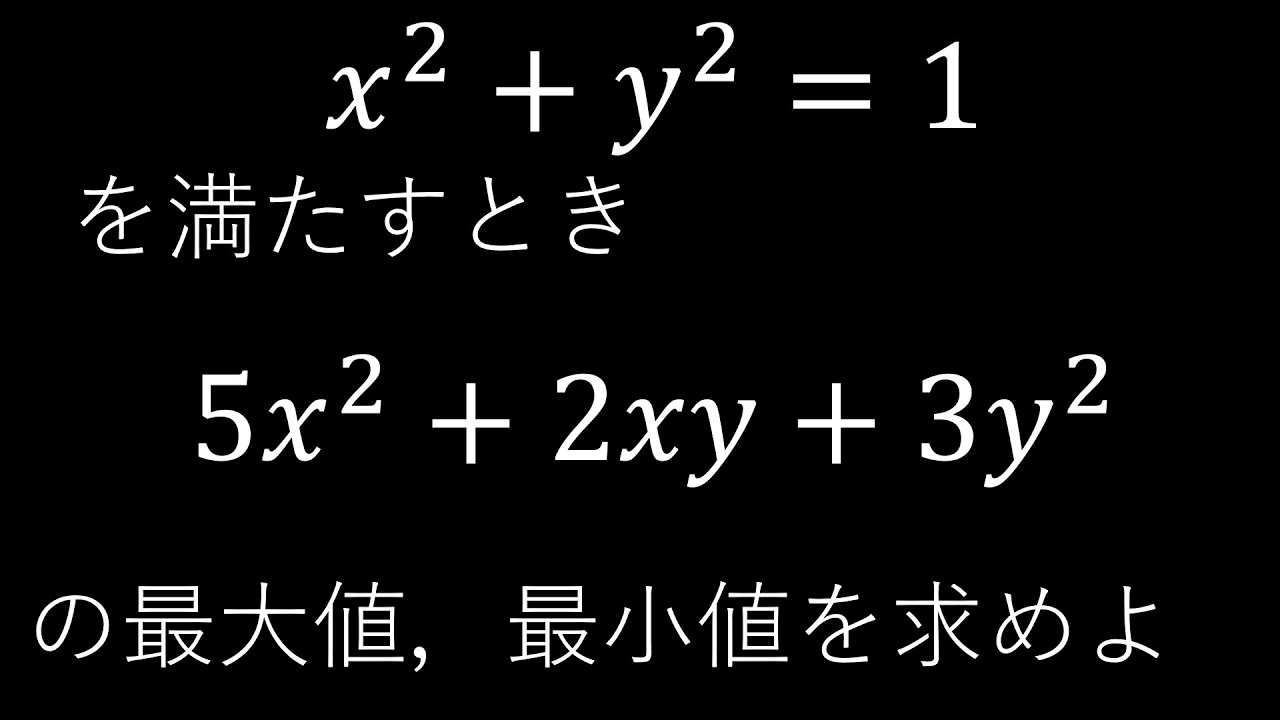
単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^2+y^2=1$をみたすとき
$5x^2+2xy+3y^2$の最大値、最小値を求めよ。
出典:滋賀県教員採用試験
この動画を見る
$x^2+y^2=1$をみたすとき
$5x^2+2xy+3y^2$の最大値、最小値を求めよ。
出典:滋賀県教員採用試験
大学入試問題#5 早稲田大学(2021) 三角関数

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{1}{2+\sin\alpha}+\displaystyle \frac{1}{2+\sin2\beta}=2$のとき
$|\alpha+\beta-8\pi|$の最小値を求めよ。
出典:2021年早稲田大学 入試問題
この動画を見る
$\displaystyle \frac{1}{2+\sin\alpha}+\displaystyle \frac{1}{2+\sin2\beta}=2$のとき
$|\alpha+\beta-8\pi|$の最小値を求めよ。
出典:2021年早稲田大学 入試問題
大学入試問題#2 早稲田大学(2021) 図形・三角関数・微分

単元:
#数Ⅱ#三角関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
半径1の円に外接する$AB=AC$の$\triangle ABC$において
$\angle BAC=2\theta$とする。
(1)$AC$を$\theta$で表せ
(2)$AC$が最小となるときの$\sin\theta$の値を求めよ。
出典:2021年早稲田大学 入試問題
この動画を見る
半径1の円に外接する$AB=AC$の$\triangle ABC$において
$\angle BAC=2\theta$とする。
(1)$AC$を$\theta$で表せ
(2)$AC$が最小となるときの$\sin\theta$の値を求めよ。
出典:2021年早稲田大学 入試問題
練習問題49 岡山大学(2021) 三角関数

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \leqq 2\pi$とする。
(1)
$\sin3x=-\sin\ x$を解け。
(2)
$\sin3x=\sin\ x$を解け。
(3)
$\sin3x \geqq a\ \sin\ x$が$-1 \leqq a \leqq 1$をみたす
すべての$a$に対して成り立つような$x$の値の範囲を求めよ。
出典:2021年岡山大学
この動画を見る
$0 \leqq x \leqq 2\pi$とする。
(1)
$\sin3x=-\sin\ x$を解け。
(2)
$\sin3x=\sin\ x$を解け。
(3)
$\sin3x \geqq a\ \sin\ x$が$-1 \leqq a \leqq 1$をみたす
すべての$a$に対して成り立つような$x$の値の範囲を求めよ。
出典:2021年岡山大学
関数の問題にみえて実は。。新田高校
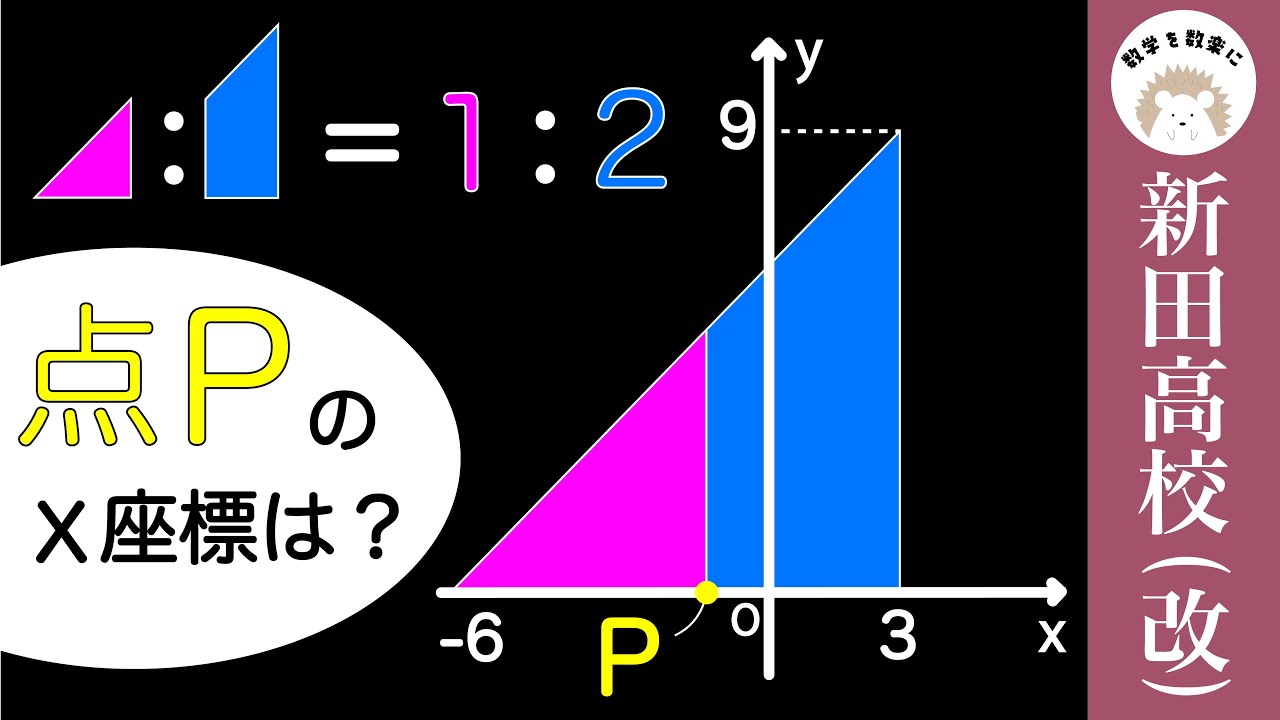
単元:
#数学(中学生)#数Ⅱ#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Pの座標は?
*図は動画内参照
新田高等学校
この動画を見る
点Pの座標は?
*図は動画内参照
新田高等学校
【数Ⅱ】高2生必見!! 2019年度8月 第2回 K塾高2模試 大問5_三角関数 (※(*)式に訂正あり)

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを正の整数とする。$\theta$の方程式$ \sin(a\theta)+\sqrt3\cos(a\theta)=1$ ・・・(*) がある。
(1)$\sin(\theta+\dfrac{\pi}{3}$)を$\sin\theta, \cos\theta$の式で表せ。
(2)$a=1$のとき、(*)を$0\leqq\theta\lt 2\pi$において表せ。
(3)(*)の$\theta\geqq 0$を満たすθのうち、小さい方から4つをaを用いて表せ。
(4)Nを正の整数とする。$0\leqq\lt 2\pi$において、(*)の解がちょうど2N個存在するようなaの値の範囲をNを用いて表せ。
この動画を見る
aを正の整数とする。$\theta$の方程式$ \sin(a\theta)+\sqrt3\cos(a\theta)=1$ ・・・(*) がある。
(1)$\sin(\theta+\dfrac{\pi}{3}$)を$\sin\theta, \cos\theta$の式で表せ。
(2)$a=1$のとき、(*)を$0\leqq\theta\lt 2\pi$において表せ。
(3)(*)の$\theta\geqq 0$を満たすθのうち、小さい方から4つをaを用いて表せ。
(4)Nを正の整数とする。$0\leqq\lt 2\pi$において、(*)の解がちょうど2N個存在するようなaの値の範囲をNを用いて表せ。
福田の数学〜中央大学2021年経済学部第1問(3)〜三角関数の最大

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}} (3)-\frac{\pi}{2} \leqq x \leqq \frac{\pi}{2}$
のとき、次の関数が最大値をとるときのxの値を求めよ。
$y=\sin x+\cos^2x$
2021中央大経済学部過去問
この動画を見る
${\Large\boxed{1}} (3)-\frac{\pi}{2} \leqq x \leqq \frac{\pi}{2}$
のとき、次の関数が最大値をとるときのxの値を求めよ。
$y=\sin x+\cos^2x$
2021中央大経済学部過去問
【数Ⅱ】高2生必見!! 2020年度 第2回 K塾高2模試 大問6_三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\theta$の関数。 $f(\theta)=\dfrac{1}{2\sin2\theta}-\sqrt2k\cos(θ-\dfrac{\pi}{4})+k^2$ がある。ただし、kは正の定数である。
(1)$\sin2\theta,\cos(\theta-\dfrac{\pi}{4})$のそれぞれをsinθ、cosθを用いて表せ。
(2)(i)$f(\theta)$を$(\sin\theta-p)(\cos\theta-q)$ (p,qは定数)の形で表せ。 $(ii)k=\dfrac{\sqrt3}{2}$のとき、方程式$f(\theta)=0$を$0\leqq \theta\lt 2\pi$において解け。
(3)$\theta$の方程式$f(\theta)=0$が$0\leqq\theta\lt 2\pi$において相異なる4個の解をもつようなkの値の範 囲を求めよ。
(4)(3)のとき、$\theta$の方程式$f(\theta)=0$の$0\leqq\theta\lt 2\pi$における最小の解を$\alpha$、最大の解を$\beta$と する。$\alpha+\beta=\dfrac{5\pi}{3}$となるようなkの値を求めよ。
この動画を見る
$\theta$の関数。 $f(\theta)=\dfrac{1}{2\sin2\theta}-\sqrt2k\cos(θ-\dfrac{\pi}{4})+k^2$ がある。ただし、kは正の定数である。
(1)$\sin2\theta,\cos(\theta-\dfrac{\pi}{4})$のそれぞれをsinθ、cosθを用いて表せ。
(2)(i)$f(\theta)$を$(\sin\theta-p)(\cos\theta-q)$ (p,qは定数)の形で表せ。 $(ii)k=\dfrac{\sqrt3}{2}$のとき、方程式$f(\theta)=0$を$0\leqq \theta\lt 2\pi$において解け。
(3)$\theta$の方程式$f(\theta)=0$が$0\leqq\theta\lt 2\pi$において相異なる4個の解をもつようなkの値の範 囲を求めよ。
(4)(3)のとき、$\theta$の方程式$f(\theta)=0$の$0\leqq\theta\lt 2\pi$における最小の解を$\alpha$、最大の解を$\beta$と する。$\alpha+\beta=\dfrac{5\pi}{3}$となるようなkの値を求めよ。
【数学Ⅲ/微分】三角関数の微分②(積の微分、2倍角の公式など)

単元:
#三角関数#微分法#数学(高校生)#数Ⅲ
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の関数を微分せよ。
(1)
$y=\displaystyle \frac{1}{\sin^2x}$
(2)
$y=x\sin3x$
(3)
$y=\sin x\cos x$
この動画を見る
次の関数を微分せよ。
(1)
$y=\displaystyle \frac{1}{\sin^2x}$
(2)
$y=x\sin3x$
(3)
$y=\sin x\cos x$
13和歌山県教員採用試験(数学:3番 三角関数)
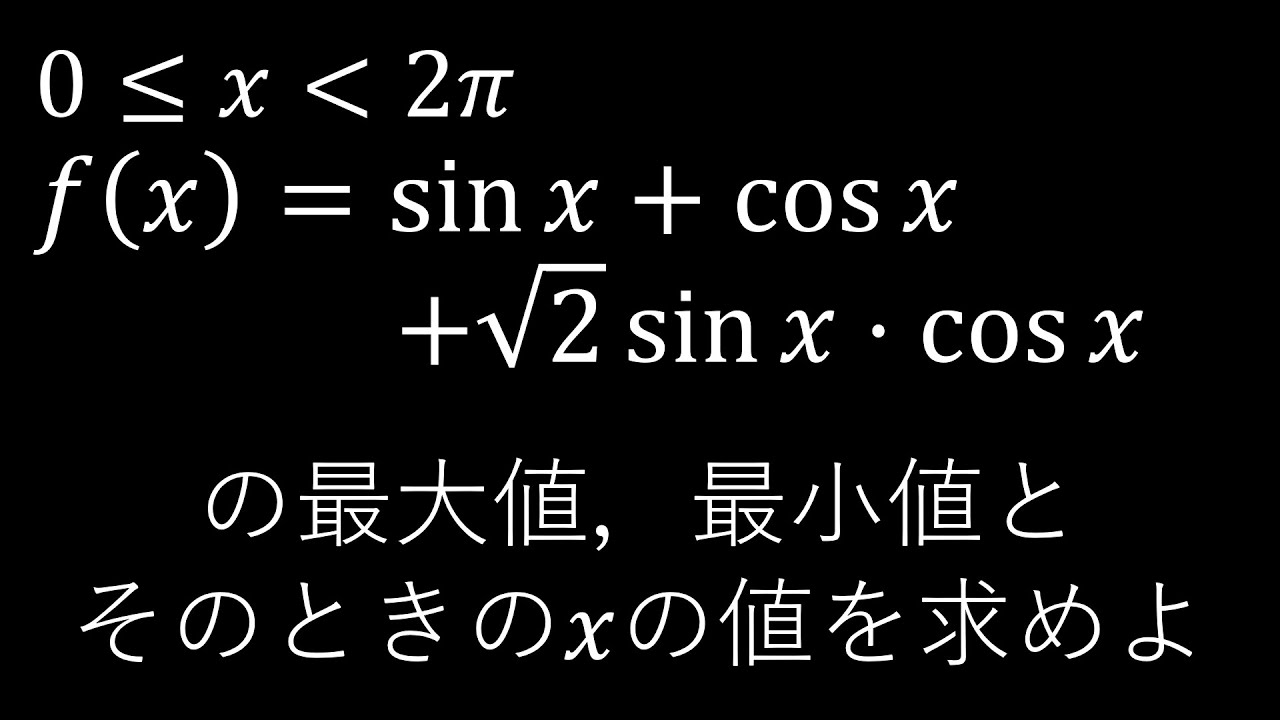
単元:
#数Ⅱ#三角関数#三角関数とグラフ#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$0\leqq x\lt 2\pi$である.
$f(x)=\sin x+\cos x+\sqrt 2 \sin x \cos x$の
最大値,最小値とそのときの$x$の値を求めよ.
この動画を見る
$\boxed{3}$
$0\leqq x\lt 2\pi$である.
$f(x)=\sin x+\cos x+\sqrt 2 \sin x \cos x$の
最大値,最小値とそのときの$x$の値を求めよ.
福田の数学〜慶應義塾大学2021年看護医療学部第1問(2)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#図形と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(2)$2(\cos\theta-\sin\theta)^2=1$を満たす$\theta$を$0 \leqq \theta \leqq \pi$の範囲で求めると$\boxed{\ \ イ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$
(2)$2(\cos\theta-\sin\theta)^2=1$を満たす$\theta$を$0 \leqq \theta \leqq \pi$の範囲で求めると$\boxed{\ \ イ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2021年薬学部第1問(4)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#図形と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(4)$\theta$は実数で、$-\frac{\pi}{2} \leqq \theta \leqq \frac{\pi}{2}$を満たす。方程式
$4\cos\frac{\theta}{2}(\cos\frac{\theta}{2}+\sin\frac{\theta}{2})=1$
を満たすとき、$\sin\theta+\cos\theta$の値は$\boxed{\ \ カ\ \ }$であり、
$\sin\theta$の値は$\boxed{\ \ キ\ \ }$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{1}}$(4)$\theta$は実数で、$-\frac{\pi}{2} \leqq \theta \leqq \frac{\pi}{2}$を満たす。方程式
$4\cos\frac{\theta}{2}(\cos\frac{\theta}{2}+\sin\frac{\theta}{2})=1$
を満たすとき、$\sin\theta+\cos\theta$の値は$\boxed{\ \ カ\ \ }$であり、
$\sin\theta$の値は$\boxed{\ \ キ\ \ }$である。
2021慶應義塾大学薬学部過去問
福田の数学〜慶應義塾大学2021年総合政策学部第2問〜見込む角の最大

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
サッカー選手Pは下図(※動画参照)のようにペナルティーエリアの左端の線を延長した線
のゴール寄り右3mをドリブルで敵陣にまっすぐ向かっている。Pがゴールに向かって
シュートするとき、Pから見てゴールの見える範囲が大きい方が得策である。すなわち、
下図(※動画参照)のような配置でh=3mのとき、選手Pが蹴り込める角度範囲である$\theta$
が最も大きくなるPのゴールラインからの距離xを求めたい。ただし、ゴールは下図のように
ペナルティーエリアの左右の中央で、ゴールラインの外側に設置されているものとする。
一般に図(※動画参照)のようにペナルティーエリアの左端からゴールの左端までの距離をa、
ペナルティーエリアの左端からゴールの右端までの距離をb、Pのドリブルのラインと
ペナルティーエリアの左端までの距離をh(ただし、$h \lt a$とする)、Pからゴールライン
をx、Pの正面から右のゴールポストまでの角度を$\alpha$、Pの正面から左のゴールポスト
までの角を$\beta$としたとき、次頁の解放の文章を完成させなさい。
(解法)$\tan\theta$を最も大きくするxを求める問題と考えることができる。
$\tan\theta=\tan\boxed{\ \ ア\ \ }=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}=\frac{\boxed{\ \ ア\ \ }×x}{x^2+\boxed{\ \ ウ\ \ }}$
$\tan\theta$の逆数を考えると、相加相乗平均の定理より
$\frac{1}{\tan\theta}=\frac{x}{\boxed{\ \ エ\ \ }}+\frac{\boxed{\ \ オ\ \ }}{x×\boxed{\ \ カ\ \ }} \geqq \frac{2}{\boxed{\ \ キ\ \ }}\sqrt{\boxed{\ \ ク\ \ }}$
であり、$\frac{1}{\tan\theta}$が最小、すなわち$\tan\theta$が最大となるのは$x=\sqrt{\boxed{\ \ ケ\ \ }}$のときである。
(解法終わり)
ペナルティエリアの横幅を40m、ゴールの横幅を8mとすると、今回のサッカー選手Pの場合、
$x=\sqrt{\boxed{\ \ コ\ \ }}m$のときに、$\theta$が最も大きくなることが分かる。
2021慶應義塾大学総合政策学部過去問
この動画を見る
${\Large\boxed{2}}$
サッカー選手Pは下図(※動画参照)のようにペナルティーエリアの左端の線を延長した線
のゴール寄り右3mをドリブルで敵陣にまっすぐ向かっている。Pがゴールに向かって
シュートするとき、Pから見てゴールの見える範囲が大きい方が得策である。すなわち、
下図(※動画参照)のような配置でh=3mのとき、選手Pが蹴り込める角度範囲である$\theta$
が最も大きくなるPのゴールラインからの距離xを求めたい。ただし、ゴールは下図のように
ペナルティーエリアの左右の中央で、ゴールラインの外側に設置されているものとする。
一般に図(※動画参照)のようにペナルティーエリアの左端からゴールの左端までの距離をa、
ペナルティーエリアの左端からゴールの右端までの距離をb、Pのドリブルのラインと
ペナルティーエリアの左端までの距離をh(ただし、$h \lt a$とする)、Pからゴールライン
をx、Pの正面から右のゴールポストまでの角度を$\alpha$、Pの正面から左のゴールポスト
までの角を$\beta$としたとき、次頁の解放の文章を完成させなさい。
(解法)$\tan\theta$を最も大きくするxを求める問題と考えることができる。
$\tan\theta=\tan\boxed{\ \ ア\ \ }=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}=\frac{\boxed{\ \ ア\ \ }×x}{x^2+\boxed{\ \ ウ\ \ }}$
$\tan\theta$の逆数を考えると、相加相乗平均の定理より
$\frac{1}{\tan\theta}=\frac{x}{\boxed{\ \ エ\ \ }}+\frac{\boxed{\ \ オ\ \ }}{x×\boxed{\ \ カ\ \ }} \geqq \frac{2}{\boxed{\ \ キ\ \ }}\sqrt{\boxed{\ \ ク\ \ }}$
であり、$\frac{1}{\tan\theta}$が最小、すなわち$\tan\theta$が最大となるのは$x=\sqrt{\boxed{\ \ ケ\ \ }}$のときである。
(解法終わり)
ペナルティエリアの横幅を40m、ゴールの横幅を8mとすると、今回のサッカー選手Pの場合、
$x=\sqrt{\boxed{\ \ コ\ \ }}m$のときに、$\theta$が最も大きくなることが分かる。
2021慶應義塾大学総合政策学部過去問
【高校数学】三角関数の公式~暗記不要なので証明しよう~ 4-4【数学Ⅱ】

【数Ⅱ】三角関数:加法定理の利用

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sinx - \siny =\dfrac{1}{2} , \cosx - \cosy =\dfrac{1}{3}$ , のとき、$\cos (x-y)$ の値を求めなさい。
この動画を見る
$\sinx - \siny =\dfrac{1}{2} , \cosx - \cosy =\dfrac{1}{3}$ , のとき、$\cos (x-y)$ の値を求めなさい。
【高校数学】三角関数のグラフの裏技~平行移動の場合~【数学Ⅱ】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
グラフを書け
1⃣
$y=\sin \theta+1$
2⃣
$y=2\sin(2\theta-\displaystyle \frac{\pi}{3})+1$
この動画を見る
グラフを書け
1⃣
$y=\sin \theta+1$
2⃣
$y=2\sin(2\theta-\displaystyle \frac{\pi}{3})+1$
【高校数学】三角関数の性質の裏技~先生には怒られるかもしれません~ 4-3.5【数学Ⅱ】

【数Ⅱ】三角関数:置換したときの解の個数を考える

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#チャート式#黄チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0\leqq\theta\lt2\pi$のとき、$\sin^2\theta-\sin\theta=a$ この方程式の解の個数を実数aの値で場合分けして求めよ
この動画を見る
$0\leqq\theta\lt2\pi$のとき、$\sin^2\theta-\sin\theta=a$ この方程式の解の個数を実数aの値で場合分けして求めよ
【数Ⅱ】三角関数:2021年高3第1回K塾記述模試

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは実数の定数とし、$0\leqq\theta\lt 2\pi$とする。次の2つの式を考える。
$8a\cos\theta- 8\cos2\theta=a^2+7$…①
$\sin\theta-\cos\theta\gt-1$…②
(1)a=1のとき、方程式①を解け。
(2)不等式②を 解け。
(3)(2)で求めた範囲に①の異なる解がちょうど3個存在するようなaの値の 範囲を求めよ。
この動画を見る
aは実数の定数とし、$0\leqq\theta\lt 2\pi$とする。次の2つの式を考える。
$8a\cos\theta- 8\cos2\theta=a^2+7$…①
$\sin\theta-\cos\theta\gt-1$…②
(1)a=1のとき、方程式①を解け。
(2)不等式②を 解け。
(3)(2)で求めた範囲に①の異なる解がちょうど3個存在するようなaの値の 範囲を求めよ。
福田の数学〜早稲田大学2021年商学部第1問(1)〜三角形と三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(1)三角形$\rm ABC$において、$\rm \angle B=2\alpha, \angle C=2\beta$とする。
$\tan\alpha\tan\beta=x, \rm \dfrac{AB+AC}{BC}=y$
とするとき、$y$を$x$で表すと、$y=\boxed{ア}$となる。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{1}}$
(1)三角形$\rm ABC$において、$\rm \angle B=2\alpha, \angle C=2\beta$とする。
$\tan\alpha\tan\beta=x, \rm \dfrac{AB+AC}{BC}=y$
とするとき、$y$を$x$で表すと、$y=\boxed{ア}$となる。
2021早稲田大学商学部過去問
福田のわかった数学〜高校3年生理系030〜極限(30)関数の極限、三角関数の極限(10)

単元:
#数Ⅱ#三角関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(10)
$\displaystyle \lim_{x \to 0}\frac{\sqrt{9-8x+7\cos2x}-(a+bx)}{x^2}$
が有限の値となる$a,b$とそのときの極限値
この動画を見る
数学$\textrm{III}$ 三角関数の極限(10)
$\displaystyle \lim_{x \to 0}\frac{\sqrt{9-8x+7\cos2x}-(a+bx)}{x^2}$
が有限の値となる$a,b$とそのときの極限値
福田の数学〜早稲田大学2021年社会科学部第1問〜三角関数で表された点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#三角関数#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ a,bを定数とし、関数$f(x)=x^2+ax+b$ とする。方程式$f(x)=0$の2つの解$\alpha,\beta\\$
が次式で与えられている。
$\alpha=\frac{\sin\theta}{1+\cos\theta}$, $\beta=\frac{\sin\theta}{1-\cos\theta}\\$
ここで$\theta$は、$0 \lt \theta \lt \pi$の定数である。次の問いに答えよ。
$(1)a,b$を$\theta$を用いて表せ。
$(2)\theta$が$0$ $\lt \theta \pi$で変化するとき、放物線$y=f(x)$の頂点の軌跡を求めよ。
$(3)\int_0^{2\sin\theta}f(x)dx=0$ となる$\theta$の値を全て求めよ。
2021早稲田大学社会科学部過去問
この動画を見る
${\Large\boxed{1}}$ a,bを定数とし、関数$f(x)=x^2+ax+b$ とする。方程式$f(x)=0$の2つの解$\alpha,\beta\\$
が次式で与えられている。
$\alpha=\frac{\sin\theta}{1+\cos\theta}$, $\beta=\frac{\sin\theta}{1-\cos\theta}\\$
ここで$\theta$は、$0 \lt \theta \lt \pi$の定数である。次の問いに答えよ。
$(1)a,b$を$\theta$を用いて表せ。
$(2)\theta$が$0$ $\lt \theta \pi$で変化するとき、放物線$y=f(x)$の頂点の軌跡を求めよ。
$(3)\int_0^{2\sin\theta}f(x)dx=0$ となる$\theta$の値を全て求めよ。
2021早稲田大学社会科学部過去問
