 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
大学入試問題#775「ほぼ、詰んでる」 横浜国立大学(1998) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi} x^2|\sin\ x|\ dx$
出典:1998年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi} x^2|\sin\ x|\ dx$
出典:1998年横浜国立大学 入試問題
全てのトークを諦めて積分を始めた瞬間 #shorts #高校数学 #積分
大学入試問題#774「基本的な良問」 横浜国立大学(1998) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e-1} \displaystyle \frac{log(log(x+1))}{x+1} dx$
出典:1998年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e-1} \displaystyle \frac{log(log(x+1))}{x+1} dx$
出典:1998年横浜国立大学 入試問題
#広島市立大学(2016) #定積分 #Shorts
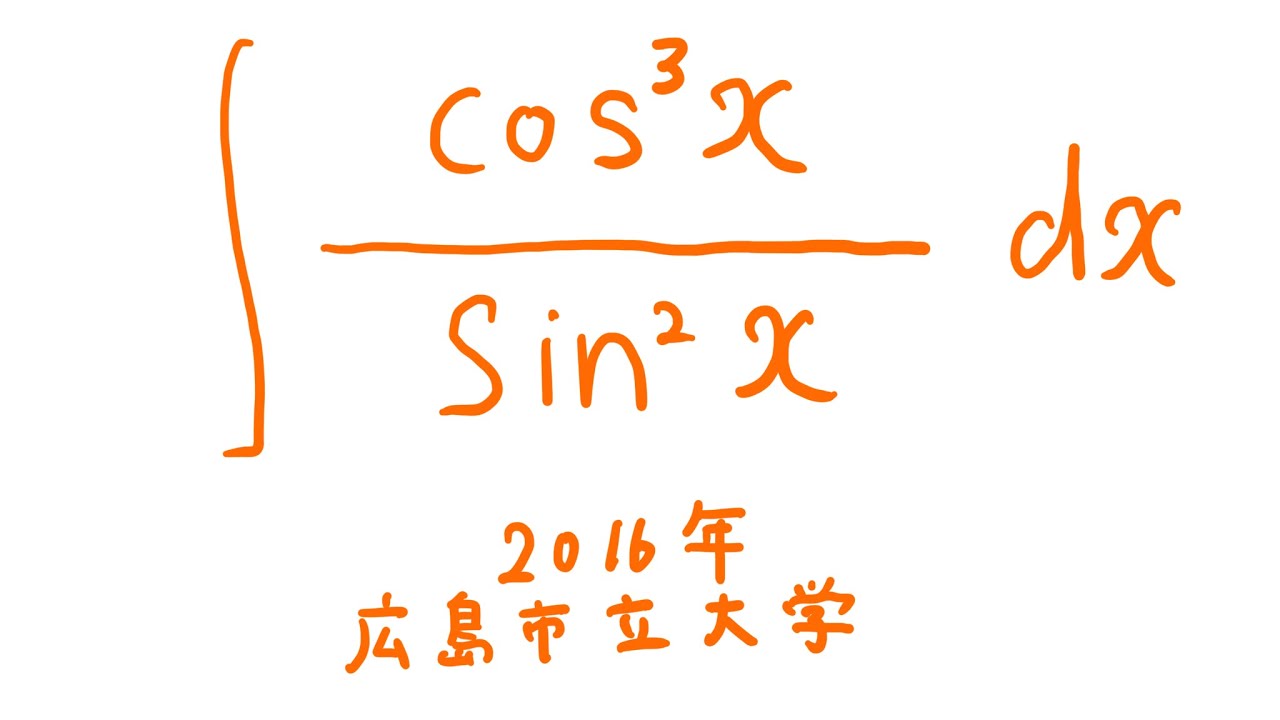
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
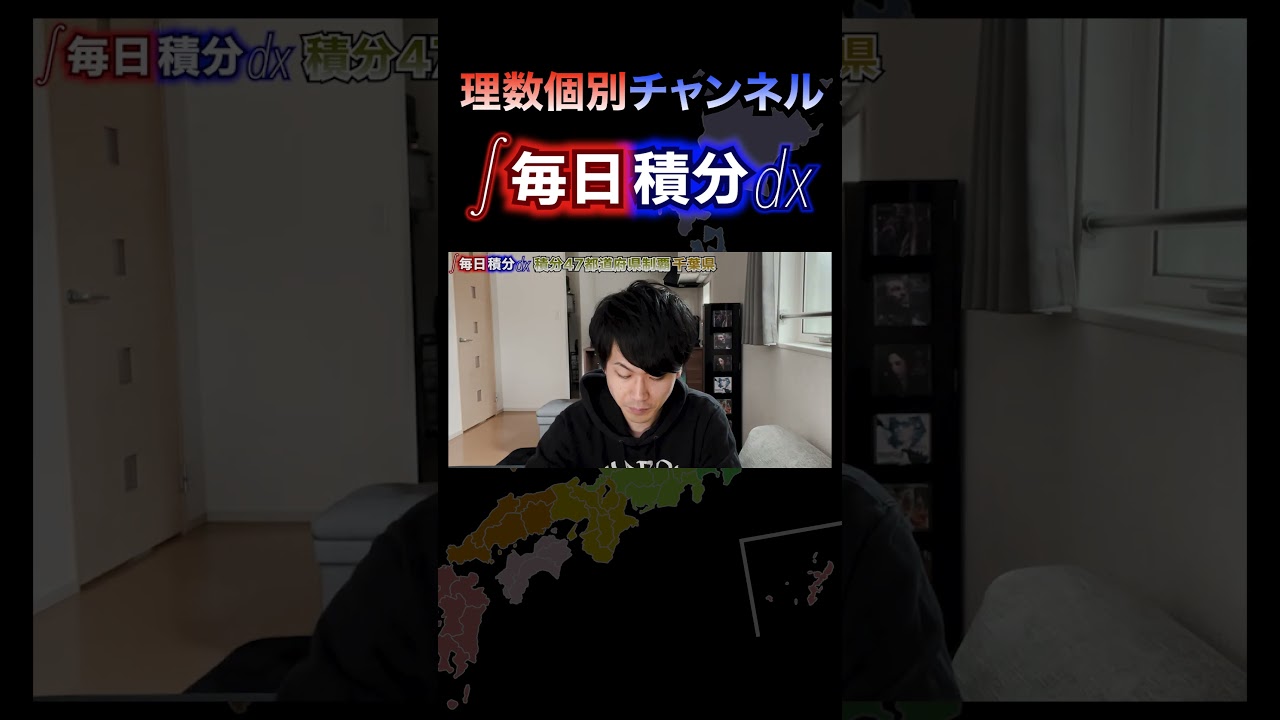
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2016年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2016年広島市立大学
大学入試問題#772「初手は好みがでそう」 広島市立大学(2012) #不定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{log\ x}{\sqrt[ 3 ]{ x }} dx$
出典:2012年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{log\ x}{\sqrt[ 3 ]{ x }} dx$
出典:2012年広島市立大学 入試問題
#会津大学(2023) #定積分 #Shorts
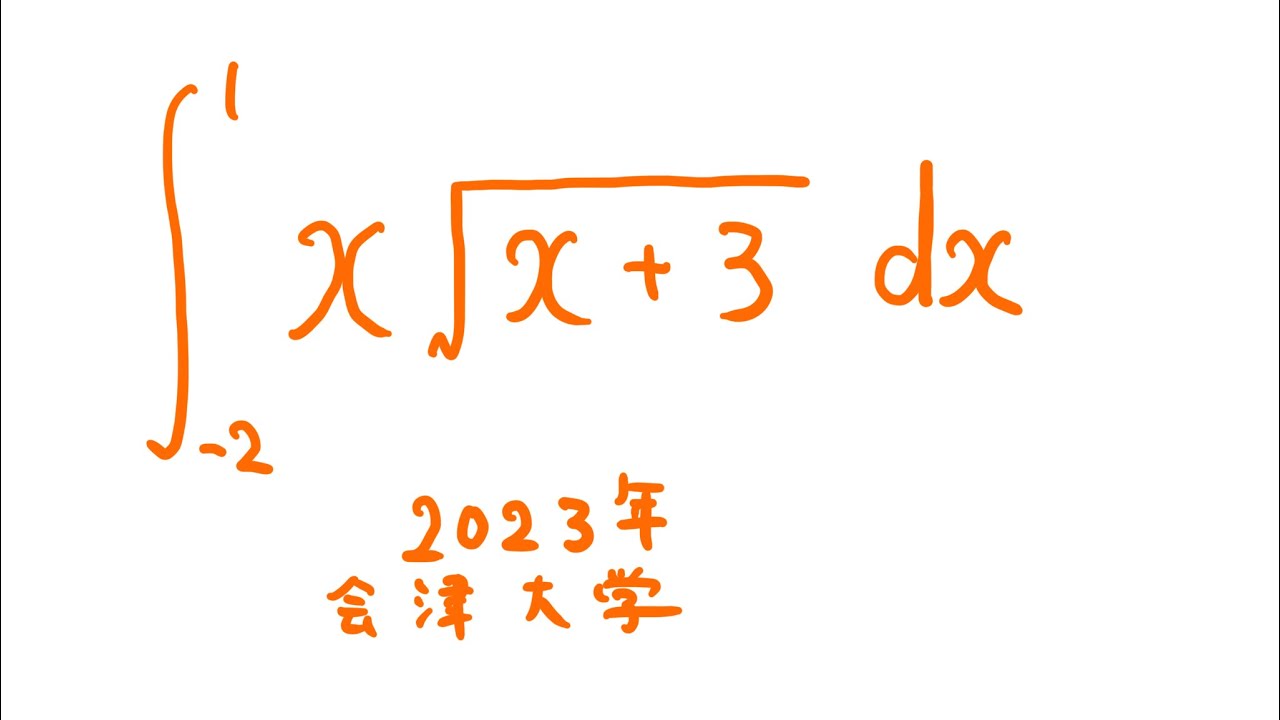
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-2}^{1} x\sqrt{ x+3 }\ dx$
出典:2023年会津大学
この動画を見る
$\displaystyle \int_{-2}^{1} x\sqrt{ x+3 }\ dx$
出典:2023年会津大学
大学入試問題#771「たぶん良問!」 島根大学後期(2023) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#島根大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1} dx$
出典:2023年島根大学後期 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1} dx$
出典:2023年島根大学後期 入試問題
#会津大学 2020年 #定積分 #Shorts
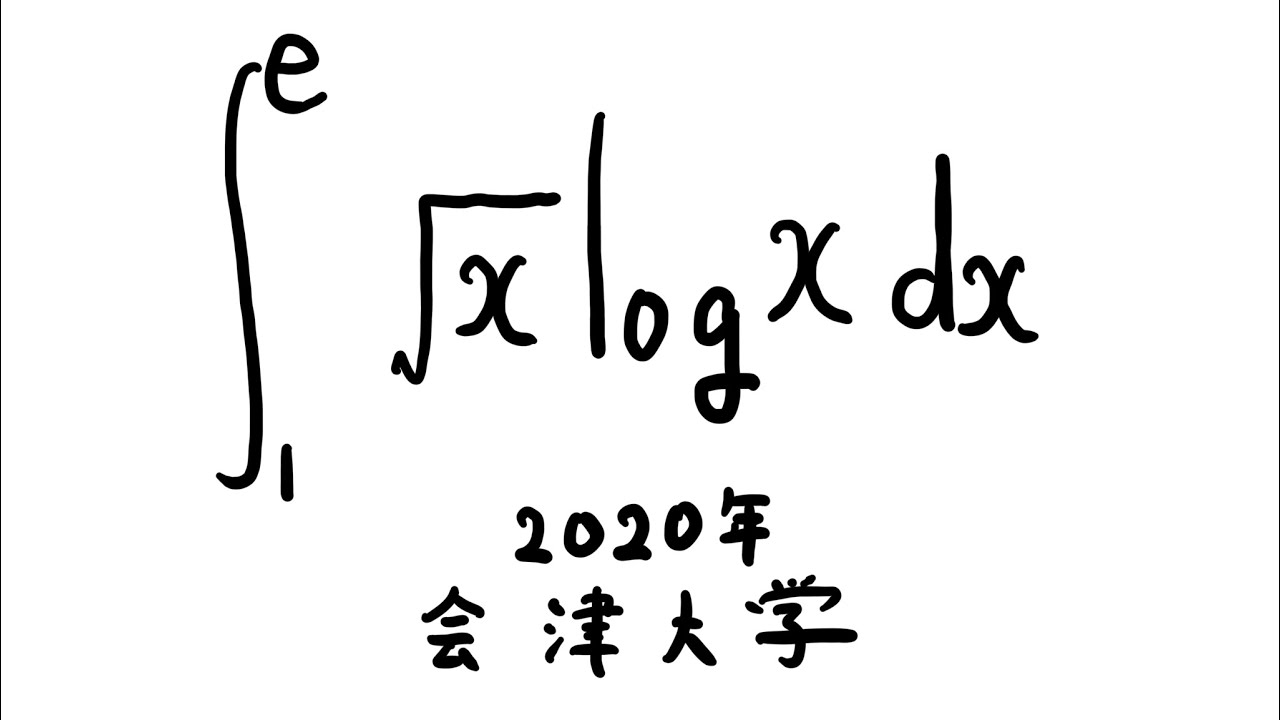
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} \sqrt{ x }\ log\ x\ dx$
出典:2020年会津大学
この動画を見る
$\displaystyle \int_{1}^{e} \sqrt{ x }\ log\ x\ dx$
出典:2020年会津大学
大学入試問題#770「減点注意!」 千葉大学(2003) #微積の応用

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a$は定数とし、$n$は2以上の整数とする。
関数$f(x)=ax^n log\ x-ax(x \gt 0)$の最小値が-1のとき、定積分$\displaystyle \int_{1}^{e} f(x)\ dx$の値を$n$と$e$を用いて表せ。
出典:2003年千葉大学 入試問題
この動画を見る
$a$は定数とし、$n$は2以上の整数とする。
関数$f(x)=ax^n log\ x-ax(x \gt 0)$の最小値が-1のとき、定積分$\displaystyle \int_{1}^{e} f(x)\ dx$の値を$n$と$e$を用いて表せ。
出典:2003年千葉大学 入試問題
【短時間でポイントチェック!!】定積分を含む等式から関数を求める問題〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$f(x)=2x^2+1+ \displaystyle \int_{0}^{1} xf(t) dt$
$f(x)$を求めよ。
この動画を見る
$f(x)=2x^2+1+ \displaystyle \int_{0}^{1} xf(t) dt$
$f(x)$を求めよ。
【短時間でポイントチェック!!】定積分を含む等式から関数を求める問題〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$f(x)=2x^2+1+\displaystyle \int_{0}^{1} xf(t)dt$
$f(x)$を求めよ
この動画を見る
$f(x)=2x^2+1+\displaystyle \int_{0}^{1} xf(t)dt$
$f(x)$を求めよ
#会津大学 2023年 #定積分 #Shorts
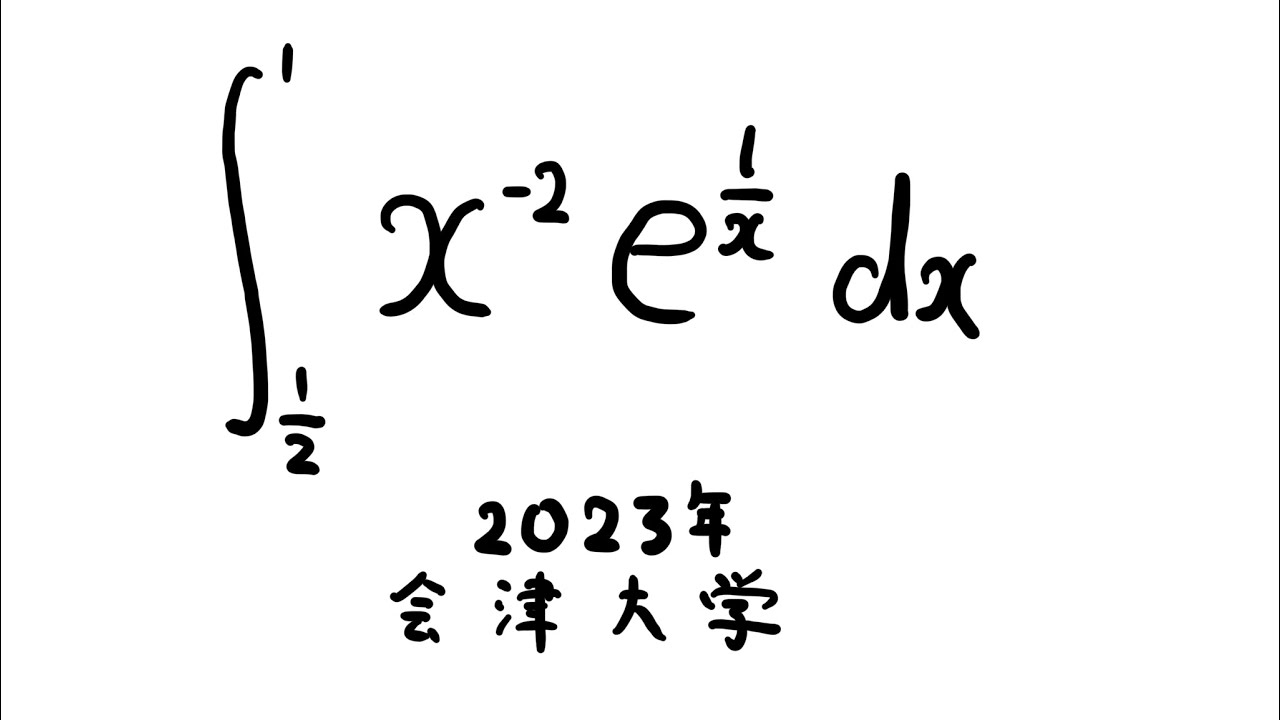
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{2}}^{1} x^{-2}e^{\frac{1}{x}} dx$
出典:2023年会津大学
この動画を見る
$\displaystyle \int_{\frac{1}{2}}^{1} x^{-2}e^{\frac{1}{x}} dx$
出典:2023年会津大学
大阪大学2023年の積分に見えない積分難問にガチで挑んでみた!#shorts #高校数学 #大阪大学
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大阪大学2023年の積分に見えない積分難問にガチで挑んでみた!
この動画を見る
大阪大学2023年の積分に見えない積分難問にガチで挑んでみた!
京都大学2024年の積分の問題をその場で解きながら解説してみた! #shorts #高校数学 #京都大学
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
京都大学2024年の積分の問題をその場で解きながら解説してみた!
この動画を見る
京都大学2024年の積分の問題をその場で解きながら解説してみた!
猫ミームで微分の定義に挑戦!

【短時間でポイントチェック!!】絶対値を含む定積分〔現役講師解説、数学〕

単元:
#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\int_1^3{|x^2-4|}dx$
この動画を見る
$\int_1^3{|x^2-4|}dx$
【短時間でポイントチェック!!】定積分 面積③ 曲線と曲線で囲まれた面積〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$y=x^2-2,y=-x^2-2x+2$で囲まれた部分の面積は?
この動画を見る
$y=x^2-2,y=-x^2-2x+2$で囲まれた部分の面積は?
【短時間でポイントチェック!!】定積分 面積② 直線と曲線で囲まれた面積〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$y=x^2-x-4,y=x-1$で囲まれた部分の面積
この動画を見る
$y=x^2-x-4,y=x-1$で囲まれた部分の面積
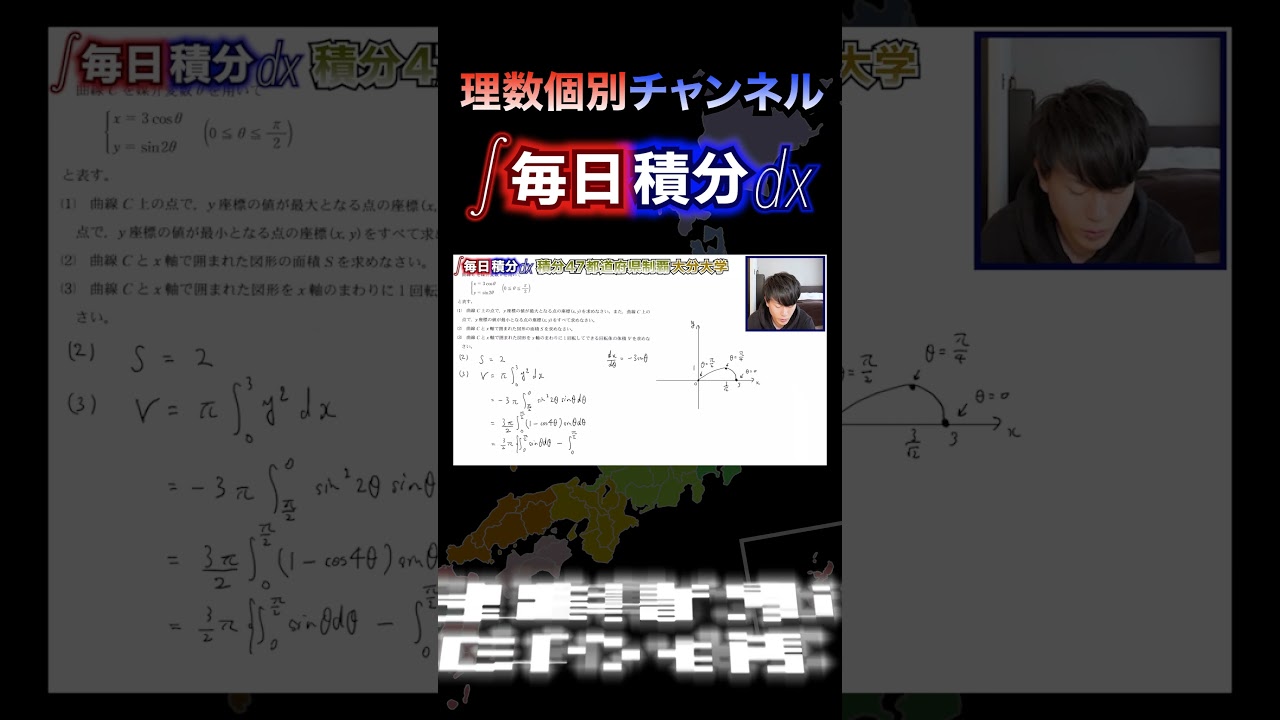
【高校数学】毎日積分76日目~47都道府県制覇への道~【⑲大阪】【毎日17時投稿】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
■【大阪大学 2023】
$n$を2以上の自然数とする。
(1)$0\leqq x\leqq 1$の時、次の不等式が成り立つことを示せ。
$\dfrac{1}{2}x^n\leqq (-1)^n\left[\dfrac{1}{x+1}-1-\displaystyle \sum_{k=2}^n(-1)^{k-1}\right]\leqq x^n-\dfrac{1}{2}x^{n+1}$
(2)$a_n=\displaystyle \sum_{k=1}^n\dfrac{(-1)^{k-1}}{k}$とするとき、次の極限値を求めよ。
$\lim_{n\to\infty}(-1)^n n(a_n-\log 2)$
この動画を見る
■【大阪大学 2023】
$n$を2以上の自然数とする。
(1)$0\leqq x\leqq 1$の時、次の不等式が成り立つことを示せ。
$\dfrac{1}{2}x^n\leqq (-1)^n\left[\dfrac{1}{x+1}-1-\displaystyle \sum_{k=2}^n(-1)^{k-1}\right]\leqq x^n-\dfrac{1}{2}x^{n+1}$
(2)$a_n=\displaystyle \sum_{k=1}^n\dfrac{(-1)^{k-1}}{k}$とするとき、次の極限値を求めよ。
$\lim_{n\to\infty}(-1)^n n(a_n-\log 2)$
【高校数学】毎日積分74日目~47都道府県制覇への道~【九州~四国・中国地方総集編(テーマ別)】【毎日17時投稿】

【短時間でポイントチェック!!】定積分 面積①〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$y=x^2-3x$と$x$軸および$x=1,x=4$で囲まれた面積は?
この動画を見る
$y=x^2-3x$と$x$軸および$x=1,x=4$で囲まれた面積は?
【高校数学】毎日積分70日目~国立大学47都道府県制覇への道~【⑭島根】【毎日17時投稿】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
■【島根大学 2023】
$a$を実数の定数、$n$を自然数とし、関数$f(x)$を$f(x)=1-ax^n$と定める。次の問いに答えよ。
(1)$\dfrac{n+5}{n+2}\leqq 2$を示せ。
(2)$\displaystyle \int_0^1 xf(x)dx\leqq \dfrac{2}{3}\displaystyle \int_0^1 f(x)dx^2$を示せ。
(3) (2)の不等式において、等号が成立するときの$a$と$n$の値を求めよ。
この動画を見る
■【島根大学 2023】
$a$を実数の定数、$n$を自然数とし、関数$f(x)$を$f(x)=1-ax^n$と定める。次の問いに答えよ。
(1)$\dfrac{n+5}{n+2}\leqq 2$を示せ。
(2)$\displaystyle \int_0^1 xf(x)dx\leqq \dfrac{2}{3}\displaystyle \int_0^1 f(x)dx^2$を示せ。
(3) (2)の不等式において、等号が成立するときの$a$と$n$の値を求めよ。
【高校数学】毎日積分65日目~47都道府県制覇への道~【⑨高知】【毎日17時投稿】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)すべての実数xに対して
$\sin 3x=3\sin x-4\sin^3x$
$\cos 3x=-3\cos x+4\cos^3x$
が成り立つことを、加法定理と2倍角の公式を用いて示せ。
(2)実数$\theta$を、$\dfrac{\pi}{3}\lt \theta \lt \dfrac{\pi}{2}$と$\cos 3\theta=-\dfrac{11}{16}$を同時に満たすものとする。このとき、$\cos\theta$を求めよ。
(3)(2)の$\theta$に対して、定積分$\displaystyle \int_{0}^{\theta}sin^5x dx$を求めよ。
【高知大学 2023】
この動画を見る
(1)すべての実数xに対して
$\sin 3x=3\sin x-4\sin^3x$
$\cos 3x=-3\cos x+4\cos^3x$
が成り立つことを、加法定理と2倍角の公式を用いて示せ。
(2)実数$\theta$を、$\dfrac{\pi}{3}\lt \theta \lt \dfrac{\pi}{2}$と$\cos 3\theta=-\dfrac{11}{16}$を同時に満たすものとする。このとき、$\cos\theta$を求めよ。
(3)(2)の$\theta$に対して、定積分$\displaystyle \int_{0}^{\theta}sin^5x dx$を求めよ。
【高知大学 2023】
【短時間でポイントチェック!!】定積分 1/6公式〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\int_{-1}^2\{(x+2)-x^2\}dx$
この動画を見る
$\int_{-1}^2\{(x+2)-x^2\}dx$
故郷長崎の積分でまさかの大苦戦…!? #shorts #高校数学 #毎日積分
毎日積分~47都道府県制覇への道~ #Shorts #高校数学 #積分
【短時間でポイントチェック!!】定積分の基礎〔現役講師解説、数学〕

毎日積分~積分47都道府県制覇への道~ #Shorts #毎日積分 #高校数学
【短時間でポイントチェック!!】不定積分の基礎〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
①$\int xdx$
②$\int x^2dx$
③$\int 4x^2dx$
④$\int (x^2+x)dx$
⑤$\int 1dx$
この動画を見る
①$\int xdx$
②$\int x^2dx$
③$\int 4x^2dx$
④$\int (x^2+x)dx$
⑤$\int 1dx$
【積分】積分がなぜ面積を求められるのかについて解説しました!【数学III】

