 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
【数Ⅱ】微分法と積分法:平均変化率について学ぼう!

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・$y=3x+1$のxが1から4まで増加するときの変化の割合(平均変化率)は?
・$y=2x^2$が1から4まで増加するときの変化の割合(平均変化率)は?
この動画を見る
・$y=3x+1$のxが1から4まで増加するときの変化の割合(平均変化率)は?
・$y=2x^2$が1から4まで増加するときの変化の割合(平均変化率)は?
07神奈川県教員採用試験(数学:9番 領域と最小値)

単元:
#数Ⅱ#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{9}$
$x^2+xy-2y^2+6y-4\geqq 0$
$x^2+y^2$の最小値を求めよ.
この動画を見る
$\boxed{9}$
$x^2+xy-2y^2+6y-4\geqq 0$
$x^2+y^2$の最小値を求めよ.
練習問題9(数検準1級 教員採用試験 極限値からの区分求積法)【難】
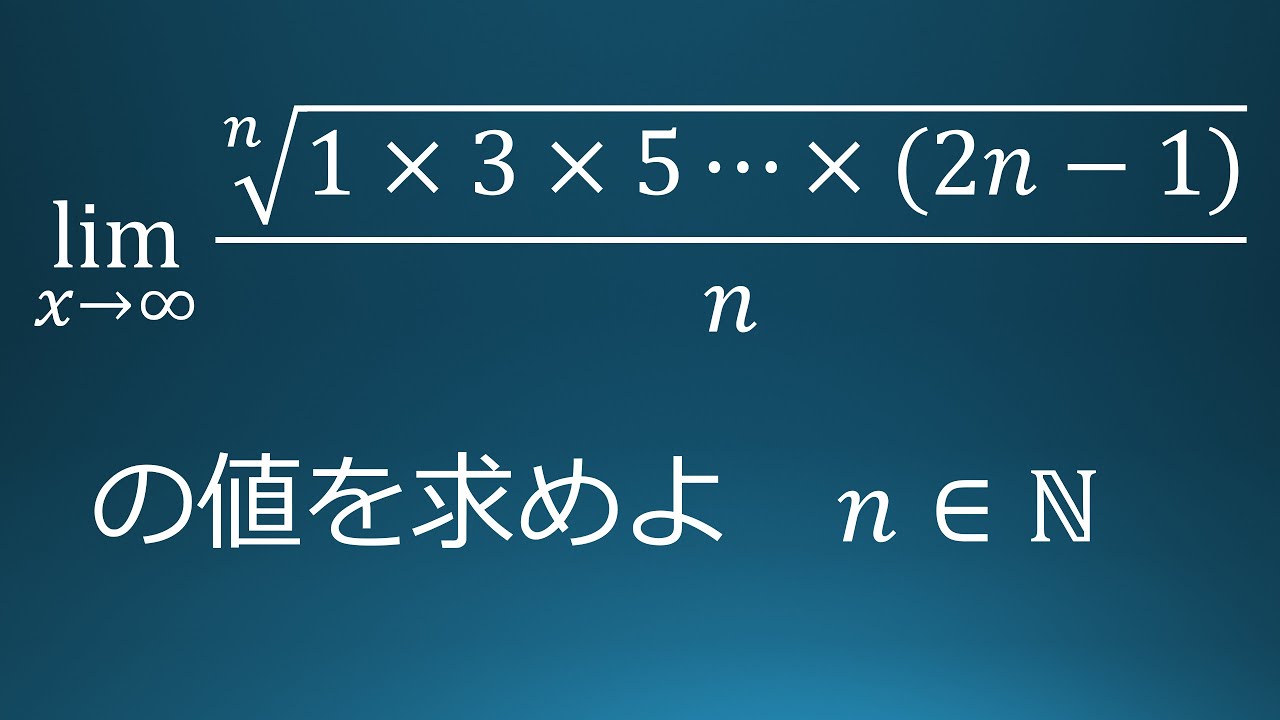
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
限値からの区分求積法を解説していきます.
この動画を見る
限値からの区分求積法を解説していきます.
練習問題8(数検準1級 教員採用試験 極限値からの区分求積法)
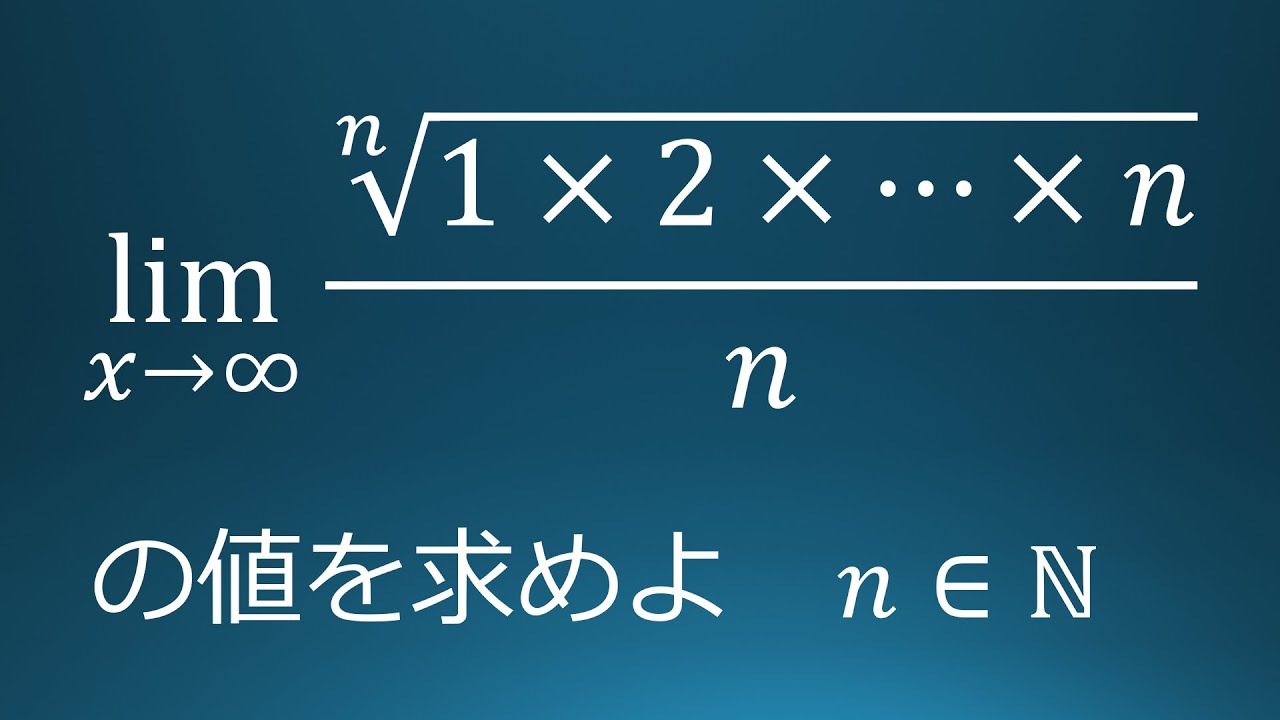
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \dfrac{\sqrt[n]{1\times 3\times 5\times ・・・ \times(2n-1)}}{n}$
これを解け.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{\sqrt[n]{1\times 3\times 5\times ・・・ \times(2n-1)}}{n}$
これを解け.
練習問題7(数検準1級 教員採用試験 極限値)
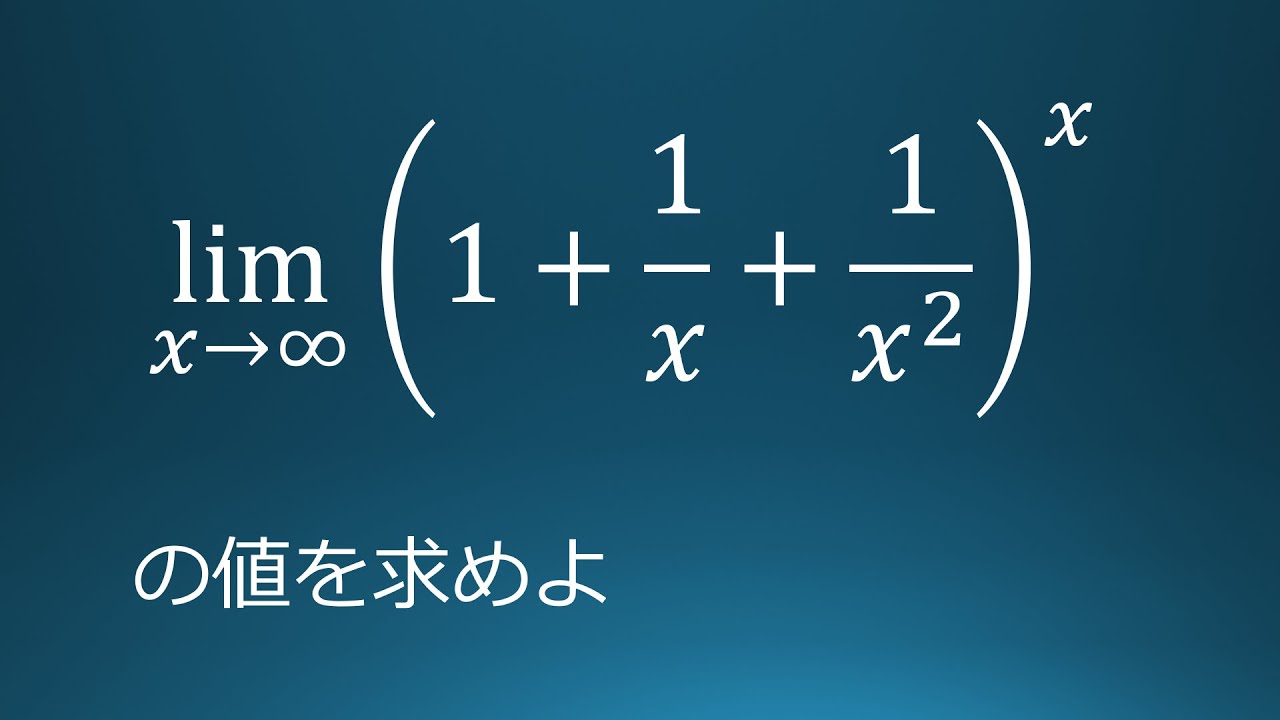
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty} \left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)^x$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\infty} \left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)^x$
これを解け.
練習問題6(数検準1級 教員採用試験 極限値【やや難】)
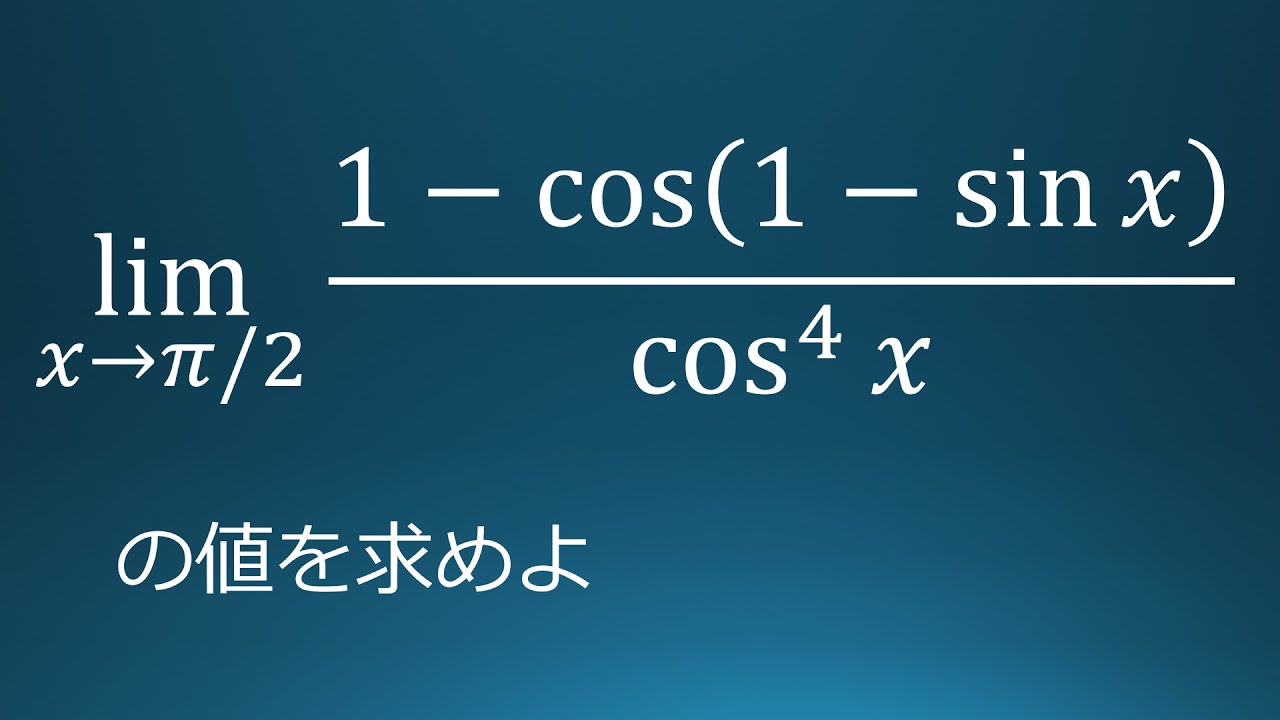
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\frac{\pi}{2}} \dfrac{1-\cos(1-\sin x)}{\cos^4x}$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\frac{\pi}{2}} \dfrac{1-\cos(1-\sin x)}{\cos^4x}$
これを解け.
練習問題5(数検準1級 教員採用試験 極限値)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty} \dfrac{\tan^3x-\sin^3x}{x^5}$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\infty} \dfrac{\tan^3x-\sin^3x}{x^5}$
これを解け.
数検準1級1次(5番 積分)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$これを解け.
(1)$\displaystyle \int_{}^{} \dfrac{1}{x^2\ e^{\frac{1}{x}}}$
(2)$\displaystyle \int_{\frac{1}{2}}^{1}\dfrac{1}{x^2\ e^{\frac{1}{2}}}$
この動画を見る
$\boxed{5}$これを解け.
(1)$\displaystyle \int_{}^{} \dfrac{1}{x^2\ e^{\frac{1}{x}}}$
(2)$\displaystyle \int_{\frac{1}{2}}^{1}\dfrac{1}{x^2\ e^{\frac{1}{2}}}$
数検準1級1次(7番 極限値)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$ $\displaystyle \lim_{x\to 0}\ \dfrac{1}{x}\left(\frac{1}{\sin x}-\dfrac{1}{\tan x}\right)$
これを解け.
この動画を見る
$\boxed{7}$ $\displaystyle \lim_{x\to 0}\ \dfrac{1}{x}\left(\frac{1}{\sin x}-\dfrac{1}{\tan x}\right)$
これを解け.
08愛知県教員採用試験(数学:9番 区分求積法)

数検準1級2次過去問【2020年12月】7番:微積 良問

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}\ f(x)=\dfrac{\sin x+a}{x}$ $(x \gt 0)$は$0\lt x\lt 2\pi$で極値をもつ.
(1)$a$の値の範囲を求めよ.
(2)$f(x)$が$o\lt x\lt 2\pi$で、極大値$\dfrac{1}{2}$をもつとき,$a$の値を求めよ.
この動画を見る
$\boxed{7}\ f(x)=\dfrac{\sin x+a}{x}$ $(x \gt 0)$は$0\lt x\lt 2\pi$で極値をもつ.
(1)$a$の値の範囲を求めよ.
(2)$f(x)$が$o\lt x\lt 2\pi$で、極大値$\dfrac{1}{2}$をもつとき,$a$の値を求めよ.
山形大 積分

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a\gt 0$である.
$f(x)=x^4-6a^2x^2+5a^4(a,0)$における接線$\ell$と$f(x)$とで囲まれる面積を求めよ.
山形大過去問
この動画を見る
$a\gt 0$である.
$f(x)=x^4-6a^2x^2+5a^4(a,0)$における接線$\ell$と$f(x)$とで囲まれる面積を求めよ.
山形大過去問
【数Ⅱ】微分法と積分法:定積分について基礎からめちゃめちゃ分かりやすく解説!用語や記号の解説からしますので初学者必見!

【数Ⅱ】微分法と積分法:不定積分について基礎からめちゃめちゃ分かりやすく解説!用語や記号の解説からしますので初学者必見!

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
不定積分$\int_{}^{}(3x^2-4x+4)dx$を計算しなさい.
この動画を見る
不定積分$\int_{}^{}(3x^2-4x+4)dx$を計算しなさい.
15京都府教員採用試験(数学:3番 微分)

単元:
#数Ⅱ#微分法と積分法#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣ A(1,a)から曲線$C:y=x^3+3x^2+x$に異なる接線が3本引けるようにaの範囲を定めよ
この動画を見る
3⃣ A(1,a)から曲線$C:y=x^3+3x^2+x$に異なる接線が3本引けるようにaの範囲を定めよ
13兵庫県教員採用試験(数学:2番 微分)

単元:
#数Ⅱ#微分法と積分法#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣
$C_1:y=x^2-4x+36$ , $C_2:y=4x^2+8x$の共通接線の方程式を求めよ。
この動画を見る
2⃣
$C_1:y=x^2-4x+36$ , $C_2:y=4x^2+8x$の共通接線の方程式を求めよ。
15兵庫県教員採用試験(数学:3番 微積)

単元:
#数Ⅱ#微分法と積分法#その他#面積、体積#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣ $k>0$ , $C:f(x)=x^3-3k^2x$
Cは極大値16をもつ。C上の点(1,f(1))の接線lとCで囲まれた面積Sを求めよ。
この動画を見る
3⃣ $k>0$ , $C:f(x)=x^3-3k^2x$
Cは極大値16をもつ。C上の点(1,f(1))の接線lとCで囲まれた面積Sを求めよ。
19奈良県教員採用試験(数学:2番 三角関数)

単元:
#数Ⅱ#三角関数#三角関数とグラフ#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣$0 \leqq θ \leqq \pi$
$y= sin2θ + 2(sinθ+cosθ)-i$のMAX、minとそのときのθの値を求めよ。
この動画を見る
2⃣$0 \leqq θ \leqq \pi$
$y= sin2θ + 2(sinθ+cosθ)-i$のMAX、minとそのときのθの値を求めよ。
【数Ⅱ】微分法と積分法:関数の極大・極小 関数f(x)=x³-3x²+2のグラフを描け!!

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#高校ゼミスタンダード#高校ゼミスタンダード数Ⅱ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数f(x)=x³-3x²+2のグラフを描け
この動画を見る
関数f(x)=x³-3x²+2のグラフを描け
18愛知県教員採用試験(数学:8番 面積の最小値)

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
8⃣(1,0)を通る直線lと$y=x^2-2$で囲まれる図形の面積Sの最小値を求めよ。
この動画を見る
8⃣(1,0)を通る直線lと$y=x^2-2$で囲まれる図形の面積Sの最小値を求めよ。
【理数個別の過去問解説】2012年度京都大学 数学 第3問解説

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
京都大学(文理共通)2012年第3問
実数x,yが条件x²+xy+y²=6を満たしながら動くとき、x²y+xy²-x²-2xy-y²+x+y がとりうる値の範囲を求めよ。
この動画を見る
京都大学(文理共通)2012年第3問
実数x,yが条件x²+xy+y²=6を満たしながら動くとき、x²y+xy²-x²-2xy-y²+x+y がとりうる値の範囲を求めよ。
【理数個別の過去問解説】2016年度京都大学 数学 文系第1問解説

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
京都大学(文系)2016年第1問
xy平面内の領域 $x²+y²≦2, |x|≦1$で,曲線$C:y=x³+x²-x $の上側にある部分の面積を求めよ。
この動画を見る
京都大学(文系)2016年第1問
xy平面内の領域 $x²+y²≦2, |x|≦1$で,曲線$C:y=x³+x²-x $の上側にある部分の面積を求めよ。
【理数個別の過去問解説】2018年度一橋大学 数学 第5問解説

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#一橋大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
一橋大学2018年第5問
aを実数とし, $f(x)=x-x³,g(x)=a(x-x²)$とする。2つの曲線$y=f(x),y=g(x)$は$0<x<1$の範囲に共有点をもつ。
(1)aのとりうる値の範囲を求めよ。
(2)y=f(x)とy=g(x)で囲まれた2つの部分の面積が等しくなるようなaの値を求めよ。
この動画を見る
一橋大学2018年第5問
aを実数とし, $f(x)=x-x³,g(x)=a(x-x²)$とする。2つの曲線$y=f(x),y=g(x)$は$0<x<1$の範囲に共有点をもつ。
(1)aのとりうる値の範囲を求めよ。
(2)y=f(x)とy=g(x)で囲まれた2つの部分の面積が等しくなるようなaの値を求めよ。
【数Ⅱ】微分法と積分法:立体図形の見方・捉え方を千葉大の過去問の類題を例に説明します!!

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
教材:
#7つの大解法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
四面体OABCにおいて、$OA=OB=OC=1、∠BAC=90°$のとき、この四面体の体積Vの最大値を求めよ。
この動画を見る
四面体OABCにおいて、$OA=OB=OC=1、∠BAC=90°$のとき、この四面体の体積Vの最大値を求めよ。
長崎大 積分

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=-x^4+8x^3-18x^2+11$と異なる2点で接する直線と$f(x)$で囲まれる面積を求めよ.
長崎大過去問
この動画を見る
$f(x)=-x^4+8x^3-18x^2+11$と異なる2点で接する直線と$f(x)$で囲まれる面積を求めよ.
長崎大過去問
17神奈川県教員採用試験(数学:8番 積分【面積の最小値】)

単元:
#数Ⅱ#2次関数#複素数と方程式#2次関数とグラフ#微分法と積分法#解と判別式・解と係数の関係#面積、体積#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
8⃣$y=x^2$と(-1,3)を通る直線lで囲まれた面積Sの最小値を求めよ。
この動画を見る
8⃣$y=x^2$と(-1,3)を通る直線lで囲まれた面積Sの最小値を求めよ。
【数Ⅱ】微分法と積分法:偶関数・奇関数の性質の利用!知っているか知らないかで、差がつきますよ!!

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
偶関数・奇関数の性質を利用すると、定積分の計算が簡単になる!?なぜそうなるか、グラフのイメージと共に解説します!
この動画を見る
偶関数・奇関数の性質を利用すると、定積分の計算が簡単になる!?なぜそうなるか、グラフのイメージと共に解説します!
17奈良県教員採用試験(数学:高校4番 微分・式変形)

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
4⃣ $f(x)=x^3-3x^2+6$
異なる2点A(α,f(α)),B(β,f(β))上の接線は平行
(1)βをαで表せ
(2)直線ABをαを用いて表せ
(3)直線ABは定点を通ることを示せ
この動画を見る
4⃣ $f(x)=x^3-3x^2+6$
異なる2点A(α,f(α)),B(β,f(β))上の接線は平行
(1)βをαで表せ
(2)直線ABをαを用いて表せ
(3)直線ABは定点を通ることを示せ
中央大2020微分 3次関数と直線の交点

単元:
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3+3x^2-2$と$y=k(x-1)-2$が相異なる3点で交わる$k$の範囲を求めよ.
2020中央大(経)過去問
この動画を見る
$f(x)=x^3+3x^2-2$と$y=k(x-1)-2$が相異なる3点で交わる$k$の範囲を求めよ.
2020中央大(経)過去問
早稲田大2019微分・3次関数と直線の交点

単元:
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=x^2$上の$(a,a^2)$における接線が$y=x^3-ax$と3点で交わる$a$の範囲を求めよ.
2019早稲田大過去問
この動画を見る
$y=x^2$上の$(a,a^2)$における接線が$y=x^3-ax$と3点で交わる$a$の範囲を求めよ.
2019早稲田大過去問
