微分法と積分法
微分法と積分法
【高校数学】 数Ⅱ－１６０ 関数の最大値・最小値⑤
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①関数$f(x)=x^3-3ax^2+5a^3$の$0 \leqq x \leqq 3$における最小値を求めよう。
ただし、$a \gt 0$とする。
この動画を見る
①関数$f(x)=x^3-3ax^2+5a^3$の$0 \leqq x \leqq 3$における最小値を求めよう。
ただし、$a \gt 0$とする。
【高校数学】 数Ⅱ－１５９ 関数の最大値・最小値④
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$a \gt 0$とする。
関数$f(x)=ax^3+3ax^2+b(-1 \leqq x \leqq 2)$の最大値が10、最小値が-8であるとき、定数a,bの値を求めよう。
この動画を見る
①$a \gt 0$とする。
関数$f(x)=ax^3+3ax^2+b(-1 \leqq x \leqq 2)$の最大値が10、最小値が-8であるとき、定数a,bの値を求めよう。
【高校数学】 数Ⅱ－１５８ 関数の最大値・最小値③
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$0 \leqq x \lt 2π$のとき、関数$y=\cos 2x-2\cos^3x$の最大値と最小値、およびそのときのxの値を求めよう。
この動画を見る
①$0 \leqq x \lt 2π$のとき、関数$y=\cos 2x-2\cos^3x$の最大値と最小値、およびそのときのxの値を求めよう。
【高校数学】 数Ⅱ－１５７ 関数の最大値・最小値②
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎$x+3y=9.x \geqq 0、y \geqq 0$のとき、次の問いに答えよう。
①xのとりうる値の範囲を求めよう。
②$x^2y$の最大値と最小値、およびそのときのx,yの値を求めよう。
この動画を見る
◎$x+3y=9.x \geqq 0、y \geqq 0$のとき、次の問いに答えよう。
①xのとりうる値の範囲を求めよう。
②$x^2y$の最大値と最小値、およびそのときのx,yの値を求めよう。
【高校数学】 数Ⅱ－１５６ 関数の最大値・最小値①
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の関数の最大値と最小値を求めよう。
①$y=-2x^3+6x^2-10 (-2 \leqq x \leqq 3)$
②$y=x-4x²+12(-1 \leqq x \leqq 4)$
この動画を見る
◎次の関数の最大値と最小値を求めよう。
①$y=-2x^3+6x^2-10 (-2 \leqq x \leqq 3)$
②$y=x-4x²+12(-1 \leqq x \leqq 4)$
【高校数学】 数Ⅱ－１５５ 関数の極値⑤
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の条件を満たすような、定数aの値の範囲をそれぞれ求めよう。
①関数$f(x)=x^3+ax^2+3x$が常に単調に増加する。
②関数$f(x)=x^3+3ax^2+3(a+2)x+1$が極値をもつ。
この動画を見る
◎次の条件を満たすような、定数aの値の範囲をそれぞれ求めよう。
①関数$f(x)=x^3+ax^2+3x$が常に単調に増加する。
②関数$f(x)=x^3+3ax^2+3(a+2)x+1$が極値をもつ。
【高校数学】 数Ⅱ－１５４ 関数の極値④
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①関数$f(x)=x^2-4x^2+ax$が$x=2$で極小値をとるとき、aの値を求めよう。
②$x=-1$で極大値5、$x=1$で極小値1をとるような3次関数f(x)を求めよう。
この動画を見る
①関数$f(x)=x^2-4x^2+ax$が$x=2$で極小値をとるとき、aの値を求めよう。
②$x=-1$で極大値5、$x=1$で極小値1をとるような3次関数f(x)を求めよう。
【高校数学】 数Ⅱ－１５３ 関数の極値③
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の関数の極値を求めて、そのグラフをかこう。
①$y=3x^4-4x^3-12x^2$
②$y=x^4+2x^3+1$
この動画を見る
◎次の関数の極値を求めて、そのグラフをかこう。
①$y=3x^4-4x^3-12x^2$
②$y=x^4+2x^3+1$
【高校数学】 数Ⅱ－１５２ 関数の極値②
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の関数の極値を求めて、そのグラフをかこう。
①$y =x^3+6x^2+12x+5$
②$y=x^4-6x^2+2$
この動画を見る
◎次の関数の極値を求めて、そのグラフをかこう。
①$y =x^3+6x^2+12x+5$
②$y=x^4-6x^2+2$
【高校数学】 数Ⅱ－１５１ 関数の極値①
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の関数の極値を求めて、そのグラフをかこう。
①$y=x^3-3x^2-9x+11$
②$y=-x^3+3x$
この動画を見る
◎次の関数の極値を求めて、そのグラフをかこう。
①$y=x^3-3x^2-9x+11$
②$y=-x^3+3x$
【高校数学】 数Ⅱ－１５０ 関数の値の変化
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の関数の増減を調べよう。
①$y=2x^3-3x^2+1$
②$y=x^3+2x$
この動画を見る
◎次の関数の増減を調べよう。
①$y=2x^3-3x^2+1$
②$y=x^3+2x$
【高校数学】 数Ⅱ－１４９ 接線③
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①2曲線$y=x^2+1、y=-2x^2+4x-3$の共通接線の方程式を求めよう。
この動画を見る
①2曲線$y=x^2+1、y=-2x^2+4x-3$の共通接線の方程式を求めよう。
【高校数学】 数Ⅱ－１４８ 接線②
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①曲線$y=x^3-5x$上の点(1.-4)における接線に垂直な直線の方程式を 求めよう。
②曲線$y=x^3+ax+1$と直線$y=2x-1$が接するとき、aの値を求めよう。
この動画を見る
①曲線$y=x^3-5x$上の点(1.-4)における接線に垂直な直線の方程式を 求めよう。
②曲線$y=x^3+ax+1$と直線$y=2x-1$が接するとき、aの値を求めよう。
【高校数学】 数Ⅱ－１４７ 接線①
【高校数学】 数Ⅱ－１４６ 微分係数と導関数③
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の条件を満たす3次関数$f(x)$を求めよう。
①$x^3$の係数が$1,f(1)=2, f(-1)=-2, f'(-1)=0$
② $f(x) +x f(x) = 4x^3-9x^2+6x+1$
この動画を見る
◎次の条件を満たす3次関数$f(x)$を求めよう。
①$x^3$の係数が$1,f(1)=2, f(-1)=-2, f'(-1)=0$
② $f(x) +x f(x) = 4x^3-9x^2+6x+1$
【高校数学】 数Ⅱ－１４５ 微分係数と導関数②
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$f(x)=3x^2$の$x-2$における微分係数f'(2)を求めよう。
◎次の関数を微分しよう。
②$y=x^3+x^2+x+a$
③$y=-2x^3+7x-1$
④$y=-3$
⑤$y=x^4-3x^2+5x$
⑥$y=\displaystyle \frac{5}{2}x^4-\displaystyle \frac{2}{3}x-3+2$
⑦$y=(3x+5)(２x-1)$
この動画を見る
$f(x)=3x^2$の$x-2$における微分係数f'(2)を求めよう。
◎次の関数を微分しよう。
②$y=x^3+x^2+x+a$
③$y=-2x^3+7x-1$
④$y=-3$
⑤$y=x^4-3x^2+5x$
⑥$y=\displaystyle \frac{5}{2}x^4-\displaystyle \frac{2}{3}x-3+2$
⑦$y=(3x+5)(２x-1)$
【高校数学】 数Ⅱ－１４４ 微分係数と導関数①
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の関数の与えられた範囲における平均へ過率を求めよう。
①$y=x^2(1 \leqq x \leqq 3)$
②$y=2x^2-1(a \leqq x \leqq b)$
◎次の極限を求めよう。
③3$\displaystyle \lim_{ x \to 3 }(x^2-1)$
④$\displaystyle \lim_{ h \to 0 }(3+2h)$
⑤$\displaystyle \lim_{ x \to 2 }(\displaystyle \frac{x+1}{x-1})$
⑥$\displaystyle \lim_{ h \to 0 }(\displaystyle \frac{h^2+3h}{h})$
⑦$\displaystyle \lim_{ x \to 2 }\displaystyle \frac{(x-2)(x^2+x-1)}{(x-2)(x+1)}$
この動画を見る
◎次の関数の与えられた範囲における平均へ過率を求めよう。
①$y=x^2(1 \leqq x \leqq 3)$
②$y=2x^2-1(a \leqq x \leqq b)$
◎次の極限を求めよう。
③3$\displaystyle \lim_{ x \to 3 }(x^2-1)$
④$\displaystyle \lim_{ h \to 0 }(3+2h)$
⑤$\displaystyle \lim_{ x \to 2 }(\displaystyle \frac{x+1}{x-1})$
⑥$\displaystyle \lim_{ h \to 0 }(\displaystyle \frac{h^2+3h}{h})$
⑦$\displaystyle \lim_{ x \to 2 }\displaystyle \frac{(x-2)(x^2+x-1)}{(x-2)(x+1)}$
練習問題29 数検 教採 極限値
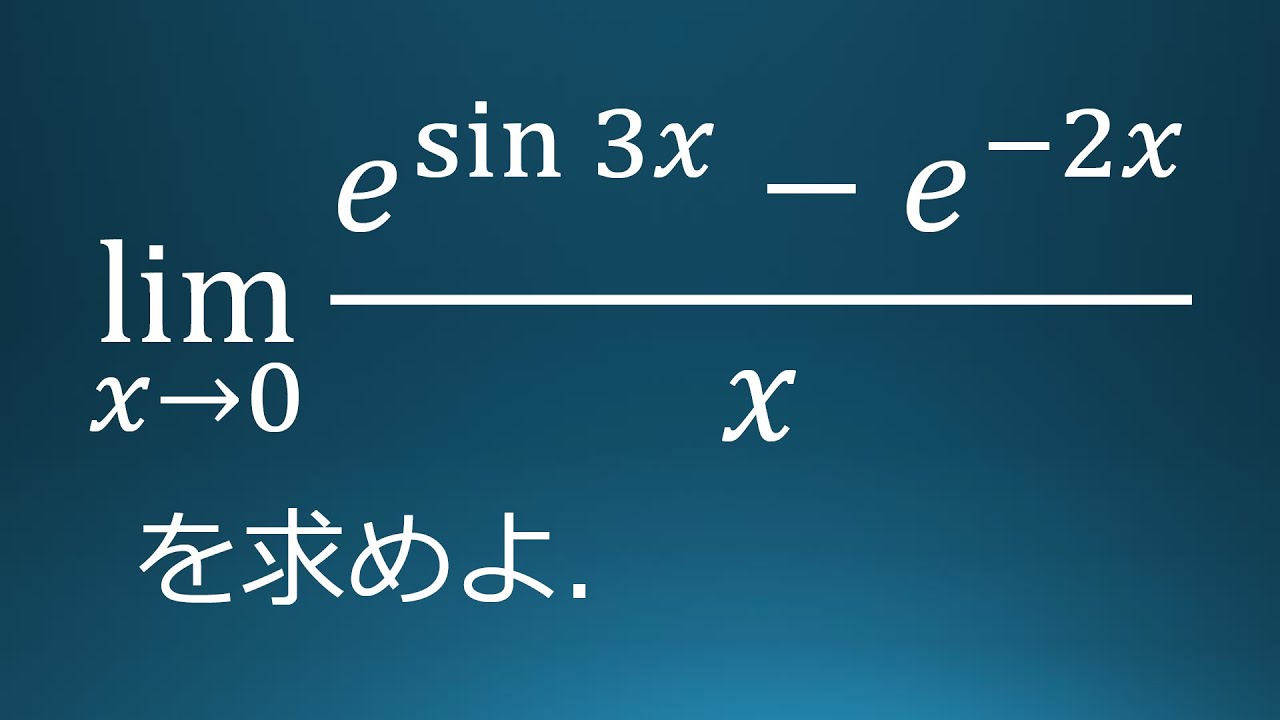
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to 0}\dfrac{e^{\sin 3x}-e^{-2x}}{x}$
を求めよ.
この動画を見る
$\displaystyle \lim_{x\to 0}\dfrac{e^{\sin 3x}-e^{-2x}}{x}$
を求めよ.