微分法と積分法
微分法と積分法
福田の数学〜明治大学2024全学部統一IⅡAB第2問〜高次方程式の解と面積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x$についての関数$f(x), g(x), h(x)$を$f(x) = 4x^4, g(x) = 12x + 8, h(x) = 4x^2+1$により定める。座標平面上で曲線 $y = f(x)$と直線$y=g(x)$は、異なる2点で交わる。それら交点の$x$座標を$a, b$ ($a \lt b$)とする。
(1) $f(x)+h(x) = (\fbox{ ア }x^2+\fbox{ イ })^2, g(x)+h(x) = (\fbox{ ウ }x+\fbox{ エ })^2$である。
(2) $a+b=\fbox{ オ }, b-a=\sqrt{ \fbox{ カ } }$である。
この動画を見る
$x$についての関数$f(x), g(x), h(x)$を$f(x) = 4x^4, g(x) = 12x + 8, h(x) = 4x^2+1$により定める。座標平面上で曲線 $y = f(x)$と直線$y=g(x)$は、異なる2点で交わる。それら交点の$x$座標を$a, b$ ($a \lt b$)とする。
(1) $f(x)+h(x) = (\fbox{ ア }x^2+\fbox{ イ })^2, g(x)+h(x) = (\fbox{ ウ }x+\fbox{ エ })^2$である。
(2) $a+b=\fbox{ オ }, b-a=\sqrt{ \fbox{ カ } }$である。
福田の数学〜明治大学2024全学部統一IⅡAB第2問〜高次方程式の解と面積
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
\fcolorbox{#000}{ #fff }{2}
$
$
xについての関数f(x), g(x), h(x)を
$
$
f(x) = 4x ^ 4 , \quad g(x) = 12x + 8 h(x) = 4x ^ 2 + 1
$
$
により定める。座標平面上で曲線 y = f (x)と直線 y = g(x)は、異なる2点で交わる。それら交点の座標をそれぞれa, b(ただしa < b)とする。
$
$
(1) f(x)+h(x) = (
\fcolorbox{#000}{ #fff }{$ア \ \ $}
x² +
\fcolorbox{#000}{ #fff }{$イ \ \ $}
)², g(x)+h(x) = (
\fcolorbox{#000}{ #fff }{$ウ \ \ $}
x+
\fcolorbox{#000}{ #fff }{$エ \ \ $}
)^2 である。
$
$
(2) a + b =
\fcolorbox{#000}{ #fff }{$オ \ \ $}
b - a = \sqrt{
\fcolorbox{#000}{ #fff }{$カ \ \ $}}
である。
$
$
(3) x = a, \ x = bはx^5 =
\fcolorbox{#000}{ #fff }{$カ \ \ $}
x +
\fcolorbox{#000}{ #fff }{$ク \ \ $}
を満たすので、 b ^ 5 - a ^ 5 =
\fcolorbox{#000}{ #fff }{$ケ \ \ $}
\sqrt{
\fcolorbox{#000}{ #fff }{$コ \ \ $}}
である。
$
$
(4) 座標平面上で曲線y = f(x) と直線y = g(x) で囲まれる図形の面積は
\fcolorbox{#000}{ #fff }{$サシ \ \ \ \ \ $}
\sqrt{\fcolorbox{#000}{ #fff }{$ス \ \ $}}
である。
$
この動画を見る
$
\fcolorbox{#000}{ #fff }{2}
$
$
xについての関数f(x), g(x), h(x)を
$
$
f(x) = 4x ^ 4 , \quad g(x) = 12x + 8 h(x) = 4x ^ 2 + 1
$
$
により定める。座標平面上で曲線 y = f (x)と直線 y = g(x)は、異なる2点で交わる。それら交点の座標をそれぞれa, b(ただしa < b)とする。
$
$
(1) f(x)+h(x) = (
\fcolorbox{#000}{ #fff }{$ア \ \ $}
x² +
\fcolorbox{#000}{ #fff }{$イ \ \ $}
)², g(x)+h(x) = (
\fcolorbox{#000}{ #fff }{$ウ \ \ $}
x+
\fcolorbox{#000}{ #fff }{$エ \ \ $}
)^2 である。
$
$
(2) a + b =
\fcolorbox{#000}{ #fff }{$オ \ \ $}
b - a = \sqrt{
\fcolorbox{#000}{ #fff }{$カ \ \ $}}
である。
$
$
(3) x = a, \ x = bはx^5 =
\fcolorbox{#000}{ #fff }{$カ \ \ $}
x +
\fcolorbox{#000}{ #fff }{$ク \ \ $}
を満たすので、 b ^ 5 - a ^ 5 =
\fcolorbox{#000}{ #fff }{$ケ \ \ $}
\sqrt{
\fcolorbox{#000}{ #fff }{$コ \ \ $}}
である。
$
$
(4) 座標平面上で曲線y = f(x) と直線y = g(x) で囲まれる図形の面積は
\fcolorbox{#000}{ #fff }{$サシ \ \ \ \ \ $}
\sqrt{\fcolorbox{#000}{ #fff }{$ス \ \ $}}
である。
$
#高知工科大学2024#定積分_25#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{3} x|x-2| dx$
出典：2024年 高知工科大学
この動画を見る
$\displaystyle \int_{-1}^{3} x|x-2| dx$
出典：2024年 高知工科大学
#高専#不定積分_16#元高専教員
単元：
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x-1}{\sqrt[ 3 ]{ x }-1} dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x-1}{\sqrt[ 3 ]{ x }-1} dx$
#高知工科大学2024#不定積分_23#元高校教員
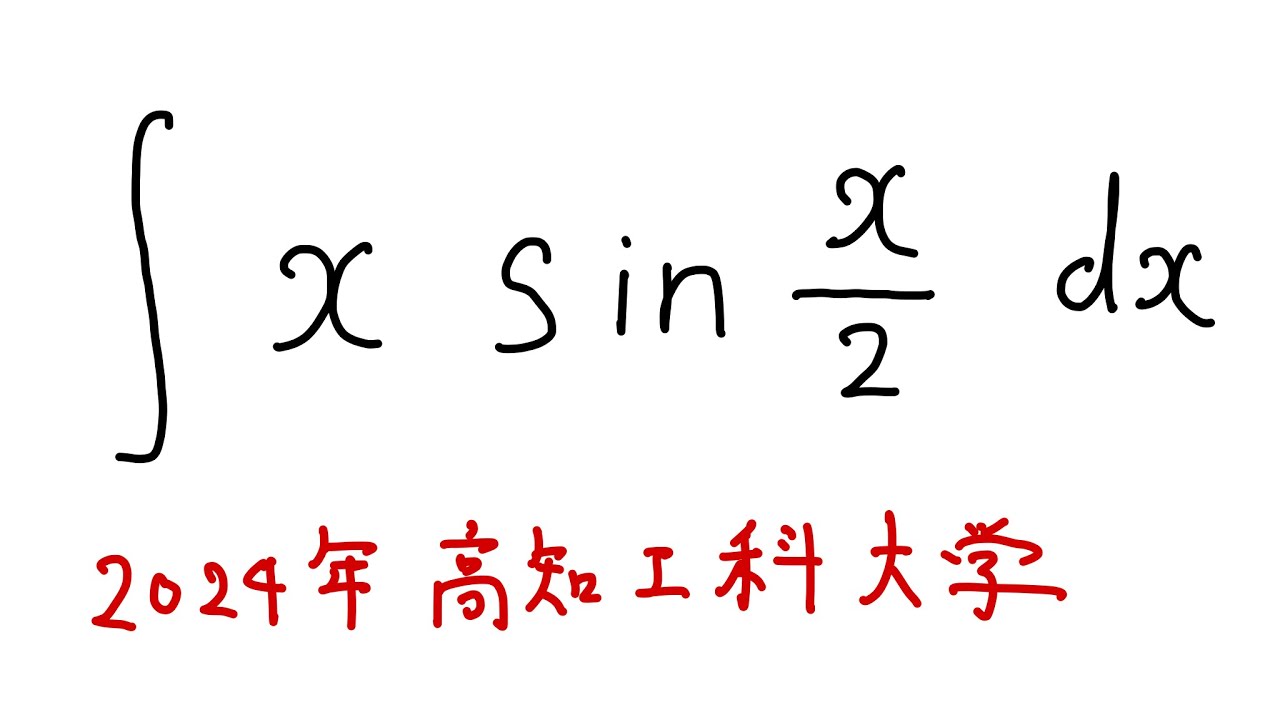
単元：
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int x \sin\displaystyle \frac{x}{2} dx$
出典：2024年高知工科大学
この動画を見る
$\displaystyle \int x \sin\displaystyle \frac{x}{2} dx$
出典：2024年高知工科大学
福田のおもしろ数学238〜4つの放物線で囲まれた図形の面積
#高専#ウォリス積分_15#元高専教員
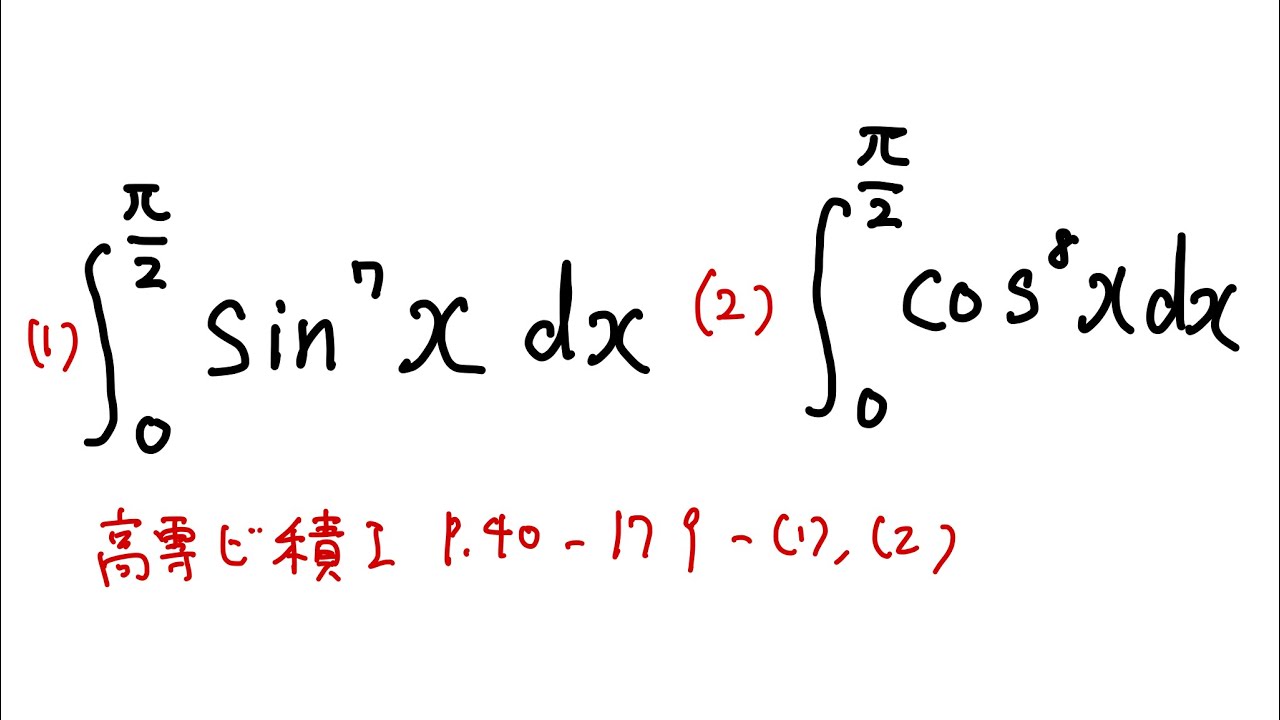
単元：
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
（1）$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7 x$ $dx$
（2）$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^8 x$ $dx$
この動画を見る
（1）$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7 x$ $dx$
（2）$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^8 x$ $dx$
#広島市立大学2024#不定積分_22#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x}{e^{ \frac{x}{2}}} dx$
出典：2024年広島市立大学後期 不定積分問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{e^{ \frac{x}{2}}} dx$
出典：2024年広島市立大学後期 不定積分問題
#高専#不定積分_14#元高専教員
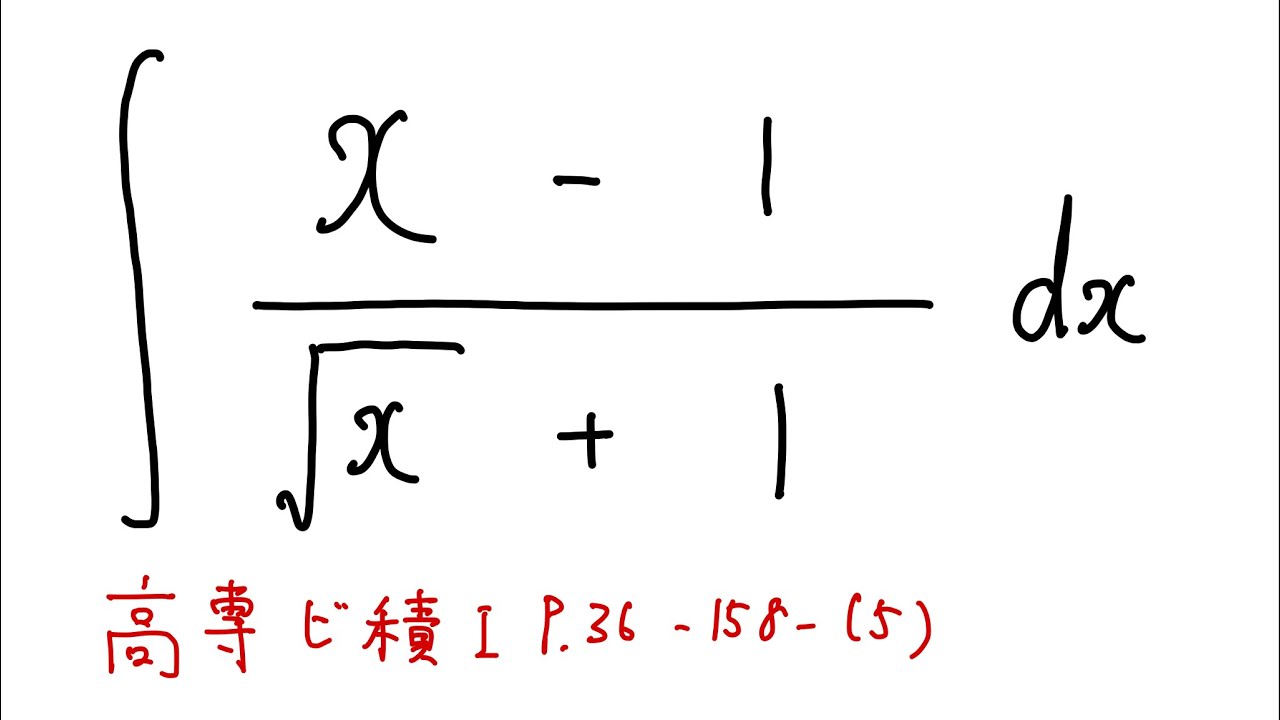
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x-1}{\sqrt{ x }+1}dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x-1}{\sqrt{ x }+1}dx$
大学入試問題#914「コメントむずい」 #学習院大学2023 #積分方程式
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#学習院大学
指導講師：
ますただ
問題文全文(内容文)：
$f(0)=0$
$f'(x)+\displaystyle \int_{0}^{1} f(t) dt=2e^{2x}-e^x$
を満たす関数$f(x)$を求めよ。
出典：2023年学習院大学
この動画を見る
$f(0)=0$
$f'(x)+\displaystyle \int_{0}^{1} f(t) dt=2e^{2x}-e^x$
を満たす関数$f(x)$を求めよ。
出典：2023年学習院大学
福田の数学〜明治大学2024全学部統一IⅡAB第1問(1)〜接線と法線の方程式
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面上の放物線 $y=2x^2-1$ を考える。 $t$ を $0$ でない定数とするとき、放物線上の点 $\mathrm{P}(t,2t^2-1)$ における接線 $l$ の方程式は
$y=\fbox{ア}x $$- \fbox{イ}t^2 $$- \fbox{ウ}$
である。点 $\mathrm{P}$ を通りこの接線 $l$ に直交する直線を点 $\mathrm{P}$ における法線と呼ぶことにすると、この法線の方程式は
$y=\fbox{エ}x $$+ \fbox{オ}t^2 $$- \frac{\fbox{カ}}{\fbox{キ}}$ である。
ア、エの解答群は動画内参照。
この動画を見る
座標平面上の放物線 $y=2x^2-1$ を考える。 $t$ を $0$ でない定数とするとき、放物線上の点 $\mathrm{P}(t,2t^2-1)$ における接線 $l$ の方程式は
$y=\fbox{ア}x $$- \fbox{イ}t^2 $$- \fbox{ウ}$
である。点 $\mathrm{P}$ を通りこの接線 $l$ に直交する直線を点 $\mathrm{P}$ における法線と呼ぶことにすると、この法線の方程式は
$y=\fbox{エ}x $$+ \fbox{オ}t^2 $$- \frac{\fbox{カ}}{\fbox{キ}}$ である。
ア、エの解答群は動画内参照。
#高専数学#不定積分_13#元高専教員
単元：
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
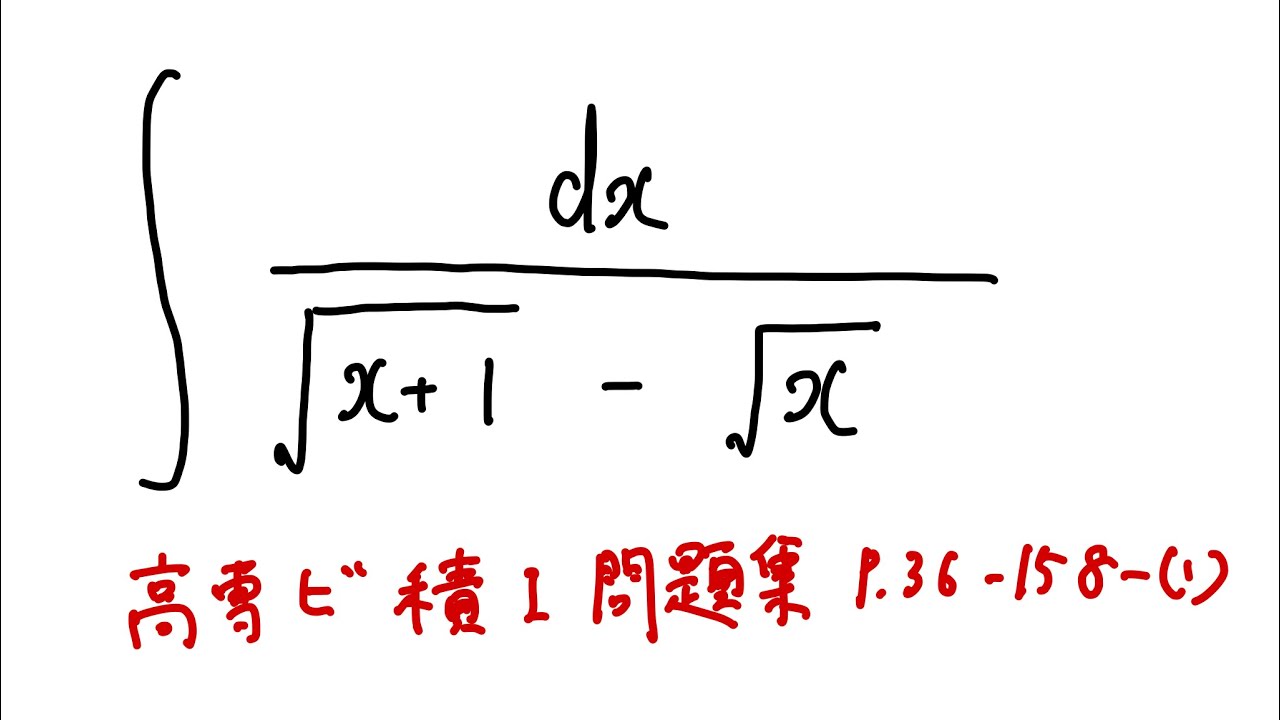
$\displaystyle \int \displaystyle \frac{dx}{\sqrt{ x+1 }-\sqrt{ x }}$
出典：高専数学 問題集
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{\sqrt{ x+1 }-\sqrt{ x }}$
出典：高専数学 問題集
#宮崎大学2024#不定積分_20#元高校教員
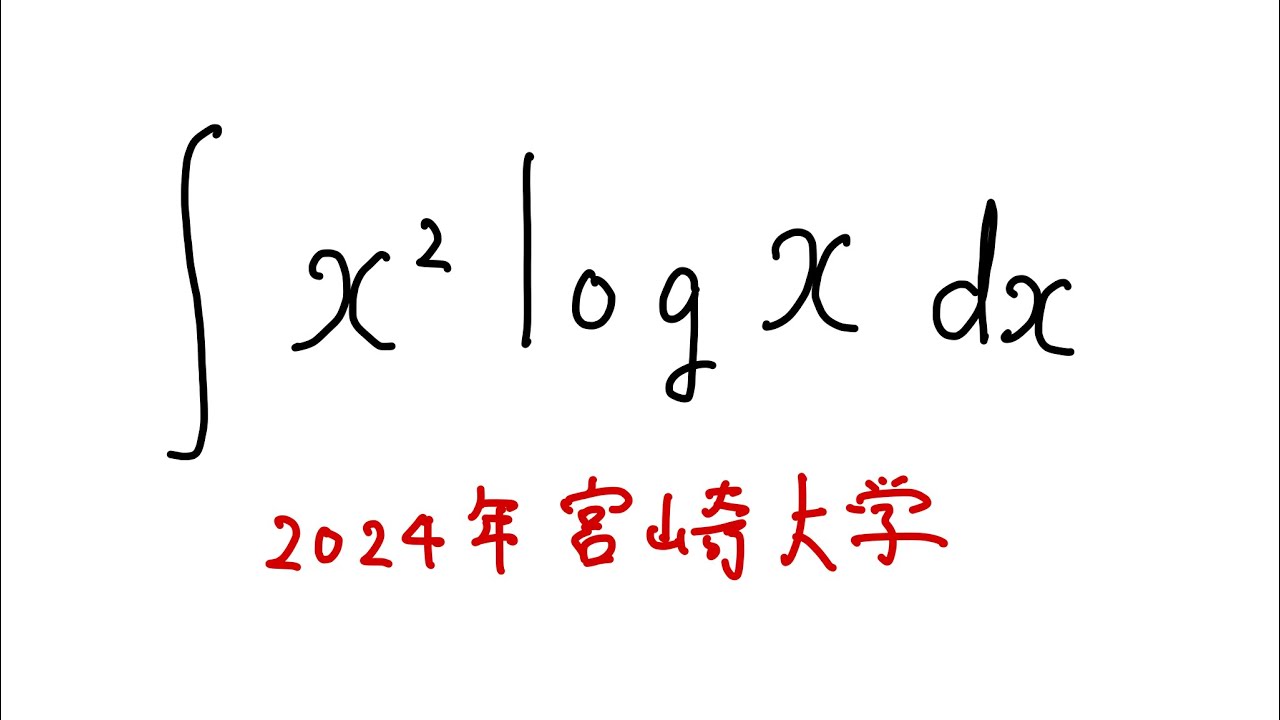
単元：
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int x^2log$ $x$ $dx$
出典：2024年 宮崎大学
この動画を見る
$\displaystyle \int x^2log$ $x$ $dx$
出典：2024年 宮崎大学
大学入試問題#913「作成者サイコ−！」 #広島市立大学後期2024
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{2}^{8} \displaystyle \frac{1}{x(x+1)}log \displaystyle \frac{x}{x+1} dx$
出典：2024年 広島市立大学後期試験
この動画を見る
$\displaystyle \int_{2}^{8} \displaystyle \frac{1}{x(x+1)}log \displaystyle \frac{x}{x+1} dx$
出典：2024年 広島市立大学後期試験
#宮崎大学2024#不定積分_19#元高校教員
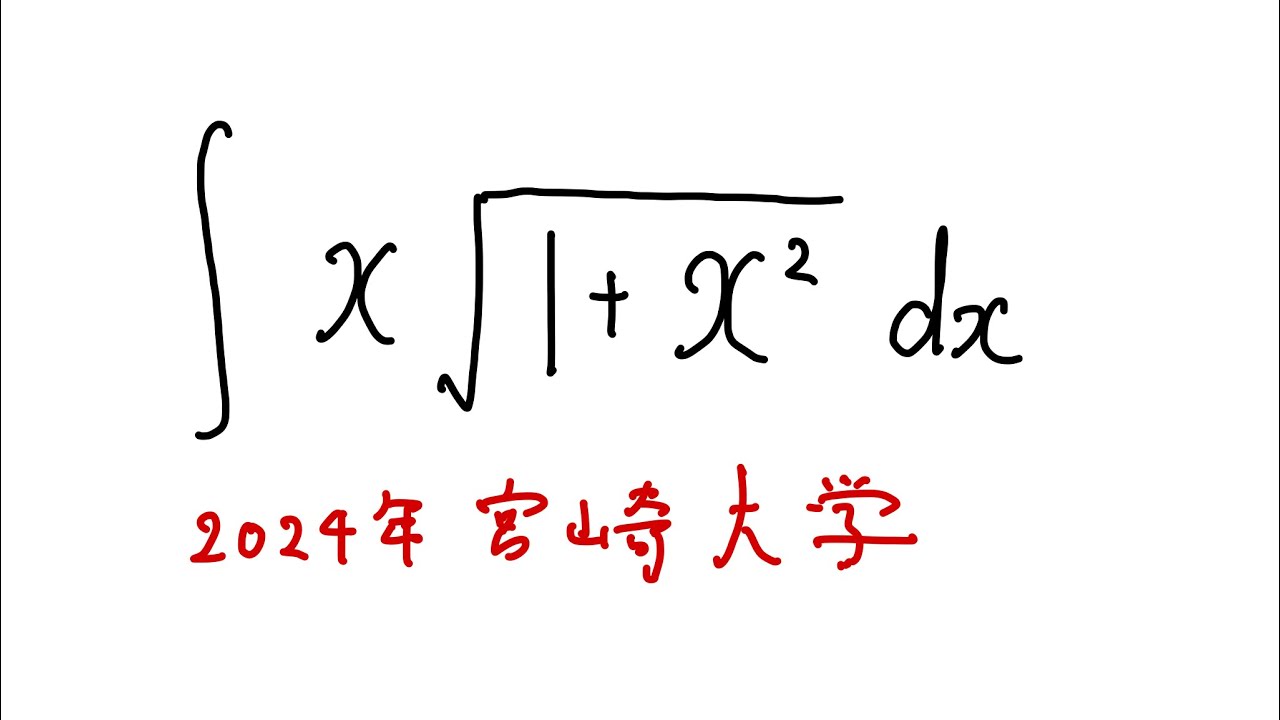
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#宮崎大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int x \sqrt{ 1+x^2 }dx$
出典：2024年宮崎大学
この動画を見る
$\displaystyle \int x \sqrt{ 1+x^2 }dx$
出典：2024年宮崎大学
#名古屋工業大学2024#不定積分_18#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#名古屋大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int\sqrt{ 2 }$ $logx$ $dx$
出典：2024年 名古屋工業大学
この動画を見る
$\displaystyle \int\sqrt{ 2 }$ $logx$ $dx$
出典：2024年 名古屋工業大学
#宮崎大学2024#定積分_17#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#宮崎大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{3}} \cos^2\displaystyle \frac{x}{4} dx$
出典：2024年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}} \cos^2\displaystyle \frac{x}{4} dx$
出典：2024年宮崎大学
#前橋工科大学2017#定積分_16#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi} t\sin^2t$ $dt$
出典：2017年前橋工科大学
この動画を見る
$\displaystyle \int_{0}^{2\pi} t\sin^2t$ $dt$
出典：2017年前橋工科大学
#名古屋工業大学2020#定積分_15#元高校教員
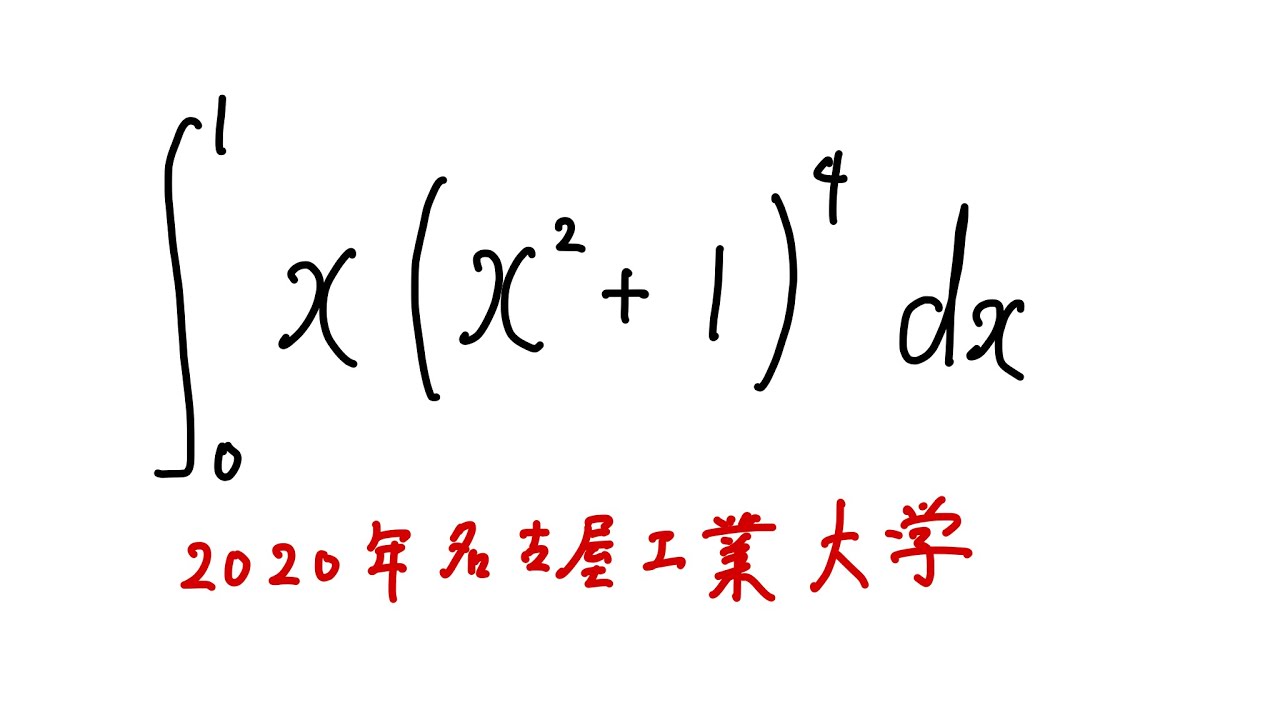
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x(x^2+1)^4 dx$
出典：2020年名古屋工業大学
この動画を見る
$\displaystyle \int_{0}^{1} x(x^2+1)^4 dx$
出典：2020年名古屋工業大学
#前橋工科大学2021#定積分_14#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{13} \displaystyle \frac{dx}{\sqrt[ 3 ]{ (2x+1)^5 }}$
出典：2021年前橋工科大学
この動画を見る
$\displaystyle \int_{0}^{13} \displaystyle \frac{dx}{\sqrt[ 3 ]{ (2x+1)^5 }}$
出典：2021年前橋工科大学
大学入試問題#910「いやーいかにもミスりそう」 #琉球大学2021
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#琉球大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} |3\sin x+\cos x| dx$
出典：2021年琉球大学後期
この動画を見る
$\displaystyle \int_{0}^{\pi} |3\sin x+\cos x| dx$
出典：2021年琉球大学後期
#前橋工科大学2024#定積分_13#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{1}{2}(1-\cos x)^2 dx$
出典：2024年前橋工科大学
この動画を見る
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{1}{2}(1-\cos x)^2 dx$
出典：2024年前橋工科大学
#群馬大学推薦2023#定積分_12#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#群馬大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{\pi}{2n}\sin\displaystyle \frac{k \pi }{2n}$
出典：2023年群馬大学推薦
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{\pi}{2n}\sin\displaystyle \frac{k \pi }{2n}$
出典：2023年群馬大学推薦
#茨城大学2024#定積分_11#元高校教員
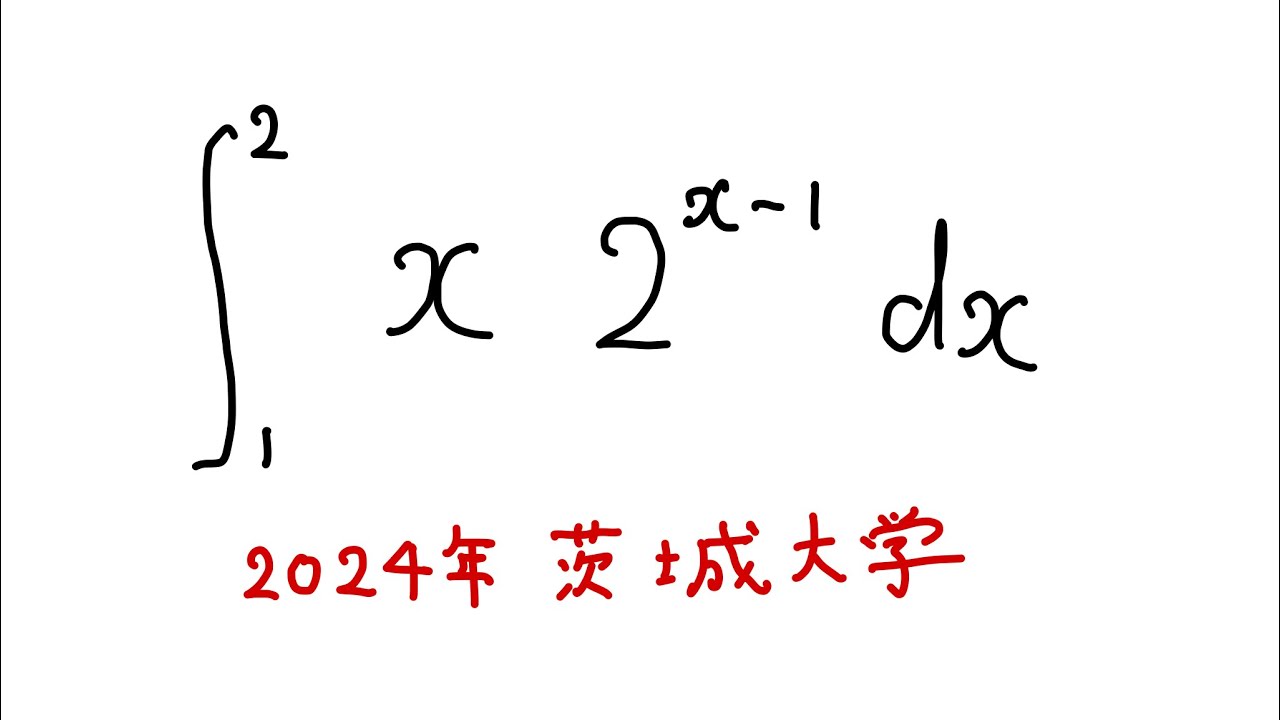
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} x 2^{x-1}$ $dx$
出典：2024年茨城大学
この動画を見る
$\displaystyle \int_{1}^{2} x 2^{x-1}$ $dx$
出典：2024年茨城大学
#茨城大学2022#極限_10#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to -\infty } \displaystyle \frac{4^{x+2}+2^{x-2}}{4^x-2^x}$
出典：2022年茨城大学
この動画を見る
$\displaystyle \lim_{ x \to -\infty } \displaystyle \frac{4^{x+2}+2^{x-2}}{4^x-2^x}$
出典：2022年茨城大学
大学入試問題#909「基本に忠実に」 前橋工科大学(2023)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\sqrt{ 3 }} (x^7-3x^3)e-\displaystyle \frac{x^4}{4}$ $dx$
出典：2023年前橋工科大学
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ 3 }} (x^7-3x^3)e-\displaystyle \frac{x^4}{4}$ $dx$
出典：2023年前橋工科大学
#会津大学2023#定積分_9#元高校教員
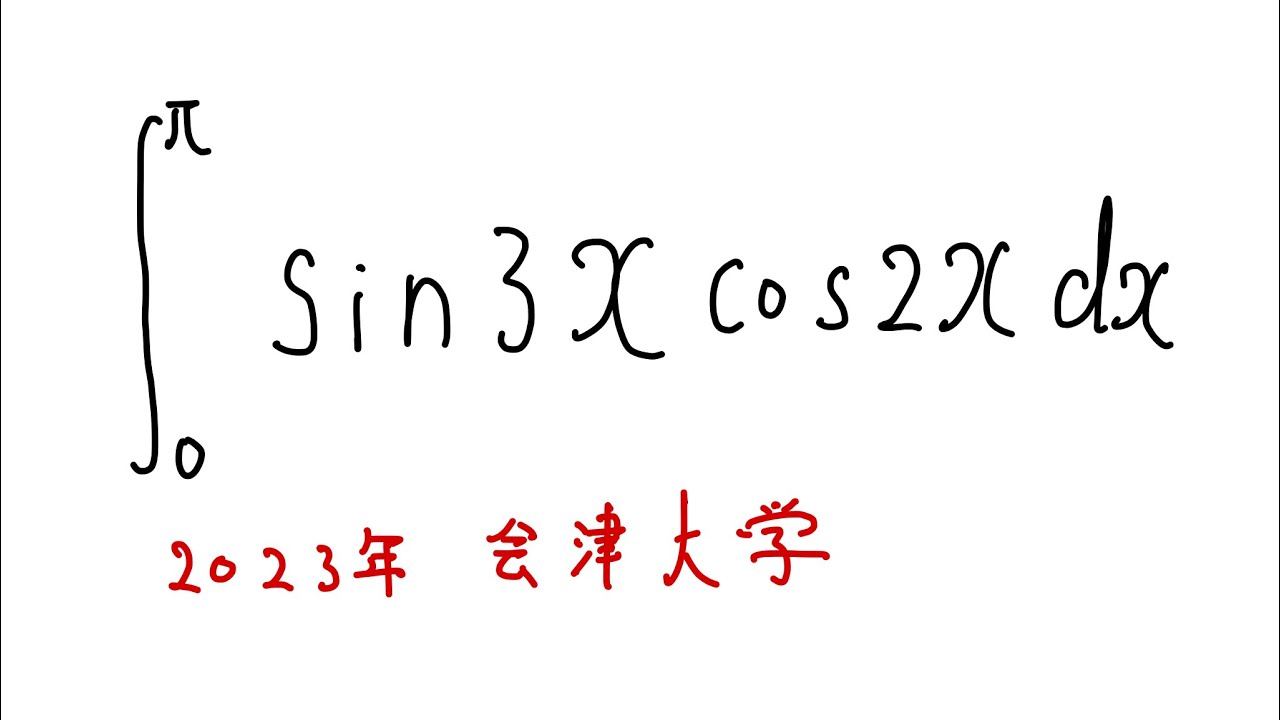
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} \sin3x\cos2x$ $dx$
出典：2023年会津大学
この動画を見る
$\displaystyle \int_{0}^{\pi} \sin3x\cos2x$ $dx$
出典：2023年会津大学
#茨城大学2024#定積分_8#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos\theta\sin 2 \theta d \theta$
出典：2024年茨城大学後期
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos\theta\sin 2 \theta d \theta$
出典：2024年茨城大学後期
福田のおもしろ数学239〜定積分と不等式の関係
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$k>0$ のとき、
$\displaystyle
\frac{1}{2(k+1)}<\int^{1}_{0}\frac{1-x}{k+x}dx<\frac{1}{2k}
$
を示して下さい。
この動画を見る
$k>0$ のとき、
$\displaystyle
\frac{1}{2(k+1)}<\int^{1}_{0}\frac{1-x}{k+x}dx<\frac{1}{2k}
$
を示して下さい。
大学入試問題#908「正確に対応するだけ」 #信州大学理学部(2024) #積分方程式
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
次の等式を満たす関数$f(x)$を求めよ
$f(x)=x+\displaystyle \int_{0}^{\pi} f(t) \cos(x+t) dt$
出典：2024年信州大学理学部
この動画を見る
次の等式を満たす関数$f(x)$を求めよ
$f(x)=x+\displaystyle \int_{0}^{\pi} f(t) \cos(x+t) dt$
出典：2024年信州大学理学部